13.2 与三角形有关的线段课件(共20张PPT)人教版八年级数学上册
文档属性
| 名称 | 13.2 与三角形有关的线段课件(共20张PPT)人教版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 657.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 14:40:34 | ||
图片预览








文档简介
(共20张PPT)
第十三章 三角形
13.2 与三角形有关的线段
三角形的边是构成三角形的元素,本节我们研究三角形三边之间的关系,并认识与三角形有关的三种重要线段。
新课导入
学习目标
1.掌握三角形三边之间的关系.
2.会利用三边之间的关系判断能否组成三角形.
3.了解三角形的稳定性,会解释生活中与三角形稳定性有关的现象.
4.理解三角形的中线、角平分线和高的定义,并能在具体三角形中画出三角形的高、中线和角平分线.
13.2.1 三角形的边
探究
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择 各条线路的长有什么关系 这说明三角形的边之间有什么关系?能证明你的结论吗
A
B
C
在从点B到点C的线路中,由点B先到点A再到点C的线路,比由点B直接到点C的线路长,即BA+AC>BC,这利用了在小学我们学过的“三角形两边的和大于第三边”的结论.下面对这个结论进行证明.
对于任意一个△ABC,如果把其中任意两个顶点(例如B,C)看成定点,由“两点之间,线段最短”,可得
AB+AC>BC ①
同理有
AC+BC>AB ②
AB+BC>AC ③
这样,我们就证明了,三角形两边的和大于第三边.
进一步,由不等式②③,移项可得
BC>AB-AC,
BC>AC-AB.
这就是说,三角形两边的差小于第三边.
思考
上面的结论表明了三角形三边之间的关系,反过来,对于三条线段,当它们满足什么条件时,这三条线段能组成三角形
一般地,如果三条线段中任意两条线段的和大于第三条线段,那么这三条线段能组成三角形;如果三条线段中有两条线段的和小于或等于第三条线段,那么这三条线段不能组成三角形.
典例精析
例 用一条长为18cm的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm,则
x+2x+2x=18.
解得 x=3.6.
所以,三角形三边的长分别为3.6cm,7.2cm,7.2cm
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
①如果4cm长的边为底边,设腰长为x cm,则
4+2x=18.
解得x=7.
②如果4cm长的边为腰,设底边长为y cm,则
2×4+y=18.
解得 y=10
因为4+4<10,不符合“三角形两边的和大于第三边”,所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边长是4cm的等腰三角形.
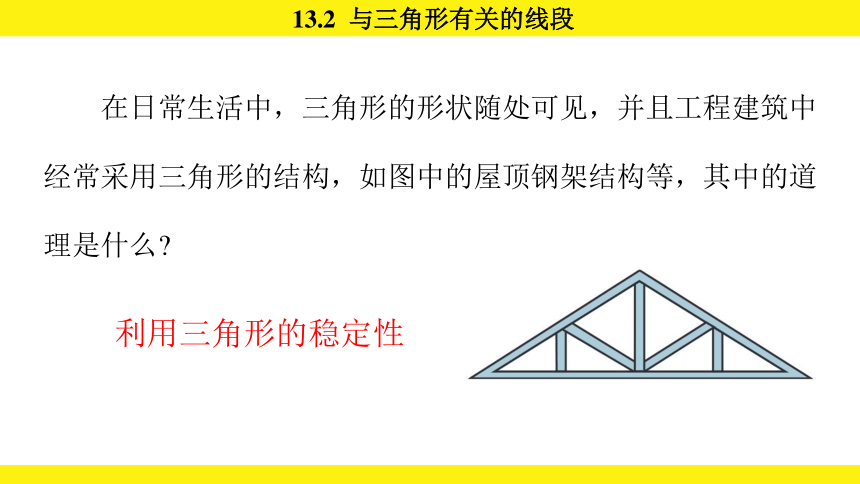
在日常生活中,三角形的形状随处可见,并且工程建筑中经常采用三角形的结构,如图中的屋顶钢架结构等,其中的道理是什么
利用三角形的稳定性
探究
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
形状不会改变.
可以发现,三角形木架的形状不会改变,这就是说,三角形是具有稳定性的图形.
三角形的稳定性有着广泛的应用,下图表示其中一些例子,你能再举些例子吗
钢架桥
当堂练习
1.下列长度的三条线段能否组成三角形?为什么?
(1)3, 4, 8; (2)5, 6, 11; (3)5, 6, 10
解:(1)不能.
因为3+4<8,所以长度为3,4,8的三条线段不能组成三角形.
(2)不能.
因为5+6=11,所以长度为5,6,11的三条线段不能组成三角形.
(3)能.
因为5+6>10,所以长度为5,6,10的三条线段能组成三角形.
当堂练习
2.一根4 dm长的木条和两根1 dm长的木条,能否组成一个等腰三角形?
两根4 dm长的木条和一根1 dm长的木条呢
不能.
能.
13.2.2 三角形的中线、角平分线、高
与三角形有关的线段,除了三条边,还有三种重要的线段:三角形的中线、角平分线、高.
如图 (1),连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫作△ABC的边BC上的中线.
一个三角形有三条中线,这三条中线相交于一点,如图(2). 三角形三条中线的交点叫作三角形的重心.
如图(1),画△ABC的∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫作△ABC的角平分线. 三角形的三条角平分线相交于一点如图(2).
A
F
E
B
D
C
(1)
(2)
如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫作△ABC的边BC上的高线. 三角形的高线简称三角形的高.
探究
分别画出锐角三角形、直角三角形、钝角三角形的三条高,你有什么发现
锐角三角形的三条高都在三角形的内部 (图(1));直角三角形有两条高恰好是它的两条直角边(图(2));钝角三角形有两条高在三角形的外部,两个垂足落在边的延长线上(图(3)).
A
F
E
B
D
C
(1)
(2)
(3)
当堂练习
1. 如图,过△ABC的顶点C分别画出它的中线、角平分线和高.
当堂练习
2.填空:
(1)如下图(1),AD,BE,CF是△ABC的三条中线,则BD =________,AE = ______,AB = 2 ___________,
(2)如下图(2),AD,BE,CF是△ABC的三条角平分线,则∠1 =____ ,∠3 = ________,∠ACB = 2 ______________.
DC
AC
AF(或BF)
∠2
∠ABC
∠4(或∠ACF)
谢谢观看
第十三章 三角形
13.2 与三角形有关的线段
三角形的边是构成三角形的元素,本节我们研究三角形三边之间的关系,并认识与三角形有关的三种重要线段。
新课导入
学习目标
1.掌握三角形三边之间的关系.
2.会利用三边之间的关系判断能否组成三角形.
3.了解三角形的稳定性,会解释生活中与三角形稳定性有关的现象.
4.理解三角形的中线、角平分线和高的定义,并能在具体三角形中画出三角形的高、中线和角平分线.
13.2.1 三角形的边
探究
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择 各条线路的长有什么关系 这说明三角形的边之间有什么关系?能证明你的结论吗
A
B
C
在从点B到点C的线路中,由点B先到点A再到点C的线路,比由点B直接到点C的线路长,即BA+AC>BC,这利用了在小学我们学过的“三角形两边的和大于第三边”的结论.下面对这个结论进行证明.
对于任意一个△ABC,如果把其中任意两个顶点(例如B,C)看成定点,由“两点之间,线段最短”,可得
AB+AC>BC ①
同理有
AC+BC>AB ②
AB+BC>AC ③
这样,我们就证明了,三角形两边的和大于第三边.
进一步,由不等式②③,移项可得
BC>AB-AC,
BC>AC-AB.
这就是说,三角形两边的差小于第三边.
思考
上面的结论表明了三角形三边之间的关系,反过来,对于三条线段,当它们满足什么条件时,这三条线段能组成三角形
一般地,如果三条线段中任意两条线段的和大于第三条线段,那么这三条线段能组成三角形;如果三条线段中有两条线段的和小于或等于第三条线段,那么这三条线段不能组成三角形.
典例精析
例 用一条长为18cm的细绳围成一个等腰三角形.
(1) 如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm,则
x+2x+2x=18.
解得 x=3.6.
所以,三角形三边的长分别为3.6cm,7.2cm,7.2cm
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
①如果4cm长的边为底边,设腰长为x cm,则
4+2x=18.
解得x=7.
②如果4cm长的边为腰,设底边长为y cm,则
2×4+y=18.
解得 y=10
因为4+4<10,不符合“三角形两边的和大于第三边”,所以不能围成腰长是4cm的等腰三角形.
由以上讨论可知,可以围成底边长是4cm的等腰三角形.
在日常生活中,三角形的形状随处可见,并且工程建筑中经常采用三角形的结构,如图中的屋顶钢架结构等,其中的道理是什么
利用三角形的稳定性
探究
如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
形状不会改变.
可以发现,三角形木架的形状不会改变,这就是说,三角形是具有稳定性的图形.
三角形的稳定性有着广泛的应用,下图表示其中一些例子,你能再举些例子吗
钢架桥
当堂练习
1.下列长度的三条线段能否组成三角形?为什么?
(1)3, 4, 8; (2)5, 6, 11; (3)5, 6, 10
解:(1)不能.
因为3+4<8,所以长度为3,4,8的三条线段不能组成三角形.
(2)不能.
因为5+6=11,所以长度为5,6,11的三条线段不能组成三角形.
(3)能.
因为5+6>10,所以长度为5,6,10的三条线段能组成三角形.
当堂练习
2.一根4 dm长的木条和两根1 dm长的木条,能否组成一个等腰三角形?
两根4 dm长的木条和一根1 dm长的木条呢
不能.
能.
13.2.2 三角形的中线、角平分线、高
与三角形有关的线段,除了三条边,还有三种重要的线段:三角形的中线、角平分线、高.
如图 (1),连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫作△ABC的边BC上的中线.
一个三角形有三条中线,这三条中线相交于一点,如图(2). 三角形三条中线的交点叫作三角形的重心.
如图(1),画△ABC的∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫作△ABC的角平分线. 三角形的三条角平分线相交于一点如图(2).
A
F
E
B
D
C
(1)
(2)
如图,从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫作△ABC的边BC上的高线. 三角形的高线简称三角形的高.
探究
分别画出锐角三角形、直角三角形、钝角三角形的三条高,你有什么发现
锐角三角形的三条高都在三角形的内部 (图(1));直角三角形有两条高恰好是它的两条直角边(图(2));钝角三角形有两条高在三角形的外部,两个垂足落在边的延长线上(图(3)).
A
F
E
B
D
C
(1)
(2)
(3)
当堂练习
1. 如图,过△ABC的顶点C分别画出它的中线、角平分线和高.
当堂练习
2.填空:
(1)如下图(1),AD,BE,CF是△ABC的三条中线,则BD =________,AE = ______,AB = 2 ___________,
(2)如下图(2),AD,BE,CF是△ABC的三条角平分线,则∠1 =____ ,∠3 = ________,∠ACB = 2 ______________.
DC
AC
AF(或BF)
∠2
∠ABC
∠4(或∠ACF)
谢谢观看
同课章节目录
