《高考快车道》2026版高三一轮总复习数学(基础版)14 第二章 思维进阶1 函数性质的综合应用 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)14 第二章 思维进阶1 函数性质的综合应用 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:46 | ||
图片预览





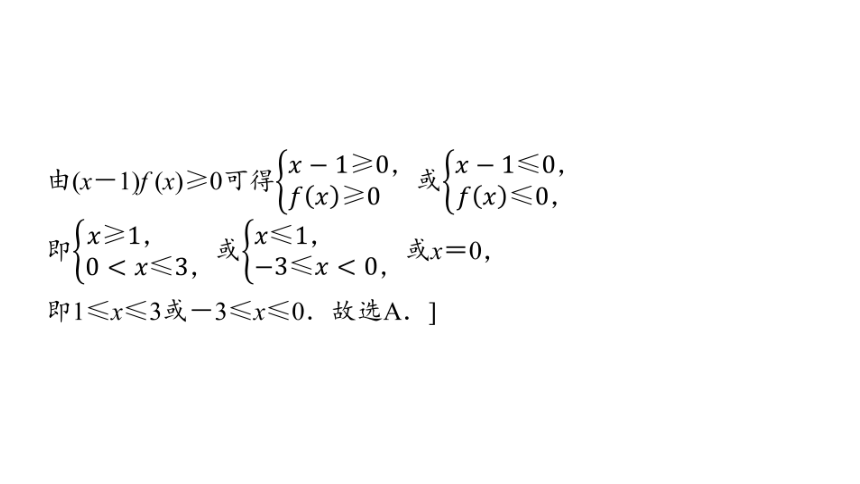






文档简介
(共41张PPT)
第二章 函数
思维进阶1 函数性质的综合应用
函数性质的综合应用是历年高考的一个热点内容,经常以客观题出现,通过分析函数的性质特点,结合图象研究函数的性质,往往多种性质结合在一起进行考查.
题型一 函数的奇偶性与单调性
[典例1] (1)设f (x)是R上的偶函数,且在(0,+∞)上单调递减,若x1>0且x1+x2<0,则( )
A.f (x1)>f (x2)
B.f (x1)=f (x2)
C.f (x1)D.f (x1)与f (x2)的大小关系不确定
√
(2)(2024·曲靖麒麟区三模)若定义在R上的函数满足f (x-2)=
-f (2-x),且在(-∞,0)单调递减,f (3)=0,则满足(x-1)f (x)≥0的x的取值范围是( )
A.[-3,0]∪[1,3]
B.(-∞,-3]∪{0}∪[1,3]
C.[-3,0)∪[1,3]
D.[1,+∞)
√
(1)A (2)A [(1)由x1>0,x1+x2<0,得0+∞)上单调递减,∴f (x1)>f (-x2),f (x)是偶函数,f (-x2)=f (x2),
∴f (x1)>f (x2).
(2)因为定义在R上的函数满足f (x-2)=-f (2-x),
所以f (x)为奇函数,
因为f (x)在(-∞,0)单调递减,f (3)=0,
所以f (x)在(0,+∞)上单调递减,且f (-3)=-f (3)=0,f (0)=0,
由(x-1)f (x)≥0可得或
即或或x=0,
即1≤x≤3或-3≤x≤0.故选A.]
反思领悟 奇偶性与单调性综合的两种题型及解法
(1)比较大小问题,一般解法是先利用奇偶性,将不在同一单调区间上的两个或多个自变量的函数值,转化为同一单调区间上的自变量的函数值,然后利用单调性比较大小.
(2)抽象不等式问题,解题步骤是:
①将所给的不等式转化为两个函数值的大小关系;
②利用奇偶性得出区间上的单调性,再利用单调性“脱去”函数的符号“f ”,转化为解不等式(组)的问题.
题型二 函数的奇偶性与周期性
[典例2] 已知定义在R上的奇函数f (x)满足f (x+2)=-f (x),当x∈[0,1]时,f (x)单调递增,则( )
A.f (6)B.f (6)C.f (-7)D.f √
B [∵f (x+2)=-f (x),∴f (x+4)=f ((x+2)+2)=-f (x+2)=
f (x),∴函数f (x)是周期为4的周期函数,
∴f (6)=f (2)=-f (0)=f (0),
f (-7)=f (1),f =f =-f =f ,
又当x∈[0,1]时f (x)单调递增,
∴f (0)即f (6)反思领悟 本题解题关键是利用奇偶性和周期性将f (6),f (-7),
f 中的6,-7,转化到单调区间[0,1]内再比较大小.
题型三 函数性质的综合应用
[典例3] 已知定义在R上的函数f (x)满足f (x+6)=f (x),且y=f (x+3)为偶函数.若f (x)在(0,3)上单调递减,则下列结论正确的是( )
A.f (10)B.f ()C.f (ln 2)D.f (ln 2)√
A [∵f (x+6)=f (x),∴f (x)的周期为6.
又∵y=f (x+3)为偶函数,∴f (x+3)=f (-x+3),∴f (10)=f (4+6)=f (4)=f (1+3)=f (-1+3)=f (2).
∵1<<2,0∴0又∵f (x)在(0,3)上单调递减,∴f (2)故选A.]
反思领悟 对于函数性质结合的题目,函数的周期性有时需要通过函数的奇偶性得到,函数的奇偶性体现的是一种对称关系,而函数的单调性体现的是函数值随自变量变化而变化的规律.因此在解题时,往往需要借助函数的奇偶性和周期性来确定另一区间上的单调性,即实现区间的转换,再利用单调性解决相关问题.
【教用·备选题】
1.(2024·辽宁六校联考)若定义在R上的奇函数f (x)满足f (2-x)=
f (x),在区间(0,1)上,有(x1-x2)[f (x1)-f (x2)]>0,则下列说法正确的是( )
A.函数f (x)的图象关于点(1,0)成中心对称
B.函数f (x)的图象关于直线x=2成轴对称
C.在区间(2,3)上,f (x)单调递减
D.f >f
√
C [f (4-x)=f (2-(x-2))=f (x-2)=-f (2-x)=-f (x),
即f (4-x)+f (x)=0,故f (x)的图象关于点(2,0)成中心对称,B错误;
∵f (2-x)=f (x),则f (x)的图象关于直线x=1成轴对称,A错误;
根据题意可得,f (x)在(0,1)上单调递增,
∵f (x)的图象关于直线x=1成轴对称,关于点(2,0)成中心对称,则f (x)在(2,3)上单调递减,C正确;
又∵f (x)=f (2-x)=-f (x-2),则f (x+2)=-f (x),
∴f (x+4)=-f (x+2)=f (x),可知f (x)的周期为4,
则f =f故选C.]
2.(2022·全国乙卷)已知函数f (x),g(x)的定义域均为R,且f (x)+g(2-x)=5,g(x)-f (x-4)=7.若y=g(x)的图象关于直线x=2对称,g(2)=4,则=( )
A.-21 B.-22
C.-23 D.-24
√
D [因为y=g(x)的图象关于直线x=2对称,所以g(2-x)=g(x+2),因为g(x)-f (x-4)=7,所以g(x+2)-f (x-2)=7,
即g(x+2)=7+f (x-2),
因为f (x)+g(2-x)=5,所以f (x)+g(x+2)=5,
代入得f (x)+[7+f (x-2)]=5,即f (x)+f (x-2)=-2,
所以f (3)+f (5)+…+f (21)=(-2)×5=-10,
f (4)+f (6)+…+f (22)=(-2)×5=-10.
因为f (x)+g(2-x)=5,所以f (0)+g(2)=5,
即f (0)=1,所以f (2)=-2-f (0)=-3.
因为g(x)-f (x-4)=7,所以g(x+4)-f (x)=7,又因为f (x)+g(2-x)=5,联立得,g(2-x)+g(x+4)=12,
所以y=g(x)的图象关于点(3,6)中心对称,因为函数g(x)的定义域为R,所以g(3)=6,因为f (x)+g(x+2)=5,
所以f (1)=5-g(3)=-1.
所以=f (1)+f (2)+[f (3)+f (5)+…+f (21)]+[f (4)+
f (6)+…+f (22)]=-1-3-10-10=-24.故选D.]
3.(多选)(2024·浙江大学附属中学期中)已知f (x)是定义在R上的奇函数,且y=f (x+1)为偶函数,当x∈(0,1]时,f (x)=-x2,下列结论正确的有( )
A.函数f (x)的周期是4
B.直线x=2 023是函数f (x)图象的一条对称轴
C.f (x)在[2 022,2 023]上单调递减
D.f (2 022)+f (2 023)=1
√
√
√
ABD [对于A,因为函数f (x+1)为偶函数,所以f (x+1)=f (-x+1),即f (x)的图象关于直线x=1对称,因为f (x)为奇函数,所以
f (-x)=-f (x),则f (x+2)=f (-(x+1)+1)=f (-x)=-f (x),
所以f (x+4)=-f (x+2)=f (x),所以f (x)是周期为4的函数,故A正确;
因为f (x)的图象关于直线x=1对称,且为奇函数,所以f (x)的图象关于直线x=-1对称,又f (x)是周期为4的函数,所以f (x)的图象关于直线x=3对称,因为2 023=505×4+3,
所以直线x=2 023是函数f (x)图象的一条对称轴,故B正确;
由f (x)是定义在R上的奇函数,所以f (0)=0,
当x∈(0,1]时,f (x)=-x2,可得当x∈[0,1]时,f (x)=-x2,
令x∈[2,3],则x-2∈[0,1],
所以f (x)=-f (x-2)=(x-2)2,此时f (x)单调递增,
因为2 022=505×4+2,
所以f (x)在[2 022,2 023]上的单调性相当于f (x)在[2,3]上的单调性,故此时单调递增,故C错误;
f (2 022)=f (2)=0,f (2 023)=f (3)=1,
所以f (2 022)+f (2 023)=1,故D正确.故选ABD.]
4.(2024·四川眉山仁寿县期中)定义在R上的函数f (x)满足f (x+y)=f (x)+f (y),f (1)=4.
(1)求f (0)的值;
(2)判断函数f (x)的奇偶性,并证明你的结论;
(3)若函数f (x)在[0,+∞)上单调递增,求不等式f (2x+3)-f (x)<8的解集.
[解] (1)令x=y=0,得f (0)=f (0)+f (0),解得f (0)=0.
(2)因为函数f (x)的定义域为R,令y=-x,
则f (x-x)=f (x)+f (-x),
∴f (x)+f (-x)=0,∴f (-x)=-f (x),
∴函数f (x)为奇函数.
(3)∵f (1)=4,令x=y=1,得f (2)=f (1)+f (1)=8,
∵f (2x+3)-f (x)<8,∴f (2x+3)-f (x)<f (2),
∵f (x+y)=f (x)+f (y),
∴f (2x+3)-f (x)=f (2x+3)+f (-x)=f (x+3),∴f (x+3)<f (2).
∵函数f (x)在[0,+∞)上单调递增,且函数f (x)为奇函数,
∴函数f (x)在R上单调递增,
∴x+3<2,解得x<-1,
故不等式f (2x+3)-f (x)<8的解集为{x|x<-1}.
进阶训练(一) 函数性质的综合应用
1.(2024·西安临潼区二模)下列函数中,既是奇函数又在(-∞,
+∞)上单调递减的是( )
A.y= B.y=x3
C.y=-x|x| D.y=e-x
√
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
C [在A中,y=是奇函数,减区间为(-∞,0),(0,+∞),故A错误;
在B中,y=x3是奇函数,没有减区间,增区间为(-∞,+∞),故B错误;
在C中,y=-x|x|=是奇函数,减区间为(-∞,+∞),故C正确;
在D中,y=e-x是非奇非偶函数,减区间为(-∞,+∞),故D错误.
故选C.]
√
题号
1
3
5
2
4
6
8
7
9
2.(2024·宜宾三模)已知函数f (x)在[2,+∞)上单调递减且对任意x∈R满足f (1+x)=f (3-x),则不等式f (2x-3)>f (5)的解集是( )
A.(-∞,1)∪(4,+∞) B.(-∞,4)
C.(1,+∞) D.(1,4)
题号
1
3
5
2
4
6
8
7
9
D [因为函数f (x)在[2,+∞)上单调递减且对任意x∈R满足f (1+x)=f (3-x),
所以f (x)的图象关于x=2对称,
故f (x)在(-∞,2)上单调递增,
则不等式f (2x-3)>f (5)可转化|2x-3-2|<3,
解得1<x<4.故选D.]
题号
1
3
5
2
4
6
8
7
9
3.(多选)(2025·大理南涧县模拟)函数f (x)在其定义域上的图象是如图所示折线段ABC,其中点A,B,C的坐标分别为(1,2),(-1,0),(-3,2),以下说法中正确的是( )
A.f ( f (-2))=2
B.f (x+1)为偶函数
C.f (x)-1≥0的解集为[-3,-2]∪[0,1]
D.若f (x)在[-3,m]上单调递减,则m的取值范围为(-3,-1]
√
√
√
题号
1
3
5
2
4
6
8
7
9
ACD [由题图可得f (-2)=1,所以f ( f (-2))=f (1)=2,A正确;
由题图可得f (x)的图象关于x=-1对称,所以f (x+1)的图象关于x=-2对称,B错误;
由题图可得f (x)-1≥0,即f (x)≥1的解集为[-3,-2]∪[0,1],C正确;
由题图可得f (x)在[-3,-1]上单调递减,所以m的取值范围为
(-3,-1],D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
4.(多选)(2025·哈尔滨市道里区模拟)已知函数f (x)=-,则函数具有下列性质( )
A.函数f (x)的图象关于点(-1,-1)对称
B.函数f (x)在(-1,+∞)上单调递增
C.函数f (x)的图象过原点
D.函数f (x)的值域为{y|y≠-1}
√
√
√
题号
1
3
5
2
4
6
8
7
9
ACD [函数f (x)=-=-1+,f (-1+x)+f (-1-x)=-1+-1-=-2,
可得f (x)的图象关于点(-1,-1)对称,故A正确;
f (x)=-1+在(-1,+∞)上单调递减,故B错误;
由f (0)=0,可得f (x)的图象经过原点,故C正确;
由f (x)=-1+,可得f (x)的值域为{y|y≠-1},故D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
5.(2025·湖北武汉模拟)已知函数f (x-1)(x∈R)是偶函数,且函数
f (x)的图象关于点(1,0)对称,当x∈[-1,1]时,f (x)=ax-1,则
f (2 024)=( )
A.-1 B.-2 C.0 D.2
√
题号
1
3
5
2
4
6
8
7
9
A [根据题意,函数f (x-1)(x∈R)是偶函数,则函数f (x)图象的对称轴为直线x=-1,则有f (x)=f (-2-x),又由函数f (x)的图象关于点(1,0)成中心对称,则f (x)=-f (2-x),则有f (-2-x)=-f (2-x),则f (x+4)=-f (x),则有f (x+8)=-f (x+4)=f (x),则函数f (x)是周期为8的周期函数,则f (2 024)=f (0+253×8)=f (0)=-1.
故选A.]
题号
1
3
5
2
4
6
8
7
9
6.(2024·江苏苏州期末)已知定义在R上的函数f (x)的图象连续不间断,有下列四个命题:
甲:f (x)是奇函数;
乙:f (x)的图象关于点(2,0)对称;
丙:f (22)=0;
丁:f (x+6)=f (x).
如果有且仅有一个是假命题,则该命题是( )
A.甲 B.乙 C.丙 D.丁
√
题号
1
3
5
2
4
6
8
7
9
D [若甲丁成立,则f (-x)=-f (x),f (x+6)=f (x),
∴f (x+6)=-f (-x),∴f (x)的图象关于点(3,0)对称,
f (22)=f (4)≠0,乙丙不成立,∴甲和丁中有一个为假命题,
若甲乙成立,则f (-x)=-f (x),
f (4-x)=-f (x),∴f (4-x)=f (-x),
函数f (x)的周期为4.
∴f (22)=f (2)=0,∴丙成立,丁不成立,
∵只有一个假命题,即丁为假命题.故选D.]
题号
1
3
5
2
4
6
8
7
9
7.(多选)(2025·山西大同模拟)奇函数f (x)与偶函数g(x)的定义域均为R,且满足f (x)-g(x)=2x,则下列判断正确的是( )
A.f (x)+g(x)≥0
B.f (x)=
C.f (x)在R上单调递增
D.g(x)的值域为(-∞,-1]
√
√
√
题号
1
3
5
2
4
6
8
7
9
BCD [因为f (x)-g(x)=2x,①
所以f (-x)-g(-x)=2-x.
因为f (x)为奇函数,g(x)为偶函数,所以f (-x)=-f (x),g(-x)=g(x),
所以-f (x)-g(x)=2-x,②
由①②得,f (x)=,g(x)=-,则f (x)+g(x)=-2-x<0,故A错误,B,C正确.
因为g(x)=-≤-=-1,所以D正确.故选BCD.]
题号
1
3
5
2
4
6
8
7
9
8.(2025·格尔木市模拟)已知f (x)是定义在R上的奇函数,且满足
f (x+2)=-f (-x),则f (1 000)=________.
0 [因为函数f (x)是定义在R上的奇函数,
由奇函数性质可得,f (0)=0,
又f (x+2)=-f (-x)=f (x),
可得函数f (x)的周期为2,有f (1 000)=f (0)=0.]
0
题号
1
3
5
2
4
6
8
7
9
9.(2024·沧州期末)已知函数f (x)是定义在R上的奇函数,且满足
f (x+1)=f (x-3),当x∈(0,2)时,f (x)=x2-,则f (2 025)=________.
-1 [∵f (x+1)=f (x-3),∴f (x+4)=f (x),
∴4是f (x)的一个周期,
∴f (2 025)=f (4×506+1)=f (1)=1-2=-1.]
-1
谢 谢 !
第二章 函数
思维进阶1 函数性质的综合应用
函数性质的综合应用是历年高考的一个热点内容,经常以客观题出现,通过分析函数的性质特点,结合图象研究函数的性质,往往多种性质结合在一起进行考查.
题型一 函数的奇偶性与单调性
[典例1] (1)设f (x)是R上的偶函数,且在(0,+∞)上单调递减,若x1>0且x1+x2<0,则( )
A.f (x1)>f (x2)
B.f (x1)=f (x2)
C.f (x1)
√
(2)(2024·曲靖麒麟区三模)若定义在R上的函数满足f (x-2)=
-f (2-x),且在(-∞,0)单调递减,f (3)=0,则满足(x-1)f (x)≥0的x的取值范围是( )
A.[-3,0]∪[1,3]
B.(-∞,-3]∪{0}∪[1,3]
C.[-3,0)∪[1,3]
D.[1,+∞)
√
(1)A (2)A [(1)由x1>0,x1+x2<0,得0
∴f (x1)>f (x2).
(2)因为定义在R上的函数满足f (x-2)=-f (2-x),
所以f (x)为奇函数,
因为f (x)在(-∞,0)单调递减,f (3)=0,
所以f (x)在(0,+∞)上单调递减,且f (-3)=-f (3)=0,f (0)=0,
由(x-1)f (x)≥0可得或
即或或x=0,
即1≤x≤3或-3≤x≤0.故选A.]
反思领悟 奇偶性与单调性综合的两种题型及解法
(1)比较大小问题,一般解法是先利用奇偶性,将不在同一单调区间上的两个或多个自变量的函数值,转化为同一单调区间上的自变量的函数值,然后利用单调性比较大小.
(2)抽象不等式问题,解题步骤是:
①将所给的不等式转化为两个函数值的大小关系;
②利用奇偶性得出区间上的单调性,再利用单调性“脱去”函数的符号“f ”,转化为解不等式(组)的问题.
题型二 函数的奇偶性与周期性
[典例2] 已知定义在R上的奇函数f (x)满足f (x+2)=-f (x),当x∈[0,1]时,f (x)单调递增,则( )
A.f (6)
B [∵f (x+2)=-f (x),∴f (x+4)=f ((x+2)+2)=-f (x+2)=
f (x),∴函数f (x)是周期为4的周期函数,
∴f (6)=f (2)=-f (0)=f (0),
f (-7)=f (1),f =f =-f =f ,
又当x∈[0,1]时f (x)单调递增,
∴f (0)
f 中的6,-7,转化到单调区间[0,1]内再比较大小.
题型三 函数性质的综合应用
[典例3] 已知定义在R上的函数f (x)满足f (x+6)=f (x),且y=f (x+3)为偶函数.若f (x)在(0,3)上单调递减,则下列结论正确的是( )
A.f (10)
A [∵f (x+6)=f (x),∴f (x)的周期为6.
又∵y=f (x+3)为偶函数,∴f (x+3)=f (-x+3),∴f (10)=f (4+6)=f (4)=f (1+3)=f (-1+3)=f (2).
∵1<<2,0
反思领悟 对于函数性质结合的题目,函数的周期性有时需要通过函数的奇偶性得到,函数的奇偶性体现的是一种对称关系,而函数的单调性体现的是函数值随自变量变化而变化的规律.因此在解题时,往往需要借助函数的奇偶性和周期性来确定另一区间上的单调性,即实现区间的转换,再利用单调性解决相关问题.
【教用·备选题】
1.(2024·辽宁六校联考)若定义在R上的奇函数f (x)满足f (2-x)=
f (x),在区间(0,1)上,有(x1-x2)[f (x1)-f (x2)]>0,则下列说法正确的是( )
A.函数f (x)的图象关于点(1,0)成中心对称
B.函数f (x)的图象关于直线x=2成轴对称
C.在区间(2,3)上,f (x)单调递减
D.f >f
√
C [f (4-x)=f (2-(x-2))=f (x-2)=-f (2-x)=-f (x),
即f (4-x)+f (x)=0,故f (x)的图象关于点(2,0)成中心对称,B错误;
∵f (2-x)=f (x),则f (x)的图象关于直线x=1成轴对称,A错误;
根据题意可得,f (x)在(0,1)上单调递增,
∵f (x)的图象关于直线x=1成轴对称,关于点(2,0)成中心对称,则f (x)在(2,3)上单调递减,C正确;
又∵f (x)=f (2-x)=-f (x-2),则f (x+2)=-f (x),
∴f (x+4)=-f (x+2)=f (x),可知f (x)的周期为4,
则f =f
2.(2022·全国乙卷)已知函数f (x),g(x)的定义域均为R,且f (x)+g(2-x)=5,g(x)-f (x-4)=7.若y=g(x)的图象关于直线x=2对称,g(2)=4,则=( )
A.-21 B.-22
C.-23 D.-24
√
D [因为y=g(x)的图象关于直线x=2对称,所以g(2-x)=g(x+2),因为g(x)-f (x-4)=7,所以g(x+2)-f (x-2)=7,
即g(x+2)=7+f (x-2),
因为f (x)+g(2-x)=5,所以f (x)+g(x+2)=5,
代入得f (x)+[7+f (x-2)]=5,即f (x)+f (x-2)=-2,
所以f (3)+f (5)+…+f (21)=(-2)×5=-10,
f (4)+f (6)+…+f (22)=(-2)×5=-10.
因为f (x)+g(2-x)=5,所以f (0)+g(2)=5,
即f (0)=1,所以f (2)=-2-f (0)=-3.
因为g(x)-f (x-4)=7,所以g(x+4)-f (x)=7,又因为f (x)+g(2-x)=5,联立得,g(2-x)+g(x+4)=12,
所以y=g(x)的图象关于点(3,6)中心对称,因为函数g(x)的定义域为R,所以g(3)=6,因为f (x)+g(x+2)=5,
所以f (1)=5-g(3)=-1.
所以=f (1)+f (2)+[f (3)+f (5)+…+f (21)]+[f (4)+
f (6)+…+f (22)]=-1-3-10-10=-24.故选D.]
3.(多选)(2024·浙江大学附属中学期中)已知f (x)是定义在R上的奇函数,且y=f (x+1)为偶函数,当x∈(0,1]时,f (x)=-x2,下列结论正确的有( )
A.函数f (x)的周期是4
B.直线x=2 023是函数f (x)图象的一条对称轴
C.f (x)在[2 022,2 023]上单调递减
D.f (2 022)+f (2 023)=1
√
√
√
ABD [对于A,因为函数f (x+1)为偶函数,所以f (x+1)=f (-x+1),即f (x)的图象关于直线x=1对称,因为f (x)为奇函数,所以
f (-x)=-f (x),则f (x+2)=f (-(x+1)+1)=f (-x)=-f (x),
所以f (x+4)=-f (x+2)=f (x),所以f (x)是周期为4的函数,故A正确;
因为f (x)的图象关于直线x=1对称,且为奇函数,所以f (x)的图象关于直线x=-1对称,又f (x)是周期为4的函数,所以f (x)的图象关于直线x=3对称,因为2 023=505×4+3,
所以直线x=2 023是函数f (x)图象的一条对称轴,故B正确;
由f (x)是定义在R上的奇函数,所以f (0)=0,
当x∈(0,1]时,f (x)=-x2,可得当x∈[0,1]时,f (x)=-x2,
令x∈[2,3],则x-2∈[0,1],
所以f (x)=-f (x-2)=(x-2)2,此时f (x)单调递增,
因为2 022=505×4+2,
所以f (x)在[2 022,2 023]上的单调性相当于f (x)在[2,3]上的单调性,故此时单调递增,故C错误;
f (2 022)=f (2)=0,f (2 023)=f (3)=1,
所以f (2 022)+f (2 023)=1,故D正确.故选ABD.]
4.(2024·四川眉山仁寿县期中)定义在R上的函数f (x)满足f (x+y)=f (x)+f (y),f (1)=4.
(1)求f (0)的值;
(2)判断函数f (x)的奇偶性,并证明你的结论;
(3)若函数f (x)在[0,+∞)上单调递增,求不等式f (2x+3)-f (x)<8的解集.
[解] (1)令x=y=0,得f (0)=f (0)+f (0),解得f (0)=0.
(2)因为函数f (x)的定义域为R,令y=-x,
则f (x-x)=f (x)+f (-x),
∴f (x)+f (-x)=0,∴f (-x)=-f (x),
∴函数f (x)为奇函数.
(3)∵f (1)=4,令x=y=1,得f (2)=f (1)+f (1)=8,
∵f (2x+3)-f (x)<8,∴f (2x+3)-f (x)<f (2),
∵f (x+y)=f (x)+f (y),
∴f (2x+3)-f (x)=f (2x+3)+f (-x)=f (x+3),∴f (x+3)<f (2).
∵函数f (x)在[0,+∞)上单调递增,且函数f (x)为奇函数,
∴函数f (x)在R上单调递增,
∴x+3<2,解得x<-1,
故不等式f (2x+3)-f (x)<8的解集为{x|x<-1}.
进阶训练(一) 函数性质的综合应用
1.(2024·西安临潼区二模)下列函数中,既是奇函数又在(-∞,
+∞)上单调递减的是( )
A.y= B.y=x3
C.y=-x|x| D.y=e-x
√
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
C [在A中,y=是奇函数,减区间为(-∞,0),(0,+∞),故A错误;
在B中,y=x3是奇函数,没有减区间,增区间为(-∞,+∞),故B错误;
在C中,y=-x|x|=是奇函数,减区间为(-∞,+∞),故C正确;
在D中,y=e-x是非奇非偶函数,减区间为(-∞,+∞),故D错误.
故选C.]
√
题号
1
3
5
2
4
6
8
7
9
2.(2024·宜宾三模)已知函数f (x)在[2,+∞)上单调递减且对任意x∈R满足f (1+x)=f (3-x),则不等式f (2x-3)>f (5)的解集是( )
A.(-∞,1)∪(4,+∞) B.(-∞,4)
C.(1,+∞) D.(1,4)
题号
1
3
5
2
4
6
8
7
9
D [因为函数f (x)在[2,+∞)上单调递减且对任意x∈R满足f (1+x)=f (3-x),
所以f (x)的图象关于x=2对称,
故f (x)在(-∞,2)上单调递增,
则不等式f (2x-3)>f (5)可转化|2x-3-2|<3,
解得1<x<4.故选D.]
题号
1
3
5
2
4
6
8
7
9
3.(多选)(2025·大理南涧县模拟)函数f (x)在其定义域上的图象是如图所示折线段ABC,其中点A,B,C的坐标分别为(1,2),(-1,0),(-3,2),以下说法中正确的是( )
A.f ( f (-2))=2
B.f (x+1)为偶函数
C.f (x)-1≥0的解集为[-3,-2]∪[0,1]
D.若f (x)在[-3,m]上单调递减,则m的取值范围为(-3,-1]
√
√
√
题号
1
3
5
2
4
6
8
7
9
ACD [由题图可得f (-2)=1,所以f ( f (-2))=f (1)=2,A正确;
由题图可得f (x)的图象关于x=-1对称,所以f (x+1)的图象关于x=-2对称,B错误;
由题图可得f (x)-1≥0,即f (x)≥1的解集为[-3,-2]∪[0,1],C正确;
由题图可得f (x)在[-3,-1]上单调递减,所以m的取值范围为
(-3,-1],D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
4.(多选)(2025·哈尔滨市道里区模拟)已知函数f (x)=-,则函数具有下列性质( )
A.函数f (x)的图象关于点(-1,-1)对称
B.函数f (x)在(-1,+∞)上单调递增
C.函数f (x)的图象过原点
D.函数f (x)的值域为{y|y≠-1}
√
√
√
题号
1
3
5
2
4
6
8
7
9
ACD [函数f (x)=-=-1+,f (-1+x)+f (-1-x)=-1+-1-=-2,
可得f (x)的图象关于点(-1,-1)对称,故A正确;
f (x)=-1+在(-1,+∞)上单调递减,故B错误;
由f (0)=0,可得f (x)的图象经过原点,故C正确;
由f (x)=-1+,可得f (x)的值域为{y|y≠-1},故D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
5.(2025·湖北武汉模拟)已知函数f (x-1)(x∈R)是偶函数,且函数
f (x)的图象关于点(1,0)对称,当x∈[-1,1]时,f (x)=ax-1,则
f (2 024)=( )
A.-1 B.-2 C.0 D.2
√
题号
1
3
5
2
4
6
8
7
9
A [根据题意,函数f (x-1)(x∈R)是偶函数,则函数f (x)图象的对称轴为直线x=-1,则有f (x)=f (-2-x),又由函数f (x)的图象关于点(1,0)成中心对称,则f (x)=-f (2-x),则有f (-2-x)=-f (2-x),则f (x+4)=-f (x),则有f (x+8)=-f (x+4)=f (x),则函数f (x)是周期为8的周期函数,则f (2 024)=f (0+253×8)=f (0)=-1.
故选A.]
题号
1
3
5
2
4
6
8
7
9
6.(2024·江苏苏州期末)已知定义在R上的函数f (x)的图象连续不间断,有下列四个命题:
甲:f (x)是奇函数;
乙:f (x)的图象关于点(2,0)对称;
丙:f (22)=0;
丁:f (x+6)=f (x).
如果有且仅有一个是假命题,则该命题是( )
A.甲 B.乙 C.丙 D.丁
√
题号
1
3
5
2
4
6
8
7
9
D [若甲丁成立,则f (-x)=-f (x),f (x+6)=f (x),
∴f (x+6)=-f (-x),∴f (x)的图象关于点(3,0)对称,
f (22)=f (4)≠0,乙丙不成立,∴甲和丁中有一个为假命题,
若甲乙成立,则f (-x)=-f (x),
f (4-x)=-f (x),∴f (4-x)=f (-x),
函数f (x)的周期为4.
∴f (22)=f (2)=0,∴丙成立,丁不成立,
∵只有一个假命题,即丁为假命题.故选D.]
题号
1
3
5
2
4
6
8
7
9
7.(多选)(2025·山西大同模拟)奇函数f (x)与偶函数g(x)的定义域均为R,且满足f (x)-g(x)=2x,则下列判断正确的是( )
A.f (x)+g(x)≥0
B.f (x)=
C.f (x)在R上单调递增
D.g(x)的值域为(-∞,-1]
√
√
√
题号
1
3
5
2
4
6
8
7
9
BCD [因为f (x)-g(x)=2x,①
所以f (-x)-g(-x)=2-x.
因为f (x)为奇函数,g(x)为偶函数,所以f (-x)=-f (x),g(-x)=g(x),
所以-f (x)-g(x)=2-x,②
由①②得,f (x)=,g(x)=-,则f (x)+g(x)=-2-x<0,故A错误,B,C正确.
因为g(x)=-≤-=-1,所以D正确.故选BCD.]
题号
1
3
5
2
4
6
8
7
9
8.(2025·格尔木市模拟)已知f (x)是定义在R上的奇函数,且满足
f (x+2)=-f (-x),则f (1 000)=________.
0 [因为函数f (x)是定义在R上的奇函数,
由奇函数性质可得,f (0)=0,
又f (x+2)=-f (-x)=f (x),
可得函数f (x)的周期为2,有f (1 000)=f (0)=0.]
0
题号
1
3
5
2
4
6
8
7
9
9.(2024·沧州期末)已知函数f (x)是定义在R上的奇函数,且满足
f (x+1)=f (x-3),当x∈(0,2)时,f (x)=x2-,则f (2 025)=________.
-1 [∵f (x+1)=f (x-3),∴f (x+4)=f (x),
∴4是f (x)的一个周期,
∴f (2 025)=f (4×506+1)=f (1)=1-2=-1.]
-1
谢 谢 !
同课章节目录
