《高考快车道》2026版高三一轮总复习数学(基础版)21 第二章 第10课时 函数的零点与方程的解 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)21 第二章 第10课时 函数的零点与方程的解 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:46 | ||
图片预览










文档简介
(共79张PPT)
第二章 函数
第10课时 函数的零点与方程的解
[考试要求] 1.理解函数的零点与方程的解的联系.
2.理解函数零点存在定理,并能简单应用.
3.了解用二分法求方程的近似解.
考点一 判定函数零点所在区间
1.函数的零点
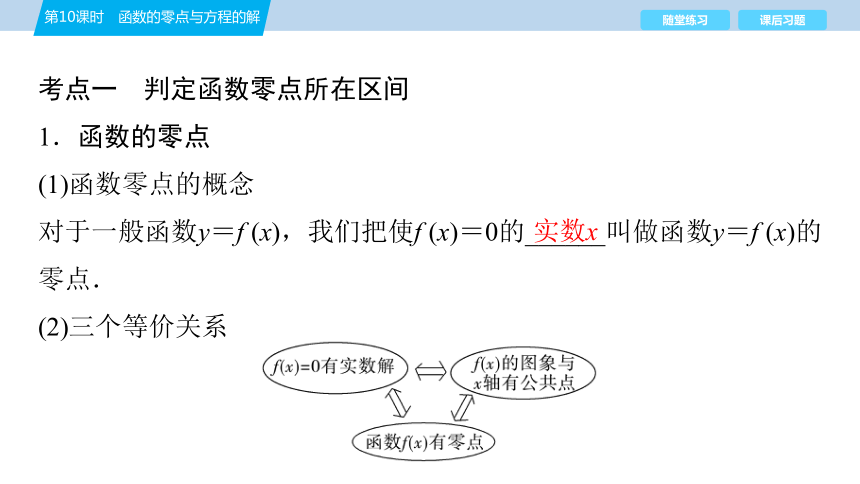
(1)函数零点的概念
对于一般函数y=f (x),我们把使f (x)=0的______叫做函数y=f (x)的零点.
(2)三个等价关系
实数x
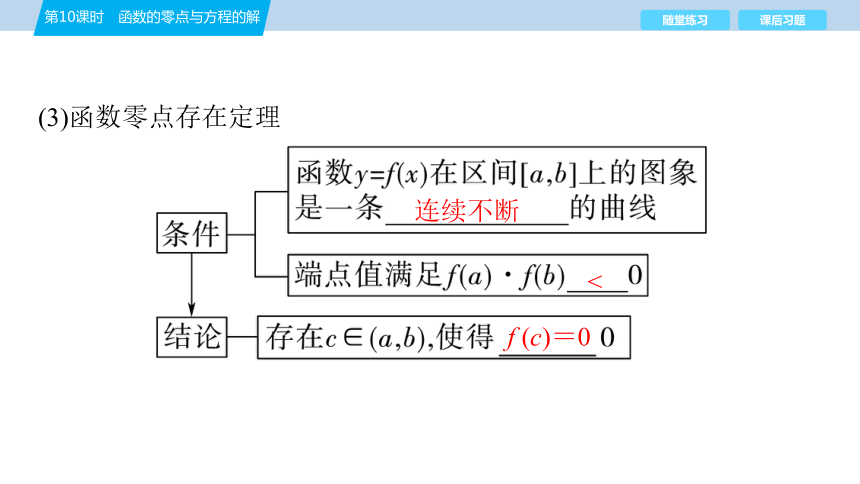
(3)函数零点存在定理
连续不断
<
f (c)=0
2.二分法的定义
对于在区间[a,b]上图象连续不断且f (a)f (b)<0的函数y=f (x),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
提醒:(1)若连续不断的函数f (x)在定义域上是单调函数,则f (x)至多有一个零点.函数的零点不是一个“点”,而是方程f (x)=0的实根.
(2)由函数y=f (x)(图象是连续不断的)在闭区间[a,b]上有零点不一定能推出f (a)·f (b)<0,如图所示,所以“f (a)·f (b)<0”是“y=
f (x)在闭区间[a,b]上有零点”的充分不必要条件.
[典例1] (1)(2025·湖北荆州模拟)若x0是方程的根,则x0属于区间( )
A. B.
C. D.
(2)(人教A版必修第一册P155习题4.5T2改编)已知函数f (x)=e-x-2x-5的零点位于区间(m,m+1)(m∈Z)上,则m=( )
A.-2 B.-1
C.0 D.1
√
√
(1)C (2)A [(1)构造函数f (x)=-,
易知函数f (x)在R上单调递减,且函数f (x)的图象是一条连续不断的曲线,易知f (0)=-0=1>0,f =->0,
f =-<0,结合选项,因为f ·f <0,
故函数f (x)的零点所在的区间为,
即方程的根x0属于区间.
(2)因为函数f (x)=e-x-2x-5是连续的减函数,f (-2)=e2-1>0,
f (-1)=e-3<0,所以f (-2)·f (-1)<0,函数f (x)=e-x-2x-5的零点位于区间(-2,-1),即(m,m+1)上,又m∈Z,所以m=
-2.]
反思领悟 本例(1)解决的关键是将方程根所在的区间转化为函数
f (x)=的零点所在区间,利用零点存在定理对所给选项一一验证即可.本例(2)根据“三个等价关系”解答:①f (x)=e-x-2x-5的零点就是e-x-2x-5=0的根,即y=e-x与y=2x+5图象的交点;②画出函数y=e-x=和y=2x+5的图象,初步判断图象交点所在区间(定性);③利用零点存在定理求m(定量).
巩固迁移1 (1)(2025·湖南长沙模拟)设函数f (x)=x-ln x,则函数y=f (x)( )
A.在区间,(1,e)内均有零点
B.在区间,(1,e)内均无零点
C.在区间内有零点,在区间(1,e)内无零点
D.在区间内无零点,在区间(1,e)内有零点
√
(2)用二分法求函数f (x)=log3(2x+4)-在区间(-1,0)内的零点近似值,至少经过________次二分后精确度达到0.1.( )
A.2 B.3
C.4 D.5
(1)D (2)C [(1)令f (x)=0得x=ln x.
作出函数y=x和y=ln x的图象,如图,
显然y=f (x)在内无零点,在(1,e)内有零点.
√
(2)∵开区间(-1,0)的长度等于1,
每经过一次操作,区间长度变为原来的一半,
经过n次操作后,区间长度变为,
故有<0.1,解得n≥4,
∴至少经过4次二分后精确度达到0.1.]
考点二 确定函数零点个数
函数零点个数的判断方法
(1)直接求零点;
(2)用零点存在定理再结合函数的单调性确定零点个数;
(3)利用函数图象的交点个数判断.
[典例2] (1)函数f (x)=的零点个数为( )
A.3 B.2
C.1 D.0
(2)函数f (x)=ln x+x2-3的零点个数为________.
√
1
(1)B (2)1 [(1)由f (x)=0得,
或
解得x=-2或x=e.
因此函数f (x)共有2个零点.
故选B.
(2)令f (x)=0,可得方程ln x+x2-3=0,即ln x=3-x2,
故原函数的零点个数即为函数y=ln x与y=3-x2图象的交点个数.
在同一平面直角坐标系中作出两个函数的大致图象(如图).
由图可知,函数y=3-x2与y=ln x的图象只有一个交点,
故函数f (x)=ln x+x2-3只有一个零点.]
反思领悟 在本例(1)中,可根据零点的定义直接计算函数零点,进而得出零点个数;本例(2)中,求函数f (x)=ln x+x2-3的零点个数,转化为函数y=3-x2与y=ln x图象的交点个数,作出图象后观察其交点个数即可.
巩固迁移2 已知函数f (x)=则函数g(x)=f (x)-的零点个数为( )
A.0 B.1
C.2 D.3
√
C [当x≤0时,令g(x)=-=0,解得x=1,舍去;当x>0时,令g(x)=|log2x|-=0,解得x=或x=,满足x>0,所以x=或x=.
综上,函数g(x)=f (x)-的零点个数为2.]
考点三 函数零点的应用
考向1 根据函数零点个数求参数
[典例3] (2024·新高考Ⅱ卷)设函数f (x)=a(x+1)2-1,g(x)=cos x+2ax.当x∈(-1,1)时,曲线y=f (x)与y=g(x)恰有一个交点.则
a=( )
A.-1 B.
C.1 D.2
√
D [法一:令f (x)=g(x),
即a(x+1)2-1=cos x+2ax,可得ax2+a-1=cos x,
令F (x)=ax2+a-1,G(x)=cos x,
原题意等价于当x∈(-1,1)时,曲线y=F (x)与y=G(x)恰有一个交点,
注意到F (x),G(x)均为偶函数,可知该交点只能在y轴上,
可得F (0)=G(0),即a-1=1,解得a=2.
若a=2,令F (x)=G(x),可得2x2+1-cos x=0,
因为x∈(-1,1),则2x2≥0,1-cos x≥0,当且仅当x=0时,等号同时成立,
可得2x2+1-cos x≥0,当且仅当x=0时,等号成立,
则方程2x2+1-cos x=0有且仅有一个实根0,即曲线y=F (x)与y=G(x)恰有一个交点,
所以a=2符合题意.
综上所述,a=2.
法二:令h(x)=f (x)-g(x)=ax2+a-1-cos x,x∈(-1,1),
原题意等价于h(x)有且仅有一个零点,
因为h(-x)=a(-x)2+a-1-cos (-x)=ax2+a-1-cos x=h(x),
则h(x)为偶函数,根据偶函数的对称性可知h(x)的零点只能为0,
即h(0)=a-2=0,解得a=2.
若a=2,则h(x)=2x2+1-cos x,x∈(-1,1),又因为2x2≥0,1-cos x≥0,当且仅当x=0时,等号同时成立,可得h(x)≥0,当且仅当x=0时,等号成立,即h(x)有且仅有一个零点0,
所以a=2符合题意.
故选D.]
反思领悟 本例中,解决的关键是根据偶函数图象的特征判定y=
f (x)与y=g(x)何时恰有一个交点.若按原函数的关系来研究曲线的交点,问题会很复杂,可将y=f (x)和y=g(x)合并后再重新组合,借助偶函数来求解.
巩固迁移3 (2025·济南模拟)已知函数f (x)=若函数g(x)=f (x)-m有三个零点,则实数m的取值范围是( )
A.(1,2] B.(1,2)
C.(0,1) D.[1,+∞)
√
A [因为函数g(x)=f (x)-m有三个零点,所以函数y=f (x)的图象与直线y=m有三个不同的交点,作出函数f (x)的图象如图所示.由图可知,1考向2 根据函数零点的范围求参数
[典例4] 函数f (x)=2x--a的零点在区间(1,2)内,则实数a的取值范围是( )
A.0C.1√
A [因为函数y=2x,y=-在(0,+∞)上均单调递增,所以函数
f (x)=2x--a在(0,+∞)上单调递增,由函数f (x)=2x--a的零点在区间(1,2)内,得解得0反思领悟 本例解题的关键是先判断函数的单调性,再结合零点存在定理,解即得a的取值范围.
巩固迁移4 函数f (x)=2alog2x+a·4x+3在区间上有零点,则实数a的取值范围是( )
A.a<- B.a<-
C.-√
D [当a=0时,f (x)=3,不符合题意;
当a>0时,由于函数y=2alog2x,y=a·4x+3在上均单调递增,此时函数f (x)在上单调递增;
当a<0时,由于函数y=2alog2x,y=a·4x+3在上均单调递减,此时函数f (x)在上单调递减.
因为函数f (x)在区间上有零点,所以f f (1)<0,
即3(4a+3)<0,解得a<-.]
形如y=f (g(x))的复合函数(称此函数为嵌套函数)零点相关问题综合性较强,难度稍大,主要涉及判断函数零点的个数或范围.对于嵌套函数的零点,通常先“换元解套”,将复合函数拆解为两个相对简单的函数,借助函数的图象、性质求解.
[典例] 函数f (x)=若函数g(x)=f ( f (x))-a有三个不同的零点,则实数a的取值范围是___________.
[-1,+∞) [设t=f (x),令f ( f (x))-a=0,则a=f (t).
在同一坐标系内作y=a,y=f (t)的图象(如图).
[-1,+∞)
当a<-1时,y=a与y=f (t)的图象有一个交点,不符合题意;
当a≥-1时,y=a与y=f (t)的图象有两个交点.
设交点的横坐标为t1,t2(不妨设t2>t1),则t1<-1,t2≥-1.
当t1<-1时,t1=f (x)有一解;
当t2≥-1时,t2=f (x)有两解.
综上,当a≥-1时,函数g(x)=f ( f (x))-a有三个不同的零点.]
反思领悟 该类问题考查复合函数的零点的判断,利用换元法和数形结合思想是解决本类问题的关键.含参数的嵌套函数方程,应注意让参数的取值“动起来”,抓临界位置,动静结合,如本例由y=a与y=f (t)的图象,确定t1,t2的取值范围,进而由y=f (x)与y=t的图象确定零点的个数.
应用体验 (1)已知函数f (x)=则方程f ( f (x))=1的
实数根的个数为( )
A.7 B.5
C.3 D.2
(2)已知f (x)=|3x-1|+2,若关于x的方程-(2+a)f (x)+2a=0有三个实根,则实数a的取值范围是( )
A.12
C.23
√
√
(1)B (2)C [(1)令f (x)=t,则f (t)=1.
①当t≤2时,2|t|-1=1,∴2|t|=2,∴|t|=1,即t=±1.
②当t>2时,=1,∴t=3.
画出函数f (x)的图象,如图所示,若t=-1,即f (x)=-1,无解;
若t=1,直线y=t=1与y=f (x)的图象有3个交点,
即f ( f (x))=1有3个不同实根;
若t=3,直线y=t=3与y=f (x)的图象有2个交点,
即f ( f (x))=1有2个不同实根.
综上所述,方程f ( f (x))=1的实数根的个数为5.故选B.
(2)因为[f (x)]2-(2+a)f (x)+2a=0,所以f (x)=2或f (x)=a,作出函数f (x)的图象如图所示,由图可得f (x)=2有一个实根0,所以要使
f (x)=a有两个不同非零实根,只需2随堂练习
√
1.(人教A版必修第一册P155习题4.5T4改编)函数y=-ln x的零点所在区间是( )
A.(3,4) B.(2,3)
C.(1,2) D.(0,1)
B [因为函数的定义域为(0,+∞),且函数y=在(0,+∞)上单调递减,y=-ln x在(0,+∞)上单调递减,所以函数y=-ln x在(0,+∞)上是减函数.又当x=2时,y=-ln 2>0;当x=3时,y=1-
ln 3<0,两函数值异号,所以函数y=-ln x的零点所在区间是(2,3).]
2.(2025·重庆模拟)函数f (x)=ex+x-3在区间(0,1)上的零点个数是( )
A.0 B.1
C.2 D.3
√
B [由题知函数f (x)是增函数.根据函数零点存在定理及f (0)=
-2<0,f (1)=e-2>0,f (0)·f (1)<0,可知函数f (x)在区间(0,1)上有且只有一个零点.故选B.]
3.已知函数f (x)=若函数g(x)=f (x)-m有3个零点,则实数m的取值范围是( )
A.(-∞,0) B.
C.(1,+∞) D.(0,1)
√
D [令g(x)=f (x)-m=0,得f (x)=m,根据分段函数f (x)的解析式,作出函数f (x)的图象,如图所示.由题可知函数y=f (x)的图象和直线y=m有3个交点,根据图象可得实数m的取值范围是(0,1).]
4.已知函数f (x)=g(x)=f (x)-x+a,若g(x)存在3个零点,则实数a的取值范围为________.
[函数g(x)=f (x)-x+a存在3个零点,等价于函数f (x)的图象与y=x-a的图象有3个交点.画出函数f (x)和y=x-a的图象如图所示.根据图象易知,要使函数f (x)和y=x-a的图象有3个交点,则-<-a≤0,即0≤a<.]
【教用·备选题】
1.(2025·毕节市模拟)已知x1是函数f (x)=ex+x-2的零点,x2是函数g(x)=e4-x-x+2的零点,则x1+x2的值为( )
A.3 B.4
C.5 D.6
√
B [因为x1是函数f (x)=ex+x-2的零点,
所以+x1-2=0,即=2-x1.
因为x2是函数g(x)=e4-x-x+2的零点,
所以-x2+2=0,即=x2-2.令t=4-x2,
则x2=4-t,所以et=4-t-2=2-t,所以=et,
即x1=t=4-x2,所以x1+x2=4.
故选B.]
2.(2024·六安市金安区期末)若函数f (x)=若关
于x的方程f 2(x)+(1-a)f (x)-a=0恰有两个不同实数根,则实数a的取值范围为( )
A.(0,3) B.[1,3)
C.(1,3) D.[1,3]
√
B [由题意可得,[f (x)-a][f (x)+1]=0,
∴f (x)=a 或f (x)=-1,
画出函数f (x)的图象如图所示,
观察可得,f (x)=-1没有实数根,
则原问题转化为方程f (x)=a有两个不同的实数根,
注意到函数的最大值为f (2)=3,
故1≤a<3,即实数a的取值范围是[1,3).故选B.]
3.(多选)(2025·福建三明模拟)已知a是方程ex+x-4=0的实根,则下列各数为正数的是( )
A.a2-2a B.ea-2
C.ln a D.a2-a3
√
√
BC [令f (x)=ex+x-4,x∈R,因为y=ex与y=x-4在R上均单调递增,
所以f (x)在R上单调递增,又因为f (1)=e-3<0,f (2)=e2-2>0,
所以函数y=f (x)只有一个零点,且位于区间(1,2),所以a∈(1,2).
对于A,由二次函数的性质可知当a∈(1,2)时,a2-2a<0,不符合题意;
对于B,当a∈(1,2)时,ea∈(e,e2),
所以ea-2>e-2>0,符合题意;
对于C,当a∈(1,2)时,由对数函数的性质可知ln a>0,满足题意;
对于D,当a∈(1,2)时,a2-a3=a2(1-a)<0,不符题意.
故选BC.]
4.(多选)(2025·青海模拟)设函数f (x)=若函
数g(x)=f (x)-a恰有2个零点,则实数a的值可能为( )
A. B.
C. D.3
√
√
AC [令g(x)=f (x)-a=0,得f (x)=a,
即直线y=a与y=f (x)的图象有两个交点,
由题意可知,当x<1时,f (x)=2x+1单调递增,且2x+1>1.
当x≥1时,f (x)=单调递减,
作出f (x)的大致图象,如图所示.
由图可知,当a∈(1,3)时,
g(x)=f (x)-a恰有2个零点.
故选AC.]
课后习题(十五) 函数的零点与方程的解
1.(人教A版必修第一册P144练习T1改编)已知函数f (x)在区间[a,b]上单调,且图象是连续不断的,若f (a)f (b)<0,则方程f (x)=0在区间[a,b]上( )
A.至少有一实数解 B.至多有一实数解
C.没有实数解 D.必有唯一的实数解
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [∵f (x)为连续函数,且f (a)f (b)<0,
∴函数f (x)在区间[a,b]上至少有一个零点,
∵函数f (x)在区间[a,b]上单调,∴函数f (x)在区间[a,b]上至多有一个零点,
故函数f (x)在区间[a,b]上有且只有一个零点,即方程f (x)=0在区间[a,b]内必有唯一的实数解.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(北师大版必修第一册P131例1改编)函数f (x)=x+log2x的零点所在的区间为( )
A. B.
C. D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [f (x)=x+log2x在(0,+∞)上单调递增,
f =+log2=-log23<-log22
=-<0,f =+log2=-<0,
f =+log2=-log23==(log232-log227)>0,则函数f (x)=x+log2x的零点所在的区间为.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教A版必修第一册P143例1改编)函数f (x)=2x|log2x|-1的零点个数为( )
A.0 B.1
C.2 D.4
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [令f (x)=0,得|log2x|=,在同一平面直角坐标系中分别作出函数y=|log2x|与y=的图象如图所示,由图可知,函数y=|log2x|与y=的图象有2个交点,即函数f (x)有2个零点.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(多选)(人教A版必修第一册P160复习参考题4T4改编)已知函数f (x)=对于方程f (x)=k(k<0),下列说法正确的是
( )
A.当k<-4时,f (x)=k有1个解
B.若f (x)=k有2个解,则k>-3
C.当-4D.f (x)=k可能有4个解
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AC [作出f (x)的图象与直线y=k,如图.
由图象可知,
当k<-4时,f (x)=k有1个解,A正确;
当k=-4或k>-3时,f (x)=k有2个解,B错误;
当-4f (x)=k不可能有4个解,D错误.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·北京学业考试)函数f (x)=x(x2+1)的零点为( )
A.-1 B.0
C.1 D.2
√
B [令f (x)=x(x2+1)=0,则x=0,
即函数f (x)=x(x2+1)的零点为0.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·广州越秀区期末)函数f (x)=x+ln x-5的零点所在的一个区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由题意,x>0,函数f (x)=x+ln x-5在定义域上单调递增,
f (1)=1+ln 1-5=-4<0,f (2)=2+ln 2-5<2+ln e-5=-2<0,
f (3)=3+ln 3-5<3+ln e2-5=0,f (4)=4+ln 4-5>4+ln e-5=0,
∴零点所在的一个区间是(3,4).故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2025·漯河模拟)函数f (x)=ln x+x2+a,则“a<-1”是“函数f (x)在(1,e)上存在零点”的( )
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为f (x)=ln x+x2+a,x>0,y=ln x和y=x2在(0,+∞)上单调递增,所以f (x)=ln x+x2+a在(0,+∞)上单调递增,
当函数在(1,e)上存在零点时,则有
解得-1-e2<a<-1,又因为(-1-e2,-1) (-∞,-1),
所以“a<-1”是“函数f (x)在(1,e)上存在零点”的必要不充分条件.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2025·渭南模拟)函数f (x)=3x|log2x|-1的零点个数为( )
A.0 B.1
C.2 D.3
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [函数f (x)=3x|log2x|-1的零点,
即3x|log2x|-1=0的解,
即|log2x|=的解,
即y=|log2x|与y=图象的交点,如图所示,
从函数图象可知,y=|log2x|与y=的图象有2个交点,即函数f (x)的零点个数为2.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·北京通州区期末)已知函数f (x)=若g(x)
=f (x)-a有3个零点,则a的取值范围为( )
A.(-1,0) B.
C. D.∪{-1}
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [设h(x)=(x>0),则h′(x)=,
令h′(x)>0,解得0<x<e,令h′(x)<0,解得x>e,
所以函数h(x)在(0,e)单调递增,在(e,+∞)单调递减.
所以h(x)max=.因为g(x)=f (x)-a=0,
所以f (x)=a有三个根.
作出函数y=f (x)和y=a的图象如图所示,
所以a的取值范围为.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·广东模拟)若函数f (x)=|2x-3|-1-m只有1个零点,则m的取值范围是_________________.
[2,+∞)∪{-1}
题号
1
3
5
2
4
6
8
7
9
10
11
12
[2,+∞)∪{-1} [由f (x)=|2x-3|-1-m=0,得|2x-3|-1=m.
设函数g(x)=|2x-3|-1=
作出g(x)的大致图象,如图所示.
由图可知,m的取值范围是[2,+∞)∪{-1}.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2025·天津红桥区模拟)对实数a和b,定义运算“ ”:a b=设函数f (x)=(x2-2) (x-x2),x∈R,若函数y=f (x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是_________
____________.
∪
[2,+∞)
题号
1
3
5
2
4
6
8
7
9
10
11
12
∪[2,+∞) [∵a b=
∴函数f (x)=(x2-2) (x-x2)=
由图可知,当-c∈(-∞,-2],
即c∈∪[2,+∞)时,
函数f (x) 与y=-c的图象有两个公共点,
∴实数c的取值范围是∪[2,+∞).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2025·海南模拟)已知函数f (x)是定义域为R的奇函数,当x>0时,f (x)=x2-2x.
(1)求出函数f (x)在R上的解析式;
(2)画出函数f (x)的图象,并写出单调区间;
(3)若y=f (x)的图象与y=m有3个交点,求实数m的取值范围.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)①由于函数f (x)是定义域为R的奇函数,f (0)=0;
②当x<0时,-x>0,因为f (x)是奇函数,
所以f (-x)=-f (x).
所以f (x)=-f (-x)=-[(-x)2+2x]=-x2-2x,
综上,函数f (x)在R上的解析式为
f (x)=
(2)图象如图所示,
单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
(3)因为方程f (x)=m有三个不同的解,由图象可知,满足题意的m的取值范围为(-1,1).
谢 谢 !
第二章 函数
第10课时 函数的零点与方程的解
[考试要求] 1.理解函数的零点与方程的解的联系.
2.理解函数零点存在定理,并能简单应用.
3.了解用二分法求方程的近似解.
考点一 判定函数零点所在区间
1.函数的零点
(1)函数零点的概念
对于一般函数y=f (x),我们把使f (x)=0的______叫做函数y=f (x)的零点.
(2)三个等价关系
实数x
(3)函数零点存在定理
连续不断
<
f (c)=0
2.二分法的定义
对于在区间[a,b]上图象连续不断且f (a)f (b)<0的函数y=f (x),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
提醒:(1)若连续不断的函数f (x)在定义域上是单调函数,则f (x)至多有一个零点.函数的零点不是一个“点”,而是方程f (x)=0的实根.
(2)由函数y=f (x)(图象是连续不断的)在闭区间[a,b]上有零点不一定能推出f (a)·f (b)<0,如图所示,所以“f (a)·f (b)<0”是“y=
f (x)在闭区间[a,b]上有零点”的充分不必要条件.
[典例1] (1)(2025·湖北荆州模拟)若x0是方程的根,则x0属于区间( )
A. B.
C. D.
(2)(人教A版必修第一册P155习题4.5T2改编)已知函数f (x)=e-x-2x-5的零点位于区间(m,m+1)(m∈Z)上,则m=( )
A.-2 B.-1
C.0 D.1
√
√
(1)C (2)A [(1)构造函数f (x)=-,
易知函数f (x)在R上单调递减,且函数f (x)的图象是一条连续不断的曲线,易知f (0)=-0=1>0,f =->0,
f =-<0,结合选项,因为f ·f <0,
故函数f (x)的零点所在的区间为,
即方程的根x0属于区间.
(2)因为函数f (x)=e-x-2x-5是连续的减函数,f (-2)=e2-1>0,
f (-1)=e-3<0,所以f (-2)·f (-1)<0,函数f (x)=e-x-2x-5的零点位于区间(-2,-1),即(m,m+1)上,又m∈Z,所以m=
-2.]
反思领悟 本例(1)解决的关键是将方程根所在的区间转化为函数
f (x)=的零点所在区间,利用零点存在定理对所给选项一一验证即可.本例(2)根据“三个等价关系”解答:①f (x)=e-x-2x-5的零点就是e-x-2x-5=0的根,即y=e-x与y=2x+5图象的交点;②画出函数y=e-x=和y=2x+5的图象,初步判断图象交点所在区间(定性);③利用零点存在定理求m(定量).
巩固迁移1 (1)(2025·湖南长沙模拟)设函数f (x)=x-ln x,则函数y=f (x)( )
A.在区间,(1,e)内均有零点
B.在区间,(1,e)内均无零点
C.在区间内有零点,在区间(1,e)内无零点
D.在区间内无零点,在区间(1,e)内有零点
√
(2)用二分法求函数f (x)=log3(2x+4)-在区间(-1,0)内的零点近似值,至少经过________次二分后精确度达到0.1.( )
A.2 B.3
C.4 D.5
(1)D (2)C [(1)令f (x)=0得x=ln x.
作出函数y=x和y=ln x的图象,如图,
显然y=f (x)在内无零点,在(1,e)内有零点.
√
(2)∵开区间(-1,0)的长度等于1,
每经过一次操作,区间长度变为原来的一半,
经过n次操作后,区间长度变为,
故有<0.1,解得n≥4,
∴至少经过4次二分后精确度达到0.1.]
考点二 确定函数零点个数
函数零点个数的判断方法
(1)直接求零点;
(2)用零点存在定理再结合函数的单调性确定零点个数;
(3)利用函数图象的交点个数判断.
[典例2] (1)函数f (x)=的零点个数为( )
A.3 B.2
C.1 D.0
(2)函数f (x)=ln x+x2-3的零点个数为________.
√
1
(1)B (2)1 [(1)由f (x)=0得,
或
解得x=-2或x=e.
因此函数f (x)共有2个零点.
故选B.
(2)令f (x)=0,可得方程ln x+x2-3=0,即ln x=3-x2,
故原函数的零点个数即为函数y=ln x与y=3-x2图象的交点个数.
在同一平面直角坐标系中作出两个函数的大致图象(如图).
由图可知,函数y=3-x2与y=ln x的图象只有一个交点,
故函数f (x)=ln x+x2-3只有一个零点.]
反思领悟 在本例(1)中,可根据零点的定义直接计算函数零点,进而得出零点个数;本例(2)中,求函数f (x)=ln x+x2-3的零点个数,转化为函数y=3-x2与y=ln x图象的交点个数,作出图象后观察其交点个数即可.
巩固迁移2 已知函数f (x)=则函数g(x)=f (x)-的零点个数为( )
A.0 B.1
C.2 D.3
√
C [当x≤0时,令g(x)=-=0,解得x=1,舍去;当x>0时,令g(x)=|log2x|-=0,解得x=或x=,满足x>0,所以x=或x=.
综上,函数g(x)=f (x)-的零点个数为2.]
考点三 函数零点的应用
考向1 根据函数零点个数求参数
[典例3] (2024·新高考Ⅱ卷)设函数f (x)=a(x+1)2-1,g(x)=cos x+2ax.当x∈(-1,1)时,曲线y=f (x)与y=g(x)恰有一个交点.则
a=( )
A.-1 B.
C.1 D.2
√
D [法一:令f (x)=g(x),
即a(x+1)2-1=cos x+2ax,可得ax2+a-1=cos x,
令F (x)=ax2+a-1,G(x)=cos x,
原题意等价于当x∈(-1,1)时,曲线y=F (x)与y=G(x)恰有一个交点,
注意到F (x),G(x)均为偶函数,可知该交点只能在y轴上,
可得F (0)=G(0),即a-1=1,解得a=2.
若a=2,令F (x)=G(x),可得2x2+1-cos x=0,
因为x∈(-1,1),则2x2≥0,1-cos x≥0,当且仅当x=0时,等号同时成立,
可得2x2+1-cos x≥0,当且仅当x=0时,等号成立,
则方程2x2+1-cos x=0有且仅有一个实根0,即曲线y=F (x)与y=G(x)恰有一个交点,
所以a=2符合题意.
综上所述,a=2.
法二:令h(x)=f (x)-g(x)=ax2+a-1-cos x,x∈(-1,1),
原题意等价于h(x)有且仅有一个零点,
因为h(-x)=a(-x)2+a-1-cos (-x)=ax2+a-1-cos x=h(x),
则h(x)为偶函数,根据偶函数的对称性可知h(x)的零点只能为0,
即h(0)=a-2=0,解得a=2.
若a=2,则h(x)=2x2+1-cos x,x∈(-1,1),又因为2x2≥0,1-cos x≥0,当且仅当x=0时,等号同时成立,可得h(x)≥0,当且仅当x=0时,等号成立,即h(x)有且仅有一个零点0,
所以a=2符合题意.
故选D.]
反思领悟 本例中,解决的关键是根据偶函数图象的特征判定y=
f (x)与y=g(x)何时恰有一个交点.若按原函数的关系来研究曲线的交点,问题会很复杂,可将y=f (x)和y=g(x)合并后再重新组合,借助偶函数来求解.
巩固迁移3 (2025·济南模拟)已知函数f (x)=若函数g(x)=f (x)-m有三个零点,则实数m的取值范围是( )
A.(1,2] B.(1,2)
C.(0,1) D.[1,+∞)
√
A [因为函数g(x)=f (x)-m有三个零点,所以函数y=f (x)的图象与直线y=m有三个不同的交点,作出函数f (x)的图象如图所示.由图可知,1
[典例4] 函数f (x)=2x--a的零点在区间(1,2)内,则实数a的取值范围是( )
A.0
A [因为函数y=2x,y=-在(0,+∞)上均单调递增,所以函数
f (x)=2x--a在(0,+∞)上单调递增,由函数f (x)=2x--a的零点在区间(1,2)内,得解得0
巩固迁移4 函数f (x)=2alog2x+a·4x+3在区间上有零点,则实数a的取值范围是( )
A.a<- B.a<-
C.-
D [当a=0时,f (x)=3,不符合题意;
当a>0时,由于函数y=2alog2x,y=a·4x+3在上均单调递增,此时函数f (x)在上单调递增;
当a<0时,由于函数y=2alog2x,y=a·4x+3在上均单调递减,此时函数f (x)在上单调递减.
因为函数f (x)在区间上有零点,所以f f (1)<0,
即3(4a+3)<0,解得a<-.]
形如y=f (g(x))的复合函数(称此函数为嵌套函数)零点相关问题综合性较强,难度稍大,主要涉及判断函数零点的个数或范围.对于嵌套函数的零点,通常先“换元解套”,将复合函数拆解为两个相对简单的函数,借助函数的图象、性质求解.
[典例] 函数f (x)=若函数g(x)=f ( f (x))-a有三个不同的零点,则实数a的取值范围是___________.
[-1,+∞) [设t=f (x),令f ( f (x))-a=0,则a=f (t).
在同一坐标系内作y=a,y=f (t)的图象(如图).
[-1,+∞)
当a<-1时,y=a与y=f (t)的图象有一个交点,不符合题意;
当a≥-1时,y=a与y=f (t)的图象有两个交点.
设交点的横坐标为t1,t2(不妨设t2>t1),则t1<-1,t2≥-1.
当t1<-1时,t1=f (x)有一解;
当t2≥-1时,t2=f (x)有两解.
综上,当a≥-1时,函数g(x)=f ( f (x))-a有三个不同的零点.]
反思领悟 该类问题考查复合函数的零点的判断,利用换元法和数形结合思想是解决本类问题的关键.含参数的嵌套函数方程,应注意让参数的取值“动起来”,抓临界位置,动静结合,如本例由y=a与y=f (t)的图象,确定t1,t2的取值范围,进而由y=f (x)与y=t的图象确定零点的个数.
应用体验 (1)已知函数f (x)=则方程f ( f (x))=1的
实数根的个数为( )
A.7 B.5
C.3 D.2
(2)已知f (x)=|3x-1|+2,若关于x的方程-(2+a)f (x)+2a=0有三个实根,则实数a的取值范围是( )
A.1
C.2
√
√
(1)B (2)C [(1)令f (x)=t,则f (t)=1.
①当t≤2时,2|t|-1=1,∴2|t|=2,∴|t|=1,即t=±1.
②当t>2时,=1,∴t=3.
画出函数f (x)的图象,如图所示,若t=-1,即f (x)=-1,无解;
若t=1,直线y=t=1与y=f (x)的图象有3个交点,
即f ( f (x))=1有3个不同实根;
若t=3,直线y=t=3与y=f (x)的图象有2个交点,
即f ( f (x))=1有2个不同实根.
综上所述,方程f ( f (x))=1的实数根的个数为5.故选B.
(2)因为[f (x)]2-(2+a)f (x)+2a=0,所以f (x)=2或f (x)=a,作出函数f (x)的图象如图所示,由图可得f (x)=2有一个实根0,所以要使
f (x)=a有两个不同非零实根,只需2
√
1.(人教A版必修第一册P155习题4.5T4改编)函数y=-ln x的零点所在区间是( )
A.(3,4) B.(2,3)
C.(1,2) D.(0,1)
B [因为函数的定义域为(0,+∞),且函数y=在(0,+∞)上单调递减,y=-ln x在(0,+∞)上单调递减,所以函数y=-ln x在(0,+∞)上是减函数.又当x=2时,y=-ln 2>0;当x=3时,y=1-
ln 3<0,两函数值异号,所以函数y=-ln x的零点所在区间是(2,3).]
2.(2025·重庆模拟)函数f (x)=ex+x-3在区间(0,1)上的零点个数是( )
A.0 B.1
C.2 D.3
√
B [由题知函数f (x)是增函数.根据函数零点存在定理及f (0)=
-2<0,f (1)=e-2>0,f (0)·f (1)<0,可知函数f (x)在区间(0,1)上有且只有一个零点.故选B.]
3.已知函数f (x)=若函数g(x)=f (x)-m有3个零点,则实数m的取值范围是( )
A.(-∞,0) B.
C.(1,+∞) D.(0,1)
√
D [令g(x)=f (x)-m=0,得f (x)=m,根据分段函数f (x)的解析式,作出函数f (x)的图象,如图所示.由题可知函数y=f (x)的图象和直线y=m有3个交点,根据图象可得实数m的取值范围是(0,1).]
4.已知函数f (x)=g(x)=f (x)-x+a,若g(x)存在3个零点,则实数a的取值范围为________.
[函数g(x)=f (x)-x+a存在3个零点,等价于函数f (x)的图象与y=x-a的图象有3个交点.画出函数f (x)和y=x-a的图象如图所示.根据图象易知,要使函数f (x)和y=x-a的图象有3个交点,则-<-a≤0,即0≤a<.]
【教用·备选题】
1.(2025·毕节市模拟)已知x1是函数f (x)=ex+x-2的零点,x2是函数g(x)=e4-x-x+2的零点,则x1+x2的值为( )
A.3 B.4
C.5 D.6
√
B [因为x1是函数f (x)=ex+x-2的零点,
所以+x1-2=0,即=2-x1.
因为x2是函数g(x)=e4-x-x+2的零点,
所以-x2+2=0,即=x2-2.令t=4-x2,
则x2=4-t,所以et=4-t-2=2-t,所以=et,
即x1=t=4-x2,所以x1+x2=4.
故选B.]
2.(2024·六安市金安区期末)若函数f (x)=若关
于x的方程f 2(x)+(1-a)f (x)-a=0恰有两个不同实数根,则实数a的取值范围为( )
A.(0,3) B.[1,3)
C.(1,3) D.[1,3]
√
B [由题意可得,[f (x)-a][f (x)+1]=0,
∴f (x)=a 或f (x)=-1,
画出函数f (x)的图象如图所示,
观察可得,f (x)=-1没有实数根,
则原问题转化为方程f (x)=a有两个不同的实数根,
注意到函数的最大值为f (2)=3,
故1≤a<3,即实数a的取值范围是[1,3).故选B.]
3.(多选)(2025·福建三明模拟)已知a是方程ex+x-4=0的实根,则下列各数为正数的是( )
A.a2-2a B.ea-2
C.ln a D.a2-a3
√
√
BC [令f (x)=ex+x-4,x∈R,因为y=ex与y=x-4在R上均单调递增,
所以f (x)在R上单调递增,又因为f (1)=e-3<0,f (2)=e2-2>0,
所以函数y=f (x)只有一个零点,且位于区间(1,2),所以a∈(1,2).
对于A,由二次函数的性质可知当a∈(1,2)时,a2-2a<0,不符合题意;
对于B,当a∈(1,2)时,ea∈(e,e2),
所以ea-2>e-2>0,符合题意;
对于C,当a∈(1,2)时,由对数函数的性质可知ln a>0,满足题意;
对于D,当a∈(1,2)时,a2-a3=a2(1-a)<0,不符题意.
故选BC.]
4.(多选)(2025·青海模拟)设函数f (x)=若函
数g(x)=f (x)-a恰有2个零点,则实数a的值可能为( )
A. B.
C. D.3
√
√
AC [令g(x)=f (x)-a=0,得f (x)=a,
即直线y=a与y=f (x)的图象有两个交点,
由题意可知,当x<1时,f (x)=2x+1单调递增,且2x+1>1.
当x≥1时,f (x)=单调递减,
作出f (x)的大致图象,如图所示.
由图可知,当a∈(1,3)时,
g(x)=f (x)-a恰有2个零点.
故选AC.]
课后习题(十五) 函数的零点与方程的解
1.(人教A版必修第一册P144练习T1改编)已知函数f (x)在区间[a,b]上单调,且图象是连续不断的,若f (a)f (b)<0,则方程f (x)=0在区间[a,b]上( )
A.至少有一实数解 B.至多有一实数解
C.没有实数解 D.必有唯一的实数解
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [∵f (x)为连续函数,且f (a)f (b)<0,
∴函数f (x)在区间[a,b]上至少有一个零点,
∵函数f (x)在区间[a,b]上单调,∴函数f (x)在区间[a,b]上至多有一个零点,
故函数f (x)在区间[a,b]上有且只有一个零点,即方程f (x)=0在区间[a,b]内必有唯一的实数解.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(北师大版必修第一册P131例1改编)函数f (x)=x+log2x的零点所在的区间为( )
A. B.
C. D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [f (x)=x+log2x在(0,+∞)上单调递增,
f =+log2=-log23<-log22
=-<0,f =+log2=-<0,
f =+log2=-log23==(log232-log227)>0,则函数f (x)=x+log2x的零点所在的区间为.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教A版必修第一册P143例1改编)函数f (x)=2x|log2x|-1的零点个数为( )
A.0 B.1
C.2 D.4
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [令f (x)=0,得|log2x|=,在同一平面直角坐标系中分别作出函数y=|log2x|与y=的图象如图所示,由图可知,函数y=|log2x|与y=的图象有2个交点,即函数f (x)有2个零点.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(多选)(人教A版必修第一册P160复习参考题4T4改编)已知函数f (x)=对于方程f (x)=k(k<0),下列说法正确的是
( )
A.当k<-4时,f (x)=k有1个解
B.若f (x)=k有2个解,则k>-3
C.当-4
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AC [作出f (x)的图象与直线y=k,如图.
由图象可知,
当k<-4时,f (x)=k有1个解,A正确;
当k=-4或k>-3时,f (x)=k有2个解,B错误;
当-4
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·北京学业考试)函数f (x)=x(x2+1)的零点为( )
A.-1 B.0
C.1 D.2
√
B [令f (x)=x(x2+1)=0,则x=0,
即函数f (x)=x(x2+1)的零点为0.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·广州越秀区期末)函数f (x)=x+ln x-5的零点所在的一个区间是( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由题意,x>0,函数f (x)=x+ln x-5在定义域上单调递增,
f (1)=1+ln 1-5=-4<0,f (2)=2+ln 2-5<2+ln e-5=-2<0,
f (3)=3+ln 3-5<3+ln e2-5=0,f (4)=4+ln 4-5>4+ln e-5=0,
∴零点所在的一个区间是(3,4).故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2025·漯河模拟)函数f (x)=ln x+x2+a,则“a<-1”是“函数f (x)在(1,e)上存在零点”的( )
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为f (x)=ln x+x2+a,x>0,y=ln x和y=x2在(0,+∞)上单调递增,所以f (x)=ln x+x2+a在(0,+∞)上单调递增,
当函数在(1,e)上存在零点时,则有
解得-1-e2<a<-1,又因为(-1-e2,-1) (-∞,-1),
所以“a<-1”是“函数f (x)在(1,e)上存在零点”的必要不充分条件.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2025·渭南模拟)函数f (x)=3x|log2x|-1的零点个数为( )
A.0 B.1
C.2 D.3
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [函数f (x)=3x|log2x|-1的零点,
即3x|log2x|-1=0的解,
即|log2x|=的解,
即y=|log2x|与y=图象的交点,如图所示,
从函数图象可知,y=|log2x|与y=的图象有2个交点,即函数f (x)的零点个数为2.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·北京通州区期末)已知函数f (x)=若g(x)
=f (x)-a有3个零点,则a的取值范围为( )
A.(-1,0) B.
C. D.∪{-1}
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [设h(x)=(x>0),则h′(x)=,
令h′(x)>0,解得0<x<e,令h′(x)<0,解得x>e,
所以函数h(x)在(0,e)单调递增,在(e,+∞)单调递减.
所以h(x)max=.因为g(x)=f (x)-a=0,
所以f (x)=a有三个根.
作出函数y=f (x)和y=a的图象如图所示,
所以a的取值范围为.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·广东模拟)若函数f (x)=|2x-3|-1-m只有1个零点,则m的取值范围是_________________.
[2,+∞)∪{-1}
题号
1
3
5
2
4
6
8
7
9
10
11
12
[2,+∞)∪{-1} [由f (x)=|2x-3|-1-m=0,得|2x-3|-1=m.
设函数g(x)=|2x-3|-1=
作出g(x)的大致图象,如图所示.
由图可知,m的取值范围是[2,+∞)∪{-1}.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2025·天津红桥区模拟)对实数a和b,定义运算“ ”:a b=设函数f (x)=(x2-2) (x-x2),x∈R,若函数y=f (x)+c的图象与x轴恰有两个公共点,则实数c的取值范围是_________
____________.
∪
[2,+∞)
题号
1
3
5
2
4
6
8
7
9
10
11
12
∪[2,+∞) [∵a b=
∴函数f (x)=(x2-2) (x-x2)=
由图可知,当-c∈(-∞,-2],
即c∈∪[2,+∞)时,
函数f (x) 与y=-c的图象有两个公共点,
∴实数c的取值范围是∪[2,+∞).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2025·海南模拟)已知函数f (x)是定义域为R的奇函数,当x>0时,f (x)=x2-2x.
(1)求出函数f (x)在R上的解析式;
(2)画出函数f (x)的图象,并写出单调区间;
(3)若y=f (x)的图象与y=m有3个交点,求实数m的取值范围.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)①由于函数f (x)是定义域为R的奇函数,f (0)=0;
②当x<0时,-x>0,因为f (x)是奇函数,
所以f (-x)=-f (x).
所以f (x)=-f (-x)=-[(-x)2+2x]=-x2-2x,
综上,函数f (x)在R上的解析式为
f (x)=
(2)图象如图所示,
单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
(3)因为方程f (x)=m有三个不同的解,由图象可知,满足题意的m的取值范围为(-1,1).
谢 谢 !
同课章节目录
