《高考快车道》2026版高三一轮总复习数学(基础版)40 第四章 第5课时 三角函数的图象与性质 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)40 第四章 第5课时 三角函数的图象与性质 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:46 | ||
图片预览





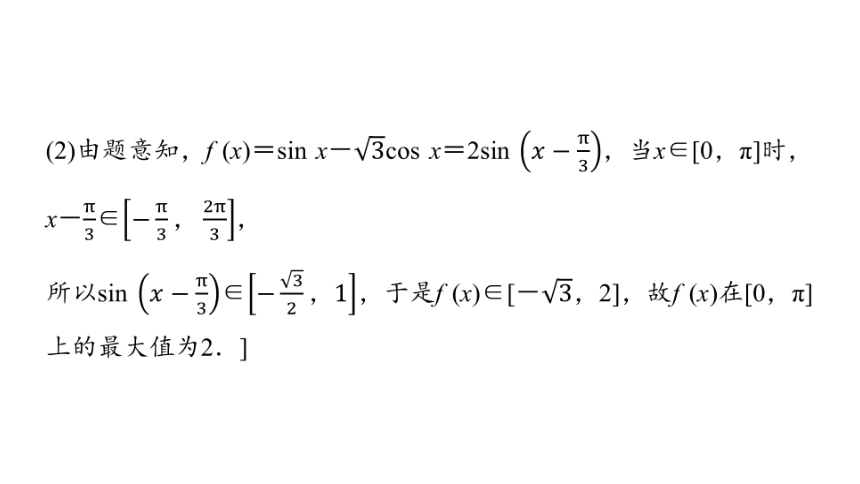




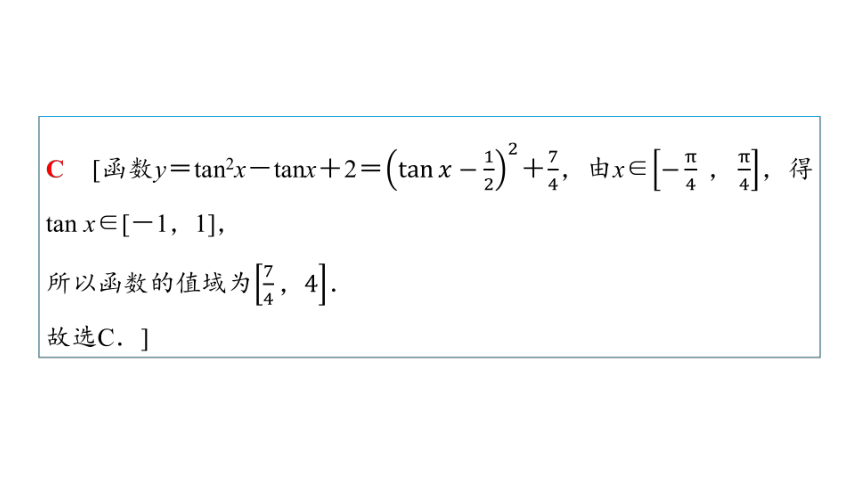
文档简介
(共85张PPT)
第四章 三角函数与解三角形
第5课时 三角函数的图象与性质
[考试要求] 1.能画出三角函数的图象.
2.了解三角函数的周期性、奇偶性、单调性、最大(小)值.
3.借助图象理解正弦函数、余弦函数在[0,2π]上,正切函数在上的性质.
考点一 三角函数的定义域和值域
1.用五点法作正弦函数和余弦函数的简图
正弦函数y=sin x,x∈[0,2π]图象的五个关键点是:(0,0),,(π,0),,(2π,0).
余弦函数y=cos x,x∈[0,2π]图象的五个关键点是:(0,1),,(π,-1),,(2π,1).
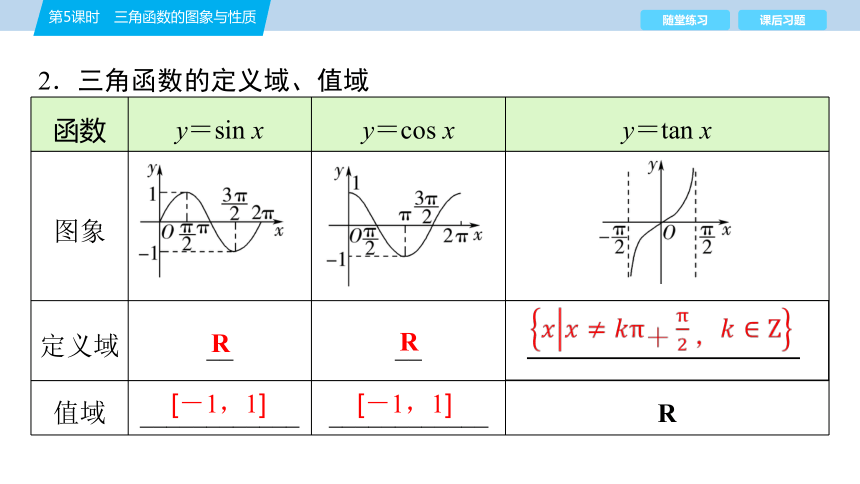
2.三角函数的定义域、值域
函数 y=sin x y=cos x y=tan x
图象
定义域 __ __
值域 ____________ ____________ R
R
R
[-1,1]
[-1,1]
[典例1] (1)(2025·上海市浦东新区模拟)函数f (x)=的定义域为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
√
(2)(2024·全国甲卷)函数f (x)=sin x-cos x在[0,π]上的最大值是________.
(1)B (2)2 [(1)由题意得,1-2cos x≥0,即cos x≤,
解得+2kπ≤x≤+2kπ,k∈Z,
所以函数f (x)=的定义域为,k∈Z.故选B.
2
(2)由题意知,f (x)=sin x-cos x=2sin ,当x∈[0,π]时,x-∈,
所以sin ∈,于是f (x)∈[-,2],故f (x)在[0,π]上的最大值为2.]
反思领悟 本例(1)由1-2cos x≥0得cos x≤后,借助余弦函数y=cos x的图象来求解,故要能借助“五点法”快速画出正弦(余弦)函数的简图;本例(2),把所给三角函数式变换成f (x)=2sin (一般形式f (x)=A sin (ωx+φ))的形式,把x-(一般形式ωx+φ)看作一个整体,利用y=sin x的单调性求值域.
巩固迁移1 (1)(2024·日照期末)函数y=(0≤x≤2π)的定义域为( )
A.B. C.D.
(2)(2024·广西期末)函数y=cos ,x∈的值域是( )
A. B.C. D.
√
√
(1)C (2)A [(1)由题意得2sin x-1≥0,即sin x≥,
因为0≤x≤2π,所以≤x≤.故选C.
(2)因为x∈,所以x+∈,
因为y=cos ,所以y∈,即y∈.故选A.]
【教用·备选题】
1.(2024·滨州高三入学考试)函数y=tan2x-tanx+2,x∈的值域为( )
A. B.
C. D.[2,4]
√
C [函数y=tan2x-tanx+2=+,由x∈,得tan x∈[-1,1],
所以函数的值域为.
故选C.]
2.函数y=sin x-cos x+sin x cos x的值域为_____________.
[设t=sin x-cos x,则t2=sin2x+cos2x-2sinx cos x,sin x cos x=,且-≤t≤.
∴y=-+t+=-(t-1)2+1.
当t=1时,ymax=1;
当t=-时,ymin=-.∴函数的值域为.]
考点二 三角函数的周期性、奇偶性、对称性
函数 y=sin x y=cos x y=tan x
图象
最小正 周期 2π ____ __
2π
π
函数 y=sin x y=cos x y=tan x
奇偶性 ______ ______ 奇函数
对称 中心 ______________(k∈Z) (k∈Z)
(k∈Z)
对称轴 方程 __________ (k∈Z) ________(k∈Z)
奇函数
偶函数
(kπ,0)
x=kπ+
x=kπ
[常用结论]
1.对称性与周期性
(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是个周期,相邻的对称中心与对称轴之间的距离是个周期.
(2)正切曲线相邻两对称中心之间的距离是个周期.
2.与三角函数的奇偶性相关的结论
(1)若y=A sin (ωx+φ)为偶函数,则φ=kπ+(k∈Z);若为奇函数,则φ=kπ(k∈Z).
(2)若y=A cos (ωx+φ)为偶函数,则φ=kπ(k∈Z);若为奇函数,则φ=kπ+(k∈Z).
(3)若y=A tan (ωx+φ)为奇函数,则φ=kπ(k∈Z).
考向1 三角函数的周期性
[典例2] (1)(2024·杭州期末)下列函数中,以π为最小正周期的奇函数是( )
A.y=sin 2x B.y=cos x C.y=2|sin x| D.y=2|cos x|
(2)(2024·驻马店期末)函数f (x)=2sin (ωx+φ)(ω>0,0<φ<π)的最小正周期为T,若f =1,则φ=( )
A. B. C. D.
√
√
(1)A (2)B [(1)由于y=sin 2x是最小正周期为π的奇函数,则A正确;
由于y=cos x为最小正周期为2π的偶函数,则B错误;
由于y=2|sin x|是最小正周期为π的偶函数,则C错误;
由于y=2|cos x|是最小正周期为π的偶函数,则D错误.故选A.
(2)因为函数f (x)=2sin (ωx+φ)(ω>0,0<φ<π)的最小正周期为T=,则f =1,即2sin =1,可得2sin =1,即2cos φ=1,则cos φ=,又0<φ<π,则φ=.故选B.]
反思领悟 本例(1)选项A,B和本例(2)可利用函数y=A sin (ωx+φ)或y=A cos (ωx+φ)的最小正周期T=来求;本例(1)选项C,D的周期可画出函数简图,通过观察其图象求得.
巩固迁移2 (1)(2025·八省联考)函数f (x)=cos 的最小正周期是( )
A.B. C.π D.2π
(2)(2024·北京东城区月考)在下列函数中,以π为最小正周期的是( )
A.y=tan 2x B.y=sin x cos x
C.y=|sin 2x| D.y=sin x+cos x
(3)函数f (x)=cos22024πx的最小正周期为________.
√
√
(1)D (2)B (3) [(1)由题意知,f (x)的最小正周期T=2π.故选D.
(2)对于A,函数y=tan 2x的最小正周期T=,故A错误;
对于B,函数y=sin x cos x=sin 2x,最小正周期T==π,故B正确;
对于C,=|sin (2x+π)|=|sin 2x|,
最小正周期T=,故C错误;
对于D,函数y=sin x+cos x=sin ,最小正周期T=2π,故D错误.故选B.
(3)因为f (x)=cos22 024πx=(cos 4 048πx+1)=cos 4 048πx+,
所以周期T==.]
考向2 三角函数的奇偶性与对称性
[典例3] (1)(2025·杭州模拟)设函数f (x)=2sin ,则下列叙述正确的是( )
A.f (x)的最小正周期为2π
B.f (x)的图象关于直线x=对称
C.f (x)在上的最小值为-
D.f (x)的图象关于点对称
√
(2)函数f (x)=3sin +1,φ∈(0,π),且f (x)为偶函数,则φ=________,f (x)图象的对称中心为__________________.
(1)C (2),k∈Z [(1)对于A,f (x)的最小正周期为=π,故A错误;
对于B,∵sin =-≠±1,故B错误;
对于C,当x∈时,2x-∈,
,k∈Z
∴sin ∈,
∴2sin ∈,
∴f (x)在上的最小值为-,故C正确;
对于D,∵f =2sin =,
∴f (x)的图象关于点对称,故D错误.故选C.
(2)若f (x)=3sin +1为偶函数,
则-+φ=kπ+,k∈Z,即φ=+kπ,k∈Z,
又∵φ∈(0,π),∴φ=.
∴f (x)=3sin +1=3cos 2x+1,
由2x=+kπ,k∈Z,得x=,k∈Z,
∴f (x)图象的对称中心为,k∈Z.]
反思领悟 (1)三角函数中奇函数一般可化为y=A sin ωx或y=
A tan ωx的形式,而偶函数一般可化为y=A cos ωx的形式.
(2)判断某一直线、某一点是否为y=A sin (ωx+φ)或y=A cos (ωx+φ)的对称轴、对称中心时,可根据对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点这一性质进行检验判断.
巩固迁移3 (1)(多选)已知函数f (x)=sin x(sin x-cos x),则下列说法正确的是( )
A.函数f (x)的最小正周期为π
B.点是y=f (x)图象的对称中心
C.点是y=f (x)图象的对称中心
D.直线x=是y=f (x)图象的对称轴
(2)已知函数f (x)=cos 是奇函数,且φ∈,则φ的值为________.
√
√
(1)AD (2) [(1)f (x)=sin x(sin x-cos x)
=sin2x-sinx cos x
=sin 2x
=-sin ,
T==π,故A正确;
当x=-时,2x+=0,
此时sin =0,
则函数的图象关于点对称,
故B错误;
当x=时,2x+=,
此时sin =1,
则函数的图象关于直线x=对称,故C错误;
当x=时,2x+=,此时sin =-1,
则函数的图象关于直线x=对称,故D正确.
(2)由已知,得+φ=kπ+(k∈Z),
所以φ=kπ+(k∈Z),
又因为φ∈,
所以当k=0时,φ=符合题意.]
考点三 三角函数的单调性
函数 y=sin x y=cos x y=tan x
图象
函数 y=sin x y=cos x y=tan x
单调 递增 区间 (k∈Z) ____________ (k∈Z) (k∈Z)
单调 递减 区间 (k∈Z) _____________ (k∈Z)
[2kπ-π,2kπ]
[2kπ,2kπ+π]
[典例4] (2025·湛江模拟)函数y=3-2cos 的单调递增区间是( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
√
B [由题意得y=3-2cos
=3-2cos =3-2cos ,
要求函数的单调递增区间,即求y=cos 的单调递减区间,
当2kπ≤2x+≤π+2kπ,k∈Z,即kπ-≤x≤+kπ,k∈Z时,
y=cos 单调递减,即y=3-2cos 单调递增,故B正确.
故选B.]
反思领悟 本例求单调递增区间的关键是利用诱导公式将函数化为y=3-2cos 后,将“2x+”视为一个整体解不等式.
巩固迁移4 (人教A版必修第一册P214习题5.4T14改编)下列区间中,函数f (x)=1-sin 单调递增的区间是( )
A. B.
C. D.
√
A [函数f (x)=1-sin =sin +1,
要求函数的单调递增区间,即-+2kπ≤x-+2kπ(k∈Z),
即-+2kπ≤x≤+2kπ(k∈Z).
令k=0,得到-≤x≤,则A正确,B错误;
令k=1,得到≤x≤,则C,D错误.故选A.]
解析式中含三角函数绝对值的函数性质问题,求解的主要方法是根据函数的有关性质(如奇偶性、周期性、对称性等),研究函数的值域(最值)、单调性、零点个数等,需要去掉绝对值符号,结合所得函数解析式的特征求解.
定义法研究三角函数性质的方法:不能化为形如f (x)= A sin (ωx+φ)或f (x)=A cos (ωx+φ)(Aω≠0)的函数的性质问题,可借助定义求解,其依据是:(1)若存在非零常数T,满足f (x+T)=f (x),则函数是周期为T的函数;(2)若函数满足f (x)=f (2a-x),则图象关于直线x=a对称;(3)若函数满足f (x)+f (2a-x)=2b,则函数图象关于点(a,b)对称;(4)利用奇偶性的定义判断函数奇偶性.
[典例] (多选)(2025·六安金安区模拟)已知函数f (x)=|sin x+cos x|+|sin x-cos x|,则下列关于函数f (x)的说法,正确的是( )
A.f (x)的一个周期为
B.f (x)的图象关于直线x=对称
C.f (x)在上单调递增
D.f (x)的值域为[,2]
√
√
√
ABD [对于A,f=
=|cos x-sin x|+|cos x+sin x|=f (x),
因此f (x)的一个周期是,故A正确;
对于B,f (π-x)=|sin (π-x)+cos (π-x)|+|sin (π-x)-cos (π-x)|
=|sin x-cos x|+|sin x+cos x|=f (x),
因此,直线x=是函数f (x)图象的一条对称轴,故B正确;
对于C,由于f (0)=2,f =,可知f (0)>f ,所以f (x)不可能在上单调递增,故C错误;
对于D,对于区间,其区间长度恰好等于f (x)的周期,
可知f (x)在R上的值域与它在上的值域相同,
当x∈时,f (x)=sin x+cos x+cos x-sin x=2cos x,
由y=cos x在区间上的值域为,可知f (x)在区间上的值域为[,2],因此,f (x)在R上的值域为[,2],故D正确.故选ABD.]
应用体验 (多选)(2024·烟台二模)已知函数f (x)=sin x·|cos x|,则
( )
A.f (x)是奇函数
B.f (x)的最小正周期为π
C.f (x)的最小值为-
D.f (x)在上单调递增
√
√
AC [f (x)=sin x·|cos x|
=k∈Z,
其大致图象如图所示,
因为f (-x)=sin (-x)|cos (-x)|=-sin x|cos x|=-f (x),即f (x)为奇函数,A正确;
因为f (x+π)=sin (x+π)|cos (x+π)|=-sin x·|cos x|≠f (x),即π不是
f (x)的最小正周期,B错误;
结合函数图象可知,f (x)的最小值为-,C正确;
函数f (x)在上不单调,D错误.故选AC.]
随堂练习
√
1.(2024·日照期末)函数y=cos 的最小正周期是( )
A.π B.2π
C.1 D.2
D [y=cos 的最小正周期为T==2.故选D.]
2.(2024·上海宝山区校级期中)函数y=1+cos x(x∈[0,2π])的简图是( )
√
A B
C D
D [函数y=cos x,x∈[0,2π]的图象如图所示:
将函数y=cos x,x∈[0,2π]的图象向上平移1个单位长度得到y=1+cos x(x∈[0,2π])的简图,
如图所示.
故选D.]
3.(2024·焦作博爱县月考)函数f (x)=sin ·cos 是
( )
A.最小正周期为π的奇函数
B.最小正周期为π的偶函数
C.最小正周期为2π的非奇非偶函数
D.最小正周期为π的非奇非偶函数
√
D [f (x)=sin cos =sin ·sin =sin2=,
所以函数f (x)为最小正周期为π的非奇非偶函数.故选D.]
4.若函数y=cos 的单调递减区间为M,y=cos (2π-x)的单调递减区间为N,则M∩N=____________________.
(k∈Z) [因为y=cos =-sin x,所以函数y=cos 的单调递减区间为(k∈Z).又y=
cos (2π-x)=cos x,所以函数y=cos (2π-x)的单调递减区间为[2kπ,2kπ+π](k∈Z),所以所求交集为两个区间的公共部分,即(k∈Z).]
(k∈Z)
【教用·备选题】
1.(2024·南通四模)下列函数中,以π为周期,且其图象关于点对称的是( )
A.y=tan x B.y=|sin x|
C.y=2cos2x-1 D.y=sinx-cos x
√
C [根据正切函数的性质可知,y=tan x的图象不关于点对称,A不符合题意;
根据正弦函数性质及函数图象变换可知,y=|sin x|的图象不关于点对称,B不符合题意;
y=2cos2x-1=cos2x以π为周期,且其图象关于点对称,C符合题意;
y=sin x-cos x=sin 的周期为2π,D不符合题意.
故选C.]
2.(2024·普洱期末)函数f (x)=2cos2x+3sinx在上的值域为
( )
A.[3,4] B.
C. D.
√
B [依题意,f (x)=-2sin2x+3sinx+2,令sin x=t,
因为≤x≤,所以≤t≤1,
故y=-2t2+3t+2,t∈.
故当t=时,y有最大值,当t=1时,y有最小值3,
故所求值域为.
故选B.]
3.(2025·武威市凉州区模拟)已知函数f (x)=cos x sin x-cos2x+,x∈R.
(1)求f (x)的最小正周期;
(2)求f (x)在区间上的最大值和最小值.
[解] (1)f (x)=cosx sin x-cos2x+
=sinx cos x-(2cos2x-1)
=sin2x-cos 2x=sin .
∴f (x)的最小正周期T==π.
(2)∵-≤x≤,∴-≤2x-,
不妨设z=2x-,因为y=sin z在区间上单调递减,在区间上单调递增,故z=-时,函数取得最小值-1,此时x=-.
又因为sin =>sin =-,故z=时函数取得最大值,此时x=.
故函数f (x)在区间上的最大值为,最小值为-1.
课后习题(二十八) 三角函数的图象与性质
1.(人教A版必修第一册P207练习T3改编)下列关于函数y=4sin x,x∈
[-π,π]的单调性的叙述,正确的是( )
A.在[-π,0]上单调递增,在[0,π]上单调递减
B.在上单调递增,在和上单调递减
C.在[0,π]上单调递增,在[-π,0]上单调递减
D.在和上单调递增,在上单调递减
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [函数y=4sin x在和上单调递减,在上单调递增.故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(多选)(人教A版必修第一册P203练习T2改编)下列函数中,最小正周期为π,且图象关于直线x=对称的函数是( )
A.y=cos
B.y=2sin
C.y=sin
D.y=2cos
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AB [选项C中,函数y=sin 的最小正周期T==4π,故排除C;将x=依次代入选项A,B,D中的解析式,求得函数值分别为-,2,1,故A,B正确,D错误.故选AB.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(多选)(人教B版必修第三册P59练习BT5改编)已知函数f (x)=
tan ,下列结论正确的是( )
A.函数f (x)的最小正周期为
B.函数f (x)的定义域为
C.函数f (x)图象的对称中心为,k∈Z
D.函数f (x)的单调递增区间为,k∈Z
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ACD [对于A,函数f (x)=tan 的最小正周期T=,所以A正确;对于B,令2x-≠+kπ,k∈Z,得x≠,k∈Z,即函数f (x)的定义域为,所以B错误;对于C,令2x-=,k∈Z,解得x=,k∈Z,所以函数f (x)的图象关于点,k∈Z对称,所以C正确;对于D,令kπ-<2x-故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版必修第一册P205例3改编)函数y=3-2cos的最大值为________,此时x=_____________.
5 +2kπ(k∈Z) [函数y=3-2cos的最大值为3+2=5,此时x+=π+2kπ,k∈Z,即x=+2kπ(k∈Z).]
5
+2kπ(k∈Z)
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·上海静安区二模)函数y=2sin x-cos x(x∈R)的最小正周期为( )
A.2π B.π
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [因为y=2sin x-cos x=
=sin (x-φ),tan φ=,根据周期公式可得T=2π.
故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·泉州鲤城区期末)已知函数f (x)=sin (ω>0)的最小正周期为π,则函数在区间上的最大值是( )
A.0 B.
C. D.1
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [f (x)=sin ,由T==π,得ω=2,
即f (x)=sin ,当x∈时,2x+∈,
所以f (x)∈,从而f (x)max=f =1.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·深圳宝安区期末)已知函数f (x)=sin (ω>0)的最小正周期为π,则该函数的图象( )
A.关于点对称
B.关于直线x=对称
C.关于点对称
D.关于直线x=对称
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [∵函数f (x)=sin (ω>0)的最小正周期为π,∴ω=2,即f (x)=sin ,则令2x+=kπ,解得x=-,k∈Z,∴f (x)图象的对称中心为(k∈Z),则当k=1时,图象的对称中心为,故A正确,C错误;
令2x+=kπ+,解得x=,k∈Z,∴f (x)图象的对称轴为直线x=,k∈Z,故B,D错误,故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·西安碑林区期末)已知函数f (x)=cos (x∈R),下列结论错误的是( )
A.函数f (x)的最小正周期为π
B.函数f (x)的图象关于点对称
C.函数f (x)在区间上单调递减
D.函数f (x)的图象关于直线x=对称
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
BC [因为f (x)=cos ,
所以f (x)的最小正周期为T==π,故A正确;
f =cos =cos =-cos =-,
f ≠0,则f (x)的图象不关于点对称,故B错误;
当x∈时,2x-∈,
又y=cos x在上不单调,
所以函数f (x)在区间上不单调递减,故C错误;
当x=时,f =cos =,为最大值,
所以f (x)的图象关于直线x=对称,故D正确.
故选BC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·北京朝阳区期末)函数f (x)=3cos -2图象的一个对称中心为( )
A. B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [f (x)=3cos -2=3cos -2,
函数f (x)图象的对称中心满足2x-=kπ+,k∈Z,即x=kπ+,k∈Z,
所以函数f (x)图象的对称中心为,k∈Z,
当k=0时,为函数f (x)图象的一个对称中心.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·宜宾长宁区期末)已知函数y=sin (2x+2φ)(φ>0)是偶函数,则φ的最小值是________.
[函数y=sin (2x+2φ)(φ>0)是偶函数,则2φ=kπ+(k∈Z),
解得φ=(k∈Z),当k=0时,φ的最小值为.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2025·北京西城区模拟)已知函数f (x)=sin 2x+cos 2x.
(1)求f (0);
(2)求函数f (x)的最小正周期及对称轴方程;
(3)求函数f (x)的单调递增区间.
[解] (1)f (x)=sin 2x+cos 2x=sin ,则f (0)=1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)函数f (x)的最小正周期为π.
令2x+=+kπ,k∈Z,则x=,k∈Z,
即对称轴方程为x=,k∈Z.
(3)令-+2kπ≤2x++2kπ,k∈Z,
解得-+kπ≤x≤+kπ,k∈Z,
故函数f (x)的单调递增区间为
,k∈Z.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·海口期末)已知函数f (x)=2sin (0<ω<3),直线x=是函数f (x)图象的一条对称轴.
(1)求函数f (x)的最小正周期和单调递增区间;
(2)若x∈,求函数f (x)的值域.
[解] (1)根据题意可得ω·=+kπ,k∈Z,所以ω=2+3k,k∈Z,
又0<ω<3,所以ω=2,所以函数f (x)的最小正周期为==π.
因为f (x)=2sin ,令-+2kπ≤2x-+2kπ,k∈Z,
所以-+kπ≤x≤+kπ,k∈Z,
所以函数f (x)的单调递增区间为,k∈Z.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)因为x∈,
所以2x-∈,
所以sin ∈,
所以2sin ∈[-1,2],
所以函数f (x)的值域为[-1,2].
谢 谢 !
第四章 三角函数与解三角形
第5课时 三角函数的图象与性质
[考试要求] 1.能画出三角函数的图象.
2.了解三角函数的周期性、奇偶性、单调性、最大(小)值.
3.借助图象理解正弦函数、余弦函数在[0,2π]上,正切函数在上的性质.
考点一 三角函数的定义域和值域
1.用五点法作正弦函数和余弦函数的简图
正弦函数y=sin x,x∈[0,2π]图象的五个关键点是:(0,0),,(π,0),,(2π,0).
余弦函数y=cos x,x∈[0,2π]图象的五个关键点是:(0,1),,(π,-1),,(2π,1).
2.三角函数的定义域、值域
函数 y=sin x y=cos x y=tan x
图象
定义域 __ __
值域 ____________ ____________ R
R
R
[-1,1]
[-1,1]
[典例1] (1)(2025·上海市浦东新区模拟)函数f (x)=的定义域为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
√
(2)(2024·全国甲卷)函数f (x)=sin x-cos x在[0,π]上的最大值是________.
(1)B (2)2 [(1)由题意得,1-2cos x≥0,即cos x≤,
解得+2kπ≤x≤+2kπ,k∈Z,
所以函数f (x)=的定义域为,k∈Z.故选B.
2
(2)由题意知,f (x)=sin x-cos x=2sin ,当x∈[0,π]时,x-∈,
所以sin ∈,于是f (x)∈[-,2],故f (x)在[0,π]上的最大值为2.]
反思领悟 本例(1)由1-2cos x≥0得cos x≤后,借助余弦函数y=cos x的图象来求解,故要能借助“五点法”快速画出正弦(余弦)函数的简图;本例(2),把所给三角函数式变换成f (x)=2sin (一般形式f (x)=A sin (ωx+φ))的形式,把x-(一般形式ωx+φ)看作一个整体,利用y=sin x的单调性求值域.
巩固迁移1 (1)(2024·日照期末)函数y=(0≤x≤2π)的定义域为( )
A.B. C.D.
(2)(2024·广西期末)函数y=cos ,x∈的值域是( )
A. B.C. D.
√
√
(1)C (2)A [(1)由题意得2sin x-1≥0,即sin x≥,
因为0≤x≤2π,所以≤x≤.故选C.
(2)因为x∈,所以x+∈,
因为y=cos ,所以y∈,即y∈.故选A.]
【教用·备选题】
1.(2024·滨州高三入学考试)函数y=tan2x-tanx+2,x∈的值域为( )
A. B.
C. D.[2,4]
√
C [函数y=tan2x-tanx+2=+,由x∈,得tan x∈[-1,1],
所以函数的值域为.
故选C.]
2.函数y=sin x-cos x+sin x cos x的值域为_____________.
[设t=sin x-cos x,则t2=sin2x+cos2x-2sinx cos x,sin x cos x=,且-≤t≤.
∴y=-+t+=-(t-1)2+1.
当t=1时,ymax=1;
当t=-时,ymin=-.∴函数的值域为.]
考点二 三角函数的周期性、奇偶性、对称性
函数 y=sin x y=cos x y=tan x
图象
最小正 周期 2π ____ __
2π
π
函数 y=sin x y=cos x y=tan x
奇偶性 ______ ______ 奇函数
对称 中心 ______________(k∈Z) (k∈Z)
(k∈Z)
对称轴 方程 __________ (k∈Z) ________(k∈Z)
奇函数
偶函数
(kπ,0)
x=kπ+
x=kπ
[常用结论]
1.对称性与周期性
(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是个周期,相邻的对称中心与对称轴之间的距离是个周期.
(2)正切曲线相邻两对称中心之间的距离是个周期.
2.与三角函数的奇偶性相关的结论
(1)若y=A sin (ωx+φ)为偶函数,则φ=kπ+(k∈Z);若为奇函数,则φ=kπ(k∈Z).
(2)若y=A cos (ωx+φ)为偶函数,则φ=kπ(k∈Z);若为奇函数,则φ=kπ+(k∈Z).
(3)若y=A tan (ωx+φ)为奇函数,则φ=kπ(k∈Z).
考向1 三角函数的周期性
[典例2] (1)(2024·杭州期末)下列函数中,以π为最小正周期的奇函数是( )
A.y=sin 2x B.y=cos x C.y=2|sin x| D.y=2|cos x|
(2)(2024·驻马店期末)函数f (x)=2sin (ωx+φ)(ω>0,0<φ<π)的最小正周期为T,若f =1,则φ=( )
A. B. C. D.
√
√
(1)A (2)B [(1)由于y=sin 2x是最小正周期为π的奇函数,则A正确;
由于y=cos x为最小正周期为2π的偶函数,则B错误;
由于y=2|sin x|是最小正周期为π的偶函数,则C错误;
由于y=2|cos x|是最小正周期为π的偶函数,则D错误.故选A.
(2)因为函数f (x)=2sin (ωx+φ)(ω>0,0<φ<π)的最小正周期为T=,则f =1,即2sin =1,可得2sin =1,即2cos φ=1,则cos φ=,又0<φ<π,则φ=.故选B.]
反思领悟 本例(1)选项A,B和本例(2)可利用函数y=A sin (ωx+φ)或y=A cos (ωx+φ)的最小正周期T=来求;本例(1)选项C,D的周期可画出函数简图,通过观察其图象求得.
巩固迁移2 (1)(2025·八省联考)函数f (x)=cos 的最小正周期是( )
A.B. C.π D.2π
(2)(2024·北京东城区月考)在下列函数中,以π为最小正周期的是( )
A.y=tan 2x B.y=sin x cos x
C.y=|sin 2x| D.y=sin x+cos x
(3)函数f (x)=cos22024πx的最小正周期为________.
√
√
(1)D (2)B (3) [(1)由题意知,f (x)的最小正周期T=2π.故选D.
(2)对于A,函数y=tan 2x的最小正周期T=,故A错误;
对于B,函数y=sin x cos x=sin 2x,最小正周期T==π,故B正确;
对于C,=|sin (2x+π)|=|sin 2x|,
最小正周期T=,故C错误;
对于D,函数y=sin x+cos x=sin ,最小正周期T=2π,故D错误.故选B.
(3)因为f (x)=cos22 024πx=(cos 4 048πx+1)=cos 4 048πx+,
所以周期T==.]
考向2 三角函数的奇偶性与对称性
[典例3] (1)(2025·杭州模拟)设函数f (x)=2sin ,则下列叙述正确的是( )
A.f (x)的最小正周期为2π
B.f (x)的图象关于直线x=对称
C.f (x)在上的最小值为-
D.f (x)的图象关于点对称
√
(2)函数f (x)=3sin +1,φ∈(0,π),且f (x)为偶函数,则φ=________,f (x)图象的对称中心为__________________.
(1)C (2),k∈Z [(1)对于A,f (x)的最小正周期为=π,故A错误;
对于B,∵sin =-≠±1,故B错误;
对于C,当x∈时,2x-∈,
,k∈Z
∴sin ∈,
∴2sin ∈,
∴f (x)在上的最小值为-,故C正确;
对于D,∵f =2sin =,
∴f (x)的图象关于点对称,故D错误.故选C.
(2)若f (x)=3sin +1为偶函数,
则-+φ=kπ+,k∈Z,即φ=+kπ,k∈Z,
又∵φ∈(0,π),∴φ=.
∴f (x)=3sin +1=3cos 2x+1,
由2x=+kπ,k∈Z,得x=,k∈Z,
∴f (x)图象的对称中心为,k∈Z.]
反思领悟 (1)三角函数中奇函数一般可化为y=A sin ωx或y=
A tan ωx的形式,而偶函数一般可化为y=A cos ωx的形式.
(2)判断某一直线、某一点是否为y=A sin (ωx+φ)或y=A cos (ωx+φ)的对称轴、对称中心时,可根据对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点这一性质进行检验判断.
巩固迁移3 (1)(多选)已知函数f (x)=sin x(sin x-cos x),则下列说法正确的是( )
A.函数f (x)的最小正周期为π
B.点是y=f (x)图象的对称中心
C.点是y=f (x)图象的对称中心
D.直线x=是y=f (x)图象的对称轴
(2)已知函数f (x)=cos 是奇函数,且φ∈,则φ的值为________.
√
√
(1)AD (2) [(1)f (x)=sin x(sin x-cos x)
=sin2x-sinx cos x
=sin 2x
=-sin ,
T==π,故A正确;
当x=-时,2x+=0,
此时sin =0,
则函数的图象关于点对称,
故B错误;
当x=时,2x+=,
此时sin =1,
则函数的图象关于直线x=对称,故C错误;
当x=时,2x+=,此时sin =-1,
则函数的图象关于直线x=对称,故D正确.
(2)由已知,得+φ=kπ+(k∈Z),
所以φ=kπ+(k∈Z),
又因为φ∈,
所以当k=0时,φ=符合题意.]
考点三 三角函数的单调性
函数 y=sin x y=cos x y=tan x
图象
函数 y=sin x y=cos x y=tan x
单调 递增 区间 (k∈Z) ____________ (k∈Z) (k∈Z)
单调 递减 区间 (k∈Z) _____________ (k∈Z)
[2kπ-π,2kπ]
[2kπ,2kπ+π]
[典例4] (2025·湛江模拟)函数y=3-2cos 的单调递增区间是( )
A.(k∈Z)
B.(k∈Z)
C.(k∈Z)
D.(k∈Z)
√
B [由题意得y=3-2cos
=3-2cos =3-2cos ,
要求函数的单调递增区间,即求y=cos 的单调递减区间,
当2kπ≤2x+≤π+2kπ,k∈Z,即kπ-≤x≤+kπ,k∈Z时,
y=cos 单调递减,即y=3-2cos 单调递增,故B正确.
故选B.]
反思领悟 本例求单调递增区间的关键是利用诱导公式将函数化为y=3-2cos 后,将“2x+”视为一个整体解不等式.
巩固迁移4 (人教A版必修第一册P214习题5.4T14改编)下列区间中,函数f (x)=1-sin 单调递增的区间是( )
A. B.
C. D.
√
A [函数f (x)=1-sin =sin +1,
要求函数的单调递增区间,即-+2kπ≤x-+2kπ(k∈Z),
即-+2kπ≤x≤+2kπ(k∈Z).
令k=0,得到-≤x≤,则A正确,B错误;
令k=1,得到≤x≤,则C,D错误.故选A.]
解析式中含三角函数绝对值的函数性质问题,求解的主要方法是根据函数的有关性质(如奇偶性、周期性、对称性等),研究函数的值域(最值)、单调性、零点个数等,需要去掉绝对值符号,结合所得函数解析式的特征求解.
定义法研究三角函数性质的方法:不能化为形如f (x)= A sin (ωx+φ)或f (x)=A cos (ωx+φ)(Aω≠0)的函数的性质问题,可借助定义求解,其依据是:(1)若存在非零常数T,满足f (x+T)=f (x),则函数是周期为T的函数;(2)若函数满足f (x)=f (2a-x),则图象关于直线x=a对称;(3)若函数满足f (x)+f (2a-x)=2b,则函数图象关于点(a,b)对称;(4)利用奇偶性的定义判断函数奇偶性.
[典例] (多选)(2025·六安金安区模拟)已知函数f (x)=|sin x+cos x|+|sin x-cos x|,则下列关于函数f (x)的说法,正确的是( )
A.f (x)的一个周期为
B.f (x)的图象关于直线x=对称
C.f (x)在上单调递增
D.f (x)的值域为[,2]
√
√
√
ABD [对于A,f=
=|cos x-sin x|+|cos x+sin x|=f (x),
因此f (x)的一个周期是,故A正确;
对于B,f (π-x)=|sin (π-x)+cos (π-x)|+|sin (π-x)-cos (π-x)|
=|sin x-cos x|+|sin x+cos x|=f (x),
因此,直线x=是函数f (x)图象的一条对称轴,故B正确;
对于C,由于f (0)=2,f =,可知f (0)>f ,所以f (x)不可能在上单调递增,故C错误;
对于D,对于区间,其区间长度恰好等于f (x)的周期,
可知f (x)在R上的值域与它在上的值域相同,
当x∈时,f (x)=sin x+cos x+cos x-sin x=2cos x,
由y=cos x在区间上的值域为,可知f (x)在区间上的值域为[,2],因此,f (x)在R上的值域为[,2],故D正确.故选ABD.]
应用体验 (多选)(2024·烟台二模)已知函数f (x)=sin x·|cos x|,则
( )
A.f (x)是奇函数
B.f (x)的最小正周期为π
C.f (x)的最小值为-
D.f (x)在上单调递增
√
√
AC [f (x)=sin x·|cos x|
=k∈Z,
其大致图象如图所示,
因为f (-x)=sin (-x)|cos (-x)|=-sin x|cos x|=-f (x),即f (x)为奇函数,A正确;
因为f (x+π)=sin (x+π)|cos (x+π)|=-sin x·|cos x|≠f (x),即π不是
f (x)的最小正周期,B错误;
结合函数图象可知,f (x)的最小值为-,C正确;
函数f (x)在上不单调,D错误.故选AC.]
随堂练习
√
1.(2024·日照期末)函数y=cos 的最小正周期是( )
A.π B.2π
C.1 D.2
D [y=cos 的最小正周期为T==2.故选D.]
2.(2024·上海宝山区校级期中)函数y=1+cos x(x∈[0,2π])的简图是( )
√
A B
C D
D [函数y=cos x,x∈[0,2π]的图象如图所示:
将函数y=cos x,x∈[0,2π]的图象向上平移1个单位长度得到y=1+cos x(x∈[0,2π])的简图,
如图所示.
故选D.]
3.(2024·焦作博爱县月考)函数f (x)=sin ·cos 是
( )
A.最小正周期为π的奇函数
B.最小正周期为π的偶函数
C.最小正周期为2π的非奇非偶函数
D.最小正周期为π的非奇非偶函数
√
D [f (x)=sin cos =sin ·sin =sin2=,
所以函数f (x)为最小正周期为π的非奇非偶函数.故选D.]
4.若函数y=cos 的单调递减区间为M,y=cos (2π-x)的单调递减区间为N,则M∩N=____________________.
(k∈Z) [因为y=cos =-sin x,所以函数y=cos 的单调递减区间为(k∈Z).又y=
cos (2π-x)=cos x,所以函数y=cos (2π-x)的单调递减区间为[2kπ,2kπ+π](k∈Z),所以所求交集为两个区间的公共部分,即(k∈Z).]
(k∈Z)
【教用·备选题】
1.(2024·南通四模)下列函数中,以π为周期,且其图象关于点对称的是( )
A.y=tan x B.y=|sin x|
C.y=2cos2x-1 D.y=sinx-cos x
√
C [根据正切函数的性质可知,y=tan x的图象不关于点对称,A不符合题意;
根据正弦函数性质及函数图象变换可知,y=|sin x|的图象不关于点对称,B不符合题意;
y=2cos2x-1=cos2x以π为周期,且其图象关于点对称,C符合题意;
y=sin x-cos x=sin 的周期为2π,D不符合题意.
故选C.]
2.(2024·普洱期末)函数f (x)=2cos2x+3sinx在上的值域为
( )
A.[3,4] B.
C. D.
√
B [依题意,f (x)=-2sin2x+3sinx+2,令sin x=t,
因为≤x≤,所以≤t≤1,
故y=-2t2+3t+2,t∈.
故当t=时,y有最大值,当t=1时,y有最小值3,
故所求值域为.
故选B.]
3.(2025·武威市凉州区模拟)已知函数f (x)=cos x sin x-cos2x+,x∈R.
(1)求f (x)的最小正周期;
(2)求f (x)在区间上的最大值和最小值.
[解] (1)f (x)=cosx sin x-cos2x+
=sinx cos x-(2cos2x-1)
=sin2x-cos 2x=sin .
∴f (x)的最小正周期T==π.
(2)∵-≤x≤,∴-≤2x-,
不妨设z=2x-,因为y=sin z在区间上单调递减,在区间上单调递增,故z=-时,函数取得最小值-1,此时x=-.
又因为sin =>sin =-,故z=时函数取得最大值,此时x=.
故函数f (x)在区间上的最大值为,最小值为-1.
课后习题(二十八) 三角函数的图象与性质
1.(人教A版必修第一册P207练习T3改编)下列关于函数y=4sin x,x∈
[-π,π]的单调性的叙述,正确的是( )
A.在[-π,0]上单调递增,在[0,π]上单调递减
B.在上单调递增,在和上单调递减
C.在[0,π]上单调递增,在[-π,0]上单调递减
D.在和上单调递增,在上单调递减
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [函数y=4sin x在和上单调递减,在上单调递增.故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(多选)(人教A版必修第一册P203练习T2改编)下列函数中,最小正周期为π,且图象关于直线x=对称的函数是( )
A.y=cos
B.y=2sin
C.y=sin
D.y=2cos
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AB [选项C中,函数y=sin 的最小正周期T==4π,故排除C;将x=依次代入选项A,B,D中的解析式,求得函数值分别为-,2,1,故A,B正确,D错误.故选AB.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(多选)(人教B版必修第三册P59练习BT5改编)已知函数f (x)=
tan ,下列结论正确的是( )
A.函数f (x)的最小正周期为
B.函数f (x)的定义域为
C.函数f (x)图象的对称中心为,k∈Z
D.函数f (x)的单调递增区间为,k∈Z
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ACD [对于A,函数f (x)=tan 的最小正周期T=,所以A正确;对于B,令2x-≠+kπ,k∈Z,得x≠,k∈Z,即函数f (x)的定义域为,所以B错误;对于C,令2x-=,k∈Z,解得x=,k∈Z,所以函数f (x)的图象关于点,k∈Z对称,所以C正确;对于D,令kπ-<2x-
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版必修第一册P205例3改编)函数y=3-2cos的最大值为________,此时x=_____________.
5 +2kπ(k∈Z) [函数y=3-2cos的最大值为3+2=5,此时x+=π+2kπ,k∈Z,即x=+2kπ(k∈Z).]
5
+2kπ(k∈Z)
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·上海静安区二模)函数y=2sin x-cos x(x∈R)的最小正周期为( )
A.2π B.π
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [因为y=2sin x-cos x=
=sin (x-φ),tan φ=,根据周期公式可得T=2π.
故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·泉州鲤城区期末)已知函数f (x)=sin (ω>0)的最小正周期为π,则函数在区间上的最大值是( )
A.0 B.
C. D.1
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [f (x)=sin ,由T==π,得ω=2,
即f (x)=sin ,当x∈时,2x+∈,
所以f (x)∈,从而f (x)max=f =1.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·深圳宝安区期末)已知函数f (x)=sin (ω>0)的最小正周期为π,则该函数的图象( )
A.关于点对称
B.关于直线x=对称
C.关于点对称
D.关于直线x=对称
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [∵函数f (x)=sin (ω>0)的最小正周期为π,∴ω=2,即f (x)=sin ,则令2x+=kπ,解得x=-,k∈Z,∴f (x)图象的对称中心为(k∈Z),则当k=1时,图象的对称中心为,故A正确,C错误;
令2x+=kπ+,解得x=,k∈Z,∴f (x)图象的对称轴为直线x=,k∈Z,故B,D错误,故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·西安碑林区期末)已知函数f (x)=cos (x∈R),下列结论错误的是( )
A.函数f (x)的最小正周期为π
B.函数f (x)的图象关于点对称
C.函数f (x)在区间上单调递减
D.函数f (x)的图象关于直线x=对称
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
BC [因为f (x)=cos ,
所以f (x)的最小正周期为T==π,故A正确;
f =cos =cos =-cos =-,
f ≠0,则f (x)的图象不关于点对称,故B错误;
当x∈时,2x-∈,
又y=cos x在上不单调,
所以函数f (x)在区间上不单调递减,故C错误;
当x=时,f =cos =,为最大值,
所以f (x)的图象关于直线x=对称,故D正确.
故选BC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·北京朝阳区期末)函数f (x)=3cos -2图象的一个对称中心为( )
A. B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [f (x)=3cos -2=3cos -2,
函数f (x)图象的对称中心满足2x-=kπ+,k∈Z,即x=kπ+,k∈Z,
所以函数f (x)图象的对称中心为,k∈Z,
当k=0时,为函数f (x)图象的一个对称中心.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·宜宾长宁区期末)已知函数y=sin (2x+2φ)(φ>0)是偶函数,则φ的最小值是________.
[函数y=sin (2x+2φ)(φ>0)是偶函数,则2φ=kπ+(k∈Z),
解得φ=(k∈Z),当k=0时,φ的最小值为.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2025·北京西城区模拟)已知函数f (x)=sin 2x+cos 2x.
(1)求f (0);
(2)求函数f (x)的最小正周期及对称轴方程;
(3)求函数f (x)的单调递增区间.
[解] (1)f (x)=sin 2x+cos 2x=sin ,则f (0)=1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)函数f (x)的最小正周期为π.
令2x+=+kπ,k∈Z,则x=,k∈Z,
即对称轴方程为x=,k∈Z.
(3)令-+2kπ≤2x++2kπ,k∈Z,
解得-+kπ≤x≤+kπ,k∈Z,
故函数f (x)的单调递增区间为
,k∈Z.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·海口期末)已知函数f (x)=2sin (0<ω<3),直线x=是函数f (x)图象的一条对称轴.
(1)求函数f (x)的最小正周期和单调递增区间;
(2)若x∈,求函数f (x)的值域.
[解] (1)根据题意可得ω·=+kπ,k∈Z,所以ω=2+3k,k∈Z,
又0<ω<3,所以ω=2,所以函数f (x)的最小正周期为==π.
因为f (x)=2sin ,令-+2kπ≤2x-+2kπ,k∈Z,
所以-+kπ≤x≤+kπ,k∈Z,
所以函数f (x)的单调递增区间为,k∈Z.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)因为x∈,
所以2x-∈,
所以sin ∈,
所以2sin ∈[-1,2],
所以函数f (x)的值域为[-1,2].
谢 谢 !
同课章节目录
