《高考快车道》2026版高三一轮总复习数学(基础版)48 第四章 阶段提能(八) 解三角形 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)48 第四章 阶段提能(八) 解三角形 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:46 | ||
图片预览









文档简介
(共35张PPT)
第四章 三角函数与解三角形
阶段提能(八) 解三角形
1.(人教A版必修第二册P47例8)在△ABC中,已知B=30°,b=,c=2,解这个三角形.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 由正弦定理,得
sin C===.
因为c>b,B=30°,所以30°于是C=45°,或C=135°.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(1)当C=45°时,A=105°.
此时a==
=
=
=
=+1.
(2)当C=135°时,A=15°.
此时a==
=
=
=
=-1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
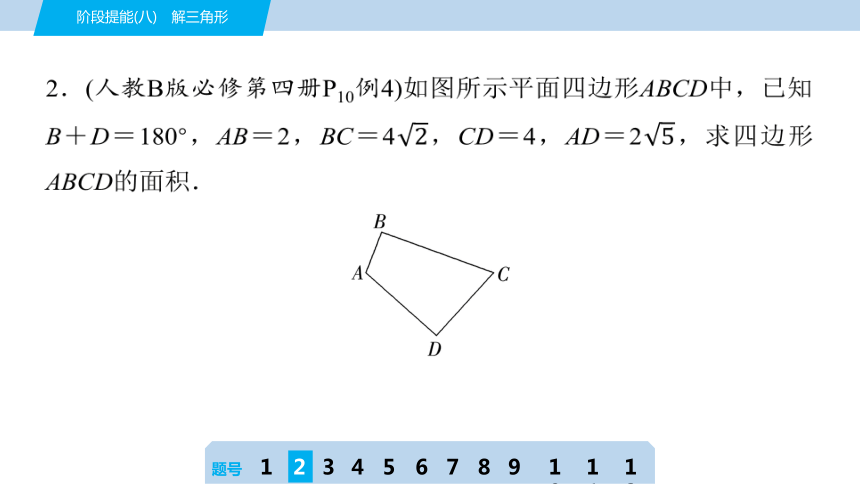
2.(人教B版必修第四册P10例4)如图所示平面四边形ABCD中,已知B+D=180°,AB=2,BC=4,CD=4,AD=2,求四边形ABCD的面积.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 连接AC,如图所示.
在△ABC与△ADC中分别使用余弦定理可得
AC2=AB2+BC2-2AB×BC cos B,
AC2=AD2+CD2-2AD×CD cos D.
又因为B+D=180°,所以cos D=cos (180°-B)=-cos B,
因此22+(4)2-2×2×4cos B=(2)2+42+2×2×4cos B.
解得cos B=0,因此cos D=0,则B=D=90°.
所以四边形ABCD的面积为×2×4×4×2=4().
题号
1
3
5
2
4
6
8
7
9
10
11
12
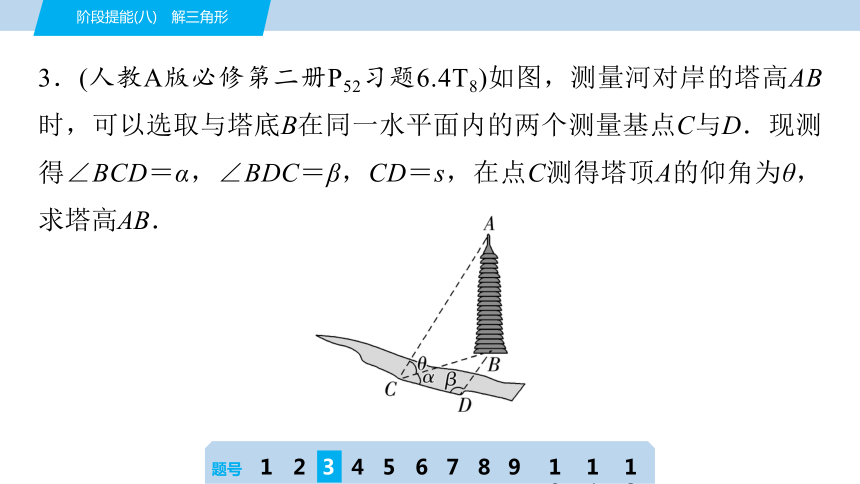
3.(人教A版必修第二册P52习题6.4T8)如图,测量河对岸的塔高AB时,可以选取与塔底B在同一水平面内的两个测量基点C与D.现测得∠BCD=α,∠BDC=β,CD=s,在点C测得塔顶A的仰角为θ,求塔高AB.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 由题意,∠BCD=α,∠BDC=β,CD=s,
∴∠CBD=π-α-β,
∴在△BCD中,由正弦定理得,
=,
∴==,
解得BC=,
∵在点C测得塔顶A的仰角为θ,
∴∠ACB=θ,
∴AB=BC tan θ=.
∴塔高AB为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
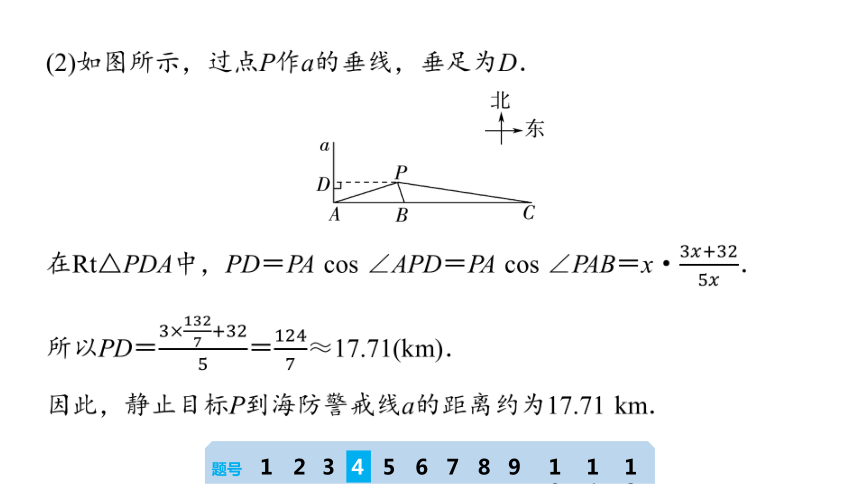
4.(北师大版必修第二册P124例12)如图所示,直线a表示海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在点A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,监测点A,C分别在8 s和20 s后相继收到这一信号.在当时的气象条件下,声波在水中传播速度的大小为1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
(2)求静止目标P到海防警戒线a的距离.(精确到0.01 km)
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)依题意,PA-PB=1.5×8=12(km),PC-PB=1.5×20=30(km).
因此PB=(x-12)km,PC=(18+x)km.
在△PAB中,AB=20 km,cos ∠PAB=
==.
同理cos ∠PAC=.
由cos ∠PAB=cos ∠PAC,得=.
解得x=.
(2)如图所示,过点P作a的垂线,垂足为D.
在Rt△PDA中,PD=PA cos ∠APD=PA cos ∠PAB=x·.
所以PD==≈17.71(km).
因此,静止目标P到海防警戒线a的距离约为17.71 km.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·全国甲卷)在△ABC中,内角A,B,C所对的边分别为a,b,c,若B=,b2=ac,则sin A+sin C=( )
A. B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为B=,b2=ac,则由正弦定理得sin Asin C=sin2B=.
由余弦定理可得:b2=a2+c2-2ac cosB=a2+c2-ac=ac,
即a2+c2=ac,根据正弦定理得sin2A+sin2C=sinA sin C=,
所以(sin A+sin C)2=sin2A+sin2C+2sinA sin C=,
因为A,C为三角形内角,则sin A>0,sin C>0,则sin A+sin C=.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2023·北京卷)在△ABC中,(a+c)(sin A-sin C)=b(sin A-
sin B),则∠C=( )
A. B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [由正弦定理得(a+c)(sin A-sin C)=b(sin A-sin B)可化为(a+c)(a-c)=b(a-b),
即a2+b2-c2=ab,
由余弦定理的推论可得,cos C===,
又C∈(0,π),所以C=.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2021·全国甲卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B,C三点,且A,B,C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100;由B点测得A点的仰角为45°,则A,C两点到水平面A′B′C′的高度差AA′-CC′约为(≈1.732)( )
A.346 B.373
C.446 D.473
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [如图所示,根据题意过C作CE∥C′B′,交BB′于E,过B作BD∥A′B′,交AA′于D,则BE=100,C′B′=CE=.
在△A′C′B′中,∠C′A′B′=75°,则BD=A′B′=.
又在B点处测得A点的仰角为45°,所以AD=BD=,所以高度差AA′-CC′=AD+BE=+100=+100=+100=+100=100(+1)+100≈373.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2024·春季上海卷)在△ABC中,BC=2,A=,B=,则AB=________.
[在△ABC中,A+B+C=π,C=,sin C=sin =sin cos +cos sin =,由正弦定理=,BC=2,A=,则AB===.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2022·全国甲卷)已知△ABC中,点D在边BC上,∠ADB=120°,AD=2,CD=2BD.当取得最小值时,BD=________.
-1 [设CD=2BD=2m>0,
则在△ABD中,AB2=BD2+AD2-2BD·AD cos ∠ADB=m2+4+2m,
在△ACD中,AC2=CD2+AD2-2CD·AD cos ∠ADC=4m2+4-4m,
-1
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以=
=
=4-
≥4-=4-2,当且仅当m+1=,即m=-1时,等号成立,所以当取最小值时,BD=m=-1.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2022·新高考Ⅱ卷)记△ABC的内角A,B,C的对边分别为a,b,c,分别以a,b,c为边长的三个正三角形的面积分别为S1,S2,S3,且S1-S2+S3=,sin B=.
(1)求△ABC的面积;
(2)若sin A sin C=,求b.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)∵边长为a的正三角形的面积为a2,
∴S1-S2+S3=(a2-b2+c2)=,即ac cos B=1,
由sin B=,得cos B=,∴ac==,
故S△ABC=ac sin B==.
(2)由正弦定理得:====,故b=sin B=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2023·新高考Ⅰ卷)已知在△ABC中,A+B=3C,2sin (A-C)=sin B.
(1)求sin A;
(2)设AB=5,求AB边上的高.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 法一:(1)在△ABC中,A+B=π-C,
因为A+B=3C,所以3C=π-C,所以C=.
因为2sin (A-C)=sin B,所以2sin =sin ,
展开并整理得(sin A-cos A)=(cos A+sin A),
得sin A=3cos A,又sin2A+cos2A=1,且sinA>0,
所以sin A=.
(2)由正弦定理=,
得BC=·sin A==3,
由余弦定理AB2=AC2+BC2-2AC·BC cos C,
得52=AC2+(3)2-2AC·3cos ,
整理得AC2-3AC+20=0,
解得AC=或AC=2.
题号
1
3
5
2
4
6
8
7
9
10
11
12
由(1)得,tan A=3>,所以<A<,
又A+B=,所以B>,
即C<B,所以AB<AC,所以AC=2.
设AB边上的高为h,则·AB·h=·AC·BC sin C,
即5h=2×3,
解得h=6,
所以AB边上的高为6.
题号
1
3
5
2
4
6
8
7
9
10
11
12
法二:(1)在△ABC中,A+B=π-C,
因为A+B=3C,所以3C=π-C,所以C=.
因为2sin (A-C)=sin B,
所以2sin (A-C)=sin [π-(A+C)]=sin (A+C),
所以2sin A cos C-2cos A sin C=sin A cos C+cos A sin C,
所以sin A cos C=3cos A sin C,
易得cos A cos C≠0,所以tan A=3tan C=3tan =3,
又sin A>0,所以sin A==.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)由(1)知sin A=,tan A=3>0,所以A为锐角,
所以cos A=,所以sin B=sin =(cos A+sin A)==,由正弦定理=,
得AC===2,
故AB边上的高为AC·sin A=2=6.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2023·新高考Ⅱ卷)记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC面积为,D为BC的中点,且AD=1.
(1)若∠ADC=,求tan B;
(2)若b2+c2=8,求b,c.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)因为D为BC的中点,
所以S△ABC=2S△ADC=2××AD×DC sin ∠ADC=2××1×DC×=,
解得DC=2,
所以BD=DC=2,a=4.
因为∠ADC=,所以∠ADB=.
在△ABD中,由余弦定理,得c2=AD2+BD2-2AD·BD cos ∠ADB=1+4+2=7,所以c=.
在△ADC中,由余弦定理,得b2=AD2+DC2-2AD·DC·cos ∠ADC=1+4-2=3,
所以b=.
在△ABC中,由余弦定理的推论,得cos B===,所以sin B==,
所以tanB==.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)因为D为BC的中点,所以BD=DC.
因为∠ADB+∠ADC=π,所以cos ∠ADB=-cos ∠ADC,
则在△ABD与△ADC中,由余弦定理,
得=-,即1+BD2-c2=-(1+BD2-b2),
所以2BD2=b2+c2-2=6,所以BD=,所以a=2.
在△ABC中,由余弦定理的推论,得cos ∠BAC===-,
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以S△ABC=bc sin ∠BAC
=bc
=bc
=
=,解得bc=4.
则由 解得b=c=2.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
第四章 三角函数与解三角形
阶段提能(八) 解三角形
1.(人教A版必修第二册P47例8)在△ABC中,已知B=30°,b=,c=2,解这个三角形.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 由正弦定理,得
sin C===.
因为c>b,B=30°,所以30°
题号
1
3
5
2
4
6
8
7
9
10
11
12
(1)当C=45°时,A=105°.
此时a==
=
=
=
=+1.
(2)当C=135°时,A=15°.
此时a==
=
=
=
=-1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教B版必修第四册P10例4)如图所示平面四边形ABCD中,已知B+D=180°,AB=2,BC=4,CD=4,AD=2,求四边形ABCD的面积.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 连接AC,如图所示.
在△ABC与△ADC中分别使用余弦定理可得
AC2=AB2+BC2-2AB×BC cos B,
AC2=AD2+CD2-2AD×CD cos D.
又因为B+D=180°,所以cos D=cos (180°-B)=-cos B,
因此22+(4)2-2×2×4cos B=(2)2+42+2×2×4cos B.
解得cos B=0,因此cos D=0,则B=D=90°.
所以四边形ABCD的面积为×2×4×4×2=4().
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教A版必修第二册P52习题6.4T8)如图,测量河对岸的塔高AB时,可以选取与塔底B在同一水平面内的两个测量基点C与D.现测得∠BCD=α,∠BDC=β,CD=s,在点C测得塔顶A的仰角为θ,求塔高AB.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 由题意,∠BCD=α,∠BDC=β,CD=s,
∴∠CBD=π-α-β,
∴在△BCD中,由正弦定理得,
=,
∴==,
解得BC=,
∵在点C测得塔顶A的仰角为θ,
∴∠ACB=θ,
∴AB=BC tan θ=.
∴塔高AB为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(北师大版必修第二册P124例12)如图所示,直线a表示海面上一条南北方向的海防警戒线,在a上点A处有一个水声监测点,另两个监测点B,C分别在点A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,监测点A,C分别在8 s和20 s后相继收到这一信号.在当时的气象条件下,声波在水中传播速度的大小为1.5 km/s.
(1)设PA=x km,用x分别表示PB,PC,并求x的值;
(2)求静止目标P到海防警戒线a的距离.(精确到0.01 km)
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)依题意,PA-PB=1.5×8=12(km),PC-PB=1.5×20=30(km).
因此PB=(x-12)km,PC=(18+x)km.
在△PAB中,AB=20 km,cos ∠PAB=
==.
同理cos ∠PAC=.
由cos ∠PAB=cos ∠PAC,得=.
解得x=.
(2)如图所示,过点P作a的垂线,垂足为D.
在Rt△PDA中,PD=PA cos ∠APD=PA cos ∠PAB=x·.
所以PD==≈17.71(km).
因此,静止目标P到海防警戒线a的距离约为17.71 km.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·全国甲卷)在△ABC中,内角A,B,C所对的边分别为a,b,c,若B=,b2=ac,则sin A+sin C=( )
A. B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为B=,b2=ac,则由正弦定理得sin Asin C=sin2B=.
由余弦定理可得:b2=a2+c2-2ac cosB=a2+c2-ac=ac,
即a2+c2=ac,根据正弦定理得sin2A+sin2C=sinA sin C=,
所以(sin A+sin C)2=sin2A+sin2C+2sinA sin C=,
因为A,C为三角形内角,则sin A>0,sin C>0,则sin A+sin C=.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2023·北京卷)在△ABC中,(a+c)(sin A-sin C)=b(sin A-
sin B),则∠C=( )
A. B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [由正弦定理得(a+c)(sin A-sin C)=b(sin A-sin B)可化为(a+c)(a-c)=b(a-b),
即a2+b2-c2=ab,
由余弦定理的推论可得,cos C===,
又C∈(0,π),所以C=.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2021·全国甲卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B,C三点,且A,B,C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100;由B点测得A点的仰角为45°,则A,C两点到水平面A′B′C′的高度差AA′-CC′约为(≈1.732)( )
A.346 B.373
C.446 D.473
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [如图所示,根据题意过C作CE∥C′B′,交BB′于E,过B作BD∥A′B′,交AA′于D,则BE=100,C′B′=CE=.
在△A′C′B′中,∠C′A′B′=75°,则BD=A′B′=.
又在B点处测得A点的仰角为45°,所以AD=BD=,所以高度差AA′-CC′=AD+BE=+100=+100=+100=+100=100(+1)+100≈373.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2024·春季上海卷)在△ABC中,BC=2,A=,B=,则AB=________.
[在△ABC中,A+B+C=π,C=,sin C=sin =sin cos +cos sin =,由正弦定理=,BC=2,A=,则AB===.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2022·全国甲卷)已知△ABC中,点D在边BC上,∠ADB=120°,AD=2,CD=2BD.当取得最小值时,BD=________.
-1 [设CD=2BD=2m>0,
则在△ABD中,AB2=BD2+AD2-2BD·AD cos ∠ADB=m2+4+2m,
在△ACD中,AC2=CD2+AD2-2CD·AD cos ∠ADC=4m2+4-4m,
-1
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以=
=
=4-
≥4-=4-2,当且仅当m+1=,即m=-1时,等号成立,所以当取最小值时,BD=m=-1.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2022·新高考Ⅱ卷)记△ABC的内角A,B,C的对边分别为a,b,c,分别以a,b,c为边长的三个正三角形的面积分别为S1,S2,S3,且S1-S2+S3=,sin B=.
(1)求△ABC的面积;
(2)若sin A sin C=,求b.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)∵边长为a的正三角形的面积为a2,
∴S1-S2+S3=(a2-b2+c2)=,即ac cos B=1,
由sin B=,得cos B=,∴ac==,
故S△ABC=ac sin B==.
(2)由正弦定理得:====,故b=sin B=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2023·新高考Ⅰ卷)已知在△ABC中,A+B=3C,2sin (A-C)=sin B.
(1)求sin A;
(2)设AB=5,求AB边上的高.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 法一:(1)在△ABC中,A+B=π-C,
因为A+B=3C,所以3C=π-C,所以C=.
因为2sin (A-C)=sin B,所以2sin =sin ,
展开并整理得(sin A-cos A)=(cos A+sin A),
得sin A=3cos A,又sin2A+cos2A=1,且sinA>0,
所以sin A=.
(2)由正弦定理=,
得BC=·sin A==3,
由余弦定理AB2=AC2+BC2-2AC·BC cos C,
得52=AC2+(3)2-2AC·3cos ,
整理得AC2-3AC+20=0,
解得AC=或AC=2.
题号
1
3
5
2
4
6
8
7
9
10
11
12
由(1)得,tan A=3>,所以<A<,
又A+B=,所以B>,
即C<B,所以AB<AC,所以AC=2.
设AB边上的高为h,则·AB·h=·AC·BC sin C,
即5h=2×3,
解得h=6,
所以AB边上的高为6.
题号
1
3
5
2
4
6
8
7
9
10
11
12
法二:(1)在△ABC中,A+B=π-C,
因为A+B=3C,所以3C=π-C,所以C=.
因为2sin (A-C)=sin B,
所以2sin (A-C)=sin [π-(A+C)]=sin (A+C),
所以2sin A cos C-2cos A sin C=sin A cos C+cos A sin C,
所以sin A cos C=3cos A sin C,
易得cos A cos C≠0,所以tan A=3tan C=3tan =3,
又sin A>0,所以sin A==.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)由(1)知sin A=,tan A=3>0,所以A为锐角,
所以cos A=,所以sin B=sin =(cos A+sin A)==,由正弦定理=,
得AC===2,
故AB边上的高为AC·sin A=2=6.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2023·新高考Ⅱ卷)记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC面积为,D为BC的中点,且AD=1.
(1)若∠ADC=,求tan B;
(2)若b2+c2=8,求b,c.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)因为D为BC的中点,
所以S△ABC=2S△ADC=2××AD×DC sin ∠ADC=2××1×DC×=,
解得DC=2,
所以BD=DC=2,a=4.
因为∠ADC=,所以∠ADB=.
在△ABD中,由余弦定理,得c2=AD2+BD2-2AD·BD cos ∠ADB=1+4+2=7,所以c=.
在△ADC中,由余弦定理,得b2=AD2+DC2-2AD·DC·cos ∠ADC=1+4-2=3,
所以b=.
在△ABC中,由余弦定理的推论,得cos B===,所以sin B==,
所以tanB==.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)因为D为BC的中点,所以BD=DC.
因为∠ADB+∠ADC=π,所以cos ∠ADB=-cos ∠ADC,
则在△ABD与△ADC中,由余弦定理,
得=-,即1+BD2-c2=-(1+BD2-b2),
所以2BD2=b2+c2-2=6,所以BD=,所以a=2.
在△ABC中,由余弦定理的推论,得cos ∠BAC===-,
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以S△ABC=bc sin ∠BAC
=bc
=bc
=
=,解得bc=4.
则由 解得b=c=2.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
同课章节目录
