《高考快车道》2026版高三一轮总复习数学(基础版)57 第六章 第1课时 数列的概念与简单表示法 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)57 第六章 第1课时 数列的概念与简单表示法 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:56 | ||
图片预览










文档简介
(共89张PPT)
第六章 数列
第六章 数列
第六章 数列
必修1 中国特色社会主义
第六章 数列
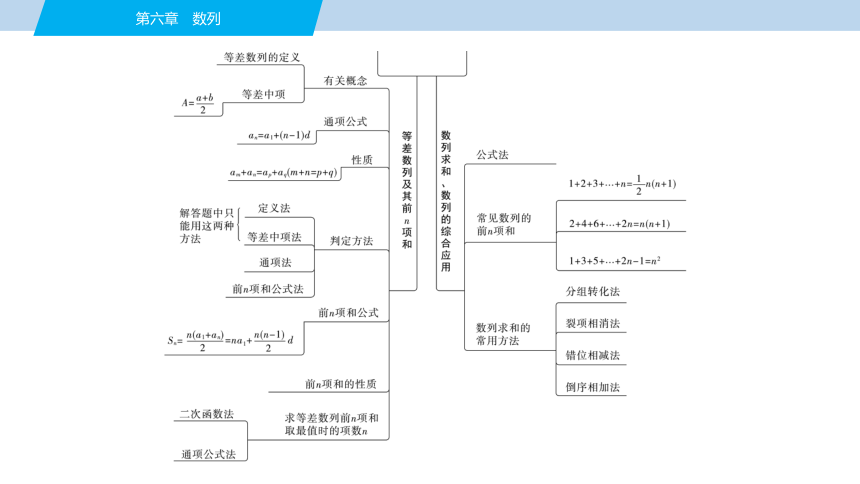
等比数列是高考的重点和热点,一是考查利用等比数列的通项公式、前n项和公式进行基本量运算,多以选择题、填空题形式呈现,属于中低难度题;二是考查等比数列的证明、等比数列的性质、通项公式及前n项和等,多以解答题形式呈现,难度中等.
必修1 中国特色社会主义
第六章 数列
(12分)(2024·全国甲卷T18)记Sn为数列{an}的前n项和,已知4Sn=3an+4.
(1)求{an}的通项公式;
(2)设bn=(-1)n-1nan,求数列{bn}的前n项和Tn.
[阅读与思考] (1)第1步:根据数列中an和Sn的关系求数列{an}的递推关系.
因为4Sn=3an+4,①
所以当n≥2时,4Sn-1=3an-1+4,②……………………………(1分)
则当n≥2时,①-②得4an=3an-3an-1,
即an=-3an-1.……………………………………………………(3分)
第2步:求出a1.
当n=1时,由4Sn=3an+4,得4a1=3a1+4,所以a1=4≠0,
………………………………………………………………………(4分)
第3步:求数列{an}的通项公式.
所以数列{an}是以4为首项,-3为公比的等比数列,
所以an=4×(-3)n-1.………………………………………………(5分)
(2)第1步:求出数列{bn}的通项公式.
因为bn=(-1)n-1nan=(-1)n-1n×4×(-3)n-1=4n·3n-1,…………(7分)
第2步:利用错位相减法求Tn.
所以Tn=4×30+8×31+12×32+…+4n·3n-1,
3Tn=4×31+8×32+12×33+…+4n·3n,………………………(8分)
两式相减得-2Tn=4+4(31+32+…+3n-1)-4n·3n
=4+4×-4n·3n
=-2+(2-4n)·3n,……………………………………………(11分)
所以Tn=1+(2n-1)·3n.………………………………………(12分)
必修1 中国特色社会主义
第六章 数列
归纳总结:若一个数列的通项公式为anbn的形式,其中数列{an}为等差数列,数列{bn}为等比数列,则求数列{anbn}的前n项和时,可以利用错位相减法.
必修1 中国特色社会主义
第六章 数列
本题第(1)问源自人教A版教材选择性必修第二册P56复习参考题4T12(1).这一问教材习题和高考题在解法上完全相同,难度相当,都是考查由数列的递推关系式求数列的通项公式.本题第(2)问源自人教A版教材选择性必修第二册P56复习参考题4T11(2).教材习题第(1)问求得an=2n-1后,则第(2)问cn=(2n-1)·3n-1与高考题第(2)问bn=4n·3n-1的通项公式都是等差数列与等比数列“积”的形式,用“错位相减法”求和.高考题难度稍高于教材习题,在于多了一步幂运算,即bn=
(-1)n-1nan=(-1)n-1n×4×(-3)n-1=(-1)n-1n×4×(-1)n-1×3n-1=
(-1)2(n-1)n×4×3n-1=4n×3n-1.
必修1 中国特色社会主义
第六章 数列
试题评价:本题以数列的前n项和与通项之间的关系为载体,考查数列问题中已知数列的递推关系的条件下,求数列的通项公式及错位相减法求和,属于课程学习情境,难度中等,体现了数学运算、逻辑推理的数学核心素养.
附:1.(人教A版选择性必修第二册复习参考题4P56T12(1))已知等比数列{an}的前n项和为Sn,且an+1=2Sn+2(n∈N*).(1)求数列{an}的通项公式.
2.(人教A版选择性必修第二册复习参考题4P56T11(2))已知等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1(n∈N*).(2)若bn=3n-1,令cn=anbn,求数列{cn}的前n项和Tn.
第1课时 数列的概念与简单表示法
[考试要求] 1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式).
2.了解数列是自变量为正整数的一类特殊函数.
考点一 由an与Sn的关系求通项公式
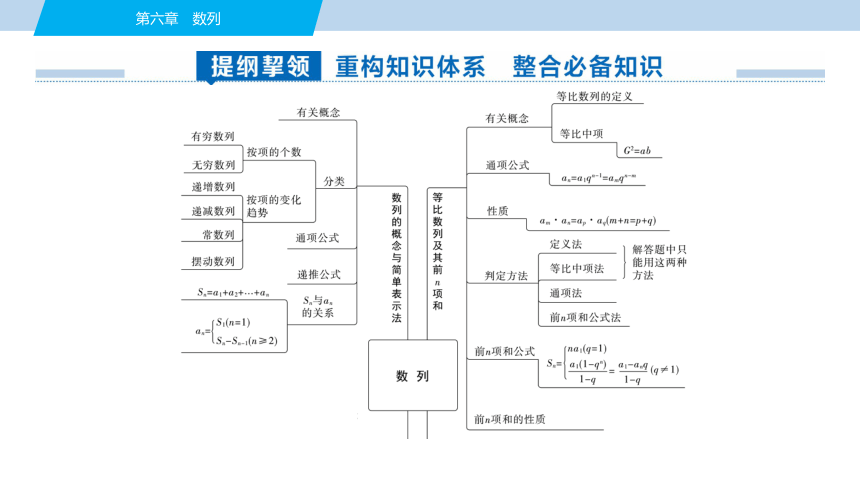
1.数列的定义
一般地,把按照__________排列的一列数称为数列,数列中的每一个数叫做这个数列的项.
2.数列的前n项和
(1)表示:在数列{an}中,Sn=__________________叫做数列的前n项和.
(2)an与Sn的关系:若数列{an}的前n项和为Sn,
则an=
提醒:若a1满足an=Sn-Sn-1(n≥2),则不需要分段.
确定的顺序
a1+a2+…+an
S1
Sn-Sn-1
[典例1] (1)(人教A版选择性必修第二册P8练习T4改编)数列{an}的前n项和Sn=2n2+n+1,那么{an}的通项公式是
(2)(2024·全国甲卷节选)已知等比数列{an}的前n项和为Sn,且2Sn=3an+1-3.求{an}的通项公式.
an=
__________________.
(1)an= [当n=1时,a1=S1=2×12+1+1=4,
当n≥2时,an=Sn-Sn-1=2n2+n+1-[2(n-1)2+(n-1)+1]=4n-1.
由于a1=4不满足上式,
所以an=]
(2)[解] 因为2Sn=3an+1-3,故2Sn-1=3an-3,
所以2an=3an+1-3an(n≥2),即5an=3an+1,故等比数列的公比q=,
故2a1=3a2-3=3a1×-3=5a1-3,故a1=1,故an=.
【教用·备选题】
母题探究 本例(1)中,若Sn=2n2+n,求an.
[解] 当n=1时,a1=3,
当n≥2时,an=Sn-Sn-1=2n2+n-[2(n-1)2+(n-1)]=4n-1,
由于a1=3满足上式,
所以an=4n-1(n∈N*).
反思领悟 本例(1)由Sn=2n2+n+1求an时,先分n=1,n≥2两种情况讨论,然后验证能否合并为同一个表达式;本例(2)利用an=Sn-Sn-1(n≥2)转化为只含an,an+1的关系式5an=3an+1,再求解.
巩固迁移1 (1)(2024·抚州临川二中月考)已知数列{an},Sn是其前n项和,且Sn=2an+1,则数列{an}的通项公式an=________.
(2)(2024·榆林模拟)已知数列{an}满足a1+2a2+3a3+…+nan=2n,则an=
-2n-1
_____________.
(1)-2n-1 (2) [(1)当n=1时,a1=S1=2a1+1,∴a1=-1.
当n≥2时,Sn=2an+1,①
Sn-1=2an-1+1.②
①-②,得Sn-Sn-1=2an-2an-1,
即an=2an-2an-1,即an=2an-1(n≥2),
∴数列{an}是首项a1=-1,公比q=2的等比数列,
∴an=a1·qn-1=-2n-1.
(2)当n=1时,a1=21=2,
∵a1+2a2+3a3+…+nan=2n,①
故当n≥2时,a1+2a2+3a3+…+(n-1)an-1=2n-1,②
由①-②,得nan=2n-2n-1=2n-1,
∴an=(n≥2).
显然a1=2不满足上式,
∴an=]
考点二 由数列的递推关系求通项公式
1.数列有三种表示法,它们分别是______、______和________.
2.通项公式:如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
3.递推公式:如果一个数列的相邻两项或多项之间的关系可以用________来表示,那么这个式子叫做这个数列的递推公式.
列表法
图象法
解析式法
一个式子
[典例2] (1)(2024·南阳月考)已知数列{an}满足an+1=an,a1=1,则a11=( )
A. B.
C. D.
√
(2)(2025·济南历下区模拟)围棋起源于中国,至今已有4 000多年的历史.在围棋中,对于一些复杂的死活问题,比如在判断自己单个眼内的气数是否满足需求时,可利用数列通项的递推方法来计算.假设大小为n的眼有an口气,大小为n+1的眼有an+1口气,则an与an+1满足的关系是a1=1,a2=2,an+1-n=an-1(n≥2,n∈N*),则{an}的通项公式为
_________________.
an=
(1)B (2)an= [(1)a11=a10=a9=a8=…=×…×a1=a1=.故选B.
(2)已知an+1-n=an-1(n≥2,n∈N*),
则an+1-an=n-1,
即n≥3时,an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2
=(n-2)+(n-3)+…+1+2=+2=,
又因为当n=2时,a2=2满足上式,
当n=1时,a1=1不满足上式,
所以an=]
反思领悟 本例(1),an+1=an这一递推关系可化为=的形式,可用累乘法:×…×=×…×,即a11=×a1=, 也可用本例解答中的方法;
本例(2),an+1-an=n-1这一递推关系,一般用累加法求和,但一定要注意能消去多少项,保留多少项.
巩固迁移2 (1)在数列{an}中,a1=2,an+1=an+,则an=________.
(2)若数列{an}满足a1=1,nan-1=(n+1)an(n≥2),则an=_______.
(1)3- (2) [(1)因为当n≥2时,an-an-1==,
所以当n≥2时,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=+…++2=3-.
当n=1时,满足上式.故an=3-.
3-
(2)由nan-1=(n+1)an(n≥2),
得=(n≥2).
所以an=·…··a1=×…××1=,
又因为a1=1也满足上式,所以an=.]
考点三 数列的函数特性
分类标准 类型 满足条件
按项数 分类 有穷数列 项数____
无穷数列 项数____
按项与项间的大小关系分类 递增数列 an+1__an 其中
n∈N*
递减数列 an+1__an
常数列 an+1=an
有限
无限
>
<
分类标准 类型 满足条件
按其他 标准分类 摆动数列 从第2项起,有些项大于它的前一项,有些项小于它的前一项
周期数列 对n∈N*,存在正整数k,使an+k=an
[常用结论] 在数列{an}中,若an最大,则(n≥2),若an最小,则(n≥2).
考向1 数列的周期性
[典例3] (2024·海宁市月考)已知数列{an},a1=4,a2=1,an+2=an+1-an(n∈N*),则a2 025=( )
A.4 B.3
C.-3 D.-4
√
C [因为a1=4,a2=1,an+2=an+1-an(n∈N*),
所以a3=a2-a1=1-4=-3,
a4=a3-a2=-3-1=-4,
a5=a4-a3=-4-(-3)=-1,
a6=a5-a4=-1-(-4)=3,
a7=a6-a5=3-(-1)=4,
a8=a7-a6=4-3=1,
……
所以数列{an}是以6为周期的数列,
所以a2 025=a337×6+3=a3=-3.故选C.]
反思领悟 本例由递推关系a1=4,a2=1,an+2=an+1-an计算出a3,a4,a5,a6,a7,a8,观察并发现数列{an}中,a1,a2,…a6,a7,a8…每6项循环出现一次,故数列{an}的周期为6,进而可求
a2 025.由递推公式计算出一些项,观察并发现周期,是数列求周期的最实用方法.
巩固迁移3 (2024·哈尔滨南岗区月考)若数列{an}满足an+1=,a3=3,则a2 025=( )
A.- B.
C. D.3
√
D [因为an+1=,a3=3,
所以a3==3,解得a2=.
又a2==,解得a1=-.
又a4==-,a5==,a6==3,
显然,接下去a7=-,a8=,a9=3,…,
所以数列{an}是以3为周期的数列,则a2 025=a674×3+3=a3=3.故选D.]
考向2 数列的单调性
[典例4] 已知数列{an}的通项公式为an=,若数列{an}为递减数列,则实数k的取值范围为( )
A.(3,+∞) B.(2,+∞)
C.(1,+∞) D.(0,+∞)
√
D [因为an+1-an==,
由数列{an}为递减数列知,
对于任意的n∈N*,an+1-an=<0,所以k>3-3n对于任意的n∈N*恒成立,所以k∈(0,+∞).故选D.]
反思领悟 数列是特殊的函数,利用数列的单调性求参数实质是函数中的恒成立问题.如本例中,由{an}递减可得an+1-an<0,即k>3-3n恒成立.
巩固迁移4 (2024·秦皇岛月考)已知数列{an}是递增数列,则其通项公式可以是( )
A.an=n2-n B.an=3n-9n
C.an= D.an=3n-1-2n
√
A [对于A,an=n2-n,
则an+1-an=(n+1)2-(n+1)-n2+n=2n>0,是递增数列,A正确;
对于B,an=3n-9n,
则a1=-6,a2=-9,不是递增数列,故B错误;
对于C,an=
则a5=25,a6=13,不是递增数列,故C错误;
对于D,an=3n-1-2n,
则a1=a2=-1,不是递增数列,故D错误.故选A.]
考向3 数列的最值
[典例5] (2024·沈阳期末)已知数列{an}的通项公式为an=,则此数列的最大项为( )
A. B.
C. D.
√
D [法一:an+1-an==,
当n<8时,an+1-an>0,即an+1>an;
当n=8时,an+1-an=0,即an+1=an;
当n>8时,an+1-an<0,即an+1<an,
所以a1<a2<a3<…<a8=a9>a10>a11>…,
所以数列{an}有最大项,为第8项和第9项,且a8=a9==.
法二:设数列{an}的第n项最大,则(n≥2),
即
解得8≤n≤9,又n∈N*,则n=8或n=9,
故数列{an}有最大项,为第8项和第9项,且a8=a9=.
故选D.]
反思领悟 本例法一,求出an+1-an=后,利用函数单调性求{an}的最大项,法二利用(n≥2)确定最大项.
巩固迁移5 (2025·锦州模拟)数列{an}的通项公式为an=,该数列的前50项中最大项是( )
A.a1 B.a44
C.a45 D.a50
√
C [an==
=1+,
因为>0,∈(44,45),
当n≤44时,数列{an}递减,且an<1,
当n≥45时,数列{an}递减,且an>1,
当n=45时,取得最大项.
故选C.]
随堂练习
√
1.(2024·石景山期末)在数列{an}中,a1=-2,an+1=1-(n∈N*),则a2 025的值为( )
A.-2 B.
C. D.
B [由a1=-2,an+1=1-(n∈N*),可得a2=1-=,
a3=1-=,a4=1-3=-2=a1,
a5=1-==a2,…,
即数列{an}是周期为3的数列,
则a2 025=a3×674+3=a3=.
故选B.]
2.(2024·琼海期末)下列四个选项中,不正确的是( )
A.数列的图象是一群孤立的点
B.数列1,0,1,0,…与数列0,1,0,1,…是同一数列
C.数列,…的一个通项公式是an=(n∈N*)
D.数列,…,是递减数列
√
B [根据数列的函数特性可知,数列的图象是一群孤立的点,A正确;
根据数列的定义可知,数列的项具有一定的顺序,B错误;
数列…的一个通项公式是an=,C正确;
根据数列单调性的定义可知,D正确.
故选B.]
3.(2024·唐山二模)已知数列{an}满足an+1=an+a1+2n,a10=130,则a1=( )
A.1 B.2
C.3 D.4
√
D [由an+1=an+a1+2n,可得an+1-an=a1+2n,
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=a1+(a1+2)+(a1+4)+…+(a1+2n-2)
=na1+(n-1)(2+2n-2)=na1+n(n-1),
由a10=130,可得10a1+90=130,解得a1=4.故选D.]
4.(2024·鄂尔多斯期末)已知数列{an}的前n项和Sn=2n,则a3+a4=________.
12 [由数列{an}的前n项和Sn=2n,
可得a3+a4=S4-S2=24-22=12.]
12
【教用·备选题】
1.已知数列{an}满足a1=3,an+1+an=2,则a22=( )
A.3 B.2
C.1 D.-1
√
D [因为数列{an}满足a1=3,an+1+an=2,
所以a1=3,a2=-1,a3=3,a4=-1,…,
故数列{an}是周期为2的数列,所以a22=a2=-1.
故选D.]
2.(2024·南昌月考)已知数列{an}是递增数列,且an=则a的取值范围是( )
A. B.
C. D.
√
D [根据题意,因为数列{an}是递增数列,且an=
所以
解得则a的取值范围是.故选D.]
3.(2024·茂名一模)数列{an}满足a1=8,an+1=(n∈N*),bn=,若数列{bn}是递减数列,则实数λ的取值范围是
( )
A. B.
C. D.
√
D [由题意an+1=,两边取倒数可化为==+n,即=n,
所以=1,=2,…,=n-1,
由累加法可得=1+2+…+(n-1)=,
因为a1=8,所以==,
所以bn==,
因为数列{bn}是递减数列,故bn<bn-1(n≥2),
所以<,
即λ>=-+1,
因为n≥2且n∈N*,故当n=2或n=3时,+1取得最大值,故λ>.故选D.]
4.(2025·房山区模拟)设Sn为数列{an}的前n项和,且Sn=n2-n,则a5=________;数列{an}的通项公式an=________.
8 2n-2 [由Sn为数列{an}的前n项和,且Sn=n2-n,得
当n=1时,a1=S1=0,
当n≥2时,an=Sn-Sn-1=n2-n-(n-1)2+(n-1)=2n-2,
当n=1时,上式成立,所以an=2n-2,a5=8.]
8
2n-2
5.(2025·湘西州模拟)已知数列{an}的前n项和Sn满足Sn=2an+2,则S5=________.
-62 [令n=1,得a1=S1=2a1+2,所以a1=-2,
Sn=2an+2,当n≥2时,Sn-1=2an-1+2,两式相减得,
Sn-Sn-1=2an-2an-1,即an=2an-2an-1,即=2,
所以数列{an}是首项为-2,公比为2的等比数列,
所以S5==-62.]
-62
6.(2025·湖北武汉模拟)九连环是我国从古至今广泛流传的一种益智游戏,它用九个圆环相连成串,以解开为胜.用an表示解下n(n≤9,n∈N*)个圆环所需的最少移动次数.若a1=1,且an+1=
则解下6个圆环所需的最少移动次数为________.
64 [因为a1=1,所以a2=2a1+2=4,a3=2a2-1=7,a4=2a3+2=16,a5=2a4-1=31,a6=2a5+2=64.]
64
课后习题(三十七) 数列的概念与简单表示法
1.(人教A版选择性必修第二册P8练习T4改编)已知数列{an}的前n项和为Sn,且Sn=3n2+2n,则数列{an}的通项公式为an=________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
6n-1
题号
1
3
5
2
4
6
8
7
9
10
11
12
6n-1 [由题知,Sn=3n2+2n,则Sn-1=3(n-1)2+2(n-1)=3n2-4n+1(n≥2),an=Sn-Sn-1=6n-1(n≥2),又a1=S1=5,符合上式,所以an=6n-1(n∈N*).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版选择性必修第二册P9习题4.1T7改编)设数列{an}的通项公式为an=n2+kn,若数列{an}是递增数列,则实数k的取值范围为___________.
(-3,+∞) [由数列{an}是递增数列,可得an+1>an对于任意的n∈N*恒成立,即(n+1)2+k(n+1)>n2+kn,即2n+1+k>0,即k>
-2n-1对于任意的n∈N*恒成立.因为f (n)=-2n-1(n∈N*)递减,所以f (n)max=f (1)=-3,所以k>-3.]
(-3,+∞)
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(苏教版选择性必修第一册P139习题4.1T8改编)已知数列{an}的通项公式为an=(n∈N*),则数列{an}的最大项为第________项.
4 [法一:因为an+1-an==,
所以当n≥4时,an+1an,
即a1a5>a6>…,
故数列{an}的最大项为第4项.
4
题号
1
3
5
2
4
6
8
7
9
10
11
12
法二:设数列{an}中的最大项为ak,则(k≥2),
即解得≤k≤.
因为k∈N*,所以k=4.
故数列{an}的最大项为第4项.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第二册P9习题4.1T4改编)已知数列{an}的前n项和为Sn,a1=,Sn=n2·an,bn=.
(1)写出数列{bn}的前4项;
(2)求出数列{an}的通项公式.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)因为Sn=n2·an,①
所以Sn+1=(n+1)2·an+1,②
②-①,得an+1=(n+1)2·an+1-n2·an,
所以=,所以bn=,
所以b1=,b2=,b3=,b4=.
(2)当n≥2时,由=,得===,…,=,所以·…·=×…×,
即=(n≥2),
又因为a1=,所以an=(n≥2).
当n=1时,a1=满足上式,故an=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2025·开封模拟)已知数列{an}的前n项和为Sn=3n-1,则a5=
( )
A.81 B.162
C.243 D.486
√
B [因为Sn=3n-1,所以a5=S5-S4=35-1-34+1=162.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·辽宁月考)在数列{an}中,若a1=,an+1=2-,则下列数不是{an}中的项的是( )
A.-2 B.-1
C. D.3
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [因为a1=,an+1=2-,
所以a2=2-=,a3=2-=-2,a4=2-=3,
a5=2-=,
所以数列{an}是以4为周期的数列,故-1不是{an}中的项.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·中山市月考)已知n∈N*,下列数列是递增数列的是( )
A.an= B.an=1-2n
C.an=n2 D.an=
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [对于A,an-an-1==-<0,故{an}为递减数列,故A错误;
对于B,an-an-1=-2<0,故{an}为递减数列,故B错误;
对于C,an-an-1=2n-1>0,故{an}为递增数列,故C正确;
对于D,an-an-1==-<0,故{an}为递减数列,故D错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2025·江苏常州模拟)已知数列{an}的前5项依次为2,0,2,0,2,则下列可以作为数列{an}的通项公式的有( )
A.an= B.an=(-1)n+1
C.an=2 D.an=4
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AC [数列{an}的前5项依次为2,0,2,0,2,
经验证,AC选项,显然可以表示,
对于B,当n=1时,a1=0,故B错误;
对于D,当n=2时,a2=2,故D错误.故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·韩城市期末)设数列{an}满足a1++…+=1-,则an=( )
A.1- B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [∵a1++…+=1-,①
∴当n=1时,a1=1-=.
当n≥2时,a1++…+=1-,②
∴①-②,得=1-=,
∴an=.
当n=1时也成立,∴an=.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·遵义月考)下表中的数阵为“森德拉姆筛”,其特点是每行每列都成等差数列.
2 3 4 5 6 7 …
3 5 7 9 11 13 …
4 7 10 13 16 19 …
5 9 13 17 21 25 …
6 11 16 21 26 31 …
7 13 19 25 31 37 …
… … … … … … …
表中对角线上的一列数2,5,10,17,26,37,…构成数列{an},则a985=( )
A.9852-1 B.9852+1
C.9862-1 D.9862+1
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [根据题意,数列{an}的前几项为2,5,10,17,26,37,…,
归纳可得其递推公式为an+1-an=2n+1,a1=2,
所以an-an-1=2n-1,an-1-an-2=2n-3,…,a2-a1=3,
累加得an-a1=3+5+7+…+(2n-1),
所以an-2==n2-1,所以an=n2+1,
故a985=9852+1.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·江苏启东中学月考)若数列{an}的前n项和Sn=n2-10n(n∈N*),则数列{an}的通项公式an=________,数列{nan}中数值最小的项是第________项.
2n-11
3
题号
1
3
5
2
4
6
8
7
9
10
11
12
2n-11 3 [∵Sn=n2-10n,
∴当n≥2时,an=Sn-Sn-1=2n-11,
当n=1时,a1=S1=-9也适合上式.
∴an=2n-11(n∈N*).
令f (n)=nan=n(2n-11)=2n2-11n,
此函数图象的对称轴为直线n=,但n∈N*,
∴当n=3时,f (n)取得最小值.
∴数列{nan}中数值最小的项是第3项.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·四川绵阳调研)已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则数列{an}的通项公式为
an=
______________________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
an= [因为Sn=2an+1,①
a1=1,当n=1时,S1=a1=2a2,所以a2=.
当n≥2时,Sn-1=2an,②
①-②,得an=2an+1-2an,即=(n≥2).
所以当n≥2时,an=a2·=,
故an=]
谢 谢 !
第六章 数列
第六章 数列
第六章 数列
必修1 中国特色社会主义
第六章 数列
等比数列是高考的重点和热点,一是考查利用等比数列的通项公式、前n项和公式进行基本量运算,多以选择题、填空题形式呈现,属于中低难度题;二是考查等比数列的证明、等比数列的性质、通项公式及前n项和等,多以解答题形式呈现,难度中等.
必修1 中国特色社会主义
第六章 数列
(12分)(2024·全国甲卷T18)记Sn为数列{an}的前n项和,已知4Sn=3an+4.
(1)求{an}的通项公式;
(2)设bn=(-1)n-1nan,求数列{bn}的前n项和Tn.
[阅读与思考] (1)第1步:根据数列中an和Sn的关系求数列{an}的递推关系.
因为4Sn=3an+4,①
所以当n≥2时,4Sn-1=3an-1+4,②……………………………(1分)
则当n≥2时,①-②得4an=3an-3an-1,
即an=-3an-1.……………………………………………………(3分)
第2步:求出a1.
当n=1时,由4Sn=3an+4,得4a1=3a1+4,所以a1=4≠0,
………………………………………………………………………(4分)
第3步:求数列{an}的通项公式.
所以数列{an}是以4为首项,-3为公比的等比数列,
所以an=4×(-3)n-1.………………………………………………(5分)
(2)第1步:求出数列{bn}的通项公式.
因为bn=(-1)n-1nan=(-1)n-1n×4×(-3)n-1=4n·3n-1,…………(7分)
第2步:利用错位相减法求Tn.
所以Tn=4×30+8×31+12×32+…+4n·3n-1,
3Tn=4×31+8×32+12×33+…+4n·3n,………………………(8分)
两式相减得-2Tn=4+4(31+32+…+3n-1)-4n·3n
=4+4×-4n·3n
=-2+(2-4n)·3n,……………………………………………(11分)
所以Tn=1+(2n-1)·3n.………………………………………(12分)
必修1 中国特色社会主义
第六章 数列
归纳总结:若一个数列的通项公式为anbn的形式,其中数列{an}为等差数列,数列{bn}为等比数列,则求数列{anbn}的前n项和时,可以利用错位相减法.
必修1 中国特色社会主义
第六章 数列
本题第(1)问源自人教A版教材选择性必修第二册P56复习参考题4T12(1).这一问教材习题和高考题在解法上完全相同,难度相当,都是考查由数列的递推关系式求数列的通项公式.本题第(2)问源自人教A版教材选择性必修第二册P56复习参考题4T11(2).教材习题第(1)问求得an=2n-1后,则第(2)问cn=(2n-1)·3n-1与高考题第(2)问bn=4n·3n-1的通项公式都是等差数列与等比数列“积”的形式,用“错位相减法”求和.高考题难度稍高于教材习题,在于多了一步幂运算,即bn=
(-1)n-1nan=(-1)n-1n×4×(-3)n-1=(-1)n-1n×4×(-1)n-1×3n-1=
(-1)2(n-1)n×4×3n-1=4n×3n-1.
必修1 中国特色社会主义
第六章 数列
试题评价:本题以数列的前n项和与通项之间的关系为载体,考查数列问题中已知数列的递推关系的条件下,求数列的通项公式及错位相减法求和,属于课程学习情境,难度中等,体现了数学运算、逻辑推理的数学核心素养.
附:1.(人教A版选择性必修第二册复习参考题4P56T12(1))已知等比数列{an}的前n项和为Sn,且an+1=2Sn+2(n∈N*).(1)求数列{an}的通项公式.
2.(人教A版选择性必修第二册复习参考题4P56T11(2))已知等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1(n∈N*).(2)若bn=3n-1,令cn=anbn,求数列{cn}的前n项和Tn.
第1课时 数列的概念与简单表示法
[考试要求] 1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式).
2.了解数列是自变量为正整数的一类特殊函数.
考点一 由an与Sn的关系求通项公式
1.数列的定义
一般地,把按照__________排列的一列数称为数列,数列中的每一个数叫做这个数列的项.
2.数列的前n项和
(1)表示:在数列{an}中,Sn=__________________叫做数列的前n项和.
(2)an与Sn的关系:若数列{an}的前n项和为Sn,
则an=
提醒:若a1满足an=Sn-Sn-1(n≥2),则不需要分段.
确定的顺序
a1+a2+…+an
S1
Sn-Sn-1
[典例1] (1)(人教A版选择性必修第二册P8练习T4改编)数列{an}的前n项和Sn=2n2+n+1,那么{an}的通项公式是
(2)(2024·全国甲卷节选)已知等比数列{an}的前n项和为Sn,且2Sn=3an+1-3.求{an}的通项公式.
an=
__________________.
(1)an= [当n=1时,a1=S1=2×12+1+1=4,
当n≥2时,an=Sn-Sn-1=2n2+n+1-[2(n-1)2+(n-1)+1]=4n-1.
由于a1=4不满足上式,
所以an=]
(2)[解] 因为2Sn=3an+1-3,故2Sn-1=3an-3,
所以2an=3an+1-3an(n≥2),即5an=3an+1,故等比数列的公比q=,
故2a1=3a2-3=3a1×-3=5a1-3,故a1=1,故an=.
【教用·备选题】
母题探究 本例(1)中,若Sn=2n2+n,求an.
[解] 当n=1时,a1=3,
当n≥2时,an=Sn-Sn-1=2n2+n-[2(n-1)2+(n-1)]=4n-1,
由于a1=3满足上式,
所以an=4n-1(n∈N*).
反思领悟 本例(1)由Sn=2n2+n+1求an时,先分n=1,n≥2两种情况讨论,然后验证能否合并为同一个表达式;本例(2)利用an=Sn-Sn-1(n≥2)转化为只含an,an+1的关系式5an=3an+1,再求解.
巩固迁移1 (1)(2024·抚州临川二中月考)已知数列{an},Sn是其前n项和,且Sn=2an+1,则数列{an}的通项公式an=________.
(2)(2024·榆林模拟)已知数列{an}满足a1+2a2+3a3+…+nan=2n,则an=
-2n-1
_____________.
(1)-2n-1 (2) [(1)当n=1时,a1=S1=2a1+1,∴a1=-1.
当n≥2时,Sn=2an+1,①
Sn-1=2an-1+1.②
①-②,得Sn-Sn-1=2an-2an-1,
即an=2an-2an-1,即an=2an-1(n≥2),
∴数列{an}是首项a1=-1,公比q=2的等比数列,
∴an=a1·qn-1=-2n-1.
(2)当n=1时,a1=21=2,
∵a1+2a2+3a3+…+nan=2n,①
故当n≥2时,a1+2a2+3a3+…+(n-1)an-1=2n-1,②
由①-②,得nan=2n-2n-1=2n-1,
∴an=(n≥2).
显然a1=2不满足上式,
∴an=]
考点二 由数列的递推关系求通项公式
1.数列有三种表示法,它们分别是______、______和________.
2.通项公式:如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
3.递推公式:如果一个数列的相邻两项或多项之间的关系可以用________来表示,那么这个式子叫做这个数列的递推公式.
列表法
图象法
解析式法
一个式子
[典例2] (1)(2024·南阳月考)已知数列{an}满足an+1=an,a1=1,则a11=( )
A. B.
C. D.
√
(2)(2025·济南历下区模拟)围棋起源于中国,至今已有4 000多年的历史.在围棋中,对于一些复杂的死活问题,比如在判断自己单个眼内的气数是否满足需求时,可利用数列通项的递推方法来计算.假设大小为n的眼有an口气,大小为n+1的眼有an+1口气,则an与an+1满足的关系是a1=1,a2=2,an+1-n=an-1(n≥2,n∈N*),则{an}的通项公式为
_________________.
an=
(1)B (2)an= [(1)a11=a10=a9=a8=…=×…×a1=a1=.故选B.
(2)已知an+1-n=an-1(n≥2,n∈N*),
则an+1-an=n-1,
即n≥3时,an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2
=(n-2)+(n-3)+…+1+2=+2=,
又因为当n=2时,a2=2满足上式,
当n=1时,a1=1不满足上式,
所以an=]
反思领悟 本例(1),an+1=an这一递推关系可化为=的形式,可用累乘法:×…×=×…×,即a11=×a1=, 也可用本例解答中的方法;
本例(2),an+1-an=n-1这一递推关系,一般用累加法求和,但一定要注意能消去多少项,保留多少项.
巩固迁移2 (1)在数列{an}中,a1=2,an+1=an+,则an=________.
(2)若数列{an}满足a1=1,nan-1=(n+1)an(n≥2),则an=_______.
(1)3- (2) [(1)因为当n≥2时,an-an-1==,
所以当n≥2时,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=+…++2=3-.
当n=1时,满足上式.故an=3-.
3-
(2)由nan-1=(n+1)an(n≥2),
得=(n≥2).
所以an=·…··a1=×…××1=,
又因为a1=1也满足上式,所以an=.]
考点三 数列的函数特性
分类标准 类型 满足条件
按项数 分类 有穷数列 项数____
无穷数列 项数____
按项与项间的大小关系分类 递增数列 an+1__an 其中
n∈N*
递减数列 an+1__an
常数列 an+1=an
有限
无限
>
<
分类标准 类型 满足条件
按其他 标准分类 摆动数列 从第2项起,有些项大于它的前一项,有些项小于它的前一项
周期数列 对n∈N*,存在正整数k,使an+k=an
[常用结论] 在数列{an}中,若an最大,则(n≥2),若an最小,则(n≥2).
考向1 数列的周期性
[典例3] (2024·海宁市月考)已知数列{an},a1=4,a2=1,an+2=an+1-an(n∈N*),则a2 025=( )
A.4 B.3
C.-3 D.-4
√
C [因为a1=4,a2=1,an+2=an+1-an(n∈N*),
所以a3=a2-a1=1-4=-3,
a4=a3-a2=-3-1=-4,
a5=a4-a3=-4-(-3)=-1,
a6=a5-a4=-1-(-4)=3,
a7=a6-a5=3-(-1)=4,
a8=a7-a6=4-3=1,
……
所以数列{an}是以6为周期的数列,
所以a2 025=a337×6+3=a3=-3.故选C.]
反思领悟 本例由递推关系a1=4,a2=1,an+2=an+1-an计算出a3,a4,a5,a6,a7,a8,观察并发现数列{an}中,a1,a2,…a6,a7,a8…每6项循环出现一次,故数列{an}的周期为6,进而可求
a2 025.由递推公式计算出一些项,观察并发现周期,是数列求周期的最实用方法.
巩固迁移3 (2024·哈尔滨南岗区月考)若数列{an}满足an+1=,a3=3,则a2 025=( )
A.- B.
C. D.3
√
D [因为an+1=,a3=3,
所以a3==3,解得a2=.
又a2==,解得a1=-.
又a4==-,a5==,a6==3,
显然,接下去a7=-,a8=,a9=3,…,
所以数列{an}是以3为周期的数列,则a2 025=a674×3+3=a3=3.故选D.]
考向2 数列的单调性
[典例4] 已知数列{an}的通项公式为an=,若数列{an}为递减数列,则实数k的取值范围为( )
A.(3,+∞) B.(2,+∞)
C.(1,+∞) D.(0,+∞)
√
D [因为an+1-an==,
由数列{an}为递减数列知,
对于任意的n∈N*,an+1-an=<0,所以k>3-3n对于任意的n∈N*恒成立,所以k∈(0,+∞).故选D.]
反思领悟 数列是特殊的函数,利用数列的单调性求参数实质是函数中的恒成立问题.如本例中,由{an}递减可得an+1-an<0,即k>3-3n恒成立.
巩固迁移4 (2024·秦皇岛月考)已知数列{an}是递增数列,则其通项公式可以是( )
A.an=n2-n B.an=3n-9n
C.an= D.an=3n-1-2n
√
A [对于A,an=n2-n,
则an+1-an=(n+1)2-(n+1)-n2+n=2n>0,是递增数列,A正确;
对于B,an=3n-9n,
则a1=-6,a2=-9,不是递增数列,故B错误;
对于C,an=
则a5=25,a6=13,不是递增数列,故C错误;
对于D,an=3n-1-2n,
则a1=a2=-1,不是递增数列,故D错误.故选A.]
考向3 数列的最值
[典例5] (2024·沈阳期末)已知数列{an}的通项公式为an=,则此数列的最大项为( )
A. B.
C. D.
√
D [法一:an+1-an==,
当n<8时,an+1-an>0,即an+1>an;
当n=8时,an+1-an=0,即an+1=an;
当n>8时,an+1-an<0,即an+1<an,
所以a1<a2<a3<…<a8=a9>a10>a11>…,
所以数列{an}有最大项,为第8项和第9项,且a8=a9==.
法二:设数列{an}的第n项最大,则(n≥2),
即
解得8≤n≤9,又n∈N*,则n=8或n=9,
故数列{an}有最大项,为第8项和第9项,且a8=a9=.
故选D.]
反思领悟 本例法一,求出an+1-an=后,利用函数单调性求{an}的最大项,法二利用(n≥2)确定最大项.
巩固迁移5 (2025·锦州模拟)数列{an}的通项公式为an=,该数列的前50项中最大项是( )
A.a1 B.a44
C.a45 D.a50
√
C [an==
=1+,
因为>0,∈(44,45),
当n≤44时,数列{an}递减,且an<1,
当n≥45时,数列{an}递减,且an>1,
当n=45时,取得最大项.
故选C.]
随堂练习
√
1.(2024·石景山期末)在数列{an}中,a1=-2,an+1=1-(n∈N*),则a2 025的值为( )
A.-2 B.
C. D.
B [由a1=-2,an+1=1-(n∈N*),可得a2=1-=,
a3=1-=,a4=1-3=-2=a1,
a5=1-==a2,…,
即数列{an}是周期为3的数列,
则a2 025=a3×674+3=a3=.
故选B.]
2.(2024·琼海期末)下列四个选项中,不正确的是( )
A.数列的图象是一群孤立的点
B.数列1,0,1,0,…与数列0,1,0,1,…是同一数列
C.数列,…的一个通项公式是an=(n∈N*)
D.数列,…,是递减数列
√
B [根据数列的函数特性可知,数列的图象是一群孤立的点,A正确;
根据数列的定义可知,数列的项具有一定的顺序,B错误;
数列…的一个通项公式是an=,C正确;
根据数列单调性的定义可知,D正确.
故选B.]
3.(2024·唐山二模)已知数列{an}满足an+1=an+a1+2n,a10=130,则a1=( )
A.1 B.2
C.3 D.4
√
D [由an+1=an+a1+2n,可得an+1-an=a1+2n,
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=a1+(a1+2)+(a1+4)+…+(a1+2n-2)
=na1+(n-1)(2+2n-2)=na1+n(n-1),
由a10=130,可得10a1+90=130,解得a1=4.故选D.]
4.(2024·鄂尔多斯期末)已知数列{an}的前n项和Sn=2n,则a3+a4=________.
12 [由数列{an}的前n项和Sn=2n,
可得a3+a4=S4-S2=24-22=12.]
12
【教用·备选题】
1.已知数列{an}满足a1=3,an+1+an=2,则a22=( )
A.3 B.2
C.1 D.-1
√
D [因为数列{an}满足a1=3,an+1+an=2,
所以a1=3,a2=-1,a3=3,a4=-1,…,
故数列{an}是周期为2的数列,所以a22=a2=-1.
故选D.]
2.(2024·南昌月考)已知数列{an}是递增数列,且an=则a的取值范围是( )
A. B.
C. D.
√
D [根据题意,因为数列{an}是递增数列,且an=
所以
解得
3.(2024·茂名一模)数列{an}满足a1=8,an+1=(n∈N*),bn=,若数列{bn}是递减数列,则实数λ的取值范围是
( )
A. B.
C. D.
√
D [由题意an+1=,两边取倒数可化为==+n,即=n,
所以=1,=2,…,=n-1,
由累加法可得=1+2+…+(n-1)=,
因为a1=8,所以==,
所以bn==,
因为数列{bn}是递减数列,故bn<bn-1(n≥2),
所以<,
即λ>=-+1,
因为n≥2且n∈N*,故当n=2或n=3时,+1取得最大值,故λ>.故选D.]
4.(2025·房山区模拟)设Sn为数列{an}的前n项和,且Sn=n2-n,则a5=________;数列{an}的通项公式an=________.
8 2n-2 [由Sn为数列{an}的前n项和,且Sn=n2-n,得
当n=1时,a1=S1=0,
当n≥2时,an=Sn-Sn-1=n2-n-(n-1)2+(n-1)=2n-2,
当n=1时,上式成立,所以an=2n-2,a5=8.]
8
2n-2
5.(2025·湘西州模拟)已知数列{an}的前n项和Sn满足Sn=2an+2,则S5=________.
-62 [令n=1,得a1=S1=2a1+2,所以a1=-2,
Sn=2an+2,当n≥2时,Sn-1=2an-1+2,两式相减得,
Sn-Sn-1=2an-2an-1,即an=2an-2an-1,即=2,
所以数列{an}是首项为-2,公比为2的等比数列,
所以S5==-62.]
-62
6.(2025·湖北武汉模拟)九连环是我国从古至今广泛流传的一种益智游戏,它用九个圆环相连成串,以解开为胜.用an表示解下n(n≤9,n∈N*)个圆环所需的最少移动次数.若a1=1,且an+1=
则解下6个圆环所需的最少移动次数为________.
64 [因为a1=1,所以a2=2a1+2=4,a3=2a2-1=7,a4=2a3+2=16,a5=2a4-1=31,a6=2a5+2=64.]
64
课后习题(三十七) 数列的概念与简单表示法
1.(人教A版选择性必修第二册P8练习T4改编)已知数列{an}的前n项和为Sn,且Sn=3n2+2n,则数列{an}的通项公式为an=________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
6n-1
题号
1
3
5
2
4
6
8
7
9
10
11
12
6n-1 [由题知,Sn=3n2+2n,则Sn-1=3(n-1)2+2(n-1)=3n2-4n+1(n≥2),an=Sn-Sn-1=6n-1(n≥2),又a1=S1=5,符合上式,所以an=6n-1(n∈N*).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版选择性必修第二册P9习题4.1T7改编)设数列{an}的通项公式为an=n2+kn,若数列{an}是递增数列,则实数k的取值范围为___________.
(-3,+∞) [由数列{an}是递增数列,可得an+1>an对于任意的n∈N*恒成立,即(n+1)2+k(n+1)>n2+kn,即2n+1+k>0,即k>
-2n-1对于任意的n∈N*恒成立.因为f (n)=-2n-1(n∈N*)递减,所以f (n)max=f (1)=-3,所以k>-3.]
(-3,+∞)
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(苏教版选择性必修第一册P139习题4.1T8改编)已知数列{an}的通项公式为an=(n∈N*),则数列{an}的最大项为第________项.
4 [法一:因为an+1-an==,
所以当n≥4时,an+1
即a1
故数列{an}的最大项为第4项.
4
题号
1
3
5
2
4
6
8
7
9
10
11
12
法二:设数列{an}中的最大项为ak,则(k≥2),
即解得≤k≤.
因为k∈N*,所以k=4.
故数列{an}的最大项为第4项.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第二册P9习题4.1T4改编)已知数列{an}的前n项和为Sn,a1=,Sn=n2·an,bn=.
(1)写出数列{bn}的前4项;
(2)求出数列{an}的通项公式.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)因为Sn=n2·an,①
所以Sn+1=(n+1)2·an+1,②
②-①,得an+1=(n+1)2·an+1-n2·an,
所以=,所以bn=,
所以b1=,b2=,b3=,b4=.
(2)当n≥2时,由=,得===,…,=,所以·…·=×…×,
即=(n≥2),
又因为a1=,所以an=(n≥2).
当n=1时,a1=满足上式,故an=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2025·开封模拟)已知数列{an}的前n项和为Sn=3n-1,则a5=
( )
A.81 B.162
C.243 D.486
√
B [因为Sn=3n-1,所以a5=S5-S4=35-1-34+1=162.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·辽宁月考)在数列{an}中,若a1=,an+1=2-,则下列数不是{an}中的项的是( )
A.-2 B.-1
C. D.3
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [因为a1=,an+1=2-,
所以a2=2-=,a3=2-=-2,a4=2-=3,
a5=2-=,
所以数列{an}是以4为周期的数列,故-1不是{an}中的项.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·中山市月考)已知n∈N*,下列数列是递增数列的是( )
A.an= B.an=1-2n
C.an=n2 D.an=
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [对于A,an-an-1==-<0,故{an}为递减数列,故A错误;
对于B,an-an-1=-2<0,故{an}为递减数列,故B错误;
对于C,an-an-1=2n-1>0,故{an}为递增数列,故C正确;
对于D,an-an-1==-<0,故{an}为递减数列,故D错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2025·江苏常州模拟)已知数列{an}的前5项依次为2,0,2,0,2,则下列可以作为数列{an}的通项公式的有( )
A.an= B.an=(-1)n+1
C.an=2 D.an=4
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AC [数列{an}的前5项依次为2,0,2,0,2,
经验证,AC选项,显然可以表示,
对于B,当n=1时,a1=0,故B错误;
对于D,当n=2时,a2=2,故D错误.故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·韩城市期末)设数列{an}满足a1++…+=1-,则an=( )
A.1- B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [∵a1++…+=1-,①
∴当n=1时,a1=1-=.
当n≥2时,a1++…+=1-,②
∴①-②,得=1-=,
∴an=.
当n=1时也成立,∴an=.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·遵义月考)下表中的数阵为“森德拉姆筛”,其特点是每行每列都成等差数列.
2 3 4 5 6 7 …
3 5 7 9 11 13 …
4 7 10 13 16 19 …
5 9 13 17 21 25 …
6 11 16 21 26 31 …
7 13 19 25 31 37 …
… … … … … … …
表中对角线上的一列数2,5,10,17,26,37,…构成数列{an},则a985=( )
A.9852-1 B.9852+1
C.9862-1 D.9862+1
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [根据题意,数列{an}的前几项为2,5,10,17,26,37,…,
归纳可得其递推公式为an+1-an=2n+1,a1=2,
所以an-an-1=2n-1,an-1-an-2=2n-3,…,a2-a1=3,
累加得an-a1=3+5+7+…+(2n-1),
所以an-2==n2-1,所以an=n2+1,
故a985=9852+1.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·江苏启东中学月考)若数列{an}的前n项和Sn=n2-10n(n∈N*),则数列{an}的通项公式an=________,数列{nan}中数值最小的项是第________项.
2n-11
3
题号
1
3
5
2
4
6
8
7
9
10
11
12
2n-11 3 [∵Sn=n2-10n,
∴当n≥2时,an=Sn-Sn-1=2n-11,
当n=1时,a1=S1=-9也适合上式.
∴an=2n-11(n∈N*).
令f (n)=nan=n(2n-11)=2n2-11n,
此函数图象的对称轴为直线n=,但n∈N*,
∴当n=3时,f (n)取得最小值.
∴数列{nan}中数值最小的项是第3项.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·四川绵阳调研)已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则数列{an}的通项公式为
an=
______________________.
题号
1
3
5
2
4
6
8
7
9
10
11
12
an= [因为Sn=2an+1,①
a1=1,当n=1时,S1=a1=2a2,所以a2=.
当n≥2时,Sn-1=2an,②
①-②,得an=2an+1-2an,即=(n≥2).
所以当n≥2时,an=a2·=,
故an=]
谢 谢 !
同课章节目录
