《高考快车道》2026版高三一轮总复习数学(基础版)60 第六章 第4课时 数列求和(一) 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)60 第六章 第4课时 数列求和(一) 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:56 | ||
图片预览







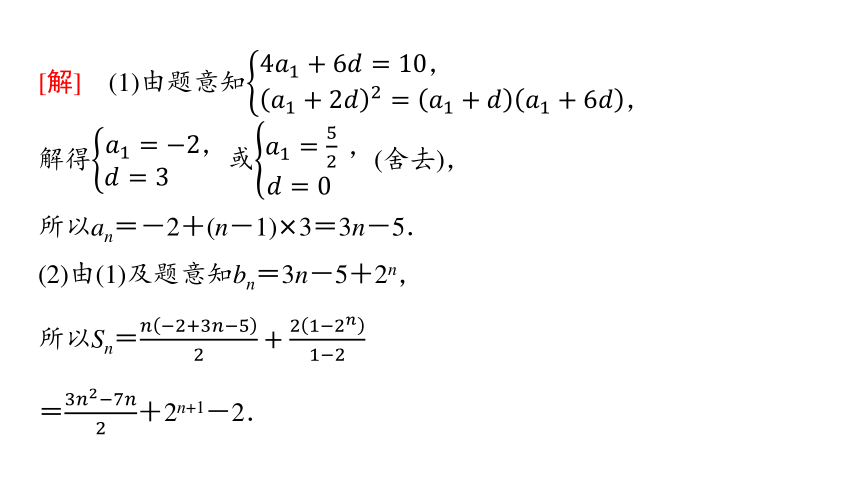


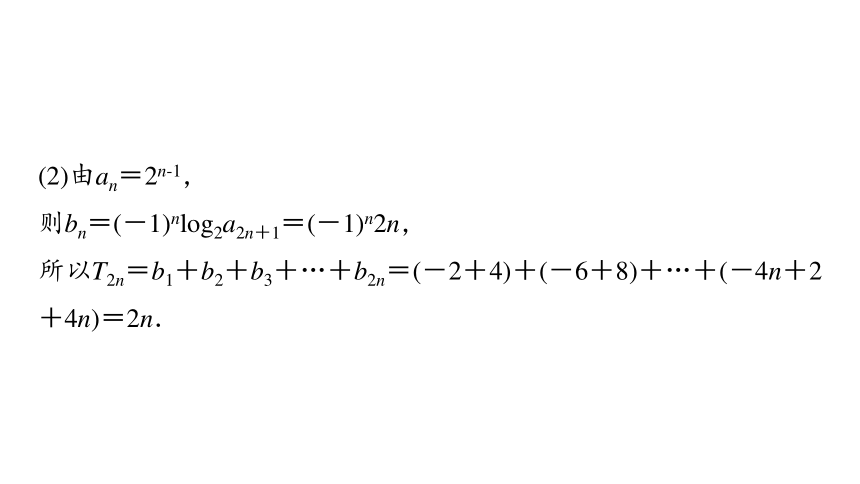

文档简介
(共46张PPT)
第六章 数列
第4课时 数列求和(一)
[考试要求] 1.熟练掌握等差、等比数列的前n项和公式.
2.掌握分组求和、并项求和、倒序相加求和等几种常见的求和方法.
考点一 分组求和
1.等差数列的前n项和公式:Sn==.
2.等比数列的前n项和公式:
Sn=
3.分组求和:若一个数列是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组求和法,分别求和后相加减.
na1+d
[典例1] (2025·安康模拟)记数列{an}的前n项和为Sn,已知an≥1且2Sn=+n.
(1)证明:{an}是等差数列;
(2)记bn=求数列{bn}的前2n项和T2n.
[解] (1)证明:由an≥1且2Sn=+n,
可得2a1=2S1=+1,解得a1=1,
当n≥2时,2an=2Sn-2Sn-1=-(n-1),
即(an-1)2=,
即an-an-1=1或an+an-1=1(舍去),
可得数列{an}是首项和公差均为1的等差数列,即an=n.
(2)由(1)知bn=
则数列{bn}的前2n项和T2n=(b1+b3+…+b2n-1)+(b2+b4+…+b2n)=(2+8+…+22n-1)+(2+4+…+2n)=n(2+2n)=+n+n2.
反思领悟 本例(2)中当n为奇数时,bn=2n为等比数列,当n为偶数时,bn=n为等差数列,可采用分组求和法求和.一般地,通项公式
为an=或an=bn±cn的数列,且{bn},{cn}可求和,
则可采用分组求和法求和.
巩固迁移1 已知公差不为零的等差数列{an}的前4项和为10,且a2,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=an+2n,求数列{bn}的前n项和Sn.
[解] (1)由题意知
解得或(舍去),
所以an=-2+(n-1)×3=3n-5.
(2)由(1)及题意知bn=3n-5+2n,
所以Sn=
=+2n+1-2.
考点二 并项求和
[典例2] (2025·南京模拟)已知等比数列{an}的前n项和为Sn=2n+λ(n∈N*,λ∈R).
(1)求λ的值,并写出数列{an}的通项公式;
(2)若bn=(-1)nlog2a2n+1,求数列{bn}的前2n项和T2n.
[解] (1)由Sn=2n+λ,
知当n=1时,a1=2+λ.
当n≥2时,
an=Sn-Sn-1=2n+λ-2n-1-λ=2n-1.
因为数列{an}为等比数列,
所以a1=2+λ适合an=2n-1,
所以λ=-1,an=2n-1.
(2)由an=2n-1,
则bn=(-1)nlog2a2n+1=(-1)n2n,
所以T2n=b1+b2+b3+…+b2n=(-2+4)+(-6+8)+…+(-4n+2+4n)=2n.
反思领悟 一个数列的前n项和中,可两两或几个相结合求解,则称之为并项求和.形如an=(-1)nf (n)类型,可采用两项合并求解.
巩固迁移2 (2025·银川模拟)数列{an}的通项公式an=n sin ,其前n项和为Sn,则S2 025=________.
[函数y=sin x以6为最小正周期,
又a6m+1+a6m+2+a6m+3+a6m+4+a6m+5+a6m+6=-3,m∈N,
2 025=337×6+3,
所以S2 025=-3×337+2 023sin +2 024·sin +2 025 sin =. ]
考点三 倒序相加求和
[典例3] 设函数f (x)=1+ln ,设a1=1,an=f +f +f +…+f (n∈N*,n≥2).
(1)计算f (x)+f (1-x)的值;
(2)求数列{an}的通项公式.
[解] (1)f (x)+f (1-x)=1+ln +1+ln =2.
(2)由题知,当n≥2时,
an=f +f +f +…+f ,
又an=f +f +…+f ,两式相加得
2an=+…+=2(n-1),所以an=n-1,又a1=1不符合an=n-1,
所以an=
反思领悟 如果一个数列{an}中,与首末两端等“距离”的两项的和相等或等于同一个常数,那么可用倒序相加法求这个数列的前n项和.
巩固迁移3 若f (x)+f (1-x)=4,an=f (0)+f +…+f +
f (1)(n∈N*),则数列{an}的通项公式为___________.
an=2(n+1) [由f (x)+f (1-x)=4,
可得f (0)+f (1)=4,…,f +f =4,所以2an=[f (0)+f (1)]++…+[f (1)+f (0)]=4(n+1),即an=2(n+1).]
an=2(n+1)
随堂练习
√
1.已知数列{an}的通项公式是an=2n-,则其前20项和为( )
A.379+ B.399+
C.419+ D.439+
C [设数列{an}的前n项和为Sn,则S20=a1+a2+a3+…+a20=2(1+2+3+…+20)-=420-=419+.]
2.数列{an}的前n项和为Sn,已知Sn=1-2+3-4+…+
(-1)n-1·n,则S17=________.
9 [∵Sn=1-2+3-4+…+(-1)n-1·n,
∴S17=(1-2)+(3-4)+…+(15-16)+17=-8+17=9.]
9
3.已知函数f (x)满足f (x)=f (1-x),f ′(x)为f (x)的导函数,g(x)=
f ′(x)+,x∈R.若an=g,则数列{an}的前2 025项和为___.
675 [f (x)=f (1-x),
则f ′(x)=-f ′(1-x),即f ′(x)+f ′(1-x)=0,
g(x)=f ′(x)+,x∈R,则g(x)+g(1-x)=f ′(x)+f ′(1-x)+=,
an=g,
675
则a1+a2+…+a2 025=g+g+…+g,
a2 025+…+a2+a1=g+…+g+g,
两式相加可得,a1+a2+…+a2 025==675.
故答案为675.]
【教用·备选题】
1.(2025·东海县模拟)已知数列{an}满足a1=a2=1,an+2=(k∈N*),若Sn为数列{an}的前n项和,则S50=( )
A.624 B.625
C.626 D.650
√
C [依题意,由当n=2k-1时,an+2=an+2,可得当n为奇数时,
an+2-an=2,∵a1=1,∴数列{an}的奇数项是以1为首项,2为公差的等差数列,又当n=2k时,an+2=-an,即当n为偶数时,an+2=
-an,此时an+4=-an+2=-(-an)=an,故数列{an}的偶数项是以2为最小正周期的周期数列,∵a2=1,a4=-a2=-1,∴数列{an}的偶数项为1,-1,1,-1,…,∴S50=a1+a2+…+a50=(a1+a3+…+a49)+(a2+a4+…+a50)=25×1+×2+(1-1+1-1+…+1-1+1)=25+25×24+1=626.
故选C.]
2.(2024·江门期末)已知数列{an}的前n项和为Sn,且Sn=(-1)n+2n+1-,设bn=an-2n,则{bn}的前11项和为( )
A.-1 B.0
C.1 D.2
√
A [由Sn=(-1)n+2n+1-,可得a1=S1=-+4-=1,
当n≥2时,由Sn=(-1)n+2n+1-,
可得Sn-1=(-1)n-1+2n-,
两式相减可得an=Sn-Sn-1=(-1)n+2n,
上式对n=1也成立,则bn=an-2n=(-1)n,
则{bn}的前11项和为-1+1-1+1-…-1+1-1=5×0-1=-1.
故选A.]
课后习题(四十) 数列求和(一)
1.(人教A版选择性必修第二册P51练习T1改编)数列{an}的通项公式an=(-1)n(2n-1),则该数列的前100项和为( )
A.-200 B.-100
C.200 D.100
√
题号
1
3
5
2
4
6
8
7
9
D [S100=(-1+3)+(-5+7)+…+(-197+199)=2×50=100.故选D.]
√
题号
1
3
5
2
4
6
8
7
9
2.(人教A版选择性必修第二册P41习题4.3T7改编)已知数列{an}中,a1=a2=1,an+2=则数列{an}的前20项和为( )
A.1 121 B.1 122
C.1 123 D.1 124
题号
1
3
5
2
4
6
8
7
9
C [由题意可知,数列{a2n}是首项为1,公比为2的等比数列,数列{a2n-1}是首项为1,公差为2的等差数列,故数列{an}的前20项和为+10×1+×2=1 123.故选C.]
题号
1
3
5
2
4
6
8
7
9
3.(人教A版选择性必修第二册P18思考改编)已知函数f (x)=x+sin πx-3,则f+f+f+…+f+f=________.
-8 094
题号
1
3
5
2
4
6
8
7
9
-8 094 [令y=f +f +…+f +f ,①
y=f +f +…+f +f ,②
①+②,得2y=+…+.
因为f (x)+f (2-x)=x+sin πx-3+(2-x)+sin [π(2-x)]-3=-4,
所以2y=-4×4 047,故y=-8 094.]
题号
1
3
5
2
4
6
8
7
9
4.(人教B版选择性必修第三册P55习题5-5AT3改编)已知数列{an}的前n项和为Sn,满足a1=2,且an是2与Sn的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=(-1)n·log2a2n+1,求数列{bn}的前n项和Tn.
题号
1
3
5
2
4
6
8
7
9
[解] (1)因为an是2与Sn的等差中项,所以2an=Sn+2,①
当n≥2时,2an-1=Sn-1+2,②
①-②得2an-2an-1=an,
所以an=2an-1(n≥2),
又因为a1=2,所以{an}是以2为首项,2为公比的等比数列,
所以an=2n.
(2)bn=(-1)n·log2a2n+1=(-1)n·(2n+1),
当n为偶数时,
Tn=(b1+b2)+(b3+b4)+…+(bn-1+bn)=(-3+5)+(-7+9)+…+[-(2n-1)+(2n+1)]=2+2+…+2=2·=n;
当n为奇数时,Tn=b1+(b2+b3)+(b4+b5)+…+(bn-1+bn)=-3+(-2)+(-2)+…+(-2)=-3+(-2)·=-n-2.
综上所述,数列{bn}的前n项和Tn=
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
5.(2025·崇仁县模拟)“数学王子”高斯是近代数学奠基者之一,他的数学研究几乎遍及所有领域,在数论、代数学、非欧几何、复变函数和微分几何等方面都作出了开创性的贡献.我们高中阶段也学习过很多高斯的数学理论,比如高斯函数、倒序相加法、最小二乘法等.已知某数
列的通项an=则a1+a2+…+a51=( )
A.48 B.49 C.50 D.51
√
题号
1
3
5
2
4
6
8
7
9
D [∵当n≠26时,an===1+,
∴an+a52-n=1++1+=2,
∵S=a1+a2+…+a51,
S=a51+a50+…+a1,
∴2S=(a1+a51)+(a2+a50)+…+(a51+a1)=2×51,
∴S=51.故选D.]
题号
1
3
5
2
4
6
8
7
9
6.(多选)(2025·怀仁市模拟)已知数列{an}是等差数列,{bn}是等比数列,a1=1,b1=2,a2+b2=7,a3+b3=13.记cn=
数列{cn}的前n项和为Sn,则( )
A.an=2n-1 B.bn=2n
C.S9=1 409 D.S2n=2n2-n+(4n-1)
√
√
√
题号
1
3
5
2
4
6
8
7
9
ABD [设数列{an}的公差为d,数列{bn}的公比为q(q≠0),
依题意,解得
所以an=2n-1,bn=2n,即选项A,B都正确;
因为cn=
所以c2n-1=a2n-1=4n-3,c2n=b2n=4n,
所以数列{cn}的前2n项和S2n=(a1+a3+…+a2n-1)+(b2+b4+…+b2n)
==2n2-n+(4n-1),
所以S9=S8+a9=2×42-4+(44-1)+17=385,即选项C错误,D正确.故选ABD.]
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
7.(2025·珠海模拟)大衍数列,来源于《乾坤谱》中对《易传》“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理.大衍数列中的每一项都代表太极衍生过程中,曾经经历过的两仪数量的总和.大衍数列从第1项起依次为0,2,4,8,12,18,24,32,40,50,….记大衍数列{an}的通项公式为an=
若bn=(-1)nan,则数列{bn}的前30项和为____.
240
题号
1
3
5
2
4
6
8
7
9
240 [由an=bn=(-1)nan,
可得数列{bn}的前30项和为-a1+a2-a3+a4-…-a29+a30
=--…-
=+…+
=(3+7+11+…+59)+==240.]
题号
1
3
5
2
4
6
8
7
9
8.(2025·浦东模拟)已知数列{an}的前n项和为Sn,Sn=(n2+n),其中n是正整数.
(1)求{an}的通项公式;
(2)数列{bn}满足bn+1=λbn+1,且b1=S1,b2=S2,求数列{bn}的前n项和Hn.
题号
1
3
5
2
4
6
8
7
9
[解] (1)当n≥2时,an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=n,当n=1时,a1=S1=1,满足上式,所以an=n.
(2)依题意,b1=S1=1,b2=S2=3,由bn+1=λ bn+1,得3=λ+1,解得λ=2,则bn+1=2bn+1,即bn+1+1=2(bn+1),而b1+1=2,
因此数列{bn+1}是首项为2,公比为2的等比数列,
则bn+1=2n,即bn=2n-1,
所以数列{bn}的前n项和Hn=-n=2n+1-n-2.
题号
1
3
5
2
4
6
8
7
9
9.已知函数f (x)=(x∈R),正项等比数列{an}满足a50=1,求
f (ln a1)+f (ln a2)+…+f (ln a99).
[解] 因为f (x)=,
所以f (x)+f (-x)===1.
因为数列{an}是等比数列,所以a1a99=a2a98=…=a49a51==1,
即ln a1+ln a99=ln a2+ln a98=…=ln a49+ln a51=2ln a50=0.
题号
1
3
5
2
4
6
8
7
9
所以f (ln a1)+f (ln a99)=f (ln a2)+f (ln a98)=…=f (ln a49)+f (ln a51)=2f (ln a50)=1,
设S99=f (ln a1)+f (ln a2)+f (ln a3)+…+f (ln a99),①
又S99=f (ln a99)+f (ln a98)+f (ln a97)+…+f (ln a1),②
①+②,得2S99=99,
所以S99=.
谢 谢 !
第六章 数列
第4课时 数列求和(一)
[考试要求] 1.熟练掌握等差、等比数列的前n项和公式.
2.掌握分组求和、并项求和、倒序相加求和等几种常见的求和方法.
考点一 分组求和
1.等差数列的前n项和公式:Sn==.
2.等比数列的前n项和公式:
Sn=
3.分组求和:若一个数列是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组求和法,分别求和后相加减.
na1+d
[典例1] (2025·安康模拟)记数列{an}的前n项和为Sn,已知an≥1且2Sn=+n.
(1)证明:{an}是等差数列;
(2)记bn=求数列{bn}的前2n项和T2n.
[解] (1)证明:由an≥1且2Sn=+n,
可得2a1=2S1=+1,解得a1=1,
当n≥2时,2an=2Sn-2Sn-1=-(n-1),
即(an-1)2=,
即an-an-1=1或an+an-1=1(舍去),
可得数列{an}是首项和公差均为1的等差数列,即an=n.
(2)由(1)知bn=
则数列{bn}的前2n项和T2n=(b1+b3+…+b2n-1)+(b2+b4+…+b2n)=(2+8+…+22n-1)+(2+4+…+2n)=n(2+2n)=+n+n2.
反思领悟 本例(2)中当n为奇数时,bn=2n为等比数列,当n为偶数时,bn=n为等差数列,可采用分组求和法求和.一般地,通项公式
为an=或an=bn±cn的数列,且{bn},{cn}可求和,
则可采用分组求和法求和.
巩固迁移1 已知公差不为零的等差数列{an}的前4项和为10,且a2,a3,a7成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=an+2n,求数列{bn}的前n项和Sn.
[解] (1)由题意知
解得或(舍去),
所以an=-2+(n-1)×3=3n-5.
(2)由(1)及题意知bn=3n-5+2n,
所以Sn=
=+2n+1-2.
考点二 并项求和
[典例2] (2025·南京模拟)已知等比数列{an}的前n项和为Sn=2n+λ(n∈N*,λ∈R).
(1)求λ的值,并写出数列{an}的通项公式;
(2)若bn=(-1)nlog2a2n+1,求数列{bn}的前2n项和T2n.
[解] (1)由Sn=2n+λ,
知当n=1时,a1=2+λ.
当n≥2时,
an=Sn-Sn-1=2n+λ-2n-1-λ=2n-1.
因为数列{an}为等比数列,
所以a1=2+λ适合an=2n-1,
所以λ=-1,an=2n-1.
(2)由an=2n-1,
则bn=(-1)nlog2a2n+1=(-1)n2n,
所以T2n=b1+b2+b3+…+b2n=(-2+4)+(-6+8)+…+(-4n+2+4n)=2n.
反思领悟 一个数列的前n项和中,可两两或几个相结合求解,则称之为并项求和.形如an=(-1)nf (n)类型,可采用两项合并求解.
巩固迁移2 (2025·银川模拟)数列{an}的通项公式an=n sin ,其前n项和为Sn,则S2 025=________.
[函数y=sin x以6为最小正周期,
又a6m+1+a6m+2+a6m+3+a6m+4+a6m+5+a6m+6=-3,m∈N,
2 025=337×6+3,
所以S2 025=-3×337+2 023sin +2 024·sin +2 025 sin =. ]
考点三 倒序相加求和
[典例3] 设函数f (x)=1+ln ,设a1=1,an=f +f +f +…+f (n∈N*,n≥2).
(1)计算f (x)+f (1-x)的值;
(2)求数列{an}的通项公式.
[解] (1)f (x)+f (1-x)=1+ln +1+ln =2.
(2)由题知,当n≥2时,
an=f +f +f +…+f ,
又an=f +f +…+f ,两式相加得
2an=+…+=2(n-1),所以an=n-1,又a1=1不符合an=n-1,
所以an=
反思领悟 如果一个数列{an}中,与首末两端等“距离”的两项的和相等或等于同一个常数,那么可用倒序相加法求这个数列的前n项和.
巩固迁移3 若f (x)+f (1-x)=4,an=f (0)+f +…+f +
f (1)(n∈N*),则数列{an}的通项公式为___________.
an=2(n+1) [由f (x)+f (1-x)=4,
可得f (0)+f (1)=4,…,f +f =4,所以2an=[f (0)+f (1)]++…+[f (1)+f (0)]=4(n+1),即an=2(n+1).]
an=2(n+1)
随堂练习
√
1.已知数列{an}的通项公式是an=2n-,则其前20项和为( )
A.379+ B.399+
C.419+ D.439+
C [设数列{an}的前n项和为Sn,则S20=a1+a2+a3+…+a20=2(1+2+3+…+20)-=420-=419+.]
2.数列{an}的前n项和为Sn,已知Sn=1-2+3-4+…+
(-1)n-1·n,则S17=________.
9 [∵Sn=1-2+3-4+…+(-1)n-1·n,
∴S17=(1-2)+(3-4)+…+(15-16)+17=-8+17=9.]
9
3.已知函数f (x)满足f (x)=f (1-x),f ′(x)为f (x)的导函数,g(x)=
f ′(x)+,x∈R.若an=g,则数列{an}的前2 025项和为___.
675 [f (x)=f (1-x),
则f ′(x)=-f ′(1-x),即f ′(x)+f ′(1-x)=0,
g(x)=f ′(x)+,x∈R,则g(x)+g(1-x)=f ′(x)+f ′(1-x)+=,
an=g,
675
则a1+a2+…+a2 025=g+g+…+g,
a2 025+…+a2+a1=g+…+g+g,
两式相加可得,a1+a2+…+a2 025==675.
故答案为675.]
【教用·备选题】
1.(2025·东海县模拟)已知数列{an}满足a1=a2=1,an+2=(k∈N*),若Sn为数列{an}的前n项和,则S50=( )
A.624 B.625
C.626 D.650
√
C [依题意,由当n=2k-1时,an+2=an+2,可得当n为奇数时,
an+2-an=2,∵a1=1,∴数列{an}的奇数项是以1为首项,2为公差的等差数列,又当n=2k时,an+2=-an,即当n为偶数时,an+2=
-an,此时an+4=-an+2=-(-an)=an,故数列{an}的偶数项是以2为最小正周期的周期数列,∵a2=1,a4=-a2=-1,∴数列{an}的偶数项为1,-1,1,-1,…,∴S50=a1+a2+…+a50=(a1+a3+…+a49)+(a2+a4+…+a50)=25×1+×2+(1-1+1-1+…+1-1+1)=25+25×24+1=626.
故选C.]
2.(2024·江门期末)已知数列{an}的前n项和为Sn,且Sn=(-1)n+2n+1-,设bn=an-2n,则{bn}的前11项和为( )
A.-1 B.0
C.1 D.2
√
A [由Sn=(-1)n+2n+1-,可得a1=S1=-+4-=1,
当n≥2时,由Sn=(-1)n+2n+1-,
可得Sn-1=(-1)n-1+2n-,
两式相减可得an=Sn-Sn-1=(-1)n+2n,
上式对n=1也成立,则bn=an-2n=(-1)n,
则{bn}的前11项和为-1+1-1+1-…-1+1-1=5×0-1=-1.
故选A.]
课后习题(四十) 数列求和(一)
1.(人教A版选择性必修第二册P51练习T1改编)数列{an}的通项公式an=(-1)n(2n-1),则该数列的前100项和为( )
A.-200 B.-100
C.200 D.100
√
题号
1
3
5
2
4
6
8
7
9
D [S100=(-1+3)+(-5+7)+…+(-197+199)=2×50=100.故选D.]
√
题号
1
3
5
2
4
6
8
7
9
2.(人教A版选择性必修第二册P41习题4.3T7改编)已知数列{an}中,a1=a2=1,an+2=则数列{an}的前20项和为( )
A.1 121 B.1 122
C.1 123 D.1 124
题号
1
3
5
2
4
6
8
7
9
C [由题意可知,数列{a2n}是首项为1,公比为2的等比数列,数列{a2n-1}是首项为1,公差为2的等差数列,故数列{an}的前20项和为+10×1+×2=1 123.故选C.]
题号
1
3
5
2
4
6
8
7
9
3.(人教A版选择性必修第二册P18思考改编)已知函数f (x)=x+sin πx-3,则f+f+f+…+f+f=________.
-8 094
题号
1
3
5
2
4
6
8
7
9
-8 094 [令y=f +f +…+f +f ,①
y=f +f +…+f +f ,②
①+②,得2y=+…+.
因为f (x)+f (2-x)=x+sin πx-3+(2-x)+sin [π(2-x)]-3=-4,
所以2y=-4×4 047,故y=-8 094.]
题号
1
3
5
2
4
6
8
7
9
4.(人教B版选择性必修第三册P55习题5-5AT3改编)已知数列{an}的前n项和为Sn,满足a1=2,且an是2与Sn的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=(-1)n·log2a2n+1,求数列{bn}的前n项和Tn.
题号
1
3
5
2
4
6
8
7
9
[解] (1)因为an是2与Sn的等差中项,所以2an=Sn+2,①
当n≥2时,2an-1=Sn-1+2,②
①-②得2an-2an-1=an,
所以an=2an-1(n≥2),
又因为a1=2,所以{an}是以2为首项,2为公比的等比数列,
所以an=2n.
(2)bn=(-1)n·log2a2n+1=(-1)n·(2n+1),
当n为偶数时,
Tn=(b1+b2)+(b3+b4)+…+(bn-1+bn)=(-3+5)+(-7+9)+…+[-(2n-1)+(2n+1)]=2+2+…+2=2·=n;
当n为奇数时,Tn=b1+(b2+b3)+(b4+b5)+…+(bn-1+bn)=-3+(-2)+(-2)+…+(-2)=-3+(-2)·=-n-2.
综上所述,数列{bn}的前n项和Tn=
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
5.(2025·崇仁县模拟)“数学王子”高斯是近代数学奠基者之一,他的数学研究几乎遍及所有领域,在数论、代数学、非欧几何、复变函数和微分几何等方面都作出了开创性的贡献.我们高中阶段也学习过很多高斯的数学理论,比如高斯函数、倒序相加法、最小二乘法等.已知某数
列的通项an=则a1+a2+…+a51=( )
A.48 B.49 C.50 D.51
√
题号
1
3
5
2
4
6
8
7
9
D [∵当n≠26时,an===1+,
∴an+a52-n=1++1+=2,
∵S=a1+a2+…+a51,
S=a51+a50+…+a1,
∴2S=(a1+a51)+(a2+a50)+…+(a51+a1)=2×51,
∴S=51.故选D.]
题号
1
3
5
2
4
6
8
7
9
6.(多选)(2025·怀仁市模拟)已知数列{an}是等差数列,{bn}是等比数列,a1=1,b1=2,a2+b2=7,a3+b3=13.记cn=
数列{cn}的前n项和为Sn,则( )
A.an=2n-1 B.bn=2n
C.S9=1 409 D.S2n=2n2-n+(4n-1)
√
√
√
题号
1
3
5
2
4
6
8
7
9
ABD [设数列{an}的公差为d,数列{bn}的公比为q(q≠0),
依题意,解得
所以an=2n-1,bn=2n,即选项A,B都正确;
因为cn=
所以c2n-1=a2n-1=4n-3,c2n=b2n=4n,
所以数列{cn}的前2n项和S2n=(a1+a3+…+a2n-1)+(b2+b4+…+b2n)
==2n2-n+(4n-1),
所以S9=S8+a9=2×42-4+(44-1)+17=385,即选项C错误,D正确.故选ABD.]
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
7.(2025·珠海模拟)大衍数列,来源于《乾坤谱》中对《易传》“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理.大衍数列中的每一项都代表太极衍生过程中,曾经经历过的两仪数量的总和.大衍数列从第1项起依次为0,2,4,8,12,18,24,32,40,50,….记大衍数列{an}的通项公式为an=
若bn=(-1)nan,则数列{bn}的前30项和为____.
240
题号
1
3
5
2
4
6
8
7
9
240 [由an=bn=(-1)nan,
可得数列{bn}的前30项和为-a1+a2-a3+a4-…-a29+a30
=--…-
=+…+
=(3+7+11+…+59)+==240.]
题号
1
3
5
2
4
6
8
7
9
8.(2025·浦东模拟)已知数列{an}的前n项和为Sn,Sn=(n2+n),其中n是正整数.
(1)求{an}的通项公式;
(2)数列{bn}满足bn+1=λbn+1,且b1=S1,b2=S2,求数列{bn}的前n项和Hn.
题号
1
3
5
2
4
6
8
7
9
[解] (1)当n≥2时,an=Sn-Sn-1=(n2+n)-[(n-1)2+(n-1)]=n,当n=1时,a1=S1=1,满足上式,所以an=n.
(2)依题意,b1=S1=1,b2=S2=3,由bn+1=λ bn+1,得3=λ+1,解得λ=2,则bn+1=2bn+1,即bn+1+1=2(bn+1),而b1+1=2,
因此数列{bn+1}是首项为2,公比为2的等比数列,
则bn+1=2n,即bn=2n-1,
所以数列{bn}的前n项和Hn=-n=2n+1-n-2.
题号
1
3
5
2
4
6
8
7
9
9.已知函数f (x)=(x∈R),正项等比数列{an}满足a50=1,求
f (ln a1)+f (ln a2)+…+f (ln a99).
[解] 因为f (x)=,
所以f (x)+f (-x)===1.
因为数列{an}是等比数列,所以a1a99=a2a98=…=a49a51==1,
即ln a1+ln a99=ln a2+ln a98=…=ln a49+ln a51=2ln a50=0.
题号
1
3
5
2
4
6
8
7
9
所以f (ln a1)+f (ln a99)=f (ln a2)+f (ln a98)=…=f (ln a49)+f (ln a51)=2f (ln a50)=1,
设S99=f (ln a1)+f (ln a2)+f (ln a3)+…+f (ln a99),①
又S99=f (ln a99)+f (ln a98)+f (ln a97)+…+f (ln a1),②
①+②,得2S99=99,
所以S99=.
谢 谢 !
同课章节目录
