《高考快车道》2026版高三一轮总复习数学(基础版)59 第六章 第3课时 等比数列 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)59 第六章 第3课时 等比数列 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:56 | ||
图片预览




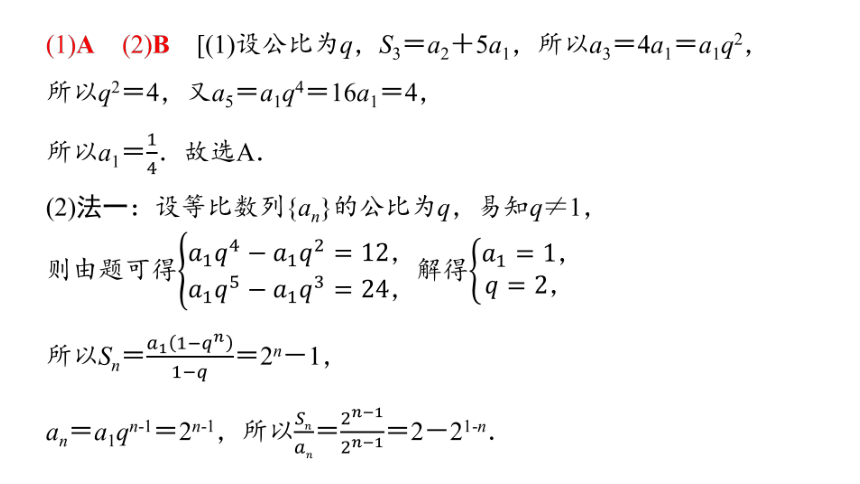







文档简介
(共77张PPT)
第六章 数列
第3课时 等比数列
[考试要求] 1.理解等比数列的概念.
2.掌握等比数列的通项公式与前n项和公式.
3.了解等比数列与指数函数的关系.
考点一 等比数列基本量的运算
1.通项公式:an=____________=amqn-m.
2.前n项和公式:Sn=
提醒:(1)求等比数列前n项和时,若公比q不明确,需分类讨论.
(2)当q≠1时,等比数列{an}的前n项和Sn=A+B·Cn A+B=0,公比q=C(A,B,C均不为零).
a1qn-1
na1(q=1)
(q≠1)
[典例1] (1)(2024·盐城一模)等比数列{an}的前n项和为Sn,已知S3=a2+5a1,a5=4,则a1=( )
A. B.-
C. D.-
(2)记Sn为等比数列{an}的前n项和.若a5-a3=12,a6-a4=24,则等于( )
A.2n-1 B.2-21-n
C.2-2n-1 D.21-n-1
√
√
(1)A (2)B [(1)设公比为q,S3=a2+5a1,所以a3=4a1=a1q2,
所以q2=4,又a5=a1q4=16a1=4,
所以a1=.故选A.
(2)法一:设等比数列{an}的公比为q,易知q≠1,
则由题可得解得
所以Sn==2n-1,
an=a1qn-1=2n-1,所以==2-21-n.
法二:设等比数列{an}的公比为q,易知q≠1,
因为====2,
所以q=2,所以===2-21-n.]
反思领悟 (1)等比数列的通项公式an=a1qn-1与前n项和公式Sn==(q≠1)中共涉及五个量a1,an,q,n,Sn.已知其中三个就能求另外两个(简称“知三求二”).
(2)等比数列的前n项和公式涉及对公比q的分类讨论,当q=1时,{an}的前n项和Sn=na1;当q≠1时,{an}的前n项和Sn==.
巩固迁移1 (1)(2025·徐州模拟)已知数列{an}为等比数列,a2=6,6a1+a3=30,则a4=________.
(2)(2023·全国甲卷)记Sn为等比数列{an}的前n项和.若8S6=7S3,则{an}的公比为________.
(1)54或24 (2)- [(1)由
解得或
a4=a1·q3=2×33=54或a4=3×23=24.
54或24
-
(2)若q=1,则由8S6=7S3得8×6a1=7×3a1,则a1=0,不合题意,所以q≠1.
当q≠1时,因为8S6=7S3,
所以=,
即8(1-q6)=7(1-q3),
即8(1+q3)(1-q3)=7(1-q3),即8(1+q3)=7,
解得q=-.]
考点二 等比数列的判定与证明
1.等比数列的定义:一般地,如果一个数列从第__项起,每一项与它的前一项的比都等于__________(不为零),那么这个数列叫做等比数列.这个常数叫做等比数列的____,通常用字母q表示,定义的表达式为=q(n∈N*,q为非零常数).
2.等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么____叫做a与b的等比中项,此时,G2=ab.
提醒:“G2=ab”是“a,G,b成等比数列”的必要不充分条件.
2
同一个常数
公比
G
[典例2] (2025·八省联考节选)已知数列{an}中,a1=3,an+1=.
(1)证明:数列为等比数列;
(2)求{an}的通项公式.
[解] (1)证明:因为an+1=,a1=3>0,
所以an>0,所以==,
所以1-==.
因为1-=≠0,
所以数列是以为首项,为公比的等比数列.
(2)由(1)知,1-==,
所以=1-,所以an==.
反思领悟 通常用定义法证明一个数列为等比数列.即=q(q≠0).本例只需证明=≠0.
巩固迁移2 已知数列{an}中,a1=2,且an=2an-1-n+2(n≥2,n∈N*).
(1)求a2,a3,并证明{an-n}是等比数列;
(2)求通项公式an.
[解] (1)由a1=2,an=2an-1-n+2(n≥2,n∈N*),
得a2=2a1-2+2=4,a3=2a2-3+2=7,
∵an-n=2an-1-2n+2=2[an-1-(n-1)],
∴=2(n≥2,n∈N*),
又∵a1-1=1,
∴{an-n}是首项为1,公比为2的等比数列.
(2)由(1)知an-n=1×2n-1,
∴an=2n-1+n.
考点三 等比数列的性质
1.等比数列的常用性质
(1)若m+n=p+q,则__________________,其中m,n,p,q∈N*.特别地,若2w=m+n,则__________,其中m,n,w∈N*.
(2)ak,ak+m,ak+2m,…仍是等比数列,公比为____(k,m∈N*).
(3)若数列{an},{bn}是两个项数相同的等比数列,则数列{ban},{pan·qbn}和也是等比数列(b,p,q≠0).
am·an=ap·aq
=am·an
qm
(4)若或则等比数列{an}递____.
若或则等比数列{an}递____.
增
减
2.等比数列前n项和的常用性质
若等比数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn,q=-1且n为偶数时除外.
提醒:(1)由an+1=qan,q≠0,并不能断定{an}为等比数列,还要验证a1≠0.
(2)等比数列的前n项和Sn==qn,令A=-,可以写成Sn=Aqn-A(其中A≠0,q≠1).
[常用结论]
1.数列{an}是等比数列.
(1)若a1·a2·…·an=Tn,则Tn,,…成等比数列.
(2)若Sn是其前n项和,数列{an}的项数为2n,则=q;若项数为2n+1,则=q或=q.
2.三个数成等比数列,通常设为,x,xq;四个符号相同的数成等比数列,通常设为,xq,xq3.
考向1 项的性质
[典例3] 已知数列{an}是等比数列,若a2,a48是方程2x2-7x+6=0的两个根,则a1·a2·a25·a48·a49的值为( )
A. B.9
C.±9 D.243
√
C [若a2,a48是2x2-7x+6=0的两个根,
则a2+a48=,a2·a48==3,
因为数列{an}是等比数列,a2·a48==3,
所以a25=±,a1·a2·a25·a48·a49==±9.故选C.]
反思领悟 在等比数列中,两项之积可转化为另外两项之积或某项的平方,通过本例要树立这一“转化意识”.
巩固迁移3 (2023·全国乙卷)已知{an}为等比数列,a2a4a5=a3a6,a9a10=-8,则a7=________.
-2 [法一:设数列{an}的公比为q,则由a2a4a5=a3a6,得a1q·a1q3·a1q4=a1q2·a1q5.又因为a1≠0,且q≠0,所以可得a1q=1.①
又因为a9a10=a1q8·a1q9=q17=-8,②
所以由①②可得q15=-8,q5=-2,所以a7=a1q6=a1q·q5=-2.
-2
法二:设数列{an}的公比为q.因为a4a5=a3a6≠0,所以a2=1.
又因为a9a10=a2q7·a2q8=q15=-8,于是q5=-2,所以a7=a2q5=-2.]
考向2 和的性质
[典例4] (2023·新高考Ⅱ卷)记Sn为等比数列{an}的前n项和,若S4=-5,S6=21S2,则S8=( )
A.120 B.85
C.-85 D.-120
√
C [法一:设等比数列{an}的公比为q(q≠0),由题意易知q≠1,则
化简整理得
所以S8==×(1-44)=-85.故选C.
法二:易知S2,S4-S2,S6-S4,S8-S6,…为等比数列,所以(S4-S2)2=S2·(S6-S4),解得S2=-1或S2=.当S2=-1时,由(S6-S4)2=(S4-S2)·(S8-S6),解得S8=-85;当S2=时,结合S4=-5得
化简可得q2=-5,不成立,舍去.
所以S8=-85.故选C.]
反思领悟 本例方法一关键是把和q2都“整体看待”,减少了运算量.方法二利用在等比数列中,S2,S4-S2,S6-S4,S8-S6,…仍为等比数列,但求出S2后,要注意检验.
巩固迁移4 (1)(2025·山西大同模拟)已知等比数列{an}共有2n项,其和为-240,且奇数项的和比偶数项的和大80,则公比q=________.
(2)(人教A版选择性必修第二册P37例9改编)设等比数列{an}的前n项和为Sn,若=3,则=________.
2
(1)2 (2) [(1)由题意,得
解得所以q===2.
(2)设等比数列{an}的公比为q,易知q≠-1,由等比数列前n项和的性质可知S3,S6-S3,S9-S6仍成等比数列,
∴=,又由已知得S6=3S3,
∴S9-S6=4S3,∴S9=7S3,∴=.]
随堂练习
√
1.(2025·周口市川汇区模拟)在等比数列{an}中,a1,a8是方程3x2+2x-6=0的两个根,则a4·a5=( )
A.-6 B.-2
C.- D.2
B [∵在等比数列{an}中,a1,a8是方程3x2+2x-6=0的两个根,
∴a4a5=a1a8=-=-2.故选B.]
2.(多选)(2025·太原模拟)设等比数列{an}的公比为q,则下列结论正确的是( )
A.数列{anan+1}是公比为q2的等比数列
B.数列{an+an+1}是公比为q的等比数列
C.数列{an-an+1}是公比为q的等比数列
D.数列是公比为的等比数列
√
√
AD [对于A,由=q2(n≥2)知数列{anan+1}是公比为q2的等比数列;对于B,当q=-1时,数列{an+an+1}的项中有0,不是等比数列;对于C,当q=1时,数列{an-an+1}的项中有0,不是等比数列;对于D,==,所以数列是公比为的等比数列.故选AD.]
3.(2024·东北三校联考)已知数列{an}为等比数列,其前n项和为Sn,若a2a6=-2a7,S3=-6,则a6等于( )
A.-2或32 B.-2或64
C.2或-32 D.2或-64
√
B [数列{an}为等比数列,
a2a6=-2a7=a1a7,解得a1=-2,
设数列{an}的公比为q,则S3=-6=-2-2q-2q2,
解得q=-2或q=1,
当q=-2时,a6=(-2)6=64,
当q=1时,a6=-2.故选B.]
4.在等比数列{an}中,已知a1a3=36,a2+a4=60,则a1+q=________.
±5 [设等比数列{an}的首项为a1,公比为q,由等比数列的性质得a1a3==36,又因为a2+a4=a2(1+q2)=60,所以a2>0,a2=6,所以1+q2=10,解得q=±3.当q=3时,由a2=a1q=6,可得a1=2;当q=-3时,由a2=a1q=6,可得a1=-2,
所以或则a1+q=±5.]
±5
【教用·备选题】
1.(2025·中山市模拟)数列{an}满足an+1=,a1=,若an=,则项数n为( )
A.3 B.4
C.5 D.6
√
C [因为数列{an}满足an+1=an,a1=,
所以数列{an}是以为首项,为公比的等比数列,若an==,
则项数n=5.
故选C.]
2.(2025·衡阳模拟)已知{an}是等比数列,且a6-a4=-24,a7-a5=48,则a1=( )
A.-1 B.
C.1 D.2
√
C [因为{an}是等比数列,且a6-a4=a4(q2-1)=-24,a7-a5=a5(q2-1)=48,
两式相除可得,=q=-2,
所以a6-a4=a1(q5-q3)=-24a1=-24,
所以a1=1.
故选C.]
3.(2025·贵阳模拟)设等比数列{an}的前n项和为Sn,a2+a4=5,a3+a5=10,则S6=( )
A. B.63
C. D.31
√
A [设等比数列{an}的公比为q,∵a2+a4=5,a3+a5=10,
∴q(a2+a4)=5q=10,a1q2(1+q2)=10,
联立解得a1=,q=2,则S6==.
故选A.]
4.(多选)(2025·南阳模拟)若数列{an}是等比数列,且an>0(n∈N*),则下列结论正确的是( )
A.数列}是等比数列
B.数列{an+1-an}是等比数列
C.数列{a2n}是等比数列
D.数列{lg an}是等比数列
√
√
AC [设等比数列{an}的公比为q,因为an>0(n∈N*),所以q>0,
对于==q2,所以数列是等比数列,故A正确;
对于B,当q=1时,等比数列{an}为正项常数列,此时an+1-an=0,所以数列{an+1-an}不是等比数列,故B错误;
对于C,==q2,所以数列{a2n}是等比数列,故C正确;
对于D,若an=1,则lg an=0,所以数列{lg an}不是等比数列,故D错误.
故选AC.]
5.(2025·辽宁模拟)已知等比数列{an}的前n项和为Sn,a1=,8S6=7S3,若λ≥Sn恒成立,则λ的最小值为( )
A. B.
C. D.1
√
C [设等比数列{an}的公比为q,由8S6=7S3,得8(S6-S3)=-S3,
则a4+a5+a6=-(a1+a2+a3),即q3(a1+a2+a3)=-(a1+a2+a3),因为an≠0,所以q3=-,解得q=-,又因为a1=,所以an=,所以Sn==,
当n为奇数时,Sn=,所以Sn≤S1=,
当n为偶数时,Sn=<,所以(Sn)max=,所以λ≥.
故选C.]
6.(2025·黄山模拟)等比数列{an}的前n项和为Sn,前n项积为Tn,a4-a2=6,a5-a3=12,当最小时,n的值为( )
A.3 B.4
C.5 D.6
√
C [因为{an}是等比数列,所以=q==2,
又因为a4-a2=6=a2(q2-1)=3a2,a2=2,
所以a1=1,an=2n-1,
Tn=20×21×22×…×2n-1=20+1+2+…+(n-1)=,
Sn==2n-1,==,
因为y=2t在R上单调递增,t=的图象开口向上,当n=5时取最小值,所以当n=5时, 取最小值.
故选C.]
7.(多选)(2025·长沙模拟)设等比数列{an}的公比为q,前n项积为Tn,下列说法正确的是( )
A.若T8=T12,则a10a11=1
B.若T8=T12,则T20=1
C.若a1=1 024,且T10为数列{Tn}的唯一最大项,则D.若a1>0,且T10>T11>T9,则使得Tn>1成立的n的最大值为20
√
√
√
BCD [对于A,若T8=T12,则有=a9a10a11·a12=1,
结合a9a12=a10a11,可得a10a11=±1,故A不正确;
对于B,若T8=T12,则有=a9a10a11a12=1,
可知T20=a1a2a3a4…a17a18a19a20=(a9a10a11·a12)5=1,B正确;
对于C,若a1=1 024,且T10为数列{Tn}的唯一最大项,
则公比q>0,a10>1且a11<1,即解得对于D,若a1>0,且T10>T11>T9,
则q>0,<1且>1,即a11<1,a10a11>1,可知0<q<1,
由此得到T20=(a10a11)10>1,T21=<1,当n≥21时,Tn均小于1.
综上所述,使得Tn>1成立的n的最大值为20,故D正确.故选BCD.]
8.已知正项等比数列{an}的前n项和为Sn,且S8-2S4=5,则a9+a10+a11+a12的最小值为( )
A.10 B.15
C.20 D.25
√
C [由题意可得a9+a10+a11+a12=S12-S8,
由S8-2S4=5,可得S8-S4=S4+5.
又由等比数列的性质知S4,S8-S4,S12-S8成等比数列,
则S4(S12-S8)=(S8-S4)2.
于是a9+a10+a11+a12=S12-S8==S4++10≥2+10=20,
当且仅当S4=5时等号成立.
所以a9+a10+a11+a12的最小值为20.故选C.]
9.(2025·韩城市模拟)已知等比数列{an}的前n项和为Sn,公比q>1,若a2=8,S3=28.
(1)求{an}的通项公式;
(2)证明:>Sn+7.
[解] (1)等比数列{an}中,由于a2=8,S3=28,
则有
解得或(舍去),所以an=a1qn-1=2n+1.
(2)证明:因为Sn==2×2n+1-4,且n∈N*,
所以-Sn-7=(2n+1)2-2×2n+1-3=(2n+1-3)(2n+1+1)>0,
所以>Sn+7.
课后习题(三十九) 等比数列
1.(湘教版选择性必修第一册P26例1改编)在等比数列{an}中,a3=2,a7=8,则a5等于( )
A.5 B.±5 C.4 D.±4
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [∵=a3a7=2×8=16,∴a5=±4.
又∵a5=a3q2>0,∴a5=4.故选C.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版选择性必修第二册P37练习T1(3)改编)在等比数列{an}中,a3=,S3=,则a2的值为( )
A. B.-3
C.- D.-3或
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由S3=a1+a2+a3=a3(q-2+q-1+1),得
q-2+q-1+1=3,即2q2-q-1=0,
解得q=1或q=-.
∴a2==或-3.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教A版选择性必修第二册P34练习T3改编)朱载堉是中国明代一位杰出的音乐家、律学家和历学家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度十三个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为f1,第七个音的频率为f2,则=( )
A.4 B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [依题意,十三个音的频率依次成等比数列,记为{an},设公比为q,则a13=a1q12,又∵a13=2a1,
∴q=,∴==q4=()4=.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第二册P41习题4.3T7(1)改编)已知正项数列{an}的前n项积为Tn,且满足an=(n∈N*).求证:数列为等比数列.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[证明] ∵an=,且an=(n≥2),
∴=(n≥2),∵an>0,∴Tn>0,∴3Tn-1=Tn-1(n≥2),
则Tn-=(n≥2),
当n=1时,a1=T1=,得T1=,
∴T1-=,∴数列是首项为,公比为的等比数列.
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·秦皇岛三模)已知等比数列{an}的前n项和为Sn,满足a4+a5+a6=351,S6=364,则数列{an}的公比为( )
A. B.2
C.3 D.4
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [设等比数列{an}的公比为q(q≠0),
∵a1+a2+a3=S6-(a4+a5+a6)=364-351=13,
∴==27=q3,∴q=3.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·吕梁期末)已知正项等比数列{an}满足a4=16,a6=64,则S5=( )
A.62 B.30或10
C.62或-22 D.30
√
A [设正项等比数列{an}的公比为q(q>0),
则q2===4,解得q=2(负值舍去),
故a1==2,则S5==62.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2025·烟台模拟)已知等比数列{an}的前n项和Sn=λ-2n+1,则λ=( )
A.-1 B.1
C.-2 D.2
√
D [当n≥2时,an=Sn-Sn-1==-2n,
又∵a1=S1=λ-4,数列{an}是等比数列,
∴=,即=,解得λ=2.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2025·齐齐哈尔市建华区模拟)在正项等比数列{an}中,已知a3=8,a5=2,其前n项和为Sn,则下列说法中正确的是( )
A.a1=32 B.an=26-n
C.=4 D.S6=63
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [设公比为q(q>0),因为a3=8,a5=2,所以q2==,
即q=,a1==32,A正确;
an=a1qn-1=32·=26-n,故B正确;
=q2=,故C错误;S6==63,故D正确.故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·厦门调研)等比数列{an}满足an>0,且a2a8=4,则log2a1+log2a2+log2a3+…+log2a9=________.
9 [由题意可得a2a8==4,a5>0,所以a5=2,则原式=log2(a1a2…a9)=9log2a5=9.]
9
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·北京模拟)设等比数列{an}满足a1+a2=48,a4+a5=6,则公比q=________,log2(a1a2a3…an)的最大值为________.
15 [因为a1+a2=48,所以由a4+a5=6,
可得q3(a1+a2)=6,q3=,q=.
由a1+a2=48,可得a1+a1=48,解得a1=32,
15
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以an=32·=26-n,
log2(a1a2a3…an)=log2(25·24·…·26-n)=log2=,
因为=-+,n∈N*,
所以当n=5或n=6时,有最大值,最大值为15.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·射洪市三模)等比数列{an}中,a1=1,a7=4a5.
(1)求{an}的通项公式;
(2)记Sn为{an}的前n项和,若Sm=31,求m的值.
[解] (1)∵等比数列{an}中,a1=1,a7=4a5,
∴1×q6=4×(1×q4),∴q2=4,解得q=±2,
当q=2时,an=2n-1,
当q=-2时,an=(-2)n-1,
∴{an}的通项公式为an=2n-1或an=(-2)n-1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)当a1=1,q=-2时,Sn===,
由Sm=31,得=31,m∈N*,无解;
当a1=1,q=2时,Sn===2n-1,
由Sm=31,得2m-1=31,m∈N*,
解得m=5.
综上,m的值为5.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2025·海淀区模拟)已知数列{an}满足a1=,且an+1=(n∈N*).
(1)求证:数列是等比数列,并求出{an}的通项公式;
(2)若+…+<2 025,求满足条件的最大整数n.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)证明:在数列{an}中,a1=,an+1=(n∈N*),
所以=,
所以-1==,且-1=,
所以数列是首项为,公比为的等比数列,
所以-1==1+,{an}的通项公式为an=.
(2)若+…+<2 025,
则n++…+=n+=n+1-<2 025,
所以n<2 024+,n∈N*,所以满足条件的最大整数n为2 024.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
第六章 数列
第3课时 等比数列
[考试要求] 1.理解等比数列的概念.
2.掌握等比数列的通项公式与前n项和公式.
3.了解等比数列与指数函数的关系.
考点一 等比数列基本量的运算
1.通项公式:an=____________=amqn-m.
2.前n项和公式:Sn=
提醒:(1)求等比数列前n项和时,若公比q不明确,需分类讨论.
(2)当q≠1时,等比数列{an}的前n项和Sn=A+B·Cn A+B=0,公比q=C(A,B,C均不为零).
a1qn-1
na1(q=1)
(q≠1)
[典例1] (1)(2024·盐城一模)等比数列{an}的前n项和为Sn,已知S3=a2+5a1,a5=4,则a1=( )
A. B.-
C. D.-
(2)记Sn为等比数列{an}的前n项和.若a5-a3=12,a6-a4=24,则等于( )
A.2n-1 B.2-21-n
C.2-2n-1 D.21-n-1
√
√
(1)A (2)B [(1)设公比为q,S3=a2+5a1,所以a3=4a1=a1q2,
所以q2=4,又a5=a1q4=16a1=4,
所以a1=.故选A.
(2)法一:设等比数列{an}的公比为q,易知q≠1,
则由题可得解得
所以Sn==2n-1,
an=a1qn-1=2n-1,所以==2-21-n.
法二:设等比数列{an}的公比为q,易知q≠1,
因为====2,
所以q=2,所以===2-21-n.]
反思领悟 (1)等比数列的通项公式an=a1qn-1与前n项和公式Sn==(q≠1)中共涉及五个量a1,an,q,n,Sn.已知其中三个就能求另外两个(简称“知三求二”).
(2)等比数列的前n项和公式涉及对公比q的分类讨论,当q=1时,{an}的前n项和Sn=na1;当q≠1时,{an}的前n项和Sn==.
巩固迁移1 (1)(2025·徐州模拟)已知数列{an}为等比数列,a2=6,6a1+a3=30,则a4=________.
(2)(2023·全国甲卷)记Sn为等比数列{an}的前n项和.若8S6=7S3,则{an}的公比为________.
(1)54或24 (2)- [(1)由
解得或
a4=a1·q3=2×33=54或a4=3×23=24.
54或24
-
(2)若q=1,则由8S6=7S3得8×6a1=7×3a1,则a1=0,不合题意,所以q≠1.
当q≠1时,因为8S6=7S3,
所以=,
即8(1-q6)=7(1-q3),
即8(1+q3)(1-q3)=7(1-q3),即8(1+q3)=7,
解得q=-.]
考点二 等比数列的判定与证明
1.等比数列的定义:一般地,如果一个数列从第__项起,每一项与它的前一项的比都等于__________(不为零),那么这个数列叫做等比数列.这个常数叫做等比数列的____,通常用字母q表示,定义的表达式为=q(n∈N*,q为非零常数).
2.等比中项:如果在a与b中间插入一个数G,使a,G,b成等比数列,那么____叫做a与b的等比中项,此时,G2=ab.
提醒:“G2=ab”是“a,G,b成等比数列”的必要不充分条件.
2
同一个常数
公比
G
[典例2] (2025·八省联考节选)已知数列{an}中,a1=3,an+1=.
(1)证明:数列为等比数列;
(2)求{an}的通项公式.
[解] (1)证明:因为an+1=,a1=3>0,
所以an>0,所以==,
所以1-==.
因为1-=≠0,
所以数列是以为首项,为公比的等比数列.
(2)由(1)知,1-==,
所以=1-,所以an==.
反思领悟 通常用定义法证明一个数列为等比数列.即=q(q≠0).本例只需证明=≠0.
巩固迁移2 已知数列{an}中,a1=2,且an=2an-1-n+2(n≥2,n∈N*).
(1)求a2,a3,并证明{an-n}是等比数列;
(2)求通项公式an.
[解] (1)由a1=2,an=2an-1-n+2(n≥2,n∈N*),
得a2=2a1-2+2=4,a3=2a2-3+2=7,
∵an-n=2an-1-2n+2=2[an-1-(n-1)],
∴=2(n≥2,n∈N*),
又∵a1-1=1,
∴{an-n}是首项为1,公比为2的等比数列.
(2)由(1)知an-n=1×2n-1,
∴an=2n-1+n.
考点三 等比数列的性质
1.等比数列的常用性质
(1)若m+n=p+q,则__________________,其中m,n,p,q∈N*.特别地,若2w=m+n,则__________,其中m,n,w∈N*.
(2)ak,ak+m,ak+2m,…仍是等比数列,公比为____(k,m∈N*).
(3)若数列{an},{bn}是两个项数相同的等比数列,则数列{ban},{pan·qbn}和也是等比数列(b,p,q≠0).
am·an=ap·aq
=am·an
qm
(4)若或则等比数列{an}递____.
若或则等比数列{an}递____.
增
减
2.等比数列前n项和的常用性质
若等比数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn,q=-1且n为偶数时除外.
提醒:(1)由an+1=qan,q≠0,并不能断定{an}为等比数列,还要验证a1≠0.
(2)等比数列的前n项和Sn==qn,令A=-,可以写成Sn=Aqn-A(其中A≠0,q≠1).
[常用结论]
1.数列{an}是等比数列.
(1)若a1·a2·…·an=Tn,则Tn,,…成等比数列.
(2)若Sn是其前n项和,数列{an}的项数为2n,则=q;若项数为2n+1,则=q或=q.
2.三个数成等比数列,通常设为,x,xq;四个符号相同的数成等比数列,通常设为,xq,xq3.
考向1 项的性质
[典例3] 已知数列{an}是等比数列,若a2,a48是方程2x2-7x+6=0的两个根,则a1·a2·a25·a48·a49的值为( )
A. B.9
C.±9 D.243
√
C [若a2,a48是2x2-7x+6=0的两个根,
则a2+a48=,a2·a48==3,
因为数列{an}是等比数列,a2·a48==3,
所以a25=±,a1·a2·a25·a48·a49==±9.故选C.]
反思领悟 在等比数列中,两项之积可转化为另外两项之积或某项的平方,通过本例要树立这一“转化意识”.
巩固迁移3 (2023·全国乙卷)已知{an}为等比数列,a2a4a5=a3a6,a9a10=-8,则a7=________.
-2 [法一:设数列{an}的公比为q,则由a2a4a5=a3a6,得a1q·a1q3·a1q4=a1q2·a1q5.又因为a1≠0,且q≠0,所以可得a1q=1.①
又因为a9a10=a1q8·a1q9=q17=-8,②
所以由①②可得q15=-8,q5=-2,所以a7=a1q6=a1q·q5=-2.
-2
法二:设数列{an}的公比为q.因为a4a5=a3a6≠0,所以a2=1.
又因为a9a10=a2q7·a2q8=q15=-8,于是q5=-2,所以a7=a2q5=-2.]
考向2 和的性质
[典例4] (2023·新高考Ⅱ卷)记Sn为等比数列{an}的前n项和,若S4=-5,S6=21S2,则S8=( )
A.120 B.85
C.-85 D.-120
√
C [法一:设等比数列{an}的公比为q(q≠0),由题意易知q≠1,则
化简整理得
所以S8==×(1-44)=-85.故选C.
法二:易知S2,S4-S2,S6-S4,S8-S6,…为等比数列,所以(S4-S2)2=S2·(S6-S4),解得S2=-1或S2=.当S2=-1时,由(S6-S4)2=(S4-S2)·(S8-S6),解得S8=-85;当S2=时,结合S4=-5得
化简可得q2=-5,不成立,舍去.
所以S8=-85.故选C.]
反思领悟 本例方法一关键是把和q2都“整体看待”,减少了运算量.方法二利用在等比数列中,S2,S4-S2,S6-S4,S8-S6,…仍为等比数列,但求出S2后,要注意检验.
巩固迁移4 (1)(2025·山西大同模拟)已知等比数列{an}共有2n项,其和为-240,且奇数项的和比偶数项的和大80,则公比q=________.
(2)(人教A版选择性必修第二册P37例9改编)设等比数列{an}的前n项和为Sn,若=3,则=________.
2
(1)2 (2) [(1)由题意,得
解得所以q===2.
(2)设等比数列{an}的公比为q,易知q≠-1,由等比数列前n项和的性质可知S3,S6-S3,S9-S6仍成等比数列,
∴=,又由已知得S6=3S3,
∴S9-S6=4S3,∴S9=7S3,∴=.]
随堂练习
√
1.(2025·周口市川汇区模拟)在等比数列{an}中,a1,a8是方程3x2+2x-6=0的两个根,则a4·a5=( )
A.-6 B.-2
C.- D.2
B [∵在等比数列{an}中,a1,a8是方程3x2+2x-6=0的两个根,
∴a4a5=a1a8=-=-2.故选B.]
2.(多选)(2025·太原模拟)设等比数列{an}的公比为q,则下列结论正确的是( )
A.数列{anan+1}是公比为q2的等比数列
B.数列{an+an+1}是公比为q的等比数列
C.数列{an-an+1}是公比为q的等比数列
D.数列是公比为的等比数列
√
√
AD [对于A,由=q2(n≥2)知数列{anan+1}是公比为q2的等比数列;对于B,当q=-1时,数列{an+an+1}的项中有0,不是等比数列;对于C,当q=1时,数列{an-an+1}的项中有0,不是等比数列;对于D,==,所以数列是公比为的等比数列.故选AD.]
3.(2024·东北三校联考)已知数列{an}为等比数列,其前n项和为Sn,若a2a6=-2a7,S3=-6,则a6等于( )
A.-2或32 B.-2或64
C.2或-32 D.2或-64
√
B [数列{an}为等比数列,
a2a6=-2a7=a1a7,解得a1=-2,
设数列{an}的公比为q,则S3=-6=-2-2q-2q2,
解得q=-2或q=1,
当q=-2时,a6=(-2)6=64,
当q=1时,a6=-2.故选B.]
4.在等比数列{an}中,已知a1a3=36,a2+a4=60,则a1+q=________.
±5 [设等比数列{an}的首项为a1,公比为q,由等比数列的性质得a1a3==36,又因为a2+a4=a2(1+q2)=60,所以a2>0,a2=6,所以1+q2=10,解得q=±3.当q=3时,由a2=a1q=6,可得a1=2;当q=-3时,由a2=a1q=6,可得a1=-2,
所以或则a1+q=±5.]
±5
【教用·备选题】
1.(2025·中山市模拟)数列{an}满足an+1=,a1=,若an=,则项数n为( )
A.3 B.4
C.5 D.6
√
C [因为数列{an}满足an+1=an,a1=,
所以数列{an}是以为首项,为公比的等比数列,若an==,
则项数n=5.
故选C.]
2.(2025·衡阳模拟)已知{an}是等比数列,且a6-a4=-24,a7-a5=48,则a1=( )
A.-1 B.
C.1 D.2
√
C [因为{an}是等比数列,且a6-a4=a4(q2-1)=-24,a7-a5=a5(q2-1)=48,
两式相除可得,=q=-2,
所以a6-a4=a1(q5-q3)=-24a1=-24,
所以a1=1.
故选C.]
3.(2025·贵阳模拟)设等比数列{an}的前n项和为Sn,a2+a4=5,a3+a5=10,则S6=( )
A. B.63
C. D.31
√
A [设等比数列{an}的公比为q,∵a2+a4=5,a3+a5=10,
∴q(a2+a4)=5q=10,a1q2(1+q2)=10,
联立解得a1=,q=2,则S6==.
故选A.]
4.(多选)(2025·南阳模拟)若数列{an}是等比数列,且an>0(n∈N*),则下列结论正确的是( )
A.数列}是等比数列
B.数列{an+1-an}是等比数列
C.数列{a2n}是等比数列
D.数列{lg an}是等比数列
√
√
AC [设等比数列{an}的公比为q,因为an>0(n∈N*),所以q>0,
对于==q2,所以数列是等比数列,故A正确;
对于B,当q=1时,等比数列{an}为正项常数列,此时an+1-an=0,所以数列{an+1-an}不是等比数列,故B错误;
对于C,==q2,所以数列{a2n}是等比数列,故C正确;
对于D,若an=1,则lg an=0,所以数列{lg an}不是等比数列,故D错误.
故选AC.]
5.(2025·辽宁模拟)已知等比数列{an}的前n项和为Sn,a1=,8S6=7S3,若λ≥Sn恒成立,则λ的最小值为( )
A. B.
C. D.1
√
C [设等比数列{an}的公比为q,由8S6=7S3,得8(S6-S3)=-S3,
则a4+a5+a6=-(a1+a2+a3),即q3(a1+a2+a3)=-(a1+a2+a3),因为an≠0,所以q3=-,解得q=-,又因为a1=,所以an=,所以Sn==,
当n为奇数时,Sn=,所以Sn≤S1=,
当n为偶数时,Sn=<,所以(Sn)max=,所以λ≥.
故选C.]
6.(2025·黄山模拟)等比数列{an}的前n项和为Sn,前n项积为Tn,a4-a2=6,a5-a3=12,当最小时,n的值为( )
A.3 B.4
C.5 D.6
√
C [因为{an}是等比数列,所以=q==2,
又因为a4-a2=6=a2(q2-1)=3a2,a2=2,
所以a1=1,an=2n-1,
Tn=20×21×22×…×2n-1=20+1+2+…+(n-1)=,
Sn==2n-1,==,
因为y=2t在R上单调递增,t=的图象开口向上,当n=5时取最小值,所以当n=5时, 取最小值.
故选C.]
7.(多选)(2025·长沙模拟)设等比数列{an}的公比为q,前n项积为Tn,下列说法正确的是( )
A.若T8=T12,则a10a11=1
B.若T8=T12,则T20=1
C.若a1=1 024,且T10为数列{Tn}的唯一最大项,则
√
√
√
BCD [对于A,若T8=T12,则有=a9a10a11·a12=1,
结合a9a12=a10a11,可得a10a11=±1,故A不正确;
对于B,若T8=T12,则有=a9a10a11a12=1,
可知T20=a1a2a3a4…a17a18a19a20=(a9a10a11·a12)5=1,B正确;
对于C,若a1=1 024,且T10为数列{Tn}的唯一最大项,
则公比q>0,a10>1且a11<1,即解得
则q>0,<1且>1,即a11<1,a10a11>1,可知0<q<1,
由此得到T20=(a10a11)10>1,T21=<1,当n≥21时,Tn均小于1.
综上所述,使得Tn>1成立的n的最大值为20,故D正确.故选BCD.]
8.已知正项等比数列{an}的前n项和为Sn,且S8-2S4=5,则a9+a10+a11+a12的最小值为( )
A.10 B.15
C.20 D.25
√
C [由题意可得a9+a10+a11+a12=S12-S8,
由S8-2S4=5,可得S8-S4=S4+5.
又由等比数列的性质知S4,S8-S4,S12-S8成等比数列,
则S4(S12-S8)=(S8-S4)2.
于是a9+a10+a11+a12=S12-S8==S4++10≥2+10=20,
当且仅当S4=5时等号成立.
所以a9+a10+a11+a12的最小值为20.故选C.]
9.(2025·韩城市模拟)已知等比数列{an}的前n项和为Sn,公比q>1,若a2=8,S3=28.
(1)求{an}的通项公式;
(2)证明:>Sn+7.
[解] (1)等比数列{an}中,由于a2=8,S3=28,
则有
解得或(舍去),所以an=a1qn-1=2n+1.
(2)证明:因为Sn==2×2n+1-4,且n∈N*,
所以-Sn-7=(2n+1)2-2×2n+1-3=(2n+1-3)(2n+1+1)>0,
所以>Sn+7.
课后习题(三十九) 等比数列
1.(湘教版选择性必修第一册P26例1改编)在等比数列{an}中,a3=2,a7=8,则a5等于( )
A.5 B.±5 C.4 D.±4
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [∵=a3a7=2×8=16,∴a5=±4.
又∵a5=a3q2>0,∴a5=4.故选C.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版选择性必修第二册P37练习T1(3)改编)在等比数列{an}中,a3=,S3=,则a2的值为( )
A. B.-3
C.- D.-3或
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由S3=a1+a2+a3=a3(q-2+q-1+1),得
q-2+q-1+1=3,即2q2-q-1=0,
解得q=1或q=-.
∴a2==或-3.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教A版选择性必修第二册P34练习T3改编)朱载堉是中国明代一位杰出的音乐家、律学家和历学家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度十三个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为f1,第七个音的频率为f2,则=( )
A.4 B.
C. D.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [依题意,十三个音的频率依次成等比数列,记为{an},设公比为q,则a13=a1q12,又∵a13=2a1,
∴q=,∴==q4=()4=.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第二册P41习题4.3T7(1)改编)已知正项数列{an}的前n项积为Tn,且满足an=(n∈N*).求证:数列为等比数列.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[证明] ∵an=,且an=(n≥2),
∴=(n≥2),∵an>0,∴Tn>0,∴3Tn-1=Tn-1(n≥2),
则Tn-=(n≥2),
当n=1时,a1=T1=,得T1=,
∴T1-=,∴数列是首项为,公比为的等比数列.
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·秦皇岛三模)已知等比数列{an}的前n项和为Sn,满足a4+a5+a6=351,S6=364,则数列{an}的公比为( )
A. B.2
C.3 D.4
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [设等比数列{an}的公比为q(q≠0),
∵a1+a2+a3=S6-(a4+a5+a6)=364-351=13,
∴==27=q3,∴q=3.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·吕梁期末)已知正项等比数列{an}满足a4=16,a6=64,则S5=( )
A.62 B.30或10
C.62或-22 D.30
√
A [设正项等比数列{an}的公比为q(q>0),
则q2===4,解得q=2(负值舍去),
故a1==2,则S5==62.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2025·烟台模拟)已知等比数列{an}的前n项和Sn=λ-2n+1,则λ=( )
A.-1 B.1
C.-2 D.2
√
D [当n≥2时,an=Sn-Sn-1==-2n,
又∵a1=S1=λ-4,数列{an}是等比数列,
∴=,即=,解得λ=2.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2025·齐齐哈尔市建华区模拟)在正项等比数列{an}中,已知a3=8,a5=2,其前n项和为Sn,则下列说法中正确的是( )
A.a1=32 B.an=26-n
C.=4 D.S6=63
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [设公比为q(q>0),因为a3=8,a5=2,所以q2==,
即q=,a1==32,A正确;
an=a1qn-1=32·=26-n,故B正确;
=q2=,故C错误;S6==63,故D正确.故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·厦门调研)等比数列{an}满足an>0,且a2a8=4,则log2a1+log2a2+log2a3+…+log2a9=________.
9 [由题意可得a2a8==4,a5>0,所以a5=2,则原式=log2(a1a2…a9)=9log2a5=9.]
9
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·北京模拟)设等比数列{an}满足a1+a2=48,a4+a5=6,则公比q=________,log2(a1a2a3…an)的最大值为________.
15 [因为a1+a2=48,所以由a4+a5=6,
可得q3(a1+a2)=6,q3=,q=.
由a1+a2=48,可得a1+a1=48,解得a1=32,
15
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以an=32·=26-n,
log2(a1a2a3…an)=log2(25·24·…·26-n)=log2=,
因为=-+,n∈N*,
所以当n=5或n=6时,有最大值,最大值为15.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·射洪市三模)等比数列{an}中,a1=1,a7=4a5.
(1)求{an}的通项公式;
(2)记Sn为{an}的前n项和,若Sm=31,求m的值.
[解] (1)∵等比数列{an}中,a1=1,a7=4a5,
∴1×q6=4×(1×q4),∴q2=4,解得q=±2,
当q=2时,an=2n-1,
当q=-2时,an=(-2)n-1,
∴{an}的通项公式为an=2n-1或an=(-2)n-1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)当a1=1,q=-2时,Sn===,
由Sm=31,得=31,m∈N*,无解;
当a1=1,q=2时,Sn===2n-1,
由Sm=31,得2m-1=31,m∈N*,
解得m=5.
综上,m的值为5.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2025·海淀区模拟)已知数列{an}满足a1=,且an+1=(n∈N*).
(1)求证:数列是等比数列,并求出{an}的通项公式;
(2)若+…+<2 025,求满足条件的最大整数n.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)证明:在数列{an}中,a1=,an+1=(n∈N*),
所以=,
所以-1==,且-1=,
所以数列是首项为,公比为的等比数列,
所以-1==1+,{an}的通项公式为an=.
(2)若+…+<2 025,
则n++…+=n+=n+1-<2 025,
所以n<2 024+,n∈N*,所以满足条件的最大整数n为2 024.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
同课章节目录
