《高考快车道》2026版高三一轮总复习数学(基础版)62 第六章 思维进阶7 传统文化中的数列建模与创新应用 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)62 第六章 思维进阶7 传统文化中的数列建模与创新应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-12-04 00:00:00 | ||
图片预览










文档简介
(共39张PPT)
第六章 数列
思维进阶7 传统文化中的数列建模与创新应用
纵观新高考五年的真题,特别是2024年新高考Ⅰ卷、Ⅱ卷,我们不难发现新一轮高考改革突出了对数列创新应用的考查,所以日常备考要始终贯穿观察、分析、归纳、递推、概括、猜想、应用等能力的培养.
题型一 传统文化中的数列建模
传统文化在数列中一般作为背景考查,发挥育人功能.在解答过程中,要抓住其中特征灵活运用数列知识分析、解决问题.
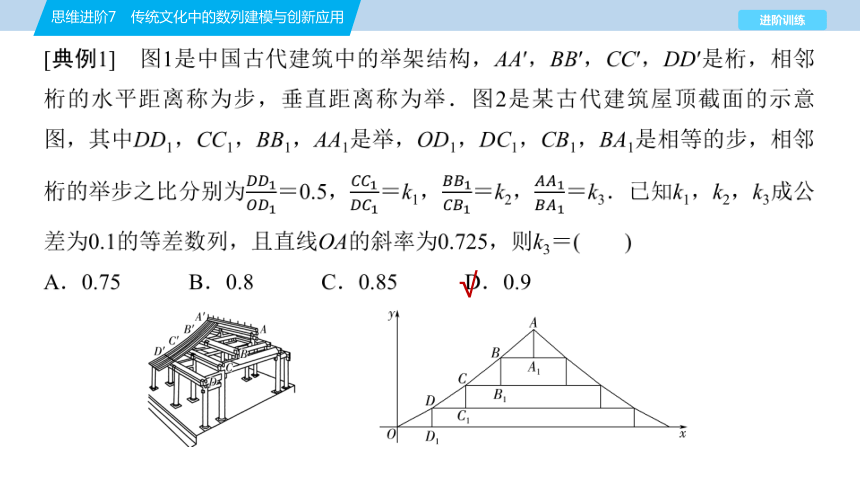
[典例1] 图1是中国古代建筑中的举架结构,AA′,BB′,CC′,DD′是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图,其中DD1,CC1,BB1,AA1是举,OD1,DC1,CB1,BA1是相等的步,相邻桁的举步之比分别为=0.5,=k1,=k2,=k3.已知k1,k2,k3成公差为0.1的等差数列,且直线OA的斜率为0.725,则k3=( )
A.0.75 B.0.8 C.0.85 D.0.9
√
[阅读与思考] 如图,连接OA,延长AA1与x轴交于点A2,则OA2=4OD1.因为k1,k2,k3成公差为0.1的等差数列,所以k1=k3-0.2,k2=k3-0.1,所以CC1=DC1(k3-0.2),BB1=CB1(k3-0.1),AA1=k3BA1,即CC1=OD1(k3-0.2),BB1=OD1(k3-0.1),AA1=k3OD1.又=0.5,所以DD1=,所以AA2=0.5OD1+OD1(k3-0.2)+OD1(k3-0.1)+k3OD1=OD1(3k3+0.2),所以===0.725,解得k3=0.9.故选D.
反思领悟 本例以中国古代建筑中的举架结构为背景,综合应用等差数列、三角函数、解析几何等知识解答.
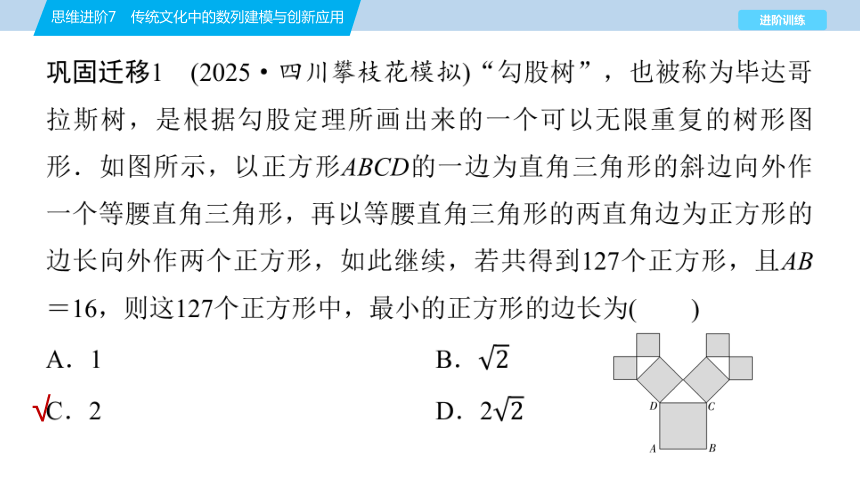
巩固迁移1 (2025·四川攀枝花模拟)“勾股树”,也被称为毕达哥拉斯树,是根据勾股定理所画出来的一个可以无限重复的树形图形.如图所示,以正方形ABCD的一边为直角三角形的斜边向外作一个等腰直角三角形,再以等腰直角三角形的两直角边为正方形的边长向外作两个正方形,如此继续,若共得到127个正方形,且AB=16,则这127个正方形中,最小的正方形的边长为( )
A.1 B.
C.2 D.2
√
C [依题意,不同边长的正方形的个数构成以1为首项,2为公比的等比数列,所以1+2+22+…+2n-1=127,即=127,解得n=7,即有7种边长不同的正方形.又正方形的边长构成以16为首项,为公比的等比数列.因此,最小的正方形的边长为16×=2.故选C.]
题型二 新情境、新定义中的数列问题
对于新信息情境下的数列问题,在读懂题意的前提下,依据题目提供的信息,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使问题得以解决.
[典例2] (2024·烟台二模)欧拉函数φ(n)(n∈N*)的函数值等于所有不超过正整数n,且与n互质的正整数的个数,例如φ(4)=2.已知bn=,n∈N*,Tn是数列{bn}的前n项和,若Tn<M恒成立,则M的最小值为( )
A. B.1
C. D.2
√
[阅读与思考] 因为3为质数,在不超过3n的正整数中,所有能被3整除的正整数的个数为3n-1,
φ(3n)=3n-3n-1=2×3n-1(n∈N*),
所以φ(3n+1)=3n+1-3n=2×3n(n∈N*),
则bn===,
所以Tn=b1+b2+b3+…+bn-1+bn=+…+,
Tn=+…+,
两式相减,可得Tn=+…+=
==,
所以Tn=<,
因为bn=>0,所以Tn在n∈N*上递增,
所以Tn所以M的最小值为.故选A.
反思领悟 本例关键是由欧拉函数定义求出bn=,进而由错位相减法求出Tn,即可求出M的最小值.
巩固迁移2 (2024·上饶市广丰区期末)记[x]表示不超过x的最大整数,〈x〉=x-[x],如[2.4]=2,〈2.4〉=0.4.已知数列{an}的通项公式为an=n-2,数列{bn}满足bn=2[an]-3〈an〉,则b1+b2+b3+…+b20=( )
A.23 B.22
C.24 D.25
√
D [由〈an〉=an-[an],可知bn=2[an]-3〈an〉=5[an]-3an,
记数列{an}和{[an]}的前n项和分别为Sn和Tn,
由an=n-2,得S20=×20×=30,
而[a3n]=[n-2]=n-2,[a3n+1]==n-2,[a3n+2]==n-2,n∈N*,
T20=[a1]+[a2]+([a3]+[a4]+[a5])+…+([a18]+[a19]+[a20])
=-2-2+3×(-1+0+1+2+3+4)=-4+3×9=23,
则b1+b2+b3+…+b20=5×23-3×30=25.
故选D.]
【教用·备选题】
1.(2024·碑林区月考)如图,将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N*)个点,相应的图案中总的点数记为an,则a2+a3+a4+…+an等于( )
A. B. C. D.
√
C [∵a2=3,a3=6,a4=9,a5=12,∴a2+a3+a4+…+an=3+6+9+12+…+3(n-1)
=(3+3n-3)=.故选C.]
2.(多选)若数列{an}满足a1=a2=1,an=an-1+an-2(n≥3,n∈N*),则称该数列为斐波那契数列.如图所示的“黄金螺旋线”是根据斐波那契数列画出来的曲线.图中的长方形由以斐波那契数为边长的正方形拼接而成,在每个正方形中作圆心角为90°的扇形,连接起来的曲线就是“黄金螺旋线”.记以an为边长的正方形中的扇形面积为bn,数列{bn}的前n项和为Sn.下列结论正确的是( )
A.a9=34
B.a2 024是奇数
C.a2+a4+a6+…+a2 024=a2 025
D.=
√
√
√
ABD [数列{an}为1,1,2,3,5,8,13,21,34,…,所以a9=34,A正确;
由斐波那契数列得每三个数中,前两个为奇数后一个为偶数,
且2 024=3×674+2,所以a2 024是奇数,B正确;
由an-1=an-an-2,得a2=a3-a1,a4=a5-a3,…,
a2 024=a2 025-a2 023,
累加得a2+a4+…+a2 024=a2 025-a1,C错误;
由an=an-1+an-2(n≥3),
得======…=a2 023a2 024,
所以S2 023=
=a2 023a2 024,
所以=,D正确.故选ABD.]
进阶训练(七) 传统文化中的数列建模与创新应用
1.(2024·北京人大附中月考)明代数学家程大位在《算法统宗》中已经给出由n,Sn和d求各项的问题,如九儿问甲歌:“一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七.借问长儿多少岁,各儿岁数要详推.”则该问题中老人的长子的岁数为
( )
A.35 B.32
C.29 D.26
√
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
A [根据题意,九个儿子的岁数从大到小构成公差为-3的等差数列,设长子的岁数为a1,则207=9a1+×(-3),解得a1=35.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
2.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第3项起,每个数等于它前面两个数的和,即an+2=an+1+an(n∈N*),后来人们把这样的一列数组成的数列{an}称为“斐波那契数列”.记a2 022=t,则a1+a3+a5+…+a2 021=( )
A.t2 B.t-1
C.t D.t+1
题号
1
3
5
2
4
6
8
7
9
C [由an+2=an+1+an(n∈N*),得a2 022=a2 021+a2 020=a2 021+a2 019+a2 018=…=a2 021+a2 019+…+a3+a2=a2 021+a2 019+…+a3+a1=t.故选C.]
题号
1
3
5
2
4
6
8
7
9
3.(2024·平顶山联考)《周髀算经》记载:一年有二十四个节气,每个节气晷 (guǐ)长损益相同,夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降、立冬、小雪、大雪是连续十二个节气,其日影子长依次成等差数列.经记录测算,夏至、处暑、霜降三个节气日影子长之和为16.5尺,这十二节气的所有日影子长之和为84尺,则夏至的日影子长为( )
A.1尺 B.1.25尺
C.1.5尺 D.2尺
√
题号
1
3
5
2
4
6
8
7
9
C [由题意可知,十二个节气的日影子长为等差数列,设为a1,a2,…,a12,公差为d,其前n项和为Sn,则
即
解得a1=1.5.故选C.]
题号
1
3
5
2
4
6
8
7
9
4.(2024·湖南永州联考)“三分损益法”是古代中国发明的制定音律时所用的生律法.例如:假设能发出第一个基准音的乐器的长度为36,那么能发出第二个基准音的乐器的长度为36×=24,能发出第三个基准音的乐器的长度为24×=32,……,也就是依次先减少三分之一,后增加三分之一,以此类推.现有一兴趣小组采用此规律构造了一个共12项的数列{an}用来研究数据的变化,已知a8=192,则a5=( )
A.324 B.297
C.256 D.168
√
题号
1
3
5
2
4
6
8
7
9
A [由损益规律可知a8=a5,
即a5=192,
解得a5=324.故选A.]
题号
1
3
5
2
4
6
8
7
9
5.(2024·武汉市蔡甸区期末)已知Sn是数列{bn}的前n项和,若(1-2x)2 025=a0+a1x+a2x2+…+a2 025x2 025,数列{bn}的首项b1=+…+,bn+1·bn=2n(n∈N*),则S2 025=( )
A.-3-21 014 B.-2-3·21 012
C.2-3·21 012 D.3-21 014
√
题号
1
3
5
2
4
6
8
7
9
D [当x=0时,a0=1,当x=时,a0++…+=0,
所以b1=-a0=-1,又因为b2·b1=2,所以b2=-2,
因为所以=2,
S2 025=b1+b2+b3+…+b2 025=(b1+b3+…+b2 025)+(b2+b4+…+b2 024)
==3-21 014.故选D.]
题号
1
3
5
2
4
6
8
7
9
6.如图1是古筝鸣箱俯视图,鸣箱有多根弦,每根弦下有一只弦码,弦码又叫雁柱,用于调节音高和传振.图2是根据图1绘制的古筝弦及其弦码简易直观图.在直观图中,每根弦都垂直于x轴,左边第一根弦在y轴上,相邻两根弦间的距离为1,弦码所在的曲线(又称为雁柱曲线)方程为y=,第n(n∈N,第0根弦表示与y轴重合的弦)根弦分别与雁柱曲线和直线l:y=x+1交于点An(xn,yn)和Bn(x′n,y′n),则 =( )
参考数据:1.122=8.14.
A.814 B.900
C.914 D.1 000
√
题号
1
3
5
2
4
6
8
7
9
C [根据题意,第n根弦分别与雁柱曲线y=1.1x和直线l:y=x+1交于点An(xn,yn)和Bn(x′n,y′n),
则yn=1.1n,y′n=n+1,则有yny′n=(n+1)1.1n,
设Tn= 则Tn=1+2×1.1+3×1.12+4×1.13+…+21×1.120,①
1.1Tn=1.1+2×1.12+3×1.13+4×1.14+…+21×1.121,②
①-②可得-0.1Tn=+…+1.120-21×1.121==1+10×(1.121-1.1)-21×1.121=
-10-10×1.122=-91.4,
所以Tn=914,故 =914.故选C.]
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
7.(2025·甘肃金昌模拟)我国古代数学著作《九章算术》有如下问题,“今有金箠,长五尺.斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”意思是“现有一根金杖,长五尺,一头粗,一头细.在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上述的已知条件,若金杖由粗到细是均匀变化的,估计此金杖总重量约为________斤.
15 [由题意知每一尺的重量构成等差数列,设首项为2,则第5项为4,所以总重量为×5=15斤.]
15
题号
1
3
5
2
4
6
8
7
9
8.(2025·江西南昌模拟)我国古代的《洛书》中记载着世界上最古老的一个幻方:如图将1,2,3,…,9填入3×3的方格内,使三行、三列和两条对角线上的三个数字之和都等于15. 一般地,将连续的正整数1,2,3,…,n2填入n×n个方格中,使得每行、每列和两条对角线上的数字之和都相等,这个正方形叫做n阶幻方. 记n阶幻方的每列的数字之和为Nn,如图三阶幻方N3=15,那么N5=________.
65
题号
1
3
5
2
4
6
8
7
9
65 [由n阶幻方填入1,2,3,…,n2,共n列,这n2个数字之和为1+2+3+…+n2,由这n列之和都相等,则每一列和Nn===.
故N5==65.]
题号
1
3
5
2
4
6
8
7
9
9.(2025·成都模拟)记Sn(x)=x+x2+x3+…+xn-2(x∈R,n∈N*).
(1)当x=2时,Sn(2)为数列{an}的前n项和,求{an}的通项公式;
(2)记S′2 024(x)是S2 024(x)的导函数,求S′2 024(2).
[解] (1)当n=1时,a1=S1(2)=0,
当n≥2时,an=Sn(2)-Sn-1(2)=(2+22+…+2n-2)-(2+22+…+2n-1-2)=2n,
又∵当n=1时,a1=0不满足上式,∴an=
题号
1
3
5
2
4
6
8
7
9
(2)∵S2 024(x)=x+x2+x3+…+x2 024-2,
∴S′2 024(x)=1+2x+3x2+…+2 024x2 023,
S′2 024(2)=1+2×2+3×22+…+2 024×22 023,①
2S′2 024(2)=2+2×22+3×23+…+2 024×22 024,②
①-②得,-S′2 024(2)=1+2+22+…+22 023-2 024×22 024=-2 024×22 024=-2 023×22 024-1,
∴S′2 024(2)=2 023×22 024+1.
谢 谢 !
第六章 数列
思维进阶7 传统文化中的数列建模与创新应用
纵观新高考五年的真题,特别是2024年新高考Ⅰ卷、Ⅱ卷,我们不难发现新一轮高考改革突出了对数列创新应用的考查,所以日常备考要始终贯穿观察、分析、归纳、递推、概括、猜想、应用等能力的培养.
题型一 传统文化中的数列建模
传统文化在数列中一般作为背景考查,发挥育人功能.在解答过程中,要抓住其中特征灵活运用数列知识分析、解决问题.
[典例1] 图1是中国古代建筑中的举架结构,AA′,BB′,CC′,DD′是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图,其中DD1,CC1,BB1,AA1是举,OD1,DC1,CB1,BA1是相等的步,相邻桁的举步之比分别为=0.5,=k1,=k2,=k3.已知k1,k2,k3成公差为0.1的等差数列,且直线OA的斜率为0.725,则k3=( )
A.0.75 B.0.8 C.0.85 D.0.9
√
[阅读与思考] 如图,连接OA,延长AA1与x轴交于点A2,则OA2=4OD1.因为k1,k2,k3成公差为0.1的等差数列,所以k1=k3-0.2,k2=k3-0.1,所以CC1=DC1(k3-0.2),BB1=CB1(k3-0.1),AA1=k3BA1,即CC1=OD1(k3-0.2),BB1=OD1(k3-0.1),AA1=k3OD1.又=0.5,所以DD1=,所以AA2=0.5OD1+OD1(k3-0.2)+OD1(k3-0.1)+k3OD1=OD1(3k3+0.2),所以===0.725,解得k3=0.9.故选D.
反思领悟 本例以中国古代建筑中的举架结构为背景,综合应用等差数列、三角函数、解析几何等知识解答.
巩固迁移1 (2025·四川攀枝花模拟)“勾股树”,也被称为毕达哥拉斯树,是根据勾股定理所画出来的一个可以无限重复的树形图形.如图所示,以正方形ABCD的一边为直角三角形的斜边向外作一个等腰直角三角形,再以等腰直角三角形的两直角边为正方形的边长向外作两个正方形,如此继续,若共得到127个正方形,且AB=16,则这127个正方形中,最小的正方形的边长为( )
A.1 B.
C.2 D.2
√
C [依题意,不同边长的正方形的个数构成以1为首项,2为公比的等比数列,所以1+2+22+…+2n-1=127,即=127,解得n=7,即有7种边长不同的正方形.又正方形的边长构成以16为首项,为公比的等比数列.因此,最小的正方形的边长为16×=2.故选C.]
题型二 新情境、新定义中的数列问题
对于新信息情境下的数列问题,在读懂题意的前提下,依据题目提供的信息,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使问题得以解决.
[典例2] (2024·烟台二模)欧拉函数φ(n)(n∈N*)的函数值等于所有不超过正整数n,且与n互质的正整数的个数,例如φ(4)=2.已知bn=,n∈N*,Tn是数列{bn}的前n项和,若Tn<M恒成立,则M的最小值为( )
A. B.1
C. D.2
√
[阅读与思考] 因为3为质数,在不超过3n的正整数中,所有能被3整除的正整数的个数为3n-1,
φ(3n)=3n-3n-1=2×3n-1(n∈N*),
所以φ(3n+1)=3n+1-3n=2×3n(n∈N*),
则bn===,
所以Tn=b1+b2+b3+…+bn-1+bn=+…+,
Tn=+…+,
两式相减,可得Tn=+…+=
==,
所以Tn=<,
因为bn=>0,所以Tn在n∈N*上递增,
所以Tn
反思领悟 本例关键是由欧拉函数定义求出bn=,进而由错位相减法求出Tn,即可求出M的最小值.
巩固迁移2 (2024·上饶市广丰区期末)记[x]表示不超过x的最大整数,〈x〉=x-[x],如[2.4]=2,〈2.4〉=0.4.已知数列{an}的通项公式为an=n-2,数列{bn}满足bn=2[an]-3〈an〉,则b1+b2+b3+…+b20=( )
A.23 B.22
C.24 D.25
√
D [由〈an〉=an-[an],可知bn=2[an]-3〈an〉=5[an]-3an,
记数列{an}和{[an]}的前n项和分别为Sn和Tn,
由an=n-2,得S20=×20×=30,
而[a3n]=[n-2]=n-2,[a3n+1]==n-2,[a3n+2]==n-2,n∈N*,
T20=[a1]+[a2]+([a3]+[a4]+[a5])+…+([a18]+[a19]+[a20])
=-2-2+3×(-1+0+1+2+3+4)=-4+3×9=23,
则b1+b2+b3+…+b20=5×23-3×30=25.
故选D.]
【教用·备选题】
1.(2024·碑林区月考)如图,将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N*)个点,相应的图案中总的点数记为an,则a2+a3+a4+…+an等于( )
A. B. C. D.
√
C [∵a2=3,a3=6,a4=9,a5=12,∴a2+a3+a4+…+an=3+6+9+12+…+3(n-1)
=(3+3n-3)=.故选C.]
2.(多选)若数列{an}满足a1=a2=1,an=an-1+an-2(n≥3,n∈N*),则称该数列为斐波那契数列.如图所示的“黄金螺旋线”是根据斐波那契数列画出来的曲线.图中的长方形由以斐波那契数为边长的正方形拼接而成,在每个正方形中作圆心角为90°的扇形,连接起来的曲线就是“黄金螺旋线”.记以an为边长的正方形中的扇形面积为bn,数列{bn}的前n项和为Sn.下列结论正确的是( )
A.a9=34
B.a2 024是奇数
C.a2+a4+a6+…+a2 024=a2 025
D.=
√
√
√
ABD [数列{an}为1,1,2,3,5,8,13,21,34,…,所以a9=34,A正确;
由斐波那契数列得每三个数中,前两个为奇数后一个为偶数,
且2 024=3×674+2,所以a2 024是奇数,B正确;
由an-1=an-an-2,得a2=a3-a1,a4=a5-a3,…,
a2 024=a2 025-a2 023,
累加得a2+a4+…+a2 024=a2 025-a1,C错误;
由an=an-1+an-2(n≥3),
得======…=a2 023a2 024,
所以S2 023=
=a2 023a2 024,
所以=,D正确.故选ABD.]
进阶训练(七) 传统文化中的数列建模与创新应用
1.(2024·北京人大附中月考)明代数学家程大位在《算法统宗》中已经给出由n,Sn和d求各项的问题,如九儿问甲歌:“一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七.借问长儿多少岁,各儿岁数要详推.”则该问题中老人的长子的岁数为
( )
A.35 B.32
C.29 D.26
√
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
A [根据题意,九个儿子的岁数从大到小构成公差为-3的等差数列,设长子的岁数为a1,则207=9a1+×(-3),解得a1=35.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
2.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第3项起,每个数等于它前面两个数的和,即an+2=an+1+an(n∈N*),后来人们把这样的一列数组成的数列{an}称为“斐波那契数列”.记a2 022=t,则a1+a3+a5+…+a2 021=( )
A.t2 B.t-1
C.t D.t+1
题号
1
3
5
2
4
6
8
7
9
C [由an+2=an+1+an(n∈N*),得a2 022=a2 021+a2 020=a2 021+a2 019+a2 018=…=a2 021+a2 019+…+a3+a2=a2 021+a2 019+…+a3+a1=t.故选C.]
题号
1
3
5
2
4
6
8
7
9
3.(2024·平顶山联考)《周髀算经》记载:一年有二十四个节气,每个节气晷 (guǐ)长损益相同,夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降、立冬、小雪、大雪是连续十二个节气,其日影子长依次成等差数列.经记录测算,夏至、处暑、霜降三个节气日影子长之和为16.5尺,这十二节气的所有日影子长之和为84尺,则夏至的日影子长为( )
A.1尺 B.1.25尺
C.1.5尺 D.2尺
√
题号
1
3
5
2
4
6
8
7
9
C [由题意可知,十二个节气的日影子长为等差数列,设为a1,a2,…,a12,公差为d,其前n项和为Sn,则
即
解得a1=1.5.故选C.]
题号
1
3
5
2
4
6
8
7
9
4.(2024·湖南永州联考)“三分损益法”是古代中国发明的制定音律时所用的生律法.例如:假设能发出第一个基准音的乐器的长度为36,那么能发出第二个基准音的乐器的长度为36×=24,能发出第三个基准音的乐器的长度为24×=32,……,也就是依次先减少三分之一,后增加三分之一,以此类推.现有一兴趣小组采用此规律构造了一个共12项的数列{an}用来研究数据的变化,已知a8=192,则a5=( )
A.324 B.297
C.256 D.168
√
题号
1
3
5
2
4
6
8
7
9
A [由损益规律可知a8=a5,
即a5=192,
解得a5=324.故选A.]
题号
1
3
5
2
4
6
8
7
9
5.(2024·武汉市蔡甸区期末)已知Sn是数列{bn}的前n项和,若(1-2x)2 025=a0+a1x+a2x2+…+a2 025x2 025,数列{bn}的首项b1=+…+,bn+1·bn=2n(n∈N*),则S2 025=( )
A.-3-21 014 B.-2-3·21 012
C.2-3·21 012 D.3-21 014
√
题号
1
3
5
2
4
6
8
7
9
D [当x=0时,a0=1,当x=时,a0++…+=0,
所以b1=-a0=-1,又因为b2·b1=2,所以b2=-2,
因为所以=2,
S2 025=b1+b2+b3+…+b2 025=(b1+b3+…+b2 025)+(b2+b4+…+b2 024)
==3-21 014.故选D.]
题号
1
3
5
2
4
6
8
7
9
6.如图1是古筝鸣箱俯视图,鸣箱有多根弦,每根弦下有一只弦码,弦码又叫雁柱,用于调节音高和传振.图2是根据图1绘制的古筝弦及其弦码简易直观图.在直观图中,每根弦都垂直于x轴,左边第一根弦在y轴上,相邻两根弦间的距离为1,弦码所在的曲线(又称为雁柱曲线)方程为y=,第n(n∈N,第0根弦表示与y轴重合的弦)根弦分别与雁柱曲线和直线l:y=x+1交于点An(xn,yn)和Bn(x′n,y′n),则 =( )
参考数据:1.122=8.14.
A.814 B.900
C.914 D.1 000
√
题号
1
3
5
2
4
6
8
7
9
C [根据题意,第n根弦分别与雁柱曲线y=1.1x和直线l:y=x+1交于点An(xn,yn)和Bn(x′n,y′n),
则yn=1.1n,y′n=n+1,则有yny′n=(n+1)1.1n,
设Tn= 则Tn=1+2×1.1+3×1.12+4×1.13+…+21×1.120,①
1.1Tn=1.1+2×1.12+3×1.13+4×1.14+…+21×1.121,②
①-②可得-0.1Tn=+…+1.120-21×1.121==1+10×(1.121-1.1)-21×1.121=
-10-10×1.122=-91.4,
所以Tn=914,故 =914.故选C.]
题号
1
3
5
2
4
6
8
7
9
题号
1
3
5
2
4
6
8
7
9
7.(2025·甘肃金昌模拟)我国古代数学著作《九章算术》有如下问题,“今有金箠,长五尺.斩本一尺,重四斤.斩末一尺,重二斤.问次一尺各重几何?”意思是“现有一根金杖,长五尺,一头粗,一头细.在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上述的已知条件,若金杖由粗到细是均匀变化的,估计此金杖总重量约为________斤.
15 [由题意知每一尺的重量构成等差数列,设首项为2,则第5项为4,所以总重量为×5=15斤.]
15
题号
1
3
5
2
4
6
8
7
9
8.(2025·江西南昌模拟)我国古代的《洛书》中记载着世界上最古老的一个幻方:如图将1,2,3,…,9填入3×3的方格内,使三行、三列和两条对角线上的三个数字之和都等于15. 一般地,将连续的正整数1,2,3,…,n2填入n×n个方格中,使得每行、每列和两条对角线上的数字之和都相等,这个正方形叫做n阶幻方. 记n阶幻方的每列的数字之和为Nn,如图三阶幻方N3=15,那么N5=________.
65
题号
1
3
5
2
4
6
8
7
9
65 [由n阶幻方填入1,2,3,…,n2,共n列,这n2个数字之和为1+2+3+…+n2,由这n列之和都相等,则每一列和Nn===.
故N5==65.]
题号
1
3
5
2
4
6
8
7
9
9.(2025·成都模拟)记Sn(x)=x+x2+x3+…+xn-2(x∈R,n∈N*).
(1)当x=2时,Sn(2)为数列{an}的前n项和,求{an}的通项公式;
(2)记S′2 024(x)是S2 024(x)的导函数,求S′2 024(2).
[解] (1)当n=1时,a1=S1(2)=0,
当n≥2时,an=Sn(2)-Sn-1(2)=(2+22+…+2n-2)-(2+22+…+2n-1-2)=2n,
又∵当n=1时,a1=0不满足上式,∴an=
题号
1
3
5
2
4
6
8
7
9
(2)∵S2 024(x)=x+x2+x3+…+x2 024-2,
∴S′2 024(x)=1+2x+3x2+…+2 024x2 023,
S′2 024(2)=1+2×2+3×22+…+2 024×22 023,①
2S′2 024(2)=2+2×22+3×23+…+2 024×22 024,②
①-②得,-S′2 024(2)=1+2+22+…+22 023-2 024×22 024=-2 024×22 024=-2 023×22 024-1,
∴S′2 024(2)=2 023×22 024+1.
谢 谢 !
同课章节目录
