《高考快车道》2026版高三一轮总复习数学(基础版)66 第六章 滚动测试卷(三) 第一~六章 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)66 第六章 滚动测试卷(三) 第一~六章 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:56 | ||
图片预览











文档简介
(共43张PPT)
第六章 数列
滚动测试卷(三) 第一~六章
单元检测(一)
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={1,3,a2},B={1,a+2},若B A,则a=( )
A.2 B.1
C.-2 D.-1
A [因为B A,所以a+2=3或a+2=a2.
由a+2=3,得a=1(舍去).
由a+2=a2,得a=-1(舍去)或a=2.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
2.已知复数z满足|z-3+4i|=1,则z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D [由|z-3+4i|=1及复数的几何意义,可得复数z在复平面内对应的点Z(a,b)的轨迹是以(3,-4)为圆心、1为半径的圆,该圆的方程为(a-3)2+(b+4)2=1,所以z在复平面内对应的点位于第四象限.故选D.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
3.记Sn为等比数列{an}的前n项和,若a3a5=2a2a4,则=( )
A.5 B.4
C.3 D.2
C [法一:设等比数列{an}的公比为q,由a3a5=2a2a4,得a1q2·a1q4=2a1q·a1q3,又a1≠0,q≠0,所以q2=2,所以==1+q2=3.故选C.
法二:设等比数列{an}的公比为q,由a3a5=2a2a4,
得a3a5=2a2a4=,
因为a3≠0,所以a5=2a3,
所以q2=2,所以==1+=1+=1+q2=3.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
4.已知平面向量a,b,c满足a+b+c=0,|a|=|b|=1,|c|=,则a与b的夹角为( )
A. B.
C. D.
B [由题意得(a+b)2=2+2a·b=2+2|a||b|·cos 〈a,b〉=2+2cos 〈a,b〉=3,所以cos 〈a,b〉=.
又〈a,b〉∈[0,π],所以〈a,b〉=.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
5.(2025·湖北武汉模拟)已知数列满足a1=-,an+1=1-,则a6=( )
A.- B. C. D.5
B [由题意得a1=-,a2=1-=5,a3=1-=,
a4=1-=-,a5=1-=5,a6=1-=.
故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
6.已知公差为负数的等差数列{an}的前n项和为Sn,若a3,a4,a7是等比数列,则当Sn取最大值时,n=( )
A.2或3 B.2
C.3 D.4
B [设等差数列的公差为d(d<0),则由a3,a4,a7是等比数列,得(a1+3d)2=(a1+2d)(a1+6d),整理得d(2a1+3d)=0,所以2a1+3d=0,即a1=-d,所以Sn=na1+d=n2-2dn=-2d.因为d<0,所以当n=2时,Sn取得最大值-2d.故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
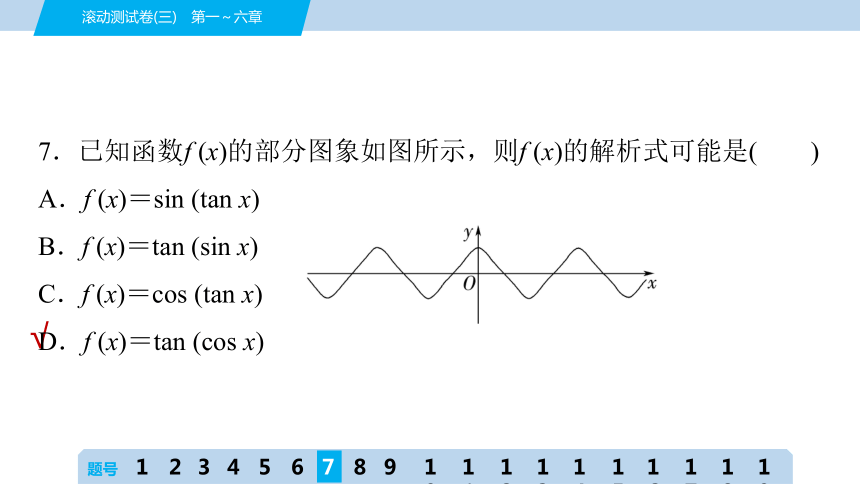
7.已知函数f (x)的部分图象如图所示,则f (x)的解析式可能是( )
A.f (x)=sin (tan x)
B.f (x)=tan (sin x)
C.f (x)=cos (tan x)
D.f (x)=tan (cos x)
D [根据题图可知函数f (x)的图象关于y轴对称,所以函数f (x)为偶函数,且定义域为R.对于A,C,函数f (x)的定义域为,不满足题意,故排除A,C;对于B,f (-x)=tan [sin (-x)]=tan (-sin x)=-tan (sin x)=-f (x),f (x)为奇函数,不满足题意,故排除B.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
8.已知正项数列{an}满足+…+=(n∈N*),若a5-2a6=7,则a1=( )
A. B.1
C. D.2
D [当n=1时,=,即a1a2=3,当n≥2时,由+…+=,得+…+==,以上两式相减,得==,又a1a2=3,所以anan+1=4n2-1(n∈N*),所以a5a6=4×52-1=99,又a5-2a6=7,所以a5=18,a6=.因为a4a5=4×42-1=63,所以a4=.因为a3a4=4×32-1=35,所以a3=10.因为a2a3=4×22-1=15,所以a2=,所以a1=2.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知向量a,b不共线,向量a+b平分a与b的夹角,则下列结论一定正确的是( )
A.a·b=0
B.(a+b)⊥(a-b)
C.向量a与b在a+b上的投影向量相等
D.|a+b|=|a-b|
√
BC [在 ABCD中,令=a,=b,由题意可知, ABCD为菱形,所以||=||,即|a|=|b|,a+b=,a-b=.对于A,因为a·b=|a|·|b|cos 〈a,b〉,所以只有当〈a,b〉=时,才有a·b=0,故A不正确;对于B,由菱形的性质知AC⊥BD,即(a+b)⊥(a-b),故B正确;对于C,因为a2=b2,所以a2+a·b=b2+a·b,即a·(a+b)=b·(a+b),因为a在a+b上的投影向量为·(a+b),b在a+b上的投影向量为·(a+b),所以向量a与b在a+b上的投影向量相等,故C正确;对于D,菱形的对角线不一定相等,故D不正确.综上,故选BC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
10.已知等差数列的前n项和为Sn,正项等比数列的前n项积为Tn,则( )
A.数列是等差数列
B.数列是等比数列
C.数列是等差数列
D.数列是等比数列
√
√
ABD [设的公差为d,的公比为q,
则Sn=n2+n =n+,
所以=是常数,故A正确;
易知==3d是常数,故B正确;
由ln Tn-ln Tn-1=ln bn不是常数,故C错误;
÷==q2是常数,故D正确.
故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
11.已知定义在R上的函数f (x)满足以下条件:①对于任意的x,y∈R,f (x+y)+f (x-y)=2f (x)f (y);②f (0)≠0;③f (k)=0,其中k是正常数.则下列结论正确的是( )
A.f (0)=1
B.f (2k)=1
C.f (x)是偶函数
D.f (x+2k)+f (x)=0
√
√
ACD [f (x+y)+f (x-y)=2f (x)f (y)对任意x,y∈R都成立,
对于A,令x=y=0,得2f (0)=2[f (0)]2,因为f (0)≠0,所以f (0)=1,所以选项A正确;
对于B,令x=y=k,得f (2k)+f (0)=2[f (k)]2,因为f (0)=1,f (k)=0,所以f (2k)=-1,所以选项B错误;
对于C,令x=0,得f (y)+f (-y)=2f (0)f (y),因为f (0)=1,所以f (-y)=
f (y),所以函数f (x)是偶函数,所以选项C正确;
对于D,令y=k,且x+k代换x,得f (x+2k)+f (x)=2f (x+k)f (k),因为
f (k)=0,所以f (x+2k)+f (x)=0,所以选项D正确.综上,故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量a,b,c在网格中的位置如图所示,若网格纸上小正方形的边长为1,则(a-b)·c=________,a·b=________.
2
3
2 3 [建立如图所示的平面直角坐标系,则a=(2,1),b=(2,
-1),c=(0,1),所以a-b=(0,2),a·b=4-1=3,所以(a-b)·c=2.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
13.(2024·盐城调研)写出一个同时满足下列条件①②的等比数列{an}的通项公式an=_________________.
①anan+1<0;②|an|<|an+1|.
(-2)n(答案不唯一)
(-2)n(答案不唯一) [设等比数列{an}的公比为q,
由anan+1<0,可知q<0,
又|an|<|an+1|,所以|q|>1,
所以q<-1,所以q可取-2,
设a1=-2,
则an=-2·(-2)n-1=(-2)n(答案不唯一).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
14.如图为某校数学社团用数学软件制作的“蚊香”.画法如下:在水平直线上取长度为1的线段AB,作一个等边三角形ABC,然后以点B为圆心,AB为半径逆时针画圆弧交线段CB的延长线于点D(第一段圆弧),再以点C为圆心,CD为半径逆时针画圆弧交线段AC的延长线于点E(第二段圆弧),再以点A为圆心,AE为半径逆时针画圆弧……以此类推,当得到的“蚊香”恰好有11段圆弧时,“蚊香”的长度为________.
44π
44π [由题意知每段圆弧所对的圆心角都是,第n段圆弧的半径为n,弧长记为an,
则an=·n,
所以前11段圆弧的长度S11=(1+2+…+11)=44π.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知等差数列{an}的前n项和为Sn,且a4=8,a6=12.
(1)求数列{an}的通项公式;
(2)若Sn=20,求n的值.
[解] (1)∵等差数列{an}的前n项和为Sn,且a4=8,a6=12,
∴解得a1=2,d=2,
∴数列{an}的通项公式an=a1+(n-1)d=2+(n-1)×2=2n.
(2)∵Sn=20,
∴Sn=(a1+an)=(2+2n)=n2+n=20,
解得n=4或n=-5,∵n∈N*,∴n的值为4.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
16.(15分)设数列{an}的前n项和为Sn,an+Sn=1.
(1)求数列{an}的通项公式;
(2)数列{bn}满足anbn=cos ,求{bn}的前50项和T50.
[解] (1)由an+Sn=1,得an-1+Sn-1=1(n≥2),
两式相减得an-an-1+an=0(n≥2),
即an=an-1(n≥2),
当n=1时,2a1=1,得a1=≠0,
所以=(n≥2),故{an}是首项为,公比为的等比数列.
故an=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)由(1)得bn=2n cos ,
所以T50=-22+24-26+28-…-250
=
=-(1+425).
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
17.(15分)在△ABC中,角A,B,C所对的边分别为a,b,c,设向量m=(2sin A,sin A+cos A),n=(cos A,cos A-sin A),f (A)=m·n,A∈.
(1)求函数f (A)的最大值;
(2)若f (A)=0,a=,sin B+sin C=,求△ABC的面积.
[解] 由题知,f (A)=m·n
=(2sin A,sin A+cos A)·(cos A,cos A-sin A)
=2sin A cos A+cos2A-sin2A
=sin2A+cos 2A
=2sin .
因为≤A≤,所以≤2A+,所以-1≤sin ,所以f (A)∈[-2,],所以函数f (A)的最大值为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)因为f (A)=2sin =0,
所以2A+=kπ,k∈Z,
所以A=,k∈Z.
因为A∈,所以A=.
在△ABC中,由正弦定理得,====2,
所以b+c=(sin B+sin C)=,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
所以(b+c)2=b2+c2+2bc=6,①
由余弦定理得b2+c2-2bc cos A=a2,
即b2+c2-bc=3,②
由①②解得bc=1,
所以S△ABC=bc sin A=×1×=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
18.(17分)(2025·西安市未央区校级模拟)已知等差数列{an}的首项为1,公差为2.正项数列{bn}的前n项和为Sn,且2Sn=+bn.
(1)求数列{an}和数列{bn}的通项公式;
(2)若cn=,求数列{cn}的前2n项和.
[解] (1)依题意可得an=1+2(n-1)=2n-1,
由2Sn=+bn,得2Sn-1=+bn-1(n≥2),
两式相减得2bn=+bn-bn-1,则(bn+bn-1)(bn-bn-1-1)=0(n≥2),
∵bn>0,∴bn-bn-1=1,
令n=1,得2S1=2b1=+b1,得b1=1或b1=0(舍去),
∴bn=1+(n-1)×1=n,
综上可得,an=2n-1,bn=n.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)由(1)可得cn==,
∴c1+c2+…+c2n=(c1+c3+…+c2n-1)+(c2+c4+…+c2n)=(1+5+…+4n-3)+(22+24+…+
22n)==(2n-1)n+,
∴{cn}的前2n项和为(2n-1)n+.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
19.(17分)已知函数f (x)=-aex,a∈R.
(1)当a=0时,求曲线y=f (x)在x=1处的切线方程;
(2)当a=1时,求f (x)的单调区间和极值;
(3)若对任意x∈R,f (x)≤ex-1恒成立,求实数a的取值范围.
[解] (1)当a=0时,f (x)=,则f ′(x)=,f ′(1)=0,又f (1)=,
所以曲线y=f (x)在x=1处的切线方程为y=.
(2)当a=1时,f (x)=xe-x-ex,则f ′(x)=(1-x)e-x-ex=.
令g(x)=1-x-e2x,则g′(x)=-1-2e2x<0,
故g(x)在R上单调递减,又g(0)=0,
因此0是g(x)在R上的唯一零点,
即0是f′(x)在R上的唯一零点.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
当x变化时,f ′(x),f (x)的变化情况如下表:
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
x (-∞,0) 0 (0,+∞)
f ′(x) + 0 -
f (x) 单调递增 -1 单调递减
所以f (x)的单调递增区间为(-∞,0),单调递减区间为(0,+∞),
f (x)的极大值为f (0)=-1,无极小值.
(3)由题意知xe-x-aex≤ex-1,即a≥,即a≥.
设m(x)=,则m′(x)==,
令m′(x)=0,解得x=,当x∈时,m′(x)>0,m(x)单调递增,当x∈时,m′(x)<0,m(x)单调递减,
所以m(x)max=m==-.
所以a≥-,即实数a的取值范围为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
谢 谢 !
第六章 数列
滚动测试卷(三) 第一~六章
单元检测(一)
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={1,3,a2},B={1,a+2},若B A,则a=( )
A.2 B.1
C.-2 D.-1
A [因为B A,所以a+2=3或a+2=a2.
由a+2=3,得a=1(舍去).
由a+2=a2,得a=-1(舍去)或a=2.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
2.已知复数z满足|z-3+4i|=1,则z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D [由|z-3+4i|=1及复数的几何意义,可得复数z在复平面内对应的点Z(a,b)的轨迹是以(3,-4)为圆心、1为半径的圆,该圆的方程为(a-3)2+(b+4)2=1,所以z在复平面内对应的点位于第四象限.故选D.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
3.记Sn为等比数列{an}的前n项和,若a3a5=2a2a4,则=( )
A.5 B.4
C.3 D.2
C [法一:设等比数列{an}的公比为q,由a3a5=2a2a4,得a1q2·a1q4=2a1q·a1q3,又a1≠0,q≠0,所以q2=2,所以==1+q2=3.故选C.
法二:设等比数列{an}的公比为q,由a3a5=2a2a4,
得a3a5=2a2a4=,
因为a3≠0,所以a5=2a3,
所以q2=2,所以==1+=1+=1+q2=3.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
4.已知平面向量a,b,c满足a+b+c=0,|a|=|b|=1,|c|=,则a与b的夹角为( )
A. B.
C. D.
B [由题意得(a+b)2=2+2a·b=2+2|a||b|·cos 〈a,b〉=2+2cos 〈a,b〉=3,所以cos 〈a,b〉=.
又〈a,b〉∈[0,π],所以〈a,b〉=.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
5.(2025·湖北武汉模拟)已知数列满足a1=-,an+1=1-,则a6=( )
A.- B. C. D.5
B [由题意得a1=-,a2=1-=5,a3=1-=,
a4=1-=-,a5=1-=5,a6=1-=.
故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
6.已知公差为负数的等差数列{an}的前n项和为Sn,若a3,a4,a7是等比数列,则当Sn取最大值时,n=( )
A.2或3 B.2
C.3 D.4
B [设等差数列的公差为d(d<0),则由a3,a4,a7是等比数列,得(a1+3d)2=(a1+2d)(a1+6d),整理得d(2a1+3d)=0,所以2a1+3d=0,即a1=-d,所以Sn=na1+d=n2-2dn=-2d.因为d<0,所以当n=2时,Sn取得最大值-2d.故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
7.已知函数f (x)的部分图象如图所示,则f (x)的解析式可能是( )
A.f (x)=sin (tan x)
B.f (x)=tan (sin x)
C.f (x)=cos (tan x)
D.f (x)=tan (cos x)
D [根据题图可知函数f (x)的图象关于y轴对称,所以函数f (x)为偶函数,且定义域为R.对于A,C,函数f (x)的定义域为,不满足题意,故排除A,C;对于B,f (-x)=tan [sin (-x)]=tan (-sin x)=-tan (sin x)=-f (x),f (x)为奇函数,不满足题意,故排除B.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
8.已知正项数列{an}满足+…+=(n∈N*),若a5-2a6=7,则a1=( )
A. B.1
C. D.2
D [当n=1时,=,即a1a2=3,当n≥2时,由+…+=,得+…+==,以上两式相减,得==,又a1a2=3,所以anan+1=4n2-1(n∈N*),所以a5a6=4×52-1=99,又a5-2a6=7,所以a5=18,a6=.因为a4a5=4×42-1=63,所以a4=.因为a3a4=4×32-1=35,所以a3=10.因为a2a3=4×22-1=15,所以a2=,所以a1=2.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知向量a,b不共线,向量a+b平分a与b的夹角,则下列结论一定正确的是( )
A.a·b=0
B.(a+b)⊥(a-b)
C.向量a与b在a+b上的投影向量相等
D.|a+b|=|a-b|
√
BC [在 ABCD中,令=a,=b,由题意可知, ABCD为菱形,所以||=||,即|a|=|b|,a+b=,a-b=.对于A,因为a·b=|a|·|b|cos 〈a,b〉,所以只有当〈a,b〉=时,才有a·b=0,故A不正确;对于B,由菱形的性质知AC⊥BD,即(a+b)⊥(a-b),故B正确;对于C,因为a2=b2,所以a2+a·b=b2+a·b,即a·(a+b)=b·(a+b),因为a在a+b上的投影向量为·(a+b),b在a+b上的投影向量为·(a+b),所以向量a与b在a+b上的投影向量相等,故C正确;对于D,菱形的对角线不一定相等,故D不正确.综上,故选BC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
10.已知等差数列的前n项和为Sn,正项等比数列的前n项积为Tn,则( )
A.数列是等差数列
B.数列是等比数列
C.数列是等差数列
D.数列是等比数列
√
√
ABD [设的公差为d,的公比为q,
则Sn=n2+n =n+,
所以=是常数,故A正确;
易知==3d是常数,故B正确;
由ln Tn-ln Tn-1=ln bn不是常数,故C错误;
÷==q2是常数,故D正确.
故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
11.已知定义在R上的函数f (x)满足以下条件:①对于任意的x,y∈R,f (x+y)+f (x-y)=2f (x)f (y);②f (0)≠0;③f (k)=0,其中k是正常数.则下列结论正确的是( )
A.f (0)=1
B.f (2k)=1
C.f (x)是偶函数
D.f (x+2k)+f (x)=0
√
√
ACD [f (x+y)+f (x-y)=2f (x)f (y)对任意x,y∈R都成立,
对于A,令x=y=0,得2f (0)=2[f (0)]2,因为f (0)≠0,所以f (0)=1,所以选项A正确;
对于B,令x=y=k,得f (2k)+f (0)=2[f (k)]2,因为f (0)=1,f (k)=0,所以f (2k)=-1,所以选项B错误;
对于C,令x=0,得f (y)+f (-y)=2f (0)f (y),因为f (0)=1,所以f (-y)=
f (y),所以函数f (x)是偶函数,所以选项C正确;
对于D,令y=k,且x+k代换x,得f (x+2k)+f (x)=2f (x+k)f (k),因为
f (k)=0,所以f (x+2k)+f (x)=0,所以选项D正确.综上,故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量a,b,c在网格中的位置如图所示,若网格纸上小正方形的边长为1,则(a-b)·c=________,a·b=________.
2
3
2 3 [建立如图所示的平面直角坐标系,则a=(2,1),b=(2,
-1),c=(0,1),所以a-b=(0,2),a·b=4-1=3,所以(a-b)·c=2.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
13.(2024·盐城调研)写出一个同时满足下列条件①②的等比数列{an}的通项公式an=_________________.
①anan+1<0;②|an|<|an+1|.
(-2)n(答案不唯一)
(-2)n(答案不唯一) [设等比数列{an}的公比为q,
由anan+1<0,可知q<0,
又|an|<|an+1|,所以|q|>1,
所以q<-1,所以q可取-2,
设a1=-2,
则an=-2·(-2)n-1=(-2)n(答案不唯一).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
14.如图为某校数学社团用数学软件制作的“蚊香”.画法如下:在水平直线上取长度为1的线段AB,作一个等边三角形ABC,然后以点B为圆心,AB为半径逆时针画圆弧交线段CB的延长线于点D(第一段圆弧),再以点C为圆心,CD为半径逆时针画圆弧交线段AC的延长线于点E(第二段圆弧),再以点A为圆心,AE为半径逆时针画圆弧……以此类推,当得到的“蚊香”恰好有11段圆弧时,“蚊香”的长度为________.
44π
44π [由题意知每段圆弧所对的圆心角都是,第n段圆弧的半径为n,弧长记为an,
则an=·n,
所以前11段圆弧的长度S11=(1+2+…+11)=44π.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知等差数列{an}的前n项和为Sn,且a4=8,a6=12.
(1)求数列{an}的通项公式;
(2)若Sn=20,求n的值.
[解] (1)∵等差数列{an}的前n项和为Sn,且a4=8,a6=12,
∴解得a1=2,d=2,
∴数列{an}的通项公式an=a1+(n-1)d=2+(n-1)×2=2n.
(2)∵Sn=20,
∴Sn=(a1+an)=(2+2n)=n2+n=20,
解得n=4或n=-5,∵n∈N*,∴n的值为4.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
16.(15分)设数列{an}的前n项和为Sn,an+Sn=1.
(1)求数列{an}的通项公式;
(2)数列{bn}满足anbn=cos ,求{bn}的前50项和T50.
[解] (1)由an+Sn=1,得an-1+Sn-1=1(n≥2),
两式相减得an-an-1+an=0(n≥2),
即an=an-1(n≥2),
当n=1时,2a1=1,得a1=≠0,
所以=(n≥2),故{an}是首项为,公比为的等比数列.
故an=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)由(1)得bn=2n cos ,
所以T50=-22+24-26+28-…-250
=
=-(1+425).
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
17.(15分)在△ABC中,角A,B,C所对的边分别为a,b,c,设向量m=(2sin A,sin A+cos A),n=(cos A,cos A-sin A),f (A)=m·n,A∈.
(1)求函数f (A)的最大值;
(2)若f (A)=0,a=,sin B+sin C=,求△ABC的面积.
[解] 由题知,f (A)=m·n
=(2sin A,sin A+cos A)·(cos A,cos A-sin A)
=2sin A cos A+cos2A-sin2A
=sin2A+cos 2A
=2sin .
因为≤A≤,所以≤2A+,所以-1≤sin ,所以f (A)∈[-2,],所以函数f (A)的最大值为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)因为f (A)=2sin =0,
所以2A+=kπ,k∈Z,
所以A=,k∈Z.
因为A∈,所以A=.
在△ABC中,由正弦定理得,====2,
所以b+c=(sin B+sin C)=,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
所以(b+c)2=b2+c2+2bc=6,①
由余弦定理得b2+c2-2bc cos A=a2,
即b2+c2-bc=3,②
由①②解得bc=1,
所以S△ABC=bc sin A=×1×=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
18.(17分)(2025·西安市未央区校级模拟)已知等差数列{an}的首项为1,公差为2.正项数列{bn}的前n项和为Sn,且2Sn=+bn.
(1)求数列{an}和数列{bn}的通项公式;
(2)若cn=,求数列{cn}的前2n项和.
[解] (1)依题意可得an=1+2(n-1)=2n-1,
由2Sn=+bn,得2Sn-1=+bn-1(n≥2),
两式相减得2bn=+bn-bn-1,则(bn+bn-1)(bn-bn-1-1)=0(n≥2),
∵bn>0,∴bn-bn-1=1,
令n=1,得2S1=2b1=+b1,得b1=1或b1=0(舍去),
∴bn=1+(n-1)×1=n,
综上可得,an=2n-1,bn=n.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)由(1)可得cn==,
∴c1+c2+…+c2n=(c1+c3+…+c2n-1)+(c2+c4+…+c2n)=(1+5+…+4n-3)+(22+24+…+
22n)==(2n-1)n+,
∴{cn}的前2n项和为(2n-1)n+.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
19.(17分)已知函数f (x)=-aex,a∈R.
(1)当a=0时,求曲线y=f (x)在x=1处的切线方程;
(2)当a=1时,求f (x)的单调区间和极值;
(3)若对任意x∈R,f (x)≤ex-1恒成立,求实数a的取值范围.
[解] (1)当a=0时,f (x)=,则f ′(x)=,f ′(1)=0,又f (1)=,
所以曲线y=f (x)在x=1处的切线方程为y=.
(2)当a=1时,f (x)=xe-x-ex,则f ′(x)=(1-x)e-x-ex=.
令g(x)=1-x-e2x,则g′(x)=-1-2e2x<0,
故g(x)在R上单调递减,又g(0)=0,
因此0是g(x)在R上的唯一零点,
即0是f′(x)在R上的唯一零点.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
当x变化时,f ′(x),f (x)的变化情况如下表:
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
x (-∞,0) 0 (0,+∞)
f ′(x) + 0 -
f (x) 单调递增 -1 单调递减
所以f (x)的单调递增区间为(-∞,0),单调递减区间为(0,+∞),
f (x)的极大值为f (0)=-1,无极小值.
(3)由题意知xe-x-aex≤ex-1,即a≥,即a≥.
设m(x)=,则m′(x)==,
令m′(x)=0,解得x=,当x∈时,m′(x)>0,m(x)单调递增,当x∈时,m′(x)<0,m(x)单调递减,
所以m(x)max=m==-.
所以a≥-,即实数a的取值范围为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
谢 谢 !
同课章节目录
