《高考快车道》2026版高三一轮总复习数学(基础版)63 第六章 思维进阶8 数列中的综合问题 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)63 第六章 思维进阶8 数列中的综合问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 09:21:56 | ||
图片预览








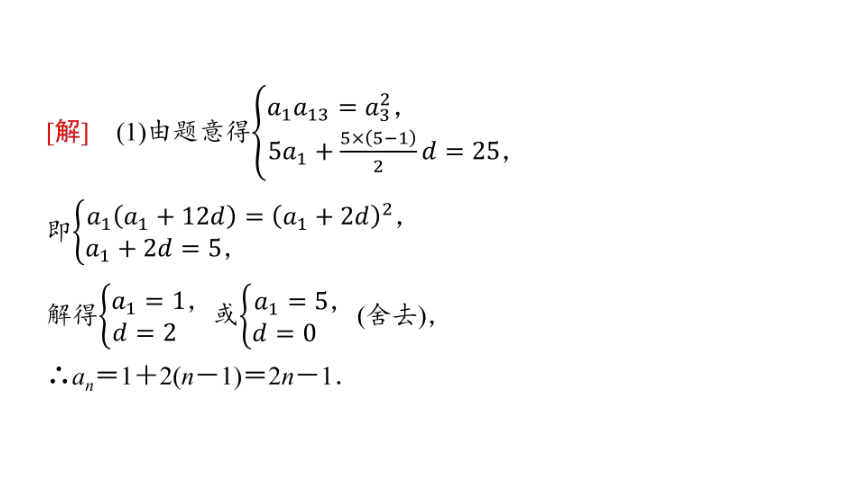
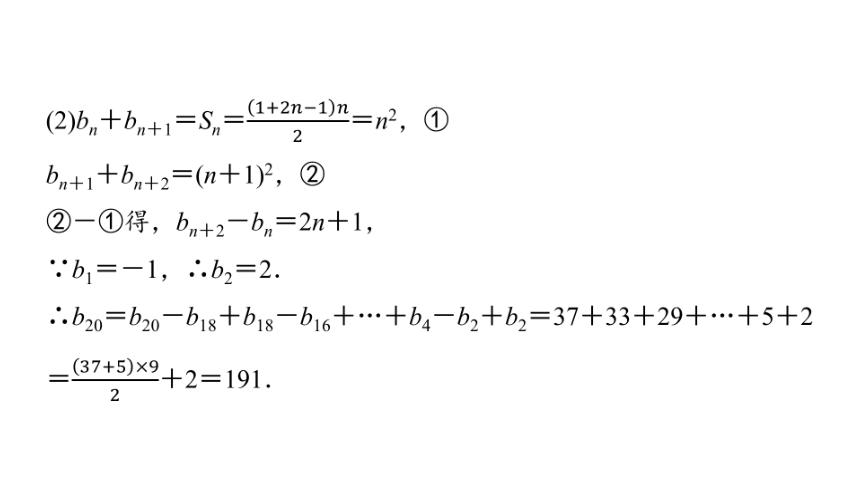


文档简介
(共54张PPT)
第六章 数列
思维进阶8 数列中的综合问题
数列的综合问题、递推数列以及数列与其他知识的交汇问题,是历年高考的热点内容.一般围绕等差数列、等比数列的知识命题,涉及数列的函数性质、通项公式、前n项和公式等.
题型一 等差数列、等比数列的综合问题
[典例1] (2025·连云港模拟)已知等差数列{an}的前n项和为Sn,a2=3,S10=65,数列{bn}的前n项和Tn=2bn-2.
(1)求数列{an}与{bn}的通项公式;[切入点:利用bn=Tn-Tn-1(n≥2)找出bn的递推关系]
[解] ∵等差数列{an}的前n项和为Sn,a2=3,S10=65,
∴解得
∴an=2+(n-1)×1=n+1.
∵Tn=2bn-2,∴Tn-1=2bn-1-2,n≥2,
两式相减得bn=2bn-1,
又∵b1=2b1-2,∴b1=2,
∴{bn}是以2为首项,2为公比的等比数列,
∴bn=2×2n-1=2n.
(2)若cn=anbn,求数列{cn}的前n项和Gn.[关键点:错位相减法求和]
[阅读与思考] 由(1)知cn=(n+1)2n.
∴Gn=2×21+3×22+4×23+…+(n+1)2n,①→({an}为等差数列,{bn}为等比数列,求和用错位相减法)
∴2Gn=2×22+3×23+…+n×2n+(n+1)2n+1,②→(写①②两个表达式时,应特别注意将两式“错项对齐”)
①-②得-Gn=2×21+22+23+…+2n-(n+1)2n+1
=2+-(n+1)2n+1=-n·2n+1,
∴Gn=n·2n+1.→(结果整理)
反思领悟 (1)在应用错位相减法求和时,一定要抓住数列的特征,所谓“错位”相减,就是找“同类项”相减.项数的位置一定不能出错.另外需要注意,本例中等式①的第1项需要保留,等式②的最后一项也一定不能漏掉,中间错位相减的项有(n-1)项.
(2)数列的综合问题常将等差、等比数列结合,两者相互联系、相互转化,解答这类问题的方法:寻找通项公式,利用性质进行转化.
巩固迁移1 (2025·无锡模拟)已知等差数列{an}的前n项和为Sn,公差d≠0,a3是a1,a13的等比中项,S5=25.
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=-1,bn+bn+1=Sn,求b20.
[解] (1)由题意得
即
解得或(舍去),
∴an=1+2(n-1)=2n-1.
(2)bn+bn+1=Sn==n2,①
bn+1+bn+2=(n+1)2,②
②-①得,bn+2-bn=2n+1,
∵b1=-1,∴b2=2.
∴b20=b20-b18+b18-b16+…+b4-b2+b2=37+33+29+…+5+2
=+2=191.
题型二 递推数列
[典例2] (2023·新高考Ⅱ卷)已知{an}为等差数列,bn=
.记Sn,Tn分别为数列{an},{bn}的前n项和,
S4=32,T3=16.
(1)求{an}的通项公式;[切入点:结合已知条件中的S4,T3列方程组]
[解] 设{an}的公差为d,
因为bn=
所以b1=a1-6,b2=2a2=2a1+2d,b3=a3-6=a1+2d-6.
因为S4=32,T3=16,
所以
解得
所以an=2n+3.
(2)证明:当n>5时,Tn>Sn.[关键点:分组求和]
[阅读与思考] 证明:当n为奇数时,
Tn=(a1-6)+2a2+(a3-6)+2a4+…+(an-6)
=(a1-6)+(a3-6)+…+(an-6)+2(a2+a4+…+an-1)
=(a1+a2+…+an)+(a2+a4+…+an-1)-6·
=Sn+-3(n+1)→(如果数列的奇数项、偶数项构成等差或等比数列,则求其前n项和时可以使用分组求和法,使具有相同结构的部分求和,然后将结果相加、化简即可)
=Sn+-3(n+1),
所以Tn-Sn=-3(n+1)
=
=,
所以当n>5时,Tn-Sn>0,即Tn>Sn.
当n为偶数时,
Tn=(a1-6)+2a2+(a3-6)+2a4+…+(an-1-6)+2an
=(a1+a2+…+an)+(a2+a4+…+an)-6·
=Sn+-3n
=Sn+,→(讨论n为偶数的情况,不可遗漏)
所以Tn-Sn=,所以当n>5时,Tn-Sn>0,
即Tn>Sn.
综上所述,当n>5时,Tn>Sn成立.
反思领悟 本例给出的递推数列属于数列奇偶项问题,解决此类问题的关键在于搞清数列奇数项和偶数项的首项、项数、公差或公比等,特别要注意分类讨论思想在解题中的灵活运用.
巩固迁移2 (2024·山东潍坊三模)已知正项等差数列{an}的公差为2,前n项和为Sn,且S1+1,S2,S3+1成等比数列.
(1)求数列{an}的通项公式an;
(2)若bn=求数列{bn}的前4n项和.
[解] (1)因为=(S1+1)(S3+1),
所以(2a1+2)2=(a1+1)(3a1+7),即(a1+1)(a1-3)=0,解得a1=-1或a1=3,
又因为an>0,所以a1=3,
所以an=3+2(n-1)=2n+1.
(2)由(1)知Sn==n(n+2),
所以=,
所以当n为奇数时,b1+b3+…+b4n-1=+…+=+…+=,
当n为偶数时,b4n-2+b4n=S4n-2-S4n=(4n-2)×4n-4n×(4n+2)=-16n,
b2+b4+…+b4n=-16(1+2+…+n)=-8n(n+1),
所以前4n项和T4n=-8n(n+1)=-8n(n+1).
题型三 数列与其他知识的交汇问题
[典例3] (2022·全国乙卷)嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{bn}:b1=1+,b2=1+,b3=1+,…,依此类推,其中αk∈N*(k=1,2,…).则
( )
A.b1C.b6√
[阅读与思考] 法一:当n取奇数时,
由已知b1=1+,b3=1+,
因为>,所以b1>b3,
同理可得b3>b5,b5>b7,…,于是可得b1>b3>b5>b7>…,故A不正确;
当n取偶数时,由已知b2=1+,b4=1+,
因为>,所以b2同理可得b4因为>,所以b1>b2,
同理可得b3>b4,b5>b6,b7>b8,
又因为b3>b7,所以b3>b8,故B不正确;
因为b4b8,
所以b4法二(特殊值法):不妨取αk=1(k=1,2,…),
则b1=1+=2,
b2=1+=1+=1+=,
b3=1+=1+=1+=,
所以b4=1+=1+=,
b5=1+=1+=,
b6=1+=1+=,
b7=1+=1+=,
b8=1+=1+=,
逐一判断选项可知选D.
反思领悟 数列不等式问题常利用数列的单调性,使用放缩法或分离参数法.
巩固迁移3 已知数列{an}满足a1=,an=an-1+(n≥2,n∈N*),若对于任意n∈N*,都有≥an成立,则实数λ的最小值是________.
2
2 [因为当n≥2时,an=an-1+,所以2nan=2n-1an-1+1,
而21a1=3,所以数列{2nan}是首项为3,公差为1的等差数列,
故2nan=n+2,从而an=.
又因为≥an恒成立,
即λ≥恒成立,
所以λ≥.
法一:由(n∈N*,n≥2),
得(n∈N*,n≥2),
得n=2,
所以==2,
所以λ≥2,即实数λ的最小值是2.
法二:令bn=,
则bn+1-bn==,
所以当n=1时,b2>b1;
当n≥2时,bn+1所以当n=2时,bn=取最大值2.
所以λ≥2,即实数λ的最小值是2.]
【教用·备选题】
1.(多选)(2024·江西三模)已知数列{an}满足a1=1,an+1=2an+1,则( )
A.数列{an}是等比数列
B.数列{log2(an+1)}是等差数列
C.数列{an}的前n项和为2n+1-n-2
D.a20能被3整除
√
√
√
BCD [由an+1=2an+1,可得an+1+1=2(an+1),所以数列{an+1}是等比数列,即an=2n-1,
则a1=1,a2=3,a3=7,显然有,所以a1,a2,a3不成等比数列,故选项A错误;
由数列{an+1}是等比数列,可得an+1=2n,即log2(an+1)=log22n=n,故选项B正确;
由an=2n-1,可得前n项和Sn=21-1+22-1+23-1+…+2n-1=-n=2n+1-n-2,故选项C正确;
由a20=220-1=(3-1)20-1=(-1)20-1
=(-1)19],故选项D正确.
故选BCD.]
2.(2025·浦东模拟)在数列1,x,y,15中,若1,x,y成等比数列,且x,y,15成等差数列,则x,y的值分别是
或 [∵1,x,y成等比数列,且x,y,15成等差数列,
∴x2=y,2y=x+15,把y=x2代入2y=x+15,得2x2=x+15,
解得x=3或x=-.当x=3时,y=9,
或
__________________.
此时1,3,9成等比数列,且3,9,15成等差数列,符合题意;
当x=-时,y=,
此时1,-成等比数列,且-,15成等差数列,符合题意.
∴x,y的值分别是或]
3.(2025·河南模拟)已知数列{an}是公差不为零的等差数列,a1=-11,且a2,a5,a6成等比数列.
(1)求{an}的通项公式;
(2)设Sn为{an}的前n项和,求Sn的最小值.
[解] (1)设{an}的公差为d,则a2=-11+d,a5=-11+4d,
a6=-11+5d,
依题意=a2a6,即(-11+4d)2=(-11+d)·(-11+5d),
整理得,11d(d-2)=0,解得d=2或d=0(舍去),
所以an=-11+2(n-1)=2n-13.
(2)由(1)知Sn=×n=×n=n2-12n,
因为Sn=n2-12n=(n-6)2-36≥-36,当且仅当n=6时,等号成立,
所以Sn的最小值为-36.
4.(2025·呼和浩特模拟)甲、乙、丙三名高中生进行传球训练.第一次由甲将球传出,传给乙的概率是,传给丙的概率是;乙传给甲和丙的概率都是;丙传给甲和乙的概率也都是.如此不停地传下去且假定每次传球都能被接到,记开始传球的人为第一次触球者,第n次触球者是甲的概率记为Pn,P1=1.
(1)求P2,P3,P4;
(2)证明:为等比数列.
[解] (1)由题意知,P2=0;
P3==;
P4=P3×0+(1-P3)×=.
(2)证明:当n>1时,Pn=(1-Pn-1)×,Pn-=-,P1-=,
所以数列是首项为,公比为-的等比数列.
5.(2025·衡阳市雁峰区模拟)已知等差数列{an}与等比数列{bn}的前n项和分别为Sn与Tn,且满足==2n-n2-n-1.
(1)若a1=3,求数列{an},{bn}的通项公式;
(2)在(1)的条件下,若cn=求数列{cn}的前2n项的和U2n.
[解] (1)∵=,a1=3,∴==,解得a2=5,
设等差数列{an}的公差为d,则d=a2-a1=2,
∴an=2n+1,∴Sn==n2+2n.
∵=2n-n2-n-1,则Tn=4·2n-4,
设等比数列{bn}的首项为b1,公比为q,
则Tn==qn-,得q=2,b1=4,∴bn=2n+1.
(2)∵cn==
∴U2n=(21+22+…+2n)+
=2(2n-1)+
=2n+1-2+
=2n+1-2+=2n+1+-2,
∴数列{cn}的前2n项的和U2n=2n+1+-2.
进阶训练(八) 数列中的综合问题
1.(2025·广州市越秀区模拟)已知正项等差数列{an}满足3an=a3n,且a4是a3-3与a8的等比中项,则a3=( )
A.3 B.6
C.9 D.12
√
题号
1
3
5
2
4
6
C [设等差数列{an}的公差为d,则an=a1+(n-1)d,
所以a3n=a1+(3n-1)d,又因为3an=a3n,
即3a1+3(n-1)d=a1+(3n-1)d,可得a1=d,
又由(a3-3)a8=,即(a1+2d-3)(a1+7d)=(a1+3d)2,
即(3d-3)(d+7d)=(d+3d)2,即24d2-24d=16d2,
且正项等差数列{an},即d≠0,解得d=3,
所以a3=a1+2d=3d=9.故选C.]
题号
1
3
5
2
4
6
√
2.(多选)(2025·莆田模拟)已知等比数列{an}中,满足a1=1,q=2,则( )
A.数列{a2n}是等比数列
B.数列是递增数列
C.数列{log2an}是等差数列
D.数列{an}中,S10,S20,S30仍成等比数列
√
题号
1
3
5
2
4
6
AC [等比数列{an}中,a1=1,q=2,则an=2n-1,
∴a2n=22n-1,∴数列{a2n}是等比数列,故A正确;
数列是递减数列,故B不正确;
∵log2an=n-1,故数列{log2an}是等差数列,故C正确;
数列{an}中,S10==210-1,S20=220-1,S30=230-1,故D错误.
故选AC.]
题号
1
3
5
2
4
6
3.(2025·青岛模拟)已知等差数列{an}的公差d≠0,首项a1=,a4是a2与a8的等比中项,记Sn为数列{an}的前n项和,则S20=___.
105 [等差数列{an}中,a1=,a4是a2与a8的等比中项,
所以=a2a8,即=,
解得d=或d=0(舍去),所以S20=20×=105.]
105
题号
1
3
5
2
4
6
4.(2024·新余二模)在公差为正数的等差数列{an}中,若a1=3,a3,a6,a8成等比数列,则数列{an}的前10项和为________.
165 [设等差数列{an}的公差为d(d>0),由a1=3,a3,a6,a8成等比数列,可得(3+5d)2=(3+2d)×(3+7d),
整理得8d2-21d-9=0,解得d=3或d=-(舍去),
故等差数列{an}的前10项和S10=10×3+×3=165.]
165
题号
1
3
5
2
4
6
5.(2024·横峰县校级期末)已知Sn为数列{an}的前n项和,且an+2Sn=1.
(1)求数列{an}的通项公式;
(2)设Tn为数列{(2n-1)an}的前n项和,求证:≤Tn<1.
题号
1
3
5
2
4
6
[解] (1)因为an+2Sn=1,当n≥2时,an-1+2Sn-1=1,
两式相减,得an-an-1+2an=0,即an=an-1(n≥2),
又因为a1+2S1=1,即a1=,
所以数列{an}是以为首项,为公比的等比数列,
所以an=.
题号
1
3
5
2
4
6
(2)证明:因为(2n-1)an=,则Tn=+…+,
Tn=+…+,
两式相减得,Tn=+2=+2×=,所以Tn=1-<1,
因为(2n-1)an=>0,所以Tn≥T1=,故≤Tn<1.
题号
1
3
5
2
4
6
6.(2024·黑龙江三模)已知等差数列{an}的公差d>0,a2与a8的等差中项为5,且a4a6=24.
(1)求数列{an}的通项公式;
(2)设bn=求数列{bn}的前20项和T20.
题号
1
3
5
2
4
6
[解] (1)因为{an}为等差数列,且a2与a8的等差中项为5,
所以a2+a8=2×5=2a5,解得a5=5,
因为a4a6=24,
所以(5-d)(5+d)=24,解得d=±1,
因为d>0,所以d=1,
所以an=a5+(n-5)d=5+(n-5)=n,
故数列{an}的通项公式为an=n.
题号
1
3
5
2
4
6
(2)由题知,bn=
即bn=
所以T20=b1+b2+b3+b4+…+b19+b20
=1++3++…+19+
==100+=,
故数列{bn}的前20项和T20为.
题号
1
3
5
2
4
6
谢 谢 !
第六章 数列
思维进阶8 数列中的综合问题
数列的综合问题、递推数列以及数列与其他知识的交汇问题,是历年高考的热点内容.一般围绕等差数列、等比数列的知识命题,涉及数列的函数性质、通项公式、前n项和公式等.
题型一 等差数列、等比数列的综合问题
[典例1] (2025·连云港模拟)已知等差数列{an}的前n项和为Sn,a2=3,S10=65,数列{bn}的前n项和Tn=2bn-2.
(1)求数列{an}与{bn}的通项公式;[切入点:利用bn=Tn-Tn-1(n≥2)找出bn的递推关系]
[解] ∵等差数列{an}的前n项和为Sn,a2=3,S10=65,
∴解得
∴an=2+(n-1)×1=n+1.
∵Tn=2bn-2,∴Tn-1=2bn-1-2,n≥2,
两式相减得bn=2bn-1,
又∵b1=2b1-2,∴b1=2,
∴{bn}是以2为首项,2为公比的等比数列,
∴bn=2×2n-1=2n.
(2)若cn=anbn,求数列{cn}的前n项和Gn.[关键点:错位相减法求和]
[阅读与思考] 由(1)知cn=(n+1)2n.
∴Gn=2×21+3×22+4×23+…+(n+1)2n,①→({an}为等差数列,{bn}为等比数列,求和用错位相减法)
∴2Gn=2×22+3×23+…+n×2n+(n+1)2n+1,②→(写①②两个表达式时,应特别注意将两式“错项对齐”)
①-②得-Gn=2×21+22+23+…+2n-(n+1)2n+1
=2+-(n+1)2n+1=-n·2n+1,
∴Gn=n·2n+1.→(结果整理)
反思领悟 (1)在应用错位相减法求和时,一定要抓住数列的特征,所谓“错位”相减,就是找“同类项”相减.项数的位置一定不能出错.另外需要注意,本例中等式①的第1项需要保留,等式②的最后一项也一定不能漏掉,中间错位相减的项有(n-1)项.
(2)数列的综合问题常将等差、等比数列结合,两者相互联系、相互转化,解答这类问题的方法:寻找通项公式,利用性质进行转化.
巩固迁移1 (2025·无锡模拟)已知等差数列{an}的前n项和为Sn,公差d≠0,a3是a1,a13的等比中项,S5=25.
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=-1,bn+bn+1=Sn,求b20.
[解] (1)由题意得
即
解得或(舍去),
∴an=1+2(n-1)=2n-1.
(2)bn+bn+1=Sn==n2,①
bn+1+bn+2=(n+1)2,②
②-①得,bn+2-bn=2n+1,
∵b1=-1,∴b2=2.
∴b20=b20-b18+b18-b16+…+b4-b2+b2=37+33+29+…+5+2
=+2=191.
题型二 递推数列
[典例2] (2023·新高考Ⅱ卷)已知{an}为等差数列,bn=
.记Sn,Tn分别为数列{an},{bn}的前n项和,
S4=32,T3=16.
(1)求{an}的通项公式;[切入点:结合已知条件中的S4,T3列方程组]
[解] 设{an}的公差为d,
因为bn=
所以b1=a1-6,b2=2a2=2a1+2d,b3=a3-6=a1+2d-6.
因为S4=32,T3=16,
所以
解得
所以an=2n+3.
(2)证明:当n>5时,Tn>Sn.[关键点:分组求和]
[阅读与思考] 证明:当n为奇数时,
Tn=(a1-6)+2a2+(a3-6)+2a4+…+(an-6)
=(a1-6)+(a3-6)+…+(an-6)+2(a2+a4+…+an-1)
=(a1+a2+…+an)+(a2+a4+…+an-1)-6·
=Sn+-3(n+1)→(如果数列的奇数项、偶数项构成等差或等比数列,则求其前n项和时可以使用分组求和法,使具有相同结构的部分求和,然后将结果相加、化简即可)
=Sn+-3(n+1),
所以Tn-Sn=-3(n+1)
=
=,
所以当n>5时,Tn-Sn>0,即Tn>Sn.
当n为偶数时,
Tn=(a1-6)+2a2+(a3-6)+2a4+…+(an-1-6)+2an
=(a1+a2+…+an)+(a2+a4+…+an)-6·
=Sn+-3n
=Sn+,→(讨论n为偶数的情况,不可遗漏)
所以Tn-Sn=,所以当n>5时,Tn-Sn>0,
即Tn>Sn.
综上所述,当n>5时,Tn>Sn成立.
反思领悟 本例给出的递推数列属于数列奇偶项问题,解决此类问题的关键在于搞清数列奇数项和偶数项的首项、项数、公差或公比等,特别要注意分类讨论思想在解题中的灵活运用.
巩固迁移2 (2024·山东潍坊三模)已知正项等差数列{an}的公差为2,前n项和为Sn,且S1+1,S2,S3+1成等比数列.
(1)求数列{an}的通项公式an;
(2)若bn=求数列{bn}的前4n项和.
[解] (1)因为=(S1+1)(S3+1),
所以(2a1+2)2=(a1+1)(3a1+7),即(a1+1)(a1-3)=0,解得a1=-1或a1=3,
又因为an>0,所以a1=3,
所以an=3+2(n-1)=2n+1.
(2)由(1)知Sn==n(n+2),
所以=,
所以当n为奇数时,b1+b3+…+b4n-1=+…+=+…+=,
当n为偶数时,b4n-2+b4n=S4n-2-S4n=(4n-2)×4n-4n×(4n+2)=-16n,
b2+b4+…+b4n=-16(1+2+…+n)=-8n(n+1),
所以前4n项和T4n=-8n(n+1)=-8n(n+1).
题型三 数列与其他知识的交汇问题
[典例3] (2022·全国乙卷)嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{bn}:b1=1+,b2=1+,b3=1+,…,依此类推,其中αk∈N*(k=1,2,…).则
( )
A.b1
[阅读与思考] 法一:当n取奇数时,
由已知b1=1+,b3=1+,
因为>,所以b1>b3,
同理可得b3>b5,b5>b7,…,于是可得b1>b3>b5>b7>…,故A不正确;
当n取偶数时,由已知b2=1+,b4=1+,
因为>,所以b2
同理可得b3>b4,b5>b6,b7>b8,
又因为b3>b7,所以b3>b8,故B不正确;
因为b4
所以b4
则b1=1+=2,
b2=1+=1+=1+=,
b3=1+=1+=1+=,
所以b4=1+=1+=,
b5=1+=1+=,
b6=1+=1+=,
b7=1+=1+=,
b8=1+=1+=,
逐一判断选项可知选D.
反思领悟 数列不等式问题常利用数列的单调性,使用放缩法或分离参数法.
巩固迁移3 已知数列{an}满足a1=,an=an-1+(n≥2,n∈N*),若对于任意n∈N*,都有≥an成立,则实数λ的最小值是________.
2
2 [因为当n≥2时,an=an-1+,所以2nan=2n-1an-1+1,
而21a1=3,所以数列{2nan}是首项为3,公差为1的等差数列,
故2nan=n+2,从而an=.
又因为≥an恒成立,
即λ≥恒成立,
所以λ≥.
法一:由(n∈N*,n≥2),
得(n∈N*,n≥2),
得n=2,
所以==2,
所以λ≥2,即实数λ的最小值是2.
法二:令bn=,
则bn+1-bn==,
所以当n=1时,b2>b1;
当n≥2时,bn+1
所以λ≥2,即实数λ的最小值是2.]
【教用·备选题】
1.(多选)(2024·江西三模)已知数列{an}满足a1=1,an+1=2an+1,则( )
A.数列{an}是等比数列
B.数列{log2(an+1)}是等差数列
C.数列{an}的前n项和为2n+1-n-2
D.a20能被3整除
√
√
√
BCD [由an+1=2an+1,可得an+1+1=2(an+1),所以数列{an+1}是等比数列,即an=2n-1,
则a1=1,a2=3,a3=7,显然有,所以a1,a2,a3不成等比数列,故选项A错误;
由数列{an+1}是等比数列,可得an+1=2n,即log2(an+1)=log22n=n,故选项B正确;
由an=2n-1,可得前n项和Sn=21-1+22-1+23-1+…+2n-1=-n=2n+1-n-2,故选项C正确;
由a20=220-1=(3-1)20-1=(-1)20-1
=(-1)19],故选项D正确.
故选BCD.]
2.(2025·浦东模拟)在数列1,x,y,15中,若1,x,y成等比数列,且x,y,15成等差数列,则x,y的值分别是
或 [∵1,x,y成等比数列,且x,y,15成等差数列,
∴x2=y,2y=x+15,把y=x2代入2y=x+15,得2x2=x+15,
解得x=3或x=-.当x=3时,y=9,
或
__________________.
此时1,3,9成等比数列,且3,9,15成等差数列,符合题意;
当x=-时,y=,
此时1,-成等比数列,且-,15成等差数列,符合题意.
∴x,y的值分别是或]
3.(2025·河南模拟)已知数列{an}是公差不为零的等差数列,a1=-11,且a2,a5,a6成等比数列.
(1)求{an}的通项公式;
(2)设Sn为{an}的前n项和,求Sn的最小值.
[解] (1)设{an}的公差为d,则a2=-11+d,a5=-11+4d,
a6=-11+5d,
依题意=a2a6,即(-11+4d)2=(-11+d)·(-11+5d),
整理得,11d(d-2)=0,解得d=2或d=0(舍去),
所以an=-11+2(n-1)=2n-13.
(2)由(1)知Sn=×n=×n=n2-12n,
因为Sn=n2-12n=(n-6)2-36≥-36,当且仅当n=6时,等号成立,
所以Sn的最小值为-36.
4.(2025·呼和浩特模拟)甲、乙、丙三名高中生进行传球训练.第一次由甲将球传出,传给乙的概率是,传给丙的概率是;乙传给甲和丙的概率都是;丙传给甲和乙的概率也都是.如此不停地传下去且假定每次传球都能被接到,记开始传球的人为第一次触球者,第n次触球者是甲的概率记为Pn,P1=1.
(1)求P2,P3,P4;
(2)证明:为等比数列.
[解] (1)由题意知,P2=0;
P3==;
P4=P3×0+(1-P3)×=.
(2)证明:当n>1时,Pn=(1-Pn-1)×,Pn-=-,P1-=,
所以数列是首项为,公比为-的等比数列.
5.(2025·衡阳市雁峰区模拟)已知等差数列{an}与等比数列{bn}的前n项和分别为Sn与Tn,且满足==2n-n2-n-1.
(1)若a1=3,求数列{an},{bn}的通项公式;
(2)在(1)的条件下,若cn=求数列{cn}的前2n项的和U2n.
[解] (1)∵=,a1=3,∴==,解得a2=5,
设等差数列{an}的公差为d,则d=a2-a1=2,
∴an=2n+1,∴Sn==n2+2n.
∵=2n-n2-n-1,则Tn=4·2n-4,
设等比数列{bn}的首项为b1,公比为q,
则Tn==qn-,得q=2,b1=4,∴bn=2n+1.
(2)∵cn==
∴U2n=(21+22+…+2n)+
=2(2n-1)+
=2n+1-2+
=2n+1-2+=2n+1+-2,
∴数列{cn}的前2n项的和U2n=2n+1+-2.
进阶训练(八) 数列中的综合问题
1.(2025·广州市越秀区模拟)已知正项等差数列{an}满足3an=a3n,且a4是a3-3与a8的等比中项,则a3=( )
A.3 B.6
C.9 D.12
√
题号
1
3
5
2
4
6
C [设等差数列{an}的公差为d,则an=a1+(n-1)d,
所以a3n=a1+(3n-1)d,又因为3an=a3n,
即3a1+3(n-1)d=a1+(3n-1)d,可得a1=d,
又由(a3-3)a8=,即(a1+2d-3)(a1+7d)=(a1+3d)2,
即(3d-3)(d+7d)=(d+3d)2,即24d2-24d=16d2,
且正项等差数列{an},即d≠0,解得d=3,
所以a3=a1+2d=3d=9.故选C.]
题号
1
3
5
2
4
6
√
2.(多选)(2025·莆田模拟)已知等比数列{an}中,满足a1=1,q=2,则( )
A.数列{a2n}是等比数列
B.数列是递增数列
C.数列{log2an}是等差数列
D.数列{an}中,S10,S20,S30仍成等比数列
√
题号
1
3
5
2
4
6
AC [等比数列{an}中,a1=1,q=2,则an=2n-1,
∴a2n=22n-1,∴数列{a2n}是等比数列,故A正确;
数列是递减数列,故B不正确;
∵log2an=n-1,故数列{log2an}是等差数列,故C正确;
数列{an}中,S10==210-1,S20=220-1,S30=230-1,故D错误.
故选AC.]
题号
1
3
5
2
4
6
3.(2025·青岛模拟)已知等差数列{an}的公差d≠0,首项a1=,a4是a2与a8的等比中项,记Sn为数列{an}的前n项和,则S20=___.
105 [等差数列{an}中,a1=,a4是a2与a8的等比中项,
所以=a2a8,即=,
解得d=或d=0(舍去),所以S20=20×=105.]
105
题号
1
3
5
2
4
6
4.(2024·新余二模)在公差为正数的等差数列{an}中,若a1=3,a3,a6,a8成等比数列,则数列{an}的前10项和为________.
165 [设等差数列{an}的公差为d(d>0),由a1=3,a3,a6,a8成等比数列,可得(3+5d)2=(3+2d)×(3+7d),
整理得8d2-21d-9=0,解得d=3或d=-(舍去),
故等差数列{an}的前10项和S10=10×3+×3=165.]
165
题号
1
3
5
2
4
6
5.(2024·横峰县校级期末)已知Sn为数列{an}的前n项和,且an+2Sn=1.
(1)求数列{an}的通项公式;
(2)设Tn为数列{(2n-1)an}的前n项和,求证:≤Tn<1.
题号
1
3
5
2
4
6
[解] (1)因为an+2Sn=1,当n≥2时,an-1+2Sn-1=1,
两式相减,得an-an-1+2an=0,即an=an-1(n≥2),
又因为a1+2S1=1,即a1=,
所以数列{an}是以为首项,为公比的等比数列,
所以an=.
题号
1
3
5
2
4
6
(2)证明:因为(2n-1)an=,则Tn=+…+,
Tn=+…+,
两式相减得,Tn=+2=+2×=,所以Tn=1-<1,
因为(2n-1)an=>0,所以Tn≥T1=,故≤Tn<1.
题号
1
3
5
2
4
6
6.(2024·黑龙江三模)已知等差数列{an}的公差d>0,a2与a8的等差中项为5,且a4a6=24.
(1)求数列{an}的通项公式;
(2)设bn=求数列{bn}的前20项和T20.
题号
1
3
5
2
4
6
[解] (1)因为{an}为等差数列,且a2与a8的等差中项为5,
所以a2+a8=2×5=2a5,解得a5=5,
因为a4a6=24,
所以(5-d)(5+d)=24,解得d=±1,
因为d>0,所以d=1,
所以an=a5+(n-5)d=5+(n-5)=n,
故数列{an}的通项公式为an=n.
题号
1
3
5
2
4
6
(2)由题知,bn=
即bn=
所以T20=b1+b2+b3+b4+…+b19+b20
=1++3++…+19+
==100+=,
故数列{bn}的前20项和T20为.
题号
1
3
5
2
4
6
谢 谢 !
同课章节目录
