1.3.1函数单调性与导数 教学设计
文档属性
| 名称 | 1.3.1函数单调性与导数 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 169.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 10:14:21 | ||
图片预览

文档简介
1.3.1函数的单调性与导数
【教学目标】
1.探索函数的单调性与导数的关系
2.会利用导数判断函数的单调性并求函数的单调区间
3.通过本节的学习,掌握用导数研究单调性的方法
4.在探索过程中培养学生的观察、分析、概括的能力渗透数形结合思想、转化思想。
5.通过在教学过程中让学生多动手、多观察、勤思考、善总结,培养学生的
探索精神,引导学生养成自主学习的学习习惯。
【教学重点难点】
教学重点:探索并应用函数的单调性与导数的关系求单调区间。
教学难点:探索函数的单调性与导数的关系。
【教 具】多媒体
【教学方法】 “124”模式 问题启发式
【教学过程】
一.复习回顾(学生回答)
复习 1:基本初等函数的导数公式
复习2:函数单调性的定义,判断单调性的方法,(图像法,定义法)
问题提出:
那么如何判断的单调性呢?(后面例题中详讲)引导学生图像法,定义去尝试发觉有困难,引出课题:板书课题:函数的单调性与导数
二.新知探究
探究任务一:函数单调性与其导数的关系:
问题1:如图(1)表示高台跳水运动员的高度h随时间t变化的函数的图像,图(2)表示高台跳水运动员的速度h的图像.
通过观察图像, 运动员从起跳到最高点,以及从
最高点到入水这两段时间的运动状态有什么区别?
此时你能发现这两个函数图像有什么联系吗
(分组讨论)
启发: 函数在(0,a)上位增函数,函数在(0,a)上有何特点呢?函数在(a,b)上为减函数,那么函数在(a,b)上有何特点呢?
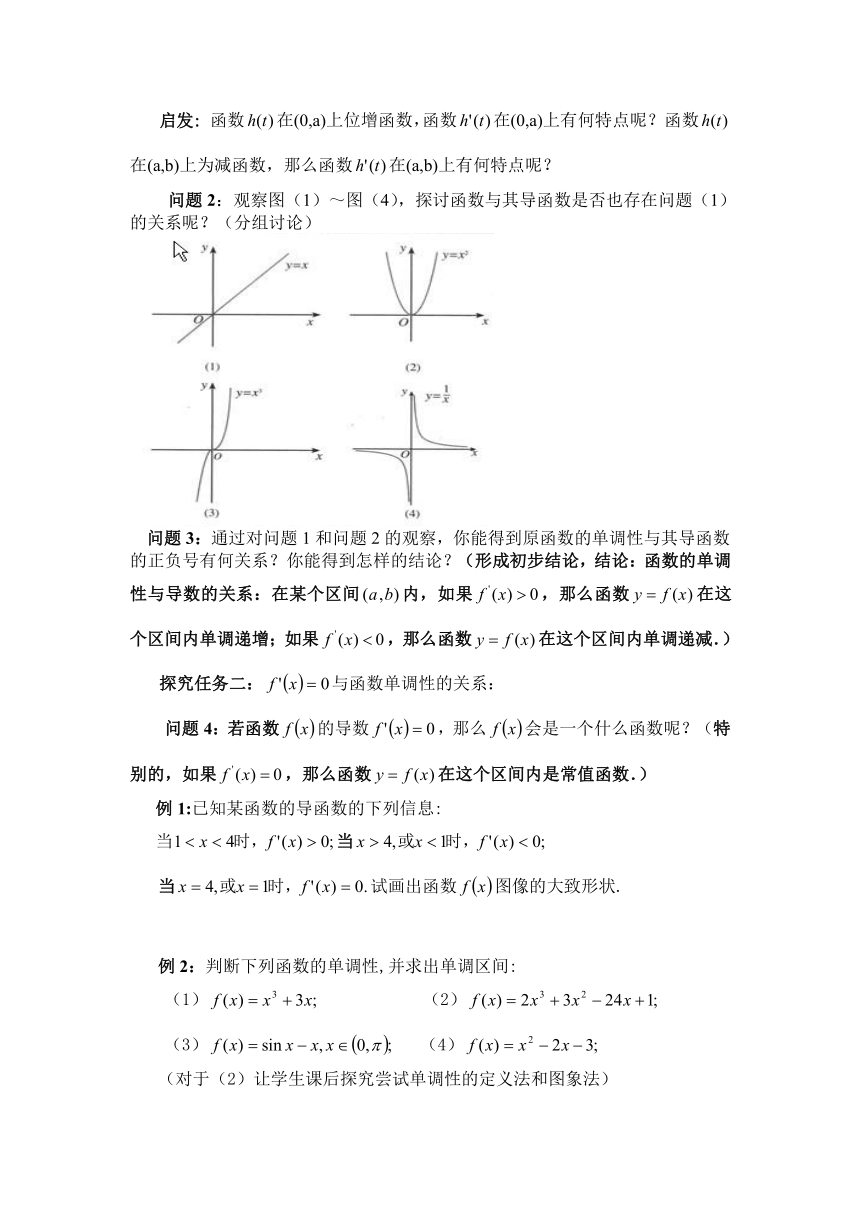
问题2:观察图(1)~图(4),探讨函数与其导函数是否也存在问题(1)的关系呢?(分组讨论)
问题3:通过对问题1和问题2的观察,你能得到原函数的单调性与其导函数的正负号有何关系?你能得到怎样的结论?(形成初步结论,结论:函数的单调性与导数的关系:在某个区间内,如果,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减.)
探究任务二:与函数单调性的关系:
问题4:若函数的导数,那么会是一个什么函数呢?(特别的,如果,那么函数在这个区间内是常值函数.)
例1:已知某函数的导函数的下列信息:
当当
当试画出函数图像的大致形状.
例2:判断下列函数的单调性,并求出单调区间:
(1) (2)
(3) (4)
(对于(2)让学生课后探究尝试单调性的定义法和图象法)
问:你对利用导数去研究函数的单调性有什么看法 你能总结出利用导数求单调区间的步骤吗?(简单易行)
“求解函数单调区间的步骤:
(1)确定函数的定义域;(2)求导数;
(3)解不等式,解集在定义域内的部分为增区间;
(4)解不等式,解集在定义域内的部分为减区间.
问题5:导数能帮助我们简洁的求出单调区间,画出大致图象,但我们知道就是递增(递减)也有快与慢的区别,在导数上如何体现呢?下面我们就来看一下下面这个问题
例3.如图1.3-6,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度与时间的函数关系图像.
分析:
在导数几何意义那节我们就感受了增加与减少也由快慢之分,那么我们以容器(2)为例,由于容器上细下粗,所以水以常速注入时,开始阶段高度增加得慢,以后高度增加得越来越快.反映在图像上,(A)符合上述变化情况.同理可知其它三种容器的情况.
解:
思考:例3表明,通过函数图像,不仅可以看出函数的增减,还可以看出其变化的快慢.结合图像,你能从导数的角度解释变化快慢的情况吗?
一般的,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化的快,这时,函数的图像就比较“陡峭”;反之,函数的图像就“平缓”一些.
三,当堂自测
1.求证:函数在(0,2)内是减函数。
2.求下列函数的单调区间:
(1)y=x-lnx; (2)y=.
(3)f(x)=x3+; (4)f(x)=sinx(1+cosx)(0≤x≤2π).
四,课堂小结
1.函数导数与单调性的关系:若函数y=f(x)在某个区间内可导,
如果f ′(x)>0, 则f(x)为增函数;如果f′(x)<0, 则f(x)为减函数.
2.掌握求单调区间的步骤
五,作业设计
课本26页,练习1,2,3,4
六,课后反思
本节课由于提前撰写了教学设计,并且经过了精心的修改,通过课堂教学的实施,能够把新课标理念渗透到教学中去,体现了以学生为主体,以教师为主导的作用发挥的比较到位,学生能极思考,思维敏捷,合作学习氛围浓厚,是一堂成功的教学设计课。
本节课存在的不足之处是:
教学引入时间较长,致使整堂课时间安排显得前松后紧。
教态不够自然、大方;显得过于紧张。
3、改进的思路:①在引导学生提问时,问题要简明扼要。
②多进行公开课,锻炼自己的胆量和语言表达能力。
附:板书设计
函数的单调性与导数
函数单调性与导数的关系利用导数求单调性的步骤 例题讲解例2: 学生板演
【教学目标】
1.探索函数的单调性与导数的关系
2.会利用导数判断函数的单调性并求函数的单调区间
3.通过本节的学习,掌握用导数研究单调性的方法
4.在探索过程中培养学生的观察、分析、概括的能力渗透数形结合思想、转化思想。
5.通过在教学过程中让学生多动手、多观察、勤思考、善总结,培养学生的
探索精神,引导学生养成自主学习的学习习惯。
【教学重点难点】
教学重点:探索并应用函数的单调性与导数的关系求单调区间。
教学难点:探索函数的单调性与导数的关系。
【教 具】多媒体
【教学方法】 “124”模式 问题启发式
【教学过程】
一.复习回顾(学生回答)
复习 1:基本初等函数的导数公式
复习2:函数单调性的定义,判断单调性的方法,(图像法,定义法)
问题提出:
那么如何判断的单调性呢?(后面例题中详讲)引导学生图像法,定义去尝试发觉有困难,引出课题:板书课题:函数的单调性与导数
二.新知探究
探究任务一:函数单调性与其导数的关系:
问题1:如图(1)表示高台跳水运动员的高度h随时间t变化的函数的图像,图(2)表示高台跳水运动员的速度h的图像.
通过观察图像, 运动员从起跳到最高点,以及从
最高点到入水这两段时间的运动状态有什么区别?
此时你能发现这两个函数图像有什么联系吗
(分组讨论)
启发: 函数在(0,a)上位增函数,函数在(0,a)上有何特点呢?函数在(a,b)上为减函数,那么函数在(a,b)上有何特点呢?
问题2:观察图(1)~图(4),探讨函数与其导函数是否也存在问题(1)的关系呢?(分组讨论)
问题3:通过对问题1和问题2的观察,你能得到原函数的单调性与其导函数的正负号有何关系?你能得到怎样的结论?(形成初步结论,结论:函数的单调性与导数的关系:在某个区间内,如果,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减.)
探究任务二:与函数单调性的关系:
问题4:若函数的导数,那么会是一个什么函数呢?(特别的,如果,那么函数在这个区间内是常值函数.)
例1:已知某函数的导函数的下列信息:
当当
当试画出函数图像的大致形状.
例2:判断下列函数的单调性,并求出单调区间:
(1) (2)
(3) (4)
(对于(2)让学生课后探究尝试单调性的定义法和图象法)
问:你对利用导数去研究函数的单调性有什么看法 你能总结出利用导数求单调区间的步骤吗?(简单易行)
“求解函数单调区间的步骤:
(1)确定函数的定义域;(2)求导数;
(3)解不等式,解集在定义域内的部分为增区间;
(4)解不等式,解集在定义域内的部分为减区间.
问题5:导数能帮助我们简洁的求出单调区间,画出大致图象,但我们知道就是递增(递减)也有快与慢的区别,在导数上如何体现呢?下面我们就来看一下下面这个问题
例3.如图1.3-6,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度与时间的函数关系图像.
分析:
在导数几何意义那节我们就感受了增加与减少也由快慢之分,那么我们以容器(2)为例,由于容器上细下粗,所以水以常速注入时,开始阶段高度增加得慢,以后高度增加得越来越快.反映在图像上,(A)符合上述变化情况.同理可知其它三种容器的情况.
解:
思考:例3表明,通过函数图像,不仅可以看出函数的增减,还可以看出其变化的快慢.结合图像,你能从导数的角度解释变化快慢的情况吗?
一般的,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化的快,这时,函数的图像就比较“陡峭”;反之,函数的图像就“平缓”一些.
三,当堂自测
1.求证:函数在(0,2)内是减函数。
2.求下列函数的单调区间:
(1)y=x-lnx; (2)y=.
(3)f(x)=x3+; (4)f(x)=sinx(1+cosx)(0≤x≤2π).
四,课堂小结
1.函数导数与单调性的关系:若函数y=f(x)在某个区间内可导,
如果f ′(x)>0, 则f(x)为增函数;如果f′(x)<0, 则f(x)为减函数.
2.掌握求单调区间的步骤
五,作业设计
课本26页,练习1,2,3,4
六,课后反思
本节课由于提前撰写了教学设计,并且经过了精心的修改,通过课堂教学的实施,能够把新课标理念渗透到教学中去,体现了以学生为主体,以教师为主导的作用发挥的比较到位,学生能极思考,思维敏捷,合作学习氛围浓厚,是一堂成功的教学设计课。
本节课存在的不足之处是:
教学引入时间较长,致使整堂课时间安排显得前松后紧。
教态不够自然、大方;显得过于紧张。
3、改进的思路:①在引导学生提问时,问题要简明扼要。
②多进行公开课,锻炼自己的胆量和语言表达能力。
附:板书设计
函数的单调性与导数
函数单调性与导数的关系利用导数求单调性的步骤 例题讲解例2: 学生板演
同课章节目录
