1.2科学测量(第二课时)同步练习(含解析)
文档属性
| 名称 | 1.2科学测量(第二课时)同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 352.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2025-07-03 15:44:04 | ||
图片预览



文档简介
1.2科学测量(第二课时)同步练习
一.选择题(共10小题)
1.一次国王故意为难阿凡提,他在众臣面前一定要让阿凡提说出眼前池塘里的水有多少桶,阿凡提略加思索后回答:若桶像池塘一样大的话,池塘里的水就只有一桶;若桶只有池塘的十分之一大的话,池塘里的水就有十桶。这则故事说明了( )
A.测量总是有误差的
B.测量的准确程度由最小刻度决定
C.测量的标准不一样,结果也不一样
D.测量工具的量程决定了物体的大小
2.一个量筒中有40mL水,当里面放入一木块,且木块的一半浸入水中时,量筒的读数是49mL,则这块木块的体积是( )
A.8cm3 B.18mL C.18dm3 D.18cm3
3.在用量筒测石块体积的步骤中,正确序号排列为( )
①将适量水注入量筒中读出体积V2
②计算石块体积为V=V1﹣V2
③用细线系住石块放入量筒水中
④读出石块和水的总体积V1
A.①③④② B.④②③① C.③①④② D.③④①②
4.甲、乙两个量筒的分度值分别是2mL和1mL,用它们来测量等质量煤油的体积,如图所示。某同学的读数分别是13.8mL和13.9mL。则下列分析正确的是( )
A.甲量筒的分度值是1cm3
B.两次读数不同是因为煤油体积不同
C.两量筒的分度值不同,不影响误差大小
D.乙量筒的分度值小,因此精确度更高
5.某同学在用量筒量取液体时,先用仰视读得液体体积为34毫升,倒出一部分液体后,再用俯视读得液体体积为15毫升,则倒出的液体体积是( )
A.等于19mL B.小于19mL C.大于19mL D.无法判断
6.实验室在测固体密度时,需用量筒测出固体的体积,如果固体的密度小于水,而不能在水中下沉,我们常用如图的方法即“沉坠法”测出它的体积。如图所示是用量筒测量蜡块体积的过程,则蜡块的体积为(V1、V2、V3为当前水和物体的总体积)( )
A.V3﹣V1 B.V3﹣V2﹣V1 C.V3﹣V2 D.V2﹣V1
7.用量筒和水测小石块体积时,先在量筒内注入适量的水。“适量”的标准是( )
A.看上去不多也不少
B.能淹没石块,且石块放入水中后水不会溢出
C.水面约在量筒中间
D.能淹没石块,且石块放入水中后水不超过量程
8.量筒做得细而高,不做成粗而矮的形状,主要原因是( )
A.细高的量筒便于操作
B.细高的量筒可以做出相对较大的底座,增加稳度
C.细高的量筒与粗矮的量筒相比,相应的刻度间隔较大,能较准确地读数
D.粗矮量筒中的液体较多,筒壁所受压力较大,需用较厚的玻璃,因而不便读数
9.在量筒中注入适量的水,读出水面所对应的刻度值V1如图①所示;将铁块放入量筒中水面所对应的刻度值V2如图②所示;取出铁块,再将物块轻轻地放入水中,静止时如图③所示,水面所对应的刻度值为V3;将铁块和物块系在一起放入量筒中如图④所示,水面所对应的刻度值为V4。则物块的体积V的大小应该是( )
A.V2﹣V1 B.V3﹣V1 C.V4﹣V2 D.V4﹣V3
10.某注射用蒸馏水瓶,按图甲放置测得底面直径为D,液面高度为H1;按图乙放置,测得空间的高度为H2。若瓶子厚度不计,那么该瓶的容积为多大( )
A.DH1H2
B.D2(H1+H2)
C.
D.
二.填空题(共9小题)
11.(1)如图甲所示,木块的测量值是 cm。
(2)用10mL量筒量取液体如图乙所示,则液体的体积为 mL。
12.如图所示为家用自来水表的表盘,其测量的物理量是 ,其读数为 。
13.实验室用排水法测量形状不规则的小石块体积时,老师总是强调先要在量筒中加入“适量的水”。
(1)“适量”是指能用排水法测量出小石块体积的水量范围,其中最多水量是指小石块放入量筒后,会使液面上升到最大刻度线处的水量;最少水量是指小石块放入量筒后,量筒内的液面满足 的水量。
(2)现有100毫升的量筒,用排水法测出体积为15立方厘米的形状不规则的小石块,需加入“适量的水”的体积合适是 。
A.5毫升 B.50毫升 C.80毫升 D.95毫升
14.用量筒测量小石块的体积。甲同学的做法是:在量筒里注入适量的水,记下水的体积V1,然后轻轻放入石块,使量筒里的水完全浸没石块,记下此时水及石块的体积V2,计算石块的体积为V2﹣V1。
(1)如图所示,甲同学所用量筒的最小刻度是 ,小石块的体积是 。
(2)甲同学下列操作,可导致测量结果偏小的是 。
A.石块浸入水中深度过大
B.放入石块后,仰视读数
C.投入石块,有水滴飞溅出来
D.改用粗线拴住石块
15.小明看到一个自来水龙头没有关紧,水一滴一滴断断续续地滴落在地上。他想这个水龙头一昼夜要浪费多少水啊!为了测量水龙头一昼夜浪费的水量,他找来了秒表、量筒。将量筒放在水龙头下,当听到水滴滴在量筒里的声音时开启秒表,并数“1”。一直数到“40”时,按下秒表停止计时,读出秒表的示数为12秒,量筒里水的体积是10mL。则每一滴水的体积为 ,一昼夜流失的水的体积约为 L。
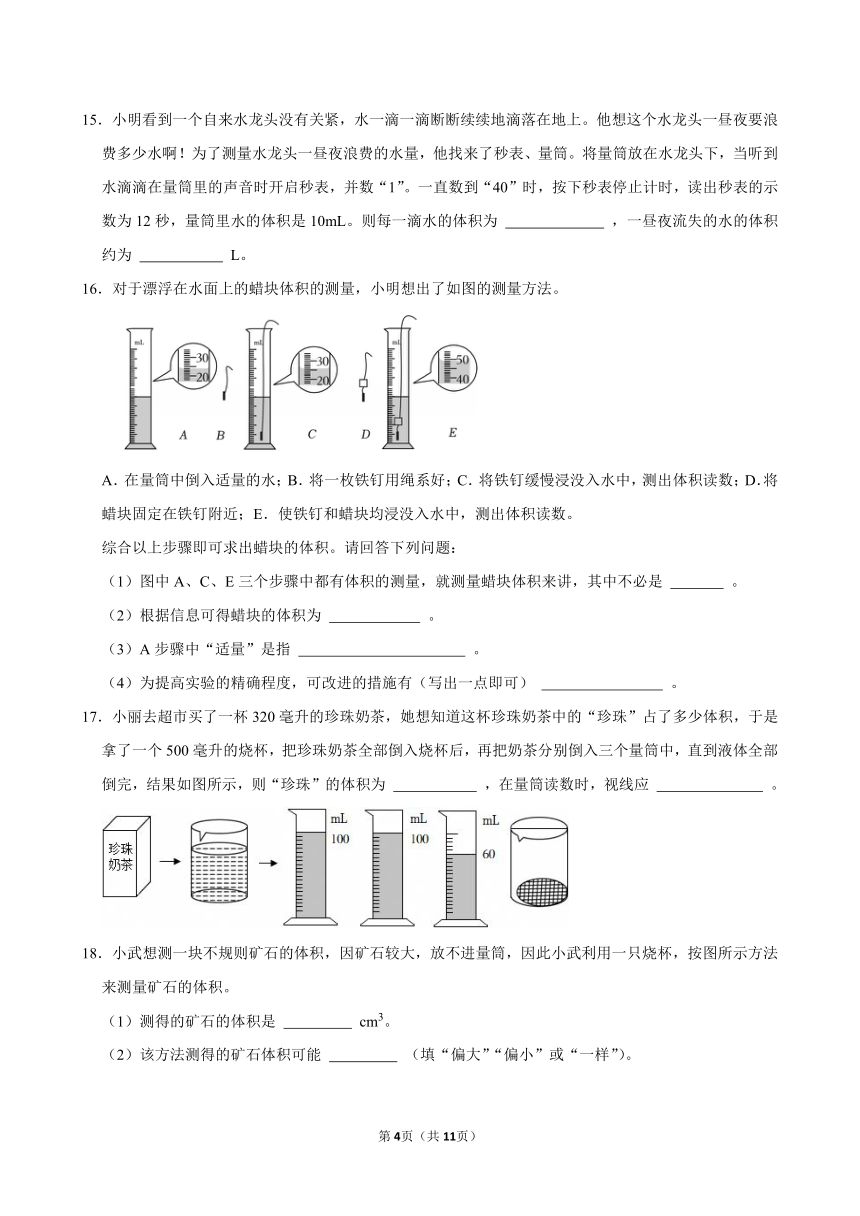
16.对于漂浮在水面上的蜡块体积的测量,小明想出了如图的测量方法。
A.在量筒中倒入适量的水;B.将一枚铁钉用绳系好;C.将铁钉缓慢浸没入水中,测出体积读数;D.将蜡块固定在铁钉附近;E.使铁钉和蜡块均浸没入水中,测出体积读数。
综合以上步骤即可求出蜡块的体积。请回答下列问题:
(1)图中A、C、E三个步骤中都有体积的测量,就测量蜡块体积来讲,其中不必是 。
(2)根据信息可得蜡块的体积为 。
(3)A步骤中“适量”是指 。
(4)为提高实验的精确程度,可改进的措施有(写出一点即可) 。
17.小丽去超市买了一杯320毫升的珍珠奶茶,她想知道这杯珍珠奶茶中的“珍珠”占了多少体积,于是拿了一个500毫升的烧杯,把珍珠奶茶全部倒入烧杯后,再把奶茶分别倒入三个量筒中,直到液体全部倒完,结果如图所示,则“珍珠”的体积为 ,在量筒读数时,视线应 。
18.小武想测一块不规则矿石的体积,因矿石较大,放不进量筒,因此小武利用一只烧杯,按图所示方法来测量矿石的体积。
(1)测得的矿石的体积是 cm3。
(2)该方法测得的矿石体积可能 (填“偏大”“偏小”或“一样”)。
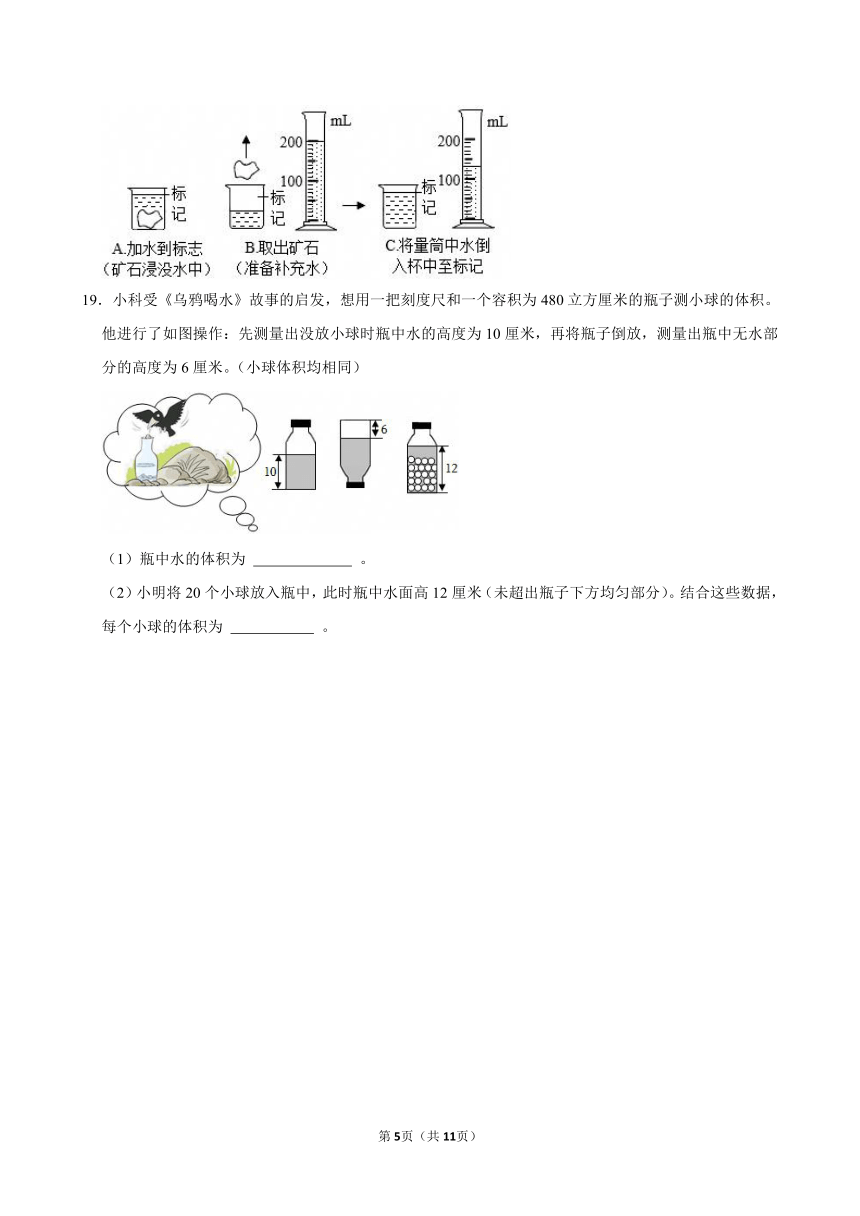
19.小科受《乌鸦喝水》故事的启发,想用一把刻度尺和一个容积为480立方厘米的瓶子测小球的体积。他进行了如图操作:先测量出没放小球时瓶中水的高度为10厘米,再将瓶子倒放,测量出瓶中无水部分的高度为6厘米。(小球体积均相同)
(1)瓶中水的体积为 。
(2)小明将20个小球放入瓶中,此时瓶中水面高12厘米(未超出瓶子下方均匀部分)。结合这些数据,每个小球的体积为 。
1.2科学测量(第二课时)同步练习
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D C C D C C D
一.选择题(共10小题)
1.【分析】测量物理量时,必须有一个共同的比较标准,标准不同测量结果不同。
【解答】解:阿凡提回答国王的提问时,选择不同的桶,得出的答案不同,但都是合理的,由此小故事我们可知:测量标准不同,测量结果也不同,为了科学地测量物理量需要确定大家公认的比较标准,测量前应该根据要求选择合适的测量工具。
故选:C。
2.【分析】根据量筒两次液面位置可以求出木块的一半体积,进而可得到木块的体积。
【解答】解:量筒内水的体积V1=40mL,当里面放入一木块,且木块的一半浸入水中时,量筒内液面的位置是V2=49mL,则一半木块的体积V=V2﹣V1=49mL﹣40mL=9cm3木块的体积是V=18cm3。
故选:D。
3.【分析】主要考查量筒的使用。
【解答】测量石块的体积,应用的是“排水法”。首先在量筒中倒入适量的水,记录数据;然后放入石块,记录数据。两次数据之差为石块的体积。所以顺序:①③④②
故答案为:A。
4.【分析】(1)观察一个大格分成几个小格,然后判断分度值。
(2)煤油的质量相等,密度相等,体积相等。
(3)量筒的分度值不同,分度值越小,测量越精确,误差越小。
【解答】解:A、甲量筒10ml和20ml之间分成5个小格,每一个小格代表2ml,1ml=1cm3,所以甲的分度值是2cm3,乙量筒10ml和20ml之间分成10个小格,每一个小格代表1ml,1ml=1cm3,所以乙的分度值是1cm3,故A错误。
B、煤油的质量相等,密度相等,体积相等,故B错误。
CD、甲的分度值是2ml,乙的分度值是1ml,乙的分度值小,精确度越高,误差越小,甲的分度值大,误差大,故C错误,D正确。
故选:D。
5.【分析】用量筒量取液体时,量筒要放平,读数时视线应与凹液面最低处相平;如果仰视液面,读数比实际偏低,若俯视液面,读数比实际偏大。根据量筒的读数与实际值的关系来判断该学生实际倒出液体的体积大小。
【解答】解:某同学用仰视的方法读得量筒内液体的体积为34毫升,其读数会比实际偏小,那么实际体积应大于34mL;倒出一部分液体后,再用俯视方法读得量筒内剩余液体体积为15毫升,其读数会比实际偏大,那么实际体积应小于15mL;则该学生实际倾倒的液体体积大于34mL﹣15mL=19mL。
故选:C。
6.【分析】因为石蜡的密度小于水的密度,可用悬重法测出石蜡的体积,即在石蜡下方系一铁块将石蜡坠入水中。
【解答】解:放入蜡块前,量筒的读数V2,放入蜡块后,量筒的读数为V3,蜡块的体积:V=V3﹣V2,故ABD错误,C正确。故选:C。
7.【分析】①量筒是测量液体体积的工具,被测液体体积不能超过量筒的最大测量值;
②要利用量筒和水测量石块的体积,必须使石块全部浸没在水中。
【解答】解:
石块形状不规则,不能利用刻度尺测量长度、宽度和高度,再计算体积,所以借助量筒和水,采用“排水法”测量其体积,为保证测量结果的准确,石块必须全部浸没在水中,同时石块放入水中后水面不超过量筒的最大测量值。
故选:D。
8.【分析】根据量筒的使用原理可知。
【解答】解:在体积一定的情况下,根据V=Sh可知,量筒的横截面积越小,h越大,相同体积的刻度间隔就越大,提高了测量的精度,同时便于读数,这是量筒做得细而高,不做成粗而矮的形状的原因。
故选:C。
9.【分析】本题考查使用量筒测量形状不规则固体体积的方法。对于密度大于水的固体而言使用方法一:先读出量筒中液体体积V1,然后将固体完全浸入水中,再读出量筒中水和固体的总体积V2,最后用总体积V2﹣V1得到固体体积V。对于密度小于水的密度的固体而言,由于它会漂浮在水面上无法下沉,我们要用到方法二,这种方法也叫“助沉法”。方法二:第一步先将密度大物体(如铁块)与待测物体用细线相连接,然后先将密度大的物体放入液体中读出体积V1,接下来将待测固体也放入液体中(保证两个物体完全浸没),读出此时体积V2,V2﹣V1即为待测固体体积。
【解答】利用助沉法测量形状不规则固体的体积首先测出水与助沉的铁块的总体积,即为图②中量筒中水和铁块总体积V2;接下来将待测物体及助沉的铁块一起浸没水中如图④所示,读出总体积V4,则待测物体体积为V4﹣V2。故选:C。
10.【分析】利用V=Sh求出水和水面上方空出部分的体积;瓶的容积等于水的容积和瓶中空出部分的体积之和。
【解答】解:图甲放置测得底面直径为D,底面积:S=π()2;
水的体积为:
V水=SH1=π()2×H1,
根据图乙可知,瓶中水面上方空出部分的体积:
V′=SH2=π()2×H2,
水瓶的容积:
V总=V水+V′=π()2×H1+π()2×H2πD2(H1+H2)。
故选:D。
二.填空题(共9小题)
11.【分析】(1)刻度尺读数时,首先是明确分度值,其次是明确物体的起始端和末端对应刻度尺的刻度值,再根据末端对应刻度值减去起始端所对刻度值即为物体长度,注意刻度尺要估读到分度值的下一位;
(2)量筒读数时视线应该与液面的凹面的底部相平。
【解答】解:(1)刻度尺上1cm之间有10个小格,所以一个小格代表1mm,即刻度尺的分度值为1mm;木块左侧与4.00cm刻线对齐,估读为4.00cm,右侧在7.7cm多一点的刻度上,估读为7.74cm,故木块的长度是:L=7.74cm﹣4.00cm=3.74cm;
(2)6mL到7mL之间有5小格,故分度值为0.2mL,又由于不需要估读,故读数为6.8mL;
故答案为:(1)3.74;(2)6.8。
12.【分析】由表盘上的单位可知测量的物理量是体积,根据表盘上面指针示数和表盘下的倍率读取体积数值。
【解答】解:由水表表盘上的单位m3可知测量的物理量的体积,根据各个表盘上的指针示数和表盘下的倍率可知水表的读数为242.44m3。
故答案为:体积;242.44。
13.【分析】物体放入量筒后,量筒内最低液面满足物体浸没时的水量为最少水量。
(1)根据浸没小石块时所需水的体积大小确定最少水量。
(2)在量筒中装入适量的水的标准是:①要能浸没物体;②浸没后的水面不能超过量筒的最大刻度。
【解答】解:(1)最少水量是指物体放入量筒后,量筒内最低液面满足浸没物体时的水量。
(2)利用100毫升的量筒,用排水法测出本题中体积为15厘米3小石块体积,95毫升的水放入石块后会超过量筒的量程(V总=95毫升+15厘米3=95毫升+15毫升=110毫升>100毫升),所以D不合适;5毫升、50毫升、80毫升的水都可能浸没体积为15厘米3小石块,且石块和水的总体积小于量筒的量程100毫升,故“适量的水”可能为5毫升、50毫升、80毫升,故选ABC。
故答案为:(1)石块能全部浸没;(2)ABC。
14.【分析】(1)最小刻度是相邻两刻度线之间的体积;用V=V2﹣V1计算石块的体积;
(2)根据量筒读数时的要求,视线要与量筒内液体凹液面的最低处保持水平,仰视读量筒内液体体积,读数比实际液体体积小;俯视读数比实际偏大;投入石块,有水滴飞溅出来,量筒的示数会变小;
【解答】解:(1)图中50mL到100mL之间有5个格,所以分度值是10mL;
石块的体积V=V2﹣V1=130mL﹣110mL=20mL=20cm3;
(2)A、量筒的示数与石块浸入水中深度无关,故A错误;
B、放入石块后,仰视读数,示数偏小,放入石块后与放入前的示数差就会变小,故B正确;
C、投入石块,有水滴飞溅出来,放入石块后的示数就变小了,放入石块后与放入前的示数差就会变小,故C正确;
D、改用粗线拴住石块,放入石块后与放入前的示数差就会变大,故D错误。
故选:BC;
故答案为:(1)10mL;20cm3;(2)BC。
15.【分析】从题可知,知道40滴水的总体积,从而可以计算出每一滴水的体积,知道12s内浪费水的体积,从而可以计算出1s内浪费水的体积,再计算出一昼夜浪费水的体积。
【解答】解:因为40滴水的体积是10mL,
所以一滴水的体积为:V0.25mL,
由于第一滴水滴后才开始计时,所以12s内滴落了应该是39滴,浪费的水滴体积应该为10mL﹣0.25mL=9.75mL。所以1s内浪费水的体积为:V00.8125mL,
则一昼夜浪费水的体积为:V总=V0×24×3600=0.8125mL×24×3600=70200mL≈70.2L。
故答案为:0.25mL;70.2。
16.【分析】A、往量筒中倒入适量的水,可读出水的体积V1;
C、将铁钉慢慢地浸没在量筒内的水中,此时量筒示数为V2;
E、将铁钉和蜡块慢慢的浸没在量筒内的水中,量筒读数为V3=49mL。
【解答】解:A、往量筒中倒入适量的水,可读出水的体积V1=24mL;
C、将铁钉慢慢地浸没在量筒内的水中,此时量筒示数为V2=26毫升;
E、将铁钉和蜡块慢慢的浸没在量筒内的水中,量筒读数为V3=49mL,则蜡块体积为:49mL﹣26mL=23mL=23cm3;
(1)测量水的体积是没有用的,故其中不必要读数的步骤是A;
(2)蜡块的体积为 23cm3;
(3)既要浸没,且浸没后不超过量筒的最大刻度;
(4)为提高实验的精确程度,可换分度值更小的量筒。
故答案为:(1)A; (2)23cm3; (3)既要浸没,且浸没后不超过量筒的最大刻度;(4)换分度值更小的量筒。
17.【分析】已知珍珠奶茶的总体积,由图知奶茶中液体的体积,两者的体积差就是珍珠的体积。
【解答】解:由图知,奶茶中液体的体积为100mL+100mL+60mL=260mL,奶茶的总体积为320mL,所以奶茶中珍珠的体积为320mL﹣260mL=60mL;在量筒读数时,视线应与液面底部相平。
故答案为:60mL;与液面底部相平。
18.【分析】(1)读量筒内液面对应的体积值时,视线应平视凹液面的最低处读数;
(2)将矿石从水中取出时,矿石表面沾有部分水。
【解答】解:量筒每100mL分10个小格,每小格10mL,即分度值是:10mL;C图中,量筒中水面与“130”对齐,所以剩余水的体积是130mL;B图中,量筒中水的体积是200mL,说明向烧杯中倒出了200mL﹣130mL=70mL水,所以矿石的体积是V=70mL=70cm3;由于将矿石从烧杯中拿出时,石块上会沾有水,所以测得的体积偏大。
故答案为:70cm3;偏大。
19.【分析】(1)根据瓶子空气体积不变,瓶子的容积可以看作是高度为10cm+6cm的圆柱的体积,而瓶子的容积为480立方厘米,据此得出截面积,瓶子中的水的高度为10厘米,得出瓶中水的体积;
(2)计算出瓶内的水上升的高度,计算瓶内水上升的水的体积就是20个小球的体积,由此求出20个小球的体积,再除以20求出每个小球的体积。
【解答】解:(1)根据瓶子空气体积不变,瓶子的容积可以看作是高度为10cm+6cm=16cm的圆柱的体积,
则瓶子的截面积S30cm2;
水的体积V'=Sh'=30cm2×10cm=300cm3;
(2)瓶中水面高12厘米时,上升的高度为Δh=12cm﹣10cm=2cm;
小球总体积:V总=SΔh=30cm2×2cm=60cm3;
每个小球的体积V13cm3。
故答案为:(1)300cm3;(2)3cm3。
第1页(共1页)
一.选择题(共10小题)
1.一次国王故意为难阿凡提,他在众臣面前一定要让阿凡提说出眼前池塘里的水有多少桶,阿凡提略加思索后回答:若桶像池塘一样大的话,池塘里的水就只有一桶;若桶只有池塘的十分之一大的话,池塘里的水就有十桶。这则故事说明了( )
A.测量总是有误差的
B.测量的准确程度由最小刻度决定
C.测量的标准不一样,结果也不一样
D.测量工具的量程决定了物体的大小
2.一个量筒中有40mL水,当里面放入一木块,且木块的一半浸入水中时,量筒的读数是49mL,则这块木块的体积是( )
A.8cm3 B.18mL C.18dm3 D.18cm3
3.在用量筒测石块体积的步骤中,正确序号排列为( )
①将适量水注入量筒中读出体积V2
②计算石块体积为V=V1﹣V2
③用细线系住石块放入量筒水中
④读出石块和水的总体积V1
A.①③④② B.④②③① C.③①④② D.③④①②
4.甲、乙两个量筒的分度值分别是2mL和1mL,用它们来测量等质量煤油的体积,如图所示。某同学的读数分别是13.8mL和13.9mL。则下列分析正确的是( )
A.甲量筒的分度值是1cm3
B.两次读数不同是因为煤油体积不同
C.两量筒的分度值不同,不影响误差大小
D.乙量筒的分度值小,因此精确度更高
5.某同学在用量筒量取液体时,先用仰视读得液体体积为34毫升,倒出一部分液体后,再用俯视读得液体体积为15毫升,则倒出的液体体积是( )
A.等于19mL B.小于19mL C.大于19mL D.无法判断
6.实验室在测固体密度时,需用量筒测出固体的体积,如果固体的密度小于水,而不能在水中下沉,我们常用如图的方法即“沉坠法”测出它的体积。如图所示是用量筒测量蜡块体积的过程,则蜡块的体积为(V1、V2、V3为当前水和物体的总体积)( )
A.V3﹣V1 B.V3﹣V2﹣V1 C.V3﹣V2 D.V2﹣V1
7.用量筒和水测小石块体积时,先在量筒内注入适量的水。“适量”的标准是( )
A.看上去不多也不少
B.能淹没石块,且石块放入水中后水不会溢出
C.水面约在量筒中间
D.能淹没石块,且石块放入水中后水不超过量程
8.量筒做得细而高,不做成粗而矮的形状,主要原因是( )
A.细高的量筒便于操作
B.细高的量筒可以做出相对较大的底座,增加稳度
C.细高的量筒与粗矮的量筒相比,相应的刻度间隔较大,能较准确地读数
D.粗矮量筒中的液体较多,筒壁所受压力较大,需用较厚的玻璃,因而不便读数
9.在量筒中注入适量的水,读出水面所对应的刻度值V1如图①所示;将铁块放入量筒中水面所对应的刻度值V2如图②所示;取出铁块,再将物块轻轻地放入水中,静止时如图③所示,水面所对应的刻度值为V3;将铁块和物块系在一起放入量筒中如图④所示,水面所对应的刻度值为V4。则物块的体积V的大小应该是( )
A.V2﹣V1 B.V3﹣V1 C.V4﹣V2 D.V4﹣V3
10.某注射用蒸馏水瓶,按图甲放置测得底面直径为D,液面高度为H1;按图乙放置,测得空间的高度为H2。若瓶子厚度不计,那么该瓶的容积为多大( )
A.DH1H2
B.D2(H1+H2)
C.
D.
二.填空题(共9小题)
11.(1)如图甲所示,木块的测量值是 cm。
(2)用10mL量筒量取液体如图乙所示,则液体的体积为 mL。
12.如图所示为家用自来水表的表盘,其测量的物理量是 ,其读数为 。
13.实验室用排水法测量形状不规则的小石块体积时,老师总是强调先要在量筒中加入“适量的水”。
(1)“适量”是指能用排水法测量出小石块体积的水量范围,其中最多水量是指小石块放入量筒后,会使液面上升到最大刻度线处的水量;最少水量是指小石块放入量筒后,量筒内的液面满足 的水量。
(2)现有100毫升的量筒,用排水法测出体积为15立方厘米的形状不规则的小石块,需加入“适量的水”的体积合适是 。
A.5毫升 B.50毫升 C.80毫升 D.95毫升
14.用量筒测量小石块的体积。甲同学的做法是:在量筒里注入适量的水,记下水的体积V1,然后轻轻放入石块,使量筒里的水完全浸没石块,记下此时水及石块的体积V2,计算石块的体积为V2﹣V1。
(1)如图所示,甲同学所用量筒的最小刻度是 ,小石块的体积是 。
(2)甲同学下列操作,可导致测量结果偏小的是 。
A.石块浸入水中深度过大
B.放入石块后,仰视读数
C.投入石块,有水滴飞溅出来
D.改用粗线拴住石块
15.小明看到一个自来水龙头没有关紧,水一滴一滴断断续续地滴落在地上。他想这个水龙头一昼夜要浪费多少水啊!为了测量水龙头一昼夜浪费的水量,他找来了秒表、量筒。将量筒放在水龙头下,当听到水滴滴在量筒里的声音时开启秒表,并数“1”。一直数到“40”时,按下秒表停止计时,读出秒表的示数为12秒,量筒里水的体积是10mL。则每一滴水的体积为 ,一昼夜流失的水的体积约为 L。
16.对于漂浮在水面上的蜡块体积的测量,小明想出了如图的测量方法。
A.在量筒中倒入适量的水;B.将一枚铁钉用绳系好;C.将铁钉缓慢浸没入水中,测出体积读数;D.将蜡块固定在铁钉附近;E.使铁钉和蜡块均浸没入水中,测出体积读数。
综合以上步骤即可求出蜡块的体积。请回答下列问题:
(1)图中A、C、E三个步骤中都有体积的测量,就测量蜡块体积来讲,其中不必是 。
(2)根据信息可得蜡块的体积为 。
(3)A步骤中“适量”是指 。
(4)为提高实验的精确程度,可改进的措施有(写出一点即可) 。
17.小丽去超市买了一杯320毫升的珍珠奶茶,她想知道这杯珍珠奶茶中的“珍珠”占了多少体积,于是拿了一个500毫升的烧杯,把珍珠奶茶全部倒入烧杯后,再把奶茶分别倒入三个量筒中,直到液体全部倒完,结果如图所示,则“珍珠”的体积为 ,在量筒读数时,视线应 。
18.小武想测一块不规则矿石的体积,因矿石较大,放不进量筒,因此小武利用一只烧杯,按图所示方法来测量矿石的体积。
(1)测得的矿石的体积是 cm3。
(2)该方法测得的矿石体积可能 (填“偏大”“偏小”或“一样”)。
19.小科受《乌鸦喝水》故事的启发,想用一把刻度尺和一个容积为480立方厘米的瓶子测小球的体积。他进行了如图操作:先测量出没放小球时瓶中水的高度为10厘米,再将瓶子倒放,测量出瓶中无水部分的高度为6厘米。(小球体积均相同)
(1)瓶中水的体积为 。
(2)小明将20个小球放入瓶中,此时瓶中水面高12厘米(未超出瓶子下方均匀部分)。结合这些数据,每个小球的体积为 。
1.2科学测量(第二课时)同步练习
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A D C C D C C D
一.选择题(共10小题)
1.【分析】测量物理量时,必须有一个共同的比较标准,标准不同测量结果不同。
【解答】解:阿凡提回答国王的提问时,选择不同的桶,得出的答案不同,但都是合理的,由此小故事我们可知:测量标准不同,测量结果也不同,为了科学地测量物理量需要确定大家公认的比较标准,测量前应该根据要求选择合适的测量工具。
故选:C。
2.【分析】根据量筒两次液面位置可以求出木块的一半体积,进而可得到木块的体积。
【解答】解:量筒内水的体积V1=40mL,当里面放入一木块,且木块的一半浸入水中时,量筒内液面的位置是V2=49mL,则一半木块的体积V=V2﹣V1=49mL﹣40mL=9cm3木块的体积是V=18cm3。
故选:D。
3.【分析】主要考查量筒的使用。
【解答】测量石块的体积,应用的是“排水法”。首先在量筒中倒入适量的水,记录数据;然后放入石块,记录数据。两次数据之差为石块的体积。所以顺序:①③④②
故答案为:A。
4.【分析】(1)观察一个大格分成几个小格,然后判断分度值。
(2)煤油的质量相等,密度相等,体积相等。
(3)量筒的分度值不同,分度值越小,测量越精确,误差越小。
【解答】解:A、甲量筒10ml和20ml之间分成5个小格,每一个小格代表2ml,1ml=1cm3,所以甲的分度值是2cm3,乙量筒10ml和20ml之间分成10个小格,每一个小格代表1ml,1ml=1cm3,所以乙的分度值是1cm3,故A错误。
B、煤油的质量相等,密度相等,体积相等,故B错误。
CD、甲的分度值是2ml,乙的分度值是1ml,乙的分度值小,精确度越高,误差越小,甲的分度值大,误差大,故C错误,D正确。
故选:D。
5.【分析】用量筒量取液体时,量筒要放平,读数时视线应与凹液面最低处相平;如果仰视液面,读数比实际偏低,若俯视液面,读数比实际偏大。根据量筒的读数与实际值的关系来判断该学生实际倒出液体的体积大小。
【解答】解:某同学用仰视的方法读得量筒内液体的体积为34毫升,其读数会比实际偏小,那么实际体积应大于34mL;倒出一部分液体后,再用俯视方法读得量筒内剩余液体体积为15毫升,其读数会比实际偏大,那么实际体积应小于15mL;则该学生实际倾倒的液体体积大于34mL﹣15mL=19mL。
故选:C。
6.【分析】因为石蜡的密度小于水的密度,可用悬重法测出石蜡的体积,即在石蜡下方系一铁块将石蜡坠入水中。
【解答】解:放入蜡块前,量筒的读数V2,放入蜡块后,量筒的读数为V3,蜡块的体积:V=V3﹣V2,故ABD错误,C正确。故选:C。
7.【分析】①量筒是测量液体体积的工具,被测液体体积不能超过量筒的最大测量值;
②要利用量筒和水测量石块的体积,必须使石块全部浸没在水中。
【解答】解:
石块形状不规则,不能利用刻度尺测量长度、宽度和高度,再计算体积,所以借助量筒和水,采用“排水法”测量其体积,为保证测量结果的准确,石块必须全部浸没在水中,同时石块放入水中后水面不超过量筒的最大测量值。
故选:D。
8.【分析】根据量筒的使用原理可知。
【解答】解:在体积一定的情况下,根据V=Sh可知,量筒的横截面积越小,h越大,相同体积的刻度间隔就越大,提高了测量的精度,同时便于读数,这是量筒做得细而高,不做成粗而矮的形状的原因。
故选:C。
9.【分析】本题考查使用量筒测量形状不规则固体体积的方法。对于密度大于水的固体而言使用方法一:先读出量筒中液体体积V1,然后将固体完全浸入水中,再读出量筒中水和固体的总体积V2,最后用总体积V2﹣V1得到固体体积V。对于密度小于水的密度的固体而言,由于它会漂浮在水面上无法下沉,我们要用到方法二,这种方法也叫“助沉法”。方法二:第一步先将密度大物体(如铁块)与待测物体用细线相连接,然后先将密度大的物体放入液体中读出体积V1,接下来将待测固体也放入液体中(保证两个物体完全浸没),读出此时体积V2,V2﹣V1即为待测固体体积。
【解答】利用助沉法测量形状不规则固体的体积首先测出水与助沉的铁块的总体积,即为图②中量筒中水和铁块总体积V2;接下来将待测物体及助沉的铁块一起浸没水中如图④所示,读出总体积V4,则待测物体体积为V4﹣V2。故选:C。
10.【分析】利用V=Sh求出水和水面上方空出部分的体积;瓶的容积等于水的容积和瓶中空出部分的体积之和。
【解答】解:图甲放置测得底面直径为D,底面积:S=π()2;
水的体积为:
V水=SH1=π()2×H1,
根据图乙可知,瓶中水面上方空出部分的体积:
V′=SH2=π()2×H2,
水瓶的容积:
V总=V水+V′=π()2×H1+π()2×H2πD2(H1+H2)。
故选:D。
二.填空题(共9小题)
11.【分析】(1)刻度尺读数时,首先是明确分度值,其次是明确物体的起始端和末端对应刻度尺的刻度值,再根据末端对应刻度值减去起始端所对刻度值即为物体长度,注意刻度尺要估读到分度值的下一位;
(2)量筒读数时视线应该与液面的凹面的底部相平。
【解答】解:(1)刻度尺上1cm之间有10个小格,所以一个小格代表1mm,即刻度尺的分度值为1mm;木块左侧与4.00cm刻线对齐,估读为4.00cm,右侧在7.7cm多一点的刻度上,估读为7.74cm,故木块的长度是:L=7.74cm﹣4.00cm=3.74cm;
(2)6mL到7mL之间有5小格,故分度值为0.2mL,又由于不需要估读,故读数为6.8mL;
故答案为:(1)3.74;(2)6.8。
12.【分析】由表盘上的单位可知测量的物理量是体积,根据表盘上面指针示数和表盘下的倍率读取体积数值。
【解答】解:由水表表盘上的单位m3可知测量的物理量的体积,根据各个表盘上的指针示数和表盘下的倍率可知水表的读数为242.44m3。
故答案为:体积;242.44。
13.【分析】物体放入量筒后,量筒内最低液面满足物体浸没时的水量为最少水量。
(1)根据浸没小石块时所需水的体积大小确定最少水量。
(2)在量筒中装入适量的水的标准是:①要能浸没物体;②浸没后的水面不能超过量筒的最大刻度。
【解答】解:(1)最少水量是指物体放入量筒后,量筒内最低液面满足浸没物体时的水量。
(2)利用100毫升的量筒,用排水法测出本题中体积为15厘米3小石块体积,95毫升的水放入石块后会超过量筒的量程(V总=95毫升+15厘米3=95毫升+15毫升=110毫升>100毫升),所以D不合适;5毫升、50毫升、80毫升的水都可能浸没体积为15厘米3小石块,且石块和水的总体积小于量筒的量程100毫升,故“适量的水”可能为5毫升、50毫升、80毫升,故选ABC。
故答案为:(1)石块能全部浸没;(2)ABC。
14.【分析】(1)最小刻度是相邻两刻度线之间的体积;用V=V2﹣V1计算石块的体积;
(2)根据量筒读数时的要求,视线要与量筒内液体凹液面的最低处保持水平,仰视读量筒内液体体积,读数比实际液体体积小;俯视读数比实际偏大;投入石块,有水滴飞溅出来,量筒的示数会变小;
【解答】解:(1)图中50mL到100mL之间有5个格,所以分度值是10mL;
石块的体积V=V2﹣V1=130mL﹣110mL=20mL=20cm3;
(2)A、量筒的示数与石块浸入水中深度无关,故A错误;
B、放入石块后,仰视读数,示数偏小,放入石块后与放入前的示数差就会变小,故B正确;
C、投入石块,有水滴飞溅出来,放入石块后的示数就变小了,放入石块后与放入前的示数差就会变小,故C正确;
D、改用粗线拴住石块,放入石块后与放入前的示数差就会变大,故D错误。
故选:BC;
故答案为:(1)10mL;20cm3;(2)BC。
15.【分析】从题可知,知道40滴水的总体积,从而可以计算出每一滴水的体积,知道12s内浪费水的体积,从而可以计算出1s内浪费水的体积,再计算出一昼夜浪费水的体积。
【解答】解:因为40滴水的体积是10mL,
所以一滴水的体积为:V0.25mL,
由于第一滴水滴后才开始计时,所以12s内滴落了应该是39滴,浪费的水滴体积应该为10mL﹣0.25mL=9.75mL。所以1s内浪费水的体积为:V00.8125mL,
则一昼夜浪费水的体积为:V总=V0×24×3600=0.8125mL×24×3600=70200mL≈70.2L。
故答案为:0.25mL;70.2。
16.【分析】A、往量筒中倒入适量的水,可读出水的体积V1;
C、将铁钉慢慢地浸没在量筒内的水中,此时量筒示数为V2;
E、将铁钉和蜡块慢慢的浸没在量筒内的水中,量筒读数为V3=49mL。
【解答】解:A、往量筒中倒入适量的水,可读出水的体积V1=24mL;
C、将铁钉慢慢地浸没在量筒内的水中,此时量筒示数为V2=26毫升;
E、将铁钉和蜡块慢慢的浸没在量筒内的水中,量筒读数为V3=49mL,则蜡块体积为:49mL﹣26mL=23mL=23cm3;
(1)测量水的体积是没有用的,故其中不必要读数的步骤是A;
(2)蜡块的体积为 23cm3;
(3)既要浸没,且浸没后不超过量筒的最大刻度;
(4)为提高实验的精确程度,可换分度值更小的量筒。
故答案为:(1)A; (2)23cm3; (3)既要浸没,且浸没后不超过量筒的最大刻度;(4)换分度值更小的量筒。
17.【分析】已知珍珠奶茶的总体积,由图知奶茶中液体的体积,两者的体积差就是珍珠的体积。
【解答】解:由图知,奶茶中液体的体积为100mL+100mL+60mL=260mL,奶茶的总体积为320mL,所以奶茶中珍珠的体积为320mL﹣260mL=60mL;在量筒读数时,视线应与液面底部相平。
故答案为:60mL;与液面底部相平。
18.【分析】(1)读量筒内液面对应的体积值时,视线应平视凹液面的最低处读数;
(2)将矿石从水中取出时,矿石表面沾有部分水。
【解答】解:量筒每100mL分10个小格,每小格10mL,即分度值是:10mL;C图中,量筒中水面与“130”对齐,所以剩余水的体积是130mL;B图中,量筒中水的体积是200mL,说明向烧杯中倒出了200mL﹣130mL=70mL水,所以矿石的体积是V=70mL=70cm3;由于将矿石从烧杯中拿出时,石块上会沾有水,所以测得的体积偏大。
故答案为:70cm3;偏大。
19.【分析】(1)根据瓶子空气体积不变,瓶子的容积可以看作是高度为10cm+6cm的圆柱的体积,而瓶子的容积为480立方厘米,据此得出截面积,瓶子中的水的高度为10厘米,得出瓶中水的体积;
(2)计算出瓶内的水上升的高度,计算瓶内水上升的水的体积就是20个小球的体积,由此求出20个小球的体积,再除以20求出每个小球的体积。
【解答】解:(1)根据瓶子空气体积不变,瓶子的容积可以看作是高度为10cm+6cm=16cm的圆柱的体积,
则瓶子的截面积S30cm2;
水的体积V'=Sh'=30cm2×10cm=300cm3;
(2)瓶中水面高12厘米时,上升的高度为Δh=12cm﹣10cm=2cm;
小球总体积:V总=SΔh=30cm2×2cm=60cm3;
每个小球的体积V13cm3。
故答案为:(1)300cm3;(2)3cm3。
第1页(共1页)
同课章节目录
