(2)数与式(含解析)——初升高数学人教A版(2019)教材衔接
文档属性
| 名称 | (2)数与式(含解析)——初升高数学人教A版(2019)教材衔接 |  | |
| 格式 | docx | ||
| 文件大小 | 665.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 14:39:19 | ||
图片预览




文档简介
(2)数与式——初升高数学人教A版(2019)教材衔接
回顾初中
1.乘法公式
平方差公式:
完全平方公式:
2.因式分解
系数为1的十字相乘法分解因式:
3.分式与根式
分式的意义:形如的式子,若中含有字母,且,则称为分式.
分式的基本性质:当时,,.
二次根式:式子叫做二次根式.
衔接高中
1.乘法公式
立方和公式:
立方差公式:
2.因式分解
系数不为1的十字相乘法分解因式:对于二次三项式,如果二次项系数可以分解成两个因数之积,即,常数项可以分解成两个因数之积,即,那么排列如图所示
将与按斜线交叉相乘,再相加,得到,若它正好等于二次三项式的一次项系数,即,则二次三项式就可以分解为两个因式与之积,即.
像这种借助画十字交叉线分解系数,从而帮助我们把二次三项式分解因式的方法,叫做十字相乘法
3.分式与根式
像这样,分子或分母中又含有分式的分式叫做繁分式
一般地,与,与,与互为有理化因式
习题衔接
1.如果,则m的值为( )
A.6 B.8 C.-8 D.-6
2.已知,则( )
A.12 B.14 C.8 D.16
3.已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘为,乙与丙相乘为,则甲与丙相加的结果为( )
A. B. C. D.
4.若能分解成两个一次因式的积,则m的值为( )
A.1 B. C. D.2
5.已知,,则代数式的值为( )
A.9 B. C.3 D.5
6.如图,将正方形和正方形放置在较大的正方形中,重叠部分是一个较小的正方形,其面积为1,已知,,则空白部分的面积为( )
A. B. C. D.
7.已知实数a,b满足,则下列判断正确的是( )
A. B.
C. D.
8.当,时,的值为( )
A.1 B. C. D.4
9.设,,,则a、b、c之间的大小关系是( )
A. B. C. D.
10.已知,,,…,(n为正整数,且,),则用含t的式子的结果为( )
A.t B. C. D.
11.计算:________.
12.对于二次三项式,如果能将常数项n分解成两个因数a,b,使a,b的和恰好等于一次项系数m,即,,就能将分解因式.这种分解因式的方法取名为“十字相乘法”.为使分解过程直观,常常采用图示的方法,将二次项系数与常数项的因数分成两列(如图),再交叉相乘并求和,检验是否等于一次项系数,进而进行因式分解.则代数式因式分解的结果为______.
13.阅读理解对于任意正整数a,b,∵,∴,∴,只有当时,等号成立;结论:在(a、b均为正实数)中,只有当时,有最小值.若,有最小值为______.
14.甲、乙两个同学分解因式时,甲看错了m,分解结果为;乙看错了n,分解结果为,则正确的分解结果为____________.
15.(1)【阅读与思考】
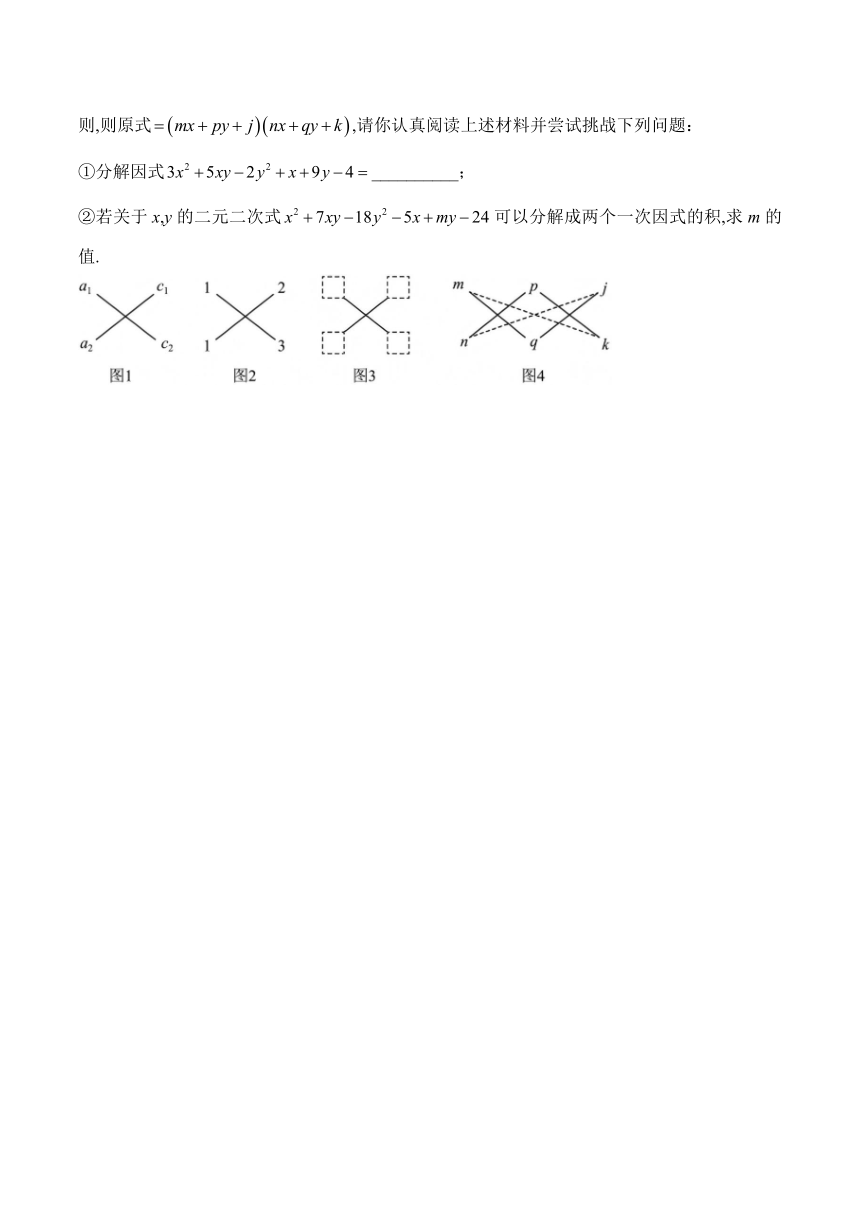
整式乘法与因式分解是方向相反的变形.如何把二次三项式分解因式呢?我们已经知道:.反过来,就得到:.我们发现,二次三项式的二次项的系数a分解成,常数项c分解成,并且把,,,,如图1所示摆放,按对角线交叉相乘再相加,就得到,如果的值正好等于的一次项系数b,那么就可以分解为,其中,位于图的上一行,,位于下一行.像这种借助画十字交叉图分解系数,从而帮助我们把二次三项式分解因式的方法,通常叫做“十字相乘法”.
例如,将式子分解因式的具体步骤为:首先把二次项的系数1分解为两个因数的积,即,把常数项也分解为两个因数的积,即;然后把1,1,2,按图2所示的摆放,按对角线交叉相乘再相加的方法,得到,恰好等于一次项的系数,于是就可以分解为.
请同学们认真观察和思考,尝试在图3的虚线方框内填入适当的数,并用“十字相乘法”分解因式:__________.
(2)【理解与应用】
请你仔细体会上述方法并尝试对下面两个二次三项式进行分解因式:
①__________;
②__________.
(3)【探究与拓展】
对于形如的关于x,y的二元二次多项式也可以用“十字相乘法”来分解,如图4.将a分解成乘积作为一列,c分解成乘积作为第二列,f分解成乘积作为第三列,如果,,,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式,请你认真阅读上述材料并尝试挑战下列问题:
①分解因式__________;
②若关于x,y的二元二次式可以分解成两个一次因式的积,求m的值.
答案以及解析
1.答案:D
解析:∵,
∴.
故选:D.
2.答案:B
解析:,
,
,
,
故选:B.
3.答案:A
解析:∵
∴甲为:,乙为:,丙为:,
∴, 故选A.
4.答案:C
解析:原式
故,,,
解得:,,或,,,
.
故选C.
5.答案:C
解析:∵,,
∴,,
∴,
故选:C.
6.答案:A
解析:正方形和正方形的面积分别为,,
正方形和正方形的边长分别为3,,
重叠部分是一个较小的正方形,其面积为1,
重叠部分的正方形边长为1,
大的正方形边长为,
空白部分的面积为,
故选:A.
7.答案:C
解析:由可得,
,
,
,
即对所有成立.
将代入得:
,
,
,
即对所有成立.
故选:C.
8.答案:C
解析:
,
,
当,时,
,,,
原式,
故选;C.
9.答案:D
解析:,
.
,
.
,
,
.
故选D.
10.答案:A
解析:由题意可得,
,
,
,
,
,
由上可得,上面的数据,每三个为一个循环,
,,
,
故选:A.
11.答案:
解析:原式,
,
,
故答案为:.
12.答案:
解析:
.
故答案为:.
13.答案:4
解析:由题中结论可得
,
即:当时,有最小值为4,
故答案为:4.
14.答案:
解析:甲看错了m,分解结果为,
由,可知,
又乙看错了n,分解结果为,
由,可知,
,
,
正确的分解结果为.
故答案为:.
15.答案:(1)
(2);
(3);43或
解析:(1)首先把二次项的系数1分解为两个因数的积,即,把常数项也分解为两个因数的积,即,所以.
故答案为:.
(2)①把二次项系数2写成,,满足,所以.
故答案为:.
②把项系数6写成,把项系数2写成,满足,
所以.
故答案为:.
(3)①把项系数3写成,把项系数-2写成,常数项-4写成满足条件,
所以.
故答案为:.
②把项系数1写成,把项系数-18写成,常数项-24写成或满足条件,
所以或,
故m的值为43或-78.
回顾初中
1.乘法公式
平方差公式:
完全平方公式:
2.因式分解
系数为1的十字相乘法分解因式:
3.分式与根式
分式的意义:形如的式子,若中含有字母,且,则称为分式.
分式的基本性质:当时,,.
二次根式:式子叫做二次根式.
衔接高中
1.乘法公式
立方和公式:
立方差公式:
2.因式分解
系数不为1的十字相乘法分解因式:对于二次三项式,如果二次项系数可以分解成两个因数之积,即,常数项可以分解成两个因数之积,即,那么排列如图所示
将与按斜线交叉相乘,再相加,得到,若它正好等于二次三项式的一次项系数,即,则二次三项式就可以分解为两个因式与之积,即.
像这种借助画十字交叉线分解系数,从而帮助我们把二次三项式分解因式的方法,叫做十字相乘法
3.分式与根式
像这样,分子或分母中又含有分式的分式叫做繁分式
一般地,与,与,与互为有理化因式
习题衔接
1.如果,则m的值为( )
A.6 B.8 C.-8 D.-6
2.已知,则( )
A.12 B.14 C.8 D.16
3.已知甲、乙、丙均为x的一次多项式,且其一次项的系数皆为正整数.若甲与乙相乘为,乙与丙相乘为,则甲与丙相加的结果为( )
A. B. C. D.
4.若能分解成两个一次因式的积,则m的值为( )
A.1 B. C. D.2
5.已知,,则代数式的值为( )
A.9 B. C.3 D.5
6.如图,将正方形和正方形放置在较大的正方形中,重叠部分是一个较小的正方形,其面积为1,已知,,则空白部分的面积为( )
A. B. C. D.
7.已知实数a,b满足,则下列判断正确的是( )
A. B.
C. D.
8.当,时,的值为( )
A.1 B. C. D.4
9.设,,,则a、b、c之间的大小关系是( )
A. B. C. D.
10.已知,,,…,(n为正整数,且,),则用含t的式子的结果为( )
A.t B. C. D.
11.计算:________.
12.对于二次三项式,如果能将常数项n分解成两个因数a,b,使a,b的和恰好等于一次项系数m,即,,就能将分解因式.这种分解因式的方法取名为“十字相乘法”.为使分解过程直观,常常采用图示的方法,将二次项系数与常数项的因数分成两列(如图),再交叉相乘并求和,检验是否等于一次项系数,进而进行因式分解.则代数式因式分解的结果为______.
13.阅读理解对于任意正整数a,b,∵,∴,∴,只有当时,等号成立;结论:在(a、b均为正实数)中,只有当时,有最小值.若,有最小值为______.
14.甲、乙两个同学分解因式时,甲看错了m,分解结果为;乙看错了n,分解结果为,则正确的分解结果为____________.
15.(1)【阅读与思考】
整式乘法与因式分解是方向相反的变形.如何把二次三项式分解因式呢?我们已经知道:.反过来,就得到:.我们发现,二次三项式的二次项的系数a分解成,常数项c分解成,并且把,,,,如图1所示摆放,按对角线交叉相乘再相加,就得到,如果的值正好等于的一次项系数b,那么就可以分解为,其中,位于图的上一行,,位于下一行.像这种借助画十字交叉图分解系数,从而帮助我们把二次三项式分解因式的方法,通常叫做“十字相乘法”.
例如,将式子分解因式的具体步骤为:首先把二次项的系数1分解为两个因数的积,即,把常数项也分解为两个因数的积,即;然后把1,1,2,按图2所示的摆放,按对角线交叉相乘再相加的方法,得到,恰好等于一次项的系数,于是就可以分解为.
请同学们认真观察和思考,尝试在图3的虚线方框内填入适当的数,并用“十字相乘法”分解因式:__________.
(2)【理解与应用】
请你仔细体会上述方法并尝试对下面两个二次三项式进行分解因式:
①__________;
②__________.
(3)【探究与拓展】
对于形如的关于x,y的二元二次多项式也可以用“十字相乘法”来分解,如图4.将a分解成乘积作为一列,c分解成乘积作为第二列,f分解成乘积作为第三列,如果,,,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式,请你认真阅读上述材料并尝试挑战下列问题:
①分解因式__________;
②若关于x,y的二元二次式可以分解成两个一次因式的积,求m的值.
答案以及解析
1.答案:D
解析:∵,
∴.
故选:D.
2.答案:B
解析:,
,
,
,
故选:B.
3.答案:A
解析:∵
∴甲为:,乙为:,丙为:,
∴, 故选A.
4.答案:C
解析:原式
故,,,
解得:,,或,,,
.
故选C.
5.答案:C
解析:∵,,
∴,,
∴,
故选:C.
6.答案:A
解析:正方形和正方形的面积分别为,,
正方形和正方形的边长分别为3,,
重叠部分是一个较小的正方形,其面积为1,
重叠部分的正方形边长为1,
大的正方形边长为,
空白部分的面积为,
故选:A.
7.答案:C
解析:由可得,
,
,
,
即对所有成立.
将代入得:
,
,
,
即对所有成立.
故选:C.
8.答案:C
解析:
,
,
当,时,
,,,
原式,
故选;C.
9.答案:D
解析:,
.
,
.
,
,
.
故选D.
10.答案:A
解析:由题意可得,
,
,
,
,
,
由上可得,上面的数据,每三个为一个循环,
,,
,
故选:A.
11.答案:
解析:原式,
,
,
故答案为:.
12.答案:
解析:
.
故答案为:.
13.答案:4
解析:由题中结论可得
,
即:当时,有最小值为4,
故答案为:4.
14.答案:
解析:甲看错了m,分解结果为,
由,可知,
又乙看错了n,分解结果为,
由,可知,
,
,
正确的分解结果为.
故答案为:.
15.答案:(1)
(2);
(3);43或
解析:(1)首先把二次项的系数1分解为两个因数的积,即,把常数项也分解为两个因数的积,即,所以.
故答案为:.
(2)①把二次项系数2写成,,满足,所以.
故答案为:.
②把项系数6写成,把项系数2写成,满足,
所以.
故答案为:.
(3)①把项系数3写成,把项系数-2写成,常数项-4写成满足条件,
所以.
故答案为:.
②把项系数1写成,把项系数-18写成,常数项-24写成或满足条件,
所以或,
故m的值为43或-78.
同课章节目录
