《高考快车道》2026版高三一轮总复习数学(基础版)79 第七章 阶段提能(十三) 空间向量及应用 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)79 第七章 阶段提能(十三) 空间向量及应用 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:02 | ||
图片预览









文档简介
(共36张PPT)
第七章 立体几何与空间向量
阶段提能(十三) 空间向量及应用
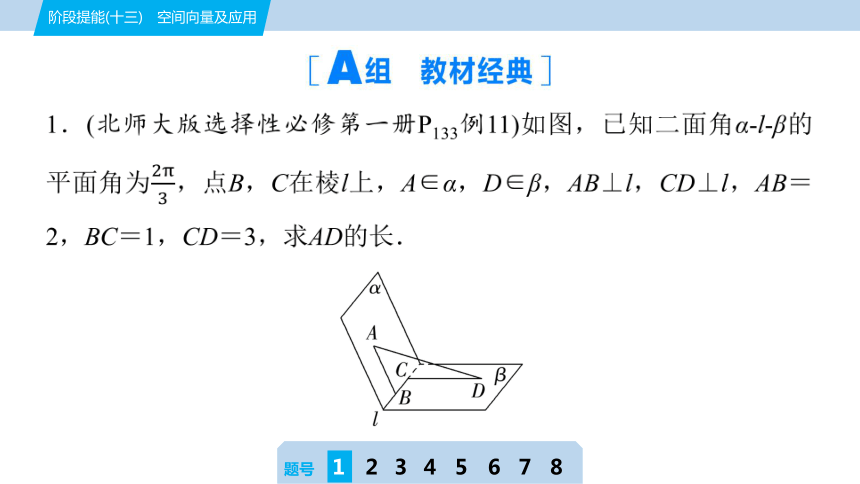
1.(北师大版选择性必修第一册P133例11)如图,已知二面角α-l-β的平面角为,点B,C在棱l上,A∈α,D∈β,AB⊥l,CD⊥l,AB=2,BC=1,CD=3,求AD的长.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
[解] 因为AB⊥l,CD⊥l,二面角α-l-β的平面角为,
所以·=0,·=0,〈〉=.
因为=,
所以||2=()·()
=||2+||2+||2+2·+2·+2·
=||2+||2+||2+2·
=22+12+32+2×2×3×=20.
所以|AD|=2.
题号
1
3
5
2
4
6
8
7
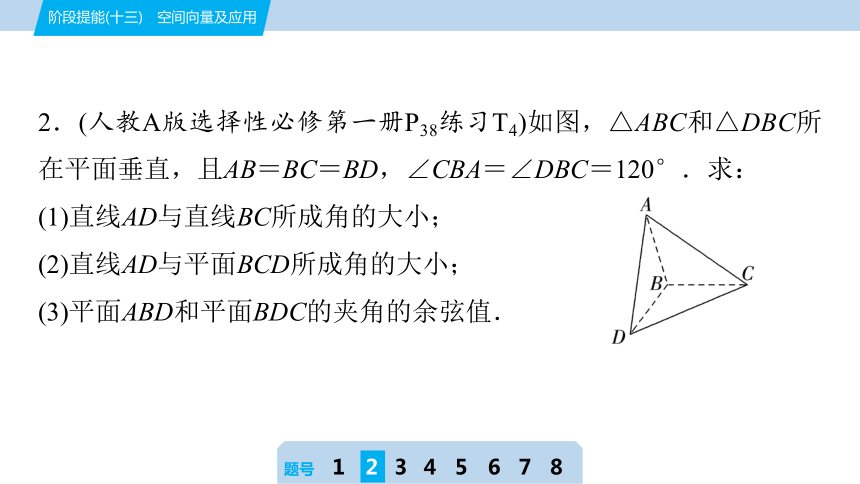
2.(人教A版选择性必修第一册P38练习T4)如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°.求:
(1)直线AD与直线BC所成角的大小;
(2)直线AD与平面BCD所成角的大小;
(3)平面ABD和平面BDC的夹角的余弦值.
题号
1
3
5
2
4
6
8
7
[解] 如图,建立空间直角坐标系.
设AB=a,则 A,
C(0,a,0),D,
∴=,
=(0,a,0),=.
(1)∵·=0,∴AD⊥BC,
∴直线AD与直线BC所成角的大小为90°.
(2)设AD与平面BCD所成的角为θ,
∵n=(0,0,1)是平面BCD的一个法向量,
∴sin θ=|cos 〈,n〉|===.
∴θ=45°,即直线AD与平面BCD所成角的大小为45°.
题号
1
3
5
2
4
6
8
7
(3)设m=(x,y,z)是平面ABD的法向量,
则∴
取x=1,则z=1,y=,∴m=(1,,1).
∴cos 〈m,n〉===.
设平面ABD和平面BDC的夹角为θ,则cos θ=|cos 〈m,n〉|=.
故平面ABD和平面BDC夹角的余弦值为.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
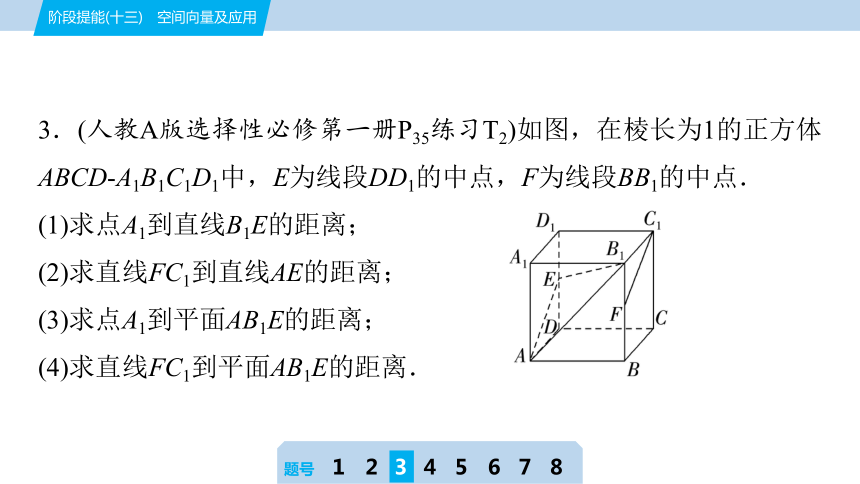
3.(人教A版选择性必修第一册P35练习T2)如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1)求点A1到直线B1E的距离;
(2)求直线FC1到直线AE的距离;
(3)求点A1到平面AB1E的距离;
(4)求直线FC1到平面AB1E的距离.
题号
1
3
5
2
4
6
8
7
[解] 建立如图所示的空间直角坐标系,则A1(1,0,1),B1(1,1,
1),E,F,C1(0,1,1),A(1,0,0).
(1)=,
u1===(0,1,0).
设a1==∴=1,a1·u1=-,
∴点A1到直线B1E的距离为==.
(2)∵==,
∴∴,
∴点F到直线AE的距离即为直线FC1到直线AE的距离.
u2===.
设a2==,∴=,a2·u2=.
∴直线FC1到直线AE的距离为=.
题号
1
3
5
2
4
6
8
7
(3)设平面AB1E的法向量为n=(x,y,z),
又=(0,1,1),=,
∴
取z=2,则y=-2,x=1,
∴n=(1,-2,2),∴n0==.
又=(0,0,1),∴点A1到平面AB1E的距离为|·n0|=.
题号
1
3
5
2
4
6
8
7
(4)∵FC1∥AE,FC1 平面AB1E,AE 平面AB1E,
∴FC1∥平面AB1E,
∴FC1到平面AB1E的距离即为F到平面AB1E的距离.
又平面AB1E的单位法向量n0==,
∴直线FC1到平面AB1E的距离为|·n0|=.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
4.(2024·上海卷)定义一个集合Ω,其元素是空间内的点,任取P1,P2,P3∈Ω,存在不全为0的实数λ1,λ2,λ3,使得λ1+λ2+λ3=0(其中O为坐标原点).已知(1,0,0)∈Ω,则(0,0,1) Ω的充分条件是( )
A.(0,0,0)∈Ω B.(-1,0,0)∈Ω
C.(0,1,0)∈Ω D.(0,0,-1)∈Ω
√
题号
1
3
5
2
4
6
8
7
C [由题意知这三个向量共面,即这三个向量不能构成空间的一个基底,
对A,由空间直角坐标系易知(0,0,0),(1,0,0),(0,0,1)三个向量共面,则当(0,0,0),(1,0,0)∈Ω无法推出(0,0,1) Ω,故A错误;
对B,由空间直角坐标系易知(-1,0,0),(1,0,0),(0,0,1)三个向量共面,则当(-1,0,0),(1,0,0)∈Ω无法推出(0,0,1) Ω,故B错误;
对C,由空间直角坐标系易知(1,0,0),(0,0,1),(0,1,0)三个向量不共面,可构成空间的一个基底,
则由(1,0,0),(0,1,0)∈Ω能推出(0,0,1) Ω,
对D,由空间直角坐标系易知(1,0,0),(0,0,1),(0,0,-1)三个向量共面,
则当(0,0,-1),(1,0,0)∈Ω无法推出(0,0,1) Ω,故D错误.故选C.]
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
5.(2024·全国甲卷)如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等腰梯形,BC∥AD,EF∥AD,AD=4,AB=BC=EF=2,ED=,FB=2,M为AD的中点.
(1)证明:BM∥平面CDE;
(2)求二面角F-BM-E的正弦值.
题号
1
3
5
2
4
6
8
7
[解] (1)证明:因为BC∥AD,BC=2,AD=4,M为AD的中点,所以BC∥MD,BC=MD,
所以四边形BCDM为平行四边形,所以BM∥CD,又因为BM 平面CDE,
CD 平面CDE,所以BM∥平面CDE.
(2)如图所示,作BO⊥AD交AD于点O,连接OF,
因为四边形ABCD为等腰梯形,BC∥AD,
AD=4,AB=BC=2,所以CD=2,
结合(1)四边形BCDM为平行四边形,
可得BM=CD=2,又AM=2,
所以△ABM为等边三角形,O为AM的中点,所以OB=.
又因为四边形ADEF为等腰梯形,M为AD中点,所以EF=MD,EF∥MD,
四边形EFMD为平行四边形,FM=ED=AF,
题号
1
3
5
2
4
6
8
7
所以△AFM为等腰三角形,△ABM与△AFM底边上中点O重合,OF⊥AM,OF==3.
又因为BF=2,则OB2+OF2=BF2,所以OB⊥OF,所以OB,OD,OF互相垂直,
以为x轴正方向,为y轴正方向,为z轴正方向,建立空间直角坐标系,
则F (0,0,3),B(,0,0),M(0,1,0),E(0,2,3),=
(-,1,0),=(-,0,3),
题号
1
3
5
2
4
6
8
7
=(-,2,3),设平面BFM的法向量为m=(x1,y1,z1),
则即
令x1=,得y1=3,z1=1,
即m=(,3,1)是平面BFM的一个法向量,
设平面EMB的法向量为n=(x2,y2,z2),
则即
题号
1
3
5
2
4
6
8
7
令x2=,得y2=3,z2=-1,
即n=(,3,-1)是平面EMB的一个法向量,
则cos 〈m,n〉===,
则sin 〈m,n〉=,
故二面角F-BM-E的正弦值为.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
6.(2023·新高考Ⅰ卷)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.
(1)证明:B2C2∥A2D2;
(2)点P在棱BB1上,当二面角P-A2C2-D2为150°时,
求B2P.
题号
1
3
5
2
4
6
8
7
[解] (1)证明:以点C为坐标原点,CD,CB,CC1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,则B2(0,2,2),C2(0,0,3),A2(2,2,1),D2(2,0,2),
所以=(0,-2,1),
=(0,-2,1),
所以=,所以B2C2∥A2D2.
(2)设BP=n(0≤n≤4),则P(0,2,n),
所以=(2,0,1-n),=(0,-2,3-n),
设平面PA2C2的法向量为a=(x1,y1,z1),
所以则
令x1=n-1,得a=(n-1,3-n,2).
设平面A2C2D2的法向量为b=(x2,y2,z2),
又=(-2,-2,2),=(0,-2,1),
题号
1
3
5
2
4
6
8
7
所以则
令y2=1,得b=(1,1,2).
所以|cos 150°|=|cos 〈a,b〉|
==,
整理得n2-4n+3=0,解得n=1或n=3,所以BP=1或BP=3,
所以B2P=1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
7.(2024·天津卷)如图,已知直四棱柱ABCD-A1B1C1D1中,AD⊥AB,AB∥CD,AA1=2,AB=2AD=2,DC=1,N是B1C1的中点,M是DD1的中点.
(1)求证:D1N∥平面CB1M;
(2)求平面CB1M与平面BB1C1C夹角的余弦值;
(3)求点B到平面CB1M的距离.
题号
1
3
5
2
4
6
8
7
[解] (1)证明:取CB1的中点P,连接NP,MP,
由N是B1C1的中点,故NP∥CC1,且NP=CC1,
由M是DD1的中点,故D1M=DD1=CC1,且D1M∥CC1,
则有D1M∥NP,D1M=NP,
故四边形D1MPN是平行四边形,故D1N∥MP.
又MP 平面CB1M,D1N 平面CB1M,
故D1N∥平面CB1M.
(2)由题意知,AA1,AB,AD两两垂直,以A为原点建立如图所示空间直角坐标系,
则A(0,0,0),B(2,0,0),B1(2,0,2),
M(0,1,1),C(1,1,0),C1(1,1,2),
则有=(1,-1,2),=(-1,0,1),
=(0,0,2).
设平面CB1M与平面BB1C1C的法向量分别为m=(x1,y1,z1),n=(x2,y2,z2),
题号
1
3
5
2
4
6
8
7
则有
分别取x1=x2=1,则有y1=3,
z1=1,y2=1,z2=0,即m=(1,3,1),n=(1,1,0),
设平面CB1M与平面BB1C1C的夹角为θ,
则cos θ=|cos 〈m,n〉|===,
故平面CB1M与平面BB1C1C夹角的余弦值为.
题号
1
3
5
2
4
6
8
7
(3)由=(0,0,2),平面CB1M的一个法向量m=(1,3,1),
则有==,
即点B到平面CB1M的距离为.
题号
1
3
5
2
4
6
8
7
8.(2022·新高考Ⅰ卷)如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面积为2 .
(1)求A到平面A1BC的距离;
(2)设D为A1C的中点,AA1=AB,平面A1BC⊥
平面ABB1A1,求二面角A-BD-C的正弦值.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
[解] (1)在直三棱柱ABC-A1B1C1中,设点A到平面A1BC的距离为h,
则=·h=h==·S△ABC·A1A==,
解得h=,
所以点A到平面A1BC的距离为.
(2)取A1B的中点E,连接AE,因为AA1=AB,所以AE⊥A1B,又平面A1BC⊥平面ABB1A1,平面A1BC∩平面ABB1A1=A1B,且AE 平面ABB1A1,所以AE⊥平面A1BC,在直三棱柱ABC - A1B1C1中,BB1⊥平面ABC,由BC 平面A1BC,BC 平面ABC,可得AE⊥BC,BB1⊥BC,又AE,BB1 平面ABB1A1且相交,所以BC⊥平面ABB1A1,所以BC,BA,BB1两两垂直,以B为原点,建立空间直角坐标系,如图,
题号
1
3
5
2
4
6
8
7
由(1)得AE=,所以AA1=AB=2,A1B=2 ,所以BC=2,
则A(0,2,0),A1(0,2,2),B(0,0,0),C(2,0,0),所以A1C的中点D(1,1,1),
则=(1,1,1),=(0,2,0),=(2,0,0).
设平面ABD的法向量m=(x,y,z),
则可取m=(1,0,-1),
题号
1
3
5
2
4
6
8
7
设平面BDC的法向量n=(a,b,c),
则可取n=(0,1,-1),
则cos 〈m,n〉===,
所以二面角A-BD-C的正弦值为=.
题号
1
3
5
2
4
6
8
7
谢 谢 !
第七章 立体几何与空间向量
阶段提能(十三) 空间向量及应用
1.(北师大版选择性必修第一册P133例11)如图,已知二面角α-l-β的平面角为,点B,C在棱l上,A∈α,D∈β,AB⊥l,CD⊥l,AB=2,BC=1,CD=3,求AD的长.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
[解] 因为AB⊥l,CD⊥l,二面角α-l-β的平面角为,
所以·=0,·=0,〈〉=.
因为=,
所以||2=()·()
=||2+||2+||2+2·+2·+2·
=||2+||2+||2+2·
=22+12+32+2×2×3×=20.
所以|AD|=2.
题号
1
3
5
2
4
6
8
7
2.(人教A版选择性必修第一册P38练习T4)如图,△ABC和△DBC所在平面垂直,且AB=BC=BD,∠CBA=∠DBC=120°.求:
(1)直线AD与直线BC所成角的大小;
(2)直线AD与平面BCD所成角的大小;
(3)平面ABD和平面BDC的夹角的余弦值.
题号
1
3
5
2
4
6
8
7
[解] 如图,建立空间直角坐标系.
设AB=a,则 A,
C(0,a,0),D,
∴=,
=(0,a,0),=.
(1)∵·=0,∴AD⊥BC,
∴直线AD与直线BC所成角的大小为90°.
(2)设AD与平面BCD所成的角为θ,
∵n=(0,0,1)是平面BCD的一个法向量,
∴sin θ=|cos 〈,n〉|===.
∴θ=45°,即直线AD与平面BCD所成角的大小为45°.
题号
1
3
5
2
4
6
8
7
(3)设m=(x,y,z)是平面ABD的法向量,
则∴
取x=1,则z=1,y=,∴m=(1,,1).
∴cos 〈m,n〉===.
设平面ABD和平面BDC的夹角为θ,则cos θ=|cos 〈m,n〉|=.
故平面ABD和平面BDC夹角的余弦值为.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
3.(人教A版选择性必修第一册P35练习T2)如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1)求点A1到直线B1E的距离;
(2)求直线FC1到直线AE的距离;
(3)求点A1到平面AB1E的距离;
(4)求直线FC1到平面AB1E的距离.
题号
1
3
5
2
4
6
8
7
[解] 建立如图所示的空间直角坐标系,则A1(1,0,1),B1(1,1,
1),E,F,C1(0,1,1),A(1,0,0).
(1)=,
u1===(0,1,0).
设a1==∴=1,a1·u1=-,
∴点A1到直线B1E的距离为==.
(2)∵==,
∴∴,
∴点F到直线AE的距离即为直线FC1到直线AE的距离.
u2===.
设a2==,∴=,a2·u2=.
∴直线FC1到直线AE的距离为=.
题号
1
3
5
2
4
6
8
7
(3)设平面AB1E的法向量为n=(x,y,z),
又=(0,1,1),=,
∴
取z=2,则y=-2,x=1,
∴n=(1,-2,2),∴n0==.
又=(0,0,1),∴点A1到平面AB1E的距离为|·n0|=.
题号
1
3
5
2
4
6
8
7
(4)∵FC1∥AE,FC1 平面AB1E,AE 平面AB1E,
∴FC1∥平面AB1E,
∴FC1到平面AB1E的距离即为F到平面AB1E的距离.
又平面AB1E的单位法向量n0==,
∴直线FC1到平面AB1E的距离为|·n0|=.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
4.(2024·上海卷)定义一个集合Ω,其元素是空间内的点,任取P1,P2,P3∈Ω,存在不全为0的实数λ1,λ2,λ3,使得λ1+λ2+λ3=0(其中O为坐标原点).已知(1,0,0)∈Ω,则(0,0,1) Ω的充分条件是( )
A.(0,0,0)∈Ω B.(-1,0,0)∈Ω
C.(0,1,0)∈Ω D.(0,0,-1)∈Ω
√
题号
1
3
5
2
4
6
8
7
C [由题意知这三个向量共面,即这三个向量不能构成空间的一个基底,
对A,由空间直角坐标系易知(0,0,0),(1,0,0),(0,0,1)三个向量共面,则当(0,0,0),(1,0,0)∈Ω无法推出(0,0,1) Ω,故A错误;
对B,由空间直角坐标系易知(-1,0,0),(1,0,0),(0,0,1)三个向量共面,则当(-1,0,0),(1,0,0)∈Ω无法推出(0,0,1) Ω,故B错误;
对C,由空间直角坐标系易知(1,0,0),(0,0,1),(0,1,0)三个向量不共面,可构成空间的一个基底,
则由(1,0,0),(0,1,0)∈Ω能推出(0,0,1) Ω,
对D,由空间直角坐标系易知(1,0,0),(0,0,1),(0,0,-1)三个向量共面,
则当(0,0,-1),(1,0,0)∈Ω无法推出(0,0,1) Ω,故D错误.故选C.]
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
5.(2024·全国甲卷)如图,在以A,B,C,D,E,F为顶点的五面体中,四边形ABCD与四边形ADEF均为等腰梯形,BC∥AD,EF∥AD,AD=4,AB=BC=EF=2,ED=,FB=2,M为AD的中点.
(1)证明:BM∥平面CDE;
(2)求二面角F-BM-E的正弦值.
题号
1
3
5
2
4
6
8
7
[解] (1)证明:因为BC∥AD,BC=2,AD=4,M为AD的中点,所以BC∥MD,BC=MD,
所以四边形BCDM为平行四边形,所以BM∥CD,又因为BM 平面CDE,
CD 平面CDE,所以BM∥平面CDE.
(2)如图所示,作BO⊥AD交AD于点O,连接OF,
因为四边形ABCD为等腰梯形,BC∥AD,
AD=4,AB=BC=2,所以CD=2,
结合(1)四边形BCDM为平行四边形,
可得BM=CD=2,又AM=2,
所以△ABM为等边三角形,O为AM的中点,所以OB=.
又因为四边形ADEF为等腰梯形,M为AD中点,所以EF=MD,EF∥MD,
四边形EFMD为平行四边形,FM=ED=AF,
题号
1
3
5
2
4
6
8
7
所以△AFM为等腰三角形,△ABM与△AFM底边上中点O重合,OF⊥AM,OF==3.
又因为BF=2,则OB2+OF2=BF2,所以OB⊥OF,所以OB,OD,OF互相垂直,
以为x轴正方向,为y轴正方向,为z轴正方向,建立空间直角坐标系,
则F (0,0,3),B(,0,0),M(0,1,0),E(0,2,3),=
(-,1,0),=(-,0,3),
题号
1
3
5
2
4
6
8
7
=(-,2,3),设平面BFM的法向量为m=(x1,y1,z1),
则即
令x1=,得y1=3,z1=1,
即m=(,3,1)是平面BFM的一个法向量,
设平面EMB的法向量为n=(x2,y2,z2),
则即
题号
1
3
5
2
4
6
8
7
令x2=,得y2=3,z2=-1,
即n=(,3,-1)是平面EMB的一个法向量,
则cos 〈m,n〉===,
则sin 〈m,n〉=,
故二面角F-BM-E的正弦值为.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
6.(2023·新高考Ⅰ卷)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.
(1)证明:B2C2∥A2D2;
(2)点P在棱BB1上,当二面角P-A2C2-D2为150°时,
求B2P.
题号
1
3
5
2
4
6
8
7
[解] (1)证明:以点C为坐标原点,CD,CB,CC1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,则B2(0,2,2),C2(0,0,3),A2(2,2,1),D2(2,0,2),
所以=(0,-2,1),
=(0,-2,1),
所以=,所以B2C2∥A2D2.
(2)设BP=n(0≤n≤4),则P(0,2,n),
所以=(2,0,1-n),=(0,-2,3-n),
设平面PA2C2的法向量为a=(x1,y1,z1),
所以则
令x1=n-1,得a=(n-1,3-n,2).
设平面A2C2D2的法向量为b=(x2,y2,z2),
又=(-2,-2,2),=(0,-2,1),
题号
1
3
5
2
4
6
8
7
所以则
令y2=1,得b=(1,1,2).
所以|cos 150°|=|cos 〈a,b〉|
==,
整理得n2-4n+3=0,解得n=1或n=3,所以BP=1或BP=3,
所以B2P=1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
7.(2024·天津卷)如图,已知直四棱柱ABCD-A1B1C1D1中,AD⊥AB,AB∥CD,AA1=2,AB=2AD=2,DC=1,N是B1C1的中点,M是DD1的中点.
(1)求证:D1N∥平面CB1M;
(2)求平面CB1M与平面BB1C1C夹角的余弦值;
(3)求点B到平面CB1M的距离.
题号
1
3
5
2
4
6
8
7
[解] (1)证明:取CB1的中点P,连接NP,MP,
由N是B1C1的中点,故NP∥CC1,且NP=CC1,
由M是DD1的中点,故D1M=DD1=CC1,且D1M∥CC1,
则有D1M∥NP,D1M=NP,
故四边形D1MPN是平行四边形,故D1N∥MP.
又MP 平面CB1M,D1N 平面CB1M,
故D1N∥平面CB1M.
(2)由题意知,AA1,AB,AD两两垂直,以A为原点建立如图所示空间直角坐标系,
则A(0,0,0),B(2,0,0),B1(2,0,2),
M(0,1,1),C(1,1,0),C1(1,1,2),
则有=(1,-1,2),=(-1,0,1),
=(0,0,2).
设平面CB1M与平面BB1C1C的法向量分别为m=(x1,y1,z1),n=(x2,y2,z2),
题号
1
3
5
2
4
6
8
7
则有
分别取x1=x2=1,则有y1=3,
z1=1,y2=1,z2=0,即m=(1,3,1),n=(1,1,0),
设平面CB1M与平面BB1C1C的夹角为θ,
则cos θ=|cos 〈m,n〉|===,
故平面CB1M与平面BB1C1C夹角的余弦值为.
题号
1
3
5
2
4
6
8
7
(3)由=(0,0,2),平面CB1M的一个法向量m=(1,3,1),
则有==,
即点B到平面CB1M的距离为.
题号
1
3
5
2
4
6
8
7
8.(2022·新高考Ⅰ卷)如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面积为2 .
(1)求A到平面A1BC的距离;
(2)设D为A1C的中点,AA1=AB,平面A1BC⊥
平面ABB1A1,求二面角A-BD-C的正弦值.
题号
1
3
5
2
4
6
8
7
题号
1
3
5
2
4
6
8
7
[解] (1)在直三棱柱ABC-A1B1C1中,设点A到平面A1BC的距离为h,
则=·h=h==·S△ABC·A1A==,
解得h=,
所以点A到平面A1BC的距离为.
(2)取A1B的中点E,连接AE,因为AA1=AB,所以AE⊥A1B,又平面A1BC⊥平面ABB1A1,平面A1BC∩平面ABB1A1=A1B,且AE 平面ABB1A1,所以AE⊥平面A1BC,在直三棱柱ABC - A1B1C1中,BB1⊥平面ABC,由BC 平面A1BC,BC 平面ABC,可得AE⊥BC,BB1⊥BC,又AE,BB1 平面ABB1A1且相交,所以BC⊥平面ABB1A1,所以BC,BA,BB1两两垂直,以B为原点,建立空间直角坐标系,如图,
题号
1
3
5
2
4
6
8
7
由(1)得AE=,所以AA1=AB=2,A1B=2 ,所以BC=2,
则A(0,2,0),A1(0,2,2),B(0,0,0),C(2,0,0),所以A1C的中点D(1,1,1),
则=(1,1,1),=(0,2,0),=(2,0,0).
设平面ABD的法向量m=(x,y,z),
则可取m=(1,0,-1),
题号
1
3
5
2
4
6
8
7
设平面BDC的法向量n=(a,b,c),
则可取n=(0,1,-1),
则cos 〈m,n〉===,
所以二面角A-BD-C的正弦值为=.
题号
1
3
5
2
4
6
8
7
谢 谢 !
同课章节目录
