《高考快车道》2026版高三一轮总复习数学(基础版)85 第八章 第4课时 直线与圆、圆与圆的位置关系 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)85 第八章 第4课时 直线与圆、圆与圆的位置关系 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:02 | ||
图片预览











文档简介
(共99张PPT)
第八章 解析几何
第4课时 直线与圆、圆与圆的位置关系
[考试要求] 1.能根据给定直线、圆的方程判断直线与圆、圆与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
[考试要求] 1.能根据给定直线、圆的方程判断直线与圆、圆与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
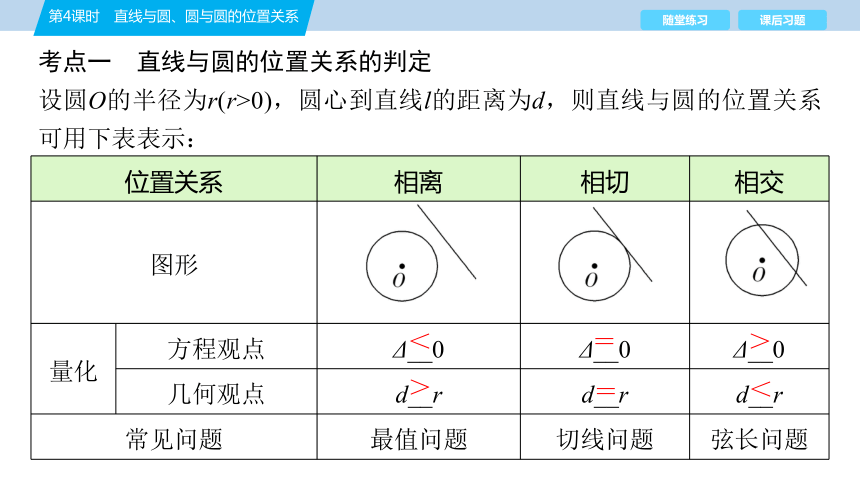
考点一 直线与圆的位置关系的判定
设圆O的半径为r(r>0),圆心到直线l的距离为d,则直线与圆的位置关系可用下表表示:
位置关系 相离 相切 相交
图形
量化 方程观点 Δ__0 Δ__0 Δ__0
几何观点 d__r d__r d__r
常见问题 最值问题 切线问题 弦长问题
<
=
>
>
=
<
[常用结论]
圆的切线方程常用结论
(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.如图1.
(2)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线的方程为x0x+y0y=r2.如图2.
考向1 直线与圆位置关系的判断
[典例1] (人教A版选择性必修第一册P91例1改编)直线l:mx-y+1-m=0与圆C:x2+(y-1)2=5的位置关系是( )
A.相交 B.相切
C.相离 D.不确定
√
A [法一(代数法):由消去y,
整理得(1+m2)x2-2m2x+m2-5=0,
因为Δ=16m2+20>0,所以直线l与圆相交.故选A.
法二(几何法):由题意知,圆心(0,1)到直线l的距离为d=<1<=r,所以直线l与圆相交.故选A.
法三(定点法):直线l:mx-y+1-m=0,整理得m(x-1)+1-y=0,恒过定点(1,1),而1+(1-1)2<5,即(1,1)在圆内,所以直线l与圆相交.故选A.]
链接·2025高考试题
(2025·全国一卷)已知圆x2+(y+2)2=r2(r>0)上到直线y=x+2的距离为1的点有且仅有两个,则r的取值范围是( )
A.(0,1) B.(1,3)
C.(3,+∞) D.(0,+∞)
√
B [由题意得圆心(0,-2)到直线y=x+2的距离d=2.当r=d-1=1时,圆x2+(y+2)2=r2(r>0)上到直线y=x+2的距离为1的点有且仅有一个,当r=d+1=3时,圆x2+(y+2)2=r2(r>0)上到直线y=x+2的距离为1的点有且仅有三个,故当10)上到直线y=x+2的距离为1的点有且仅有两个.故选B.]
反思领悟 判断直线与圆的位置关系的常见方法
(1)代数法:联立方程之后利用Δ判断.
(2)几何法:利用圆心到直线的距离与半径的关系.
(3)点与圆的位置关系法(定点法):若直线恒过定点且定点在圆内,可判断直线与圆相交.
巩固迁移1 已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
√
B [因为M(a,b)在圆O:x2+y2=1外,
所以a2+b2>1,
而圆心O到直线ax+by=1的距离d==<1,
所以直线与圆相交.故选B.]
【教用·备选题】
(多选)(经典题)已知直线l:ax+by-r2=0(r>0)与圆C:x2+y2=r2,点A(a,b),则下列说法正确的是( )
A.若点A在圆C上,则直线l与圆C相切
B.若点A在圆C内,则直线l与圆C相离
C.若点A在圆C外,则直线l与圆C相离
D.若点A在直线l上,则直线l与圆C相切
√
√
√
ABD [对于A,∵点A在圆C上,∴a2+b2=r2,圆心C(0,0)到直线l的距离d==r,∴直线l与圆C相切,A正确.
对于B,∵点A在圆C内,∴a2+b2<r2,圆心C(0,0)到直线l的距离d=>r,∴直线l与圆C相离,B正确.
对于C,∵点A在圆C外,∴a2+b2>r2,圆心C(0,0)到直线l的距离d=<r,∴直线l与圆C相交,C错误.
对于D,∵点A在直线l上,∴a2+b2=r2,圆心C(0,0)到直线l的距离d==r,∴直线l与圆C相切,D正确.
故选ABD.]
考向2 切线问题
[典例2] 已知点P(+1,2-),点M(3,1),圆C:(x-1)2+(y-2)2=4.
(1)求过点P的圆C的切线方程;
(2)求过点M的圆C的切线方程,并求出切线长.
[解] 由题意得圆心C(1,2),半径r=2.
(1)因为(+1-1)2+(2--2)2=4,所以点P在圆C上.
又kPC==-1,所以所求切线的斜率k=-=1.
所以过点P的圆C的切线方程是y-(2-)=x-(+1),即x-y+1-2=0.
(2)因为(3-1)2+(1-2)2=5>4,
所以点M在圆C外部.
当过点M的直线斜率不存在时,
直线方程为x=3,即x-3=0.
又点C(1,2)到直线x-3=0的距离d=3-1=2=r,
即此时满足题意,所以直线x=3是圆C的切线.
当切线的斜率存在时,
设切线方程为y-1=k(x-3),
即kx-y+1-3k=0,
则圆心C到切线的距离d==r=2,解得k=.
所以切线方程为y-1=(x-3),
即3x-4y-5=0.
综上可得,过点M的圆C的切线方程为x-3=0或3x-4y-5=0.
因为|MC|==,
所以过点M的圆C的切线长为==1.
反思领悟 (1)本例(1)中,点P在圆上,求圆的切线方程的关键是利用点P与圆心C的连线与切线垂直求切线斜率.
(2)本例(2)中,点M在圆外,求圆的切线方程一般用几何法.当切线斜率存在时,设切线方程为y-1=k(x-3),利用点到直线的距离公式表示出圆心(1,2)到切线的距离d,然后令d=r=2,进而求出切线斜率k.要注意验证斜率不存在的情况.
(3)求切线长,常利用点M、圆心C、切点构成的直角三角形求解.
巩固迁移2 (2025·北京市东城区模拟)已知点M(1,)在圆C:x2+y2=m上,过M作圆C的切线l,则l的倾斜角为( )
A.30° B.60°
C.120° D.150°
√
D [由题意得m=1+3=4,
当l的斜率不存在时,此时过M的直线方程为x=1,与圆C:x2+y2=4相交,不符合题意;
当l的斜率存在时,设切线l的方程为y-=k(x-1),
则=2,解得k=-,因为l的倾斜角的范围为0°≤θ<180°,
故l的倾斜角为150°.]
考向3 弦长问题
[典例3] (2024·保定月考)已知直线l:(m-1)x+2y+3-m=0与圆C:x2+y2-6x+6y=0交于A,B两点,则线段AB的长度的取值范围是( )
A.[,3] B.[2,6]
C.[2,4] D.[,6]
√
B [圆C:x2+y2-6x+6y=0可得圆心C(3,-3),半径r=3,
因为直线l:(m-1)x+2y+3-m=0,恒过直线x-1=0和-x+2y+3=0的交点,
即解得x=1,y=-1,
即直线l恒过定点P(1,-1),
因为12+(-1)2-6-6<0,所以定点P在圆内,
设圆心C到直线l的距离为d,则弦长|AB|=2,
当d=0时,弦长最大,这时过P的弦长最长,为圆的直径2r=6,
当d最大时,dmax=|PC|==2,
所以弦长的最小值为|AB|min=2=2=2,
所以线段AB的长度的取值范围为[2,6].故选B.]
反思领悟 求圆的弦长一般用几何法;若弦心距为d,圆的半径为r,则弦长|AB|=2.由此可知,本例中,当d=0,即直线过圆心时,|AB|最长;当PC⊥l时,d最大,|AB|最短.
巩固迁移3 (人教A版选择性必修第一册P98习题2.5T3改编)直线m:x+y-1=0被圆M:x2+y2-2x-4y=0截得的弦长为( )
A.4 B.2
C. D.
√
B [∵x2+y2-2x-4y=0,
∴(x-1)2+(y-2)2=5,
∴圆M的圆心坐标为(1,2),半径为.
又点(1,2)到直线x+y-1=0的距离d==,
∴直线m被圆M截得的弦长等于2=2.]
考向4 直线与圆位置关系中的最值问题
[典例4] (2024·曲靖市会泽县期末)过直线x-2y+5=0上一点P向圆C:(x-1)2+(y+2)2=4作切线,切点为M,则|PM|的最小值为________.
4
4 [根据题意,圆C:(x-1)2+(y+2)2=4,其圆心C的坐标为(1,
-2),半径r=2,
圆心C到直线x-2y+5=0的距离d=
=2>2,
所以直线与圆相离,
因为△PCM为直角三角形,且PM⊥CM,
所以|PM|==4,
当且仅当PC与直线x-2y+5=0垂直时,等号成立,
所以|PM|的最小值为4.]
反思领悟 解答本题的关键是能够把所求线段长|PM|表示为圆心与直线上的点之间的距离的函数|PM|=的形式,然后利用求函数值域的方法求得最小值.
巩固迁移4 过直线x-y-m=0上一点P作圆M:(x-2)2+(y-3)2=1的两条切线,切点分别为A,B,若使得四边形PAMB的面积为的点P有两个,则实数m的取值范围为( )
A.(-5,3)
B.(-3,5)
C.(-∞,-5)∪(3,+∞)
D.(-∞,-3)∪(5,+∞)
√
A [由圆M:(x-2)2+(y-3)2=1可知,圆心M(2,3),半径为1,
所以|MA|=|MB|=1,
所以四边形PAMB的面积为S=|PA||MA|+|PB|·|MB|=|PA|=,
所以|PM|===2,
要使四边形PAMB的面积为的点P有两个,
则<2,解得-5考点二 圆与圆的位置关系
若两圆的半径分别为r1,r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下:
外离 外切 相交 内切 内含
图形
量的关系 d>______ d=______ |r1-r2|<d<r1+r2 d=______ d<______
r1+r2
r1+r2
|r1-r2|
|r1-r2|
[常用结论]
1.两圆相交时公共弦所在直线的方程
设圆C1:x2+y2+D1x+E1y+F1=0,①
圆C2:x2+y2+D2x+E2y+F2=0,②
若两圆相交,则有一条公共弦,其公共弦所在直线方程由①-②所得,即(D1-D2)x+(E1-E2)y+(F1-F2)=0.
2.两个圆系方程
(1)过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ∈R).
(2)过圆C1:x2+y2+D1x+E1y+F1=0和圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1)(该圆系不含圆C2,解题时,注意检验圆C2是否满足题意,以防漏解).
考向1 两圆位置关系的判断
[典例5] (2024·泊头市月考)已知圆C1:x2+(y-3)2=4与圆C2:x2+y2-6x+2y+1=0,则圆C1与圆C2的位置关系为( )
A.相交 B.外切
C.外离 D.内含
√
B [圆C1:x2+(y-3)2=4,圆心C1(0,3),半径r1=2,
圆C2:x2+y2-6x+2y+1=0可化为(x-3)2+(y+1)2=9,圆心C2(3,-1),半径r2=3,
则|C1C2|==5=2+3=r1+r2,
故圆C1与圆C2的位置关系为外切.故选B.]
反思领悟 判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.
巩固迁移5 (2025·北京市朝阳区模拟)已知圆E:(x-2)2+(y-4)2=25,圆F:(x-2)2+(y-2)2=1,则这两圆的位置关系为( )
A.内含 B.相切
C.相交 D.外离
√
A [圆E:(x-2)2+(y-4)2=25的圆心为E(2,4),半径r1=5,
圆F:(x-2)2+(y-2)2=1的圆心为F (2,2),半径r2=1,
因为圆心距|EF|==2,
且|EF|<|r1-r2|=4,所以两圆的位置关系为内含.
故选A.]
考向2 圆系方程
[典例6] (2024·沈阳市皇姑区期末)圆心在直线x-y-4=0上,且经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点的圆的方程为
( )
A.x2+y2-x+7y-32=0
B.x2+y2-x+7y-16=0
C.x2+y2-4x+4y+9=0
D.x2+y2-4x+4y-8=0
√
A [根据题意,要求圆经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点,
设其方程为(x2+y2+6x-4)+λ(x2+y2+6y-28)=0,
变形可得(1+λ)x2+(1+λ)y2+6x+6λy-4-28λ=0,
其圆心为,又由圆心在直线x-y-4=0上,
则有--4=0,解得λ=-7,
所以圆的方程为-6x2-6y2+6x-42y+192=0,
即x2+y2-x+7y-32=0,故选A.]
反思领悟 过两圆x2+y2+6x-4=0和x2+y2+6y-28=0交点的圆系方程为+y2+6y-28)=0.当λ=
-1时,这一方程为一次方程,两圆相交时,表示公共弦所在直线方程,两圆相切时,表示公切线所在直线方程.
巩固迁移6 (2025·太原市尖草坪区模拟)过点M(2,-1),且经过圆x2+y2-4x-4y+4=0与圆x2+y2-4=0的交点的圆的方程为( )
A.x2+y2+x+y-6=0
B.x2+y2+x-y-8=0
C.x2+y2-x+y-2=0
D.x2+y2-x-y-4=0
√
A [设经过圆x2+y2-4x-4y+4=0与圆x2+y2-4=0的交点的圆的方程为
(x2+y2-4x-4y+4)+λ(x2+y2-4)=0,
由题意将M的坐标代入可得(4+1-8+4+4)+λ(4+1-4)=0,
解得λ=-5,所以所求圆的方程为x2+y2+x+y-6=0,故选A.]
考向3 公切线、公共弦问题
[典例7] 已知两圆C1:x2+y2-2x+10y-24=0和C2:x2+y2+2x+2y-8=0.
(1)判断两圆公切线的条数;
(2)求公共弦所在的直线方程以及公共弦的长度.
[解] (1)两圆的标准方程分别为
C1:(x-1)2+(y+5)2=50,
C2:(x+1)2+(y+1)2=10,
则圆C1的圆心坐标为(1,-5),半径r1=5;
圆C2的圆心坐标为(-1,-1),半径r2=.
又|C1C2|=2,r1+r2=5,r1-r2=5,
所以r1-r2<|C1C2|所以两圆有两条公切线.
(2)将两圆方程相减,得公共弦所在直线方程为x-2y+4=0.
圆心C1到直线x-2y+4=0的距离d==3,
设公共弦长为2l,由勾股定理得=d2+l2,
得50=45+l2,解得l=,所以公共弦的长度为2l=2.
反思领悟 本例(1)中两圆相交,有两条公切线;本例(2),两圆方程作差消去x2,y2项得到x,y的二元一次方程即为公共弦所在直线方程;求公共弦长,常选其中一圆,由圆心到公共弦的距离d,半弦长l,半径r构成直角三角形,利用勾股定理求解.
巩固迁移7 (2025·金华市金东区模拟)圆C1:x2+y2=1与圆C2:x2+y2+2x-2y+1=0的公共弦长为( )
A. B.
C. D.1
√
B [两圆的圆心坐标分别为(0,0),(-1,1),半径均为1,故两圆的圆心距为,0<<2,故两圆相交,
∴圆x2+y2=1与圆x2+y2+2x-2y+1=0的公共弦所在直线的方程为
(x2+y2+2x-2y+1)-(x2+y2-1)=2x-2y+2=0,即x-y+1=0,
∵圆C1:x2+y2=1的圆心C1(0,0)到公共弦x-y+1=0的距离为d=
=,圆C1的半径r=1,∴公共弦长为2=.
故选B.]
随堂练习
√
1.(人教A版选择性必修第一册P91例1改编)圆(x-1)2+(y+2)2=6与直线2x+y-5=0的位置关系是( )
A.相切
B.相离
C.相交且直线过圆心
D.相交但直线不过圆心
D [由题意知圆心(1,-2)到直线2x+y-5=0的距离d==<,且2×1+(-2)-5≠0,所以直线与圆相交但不过圆心.故选D.]
2.(2024·上海市长宁区期末)圆A:x2+y2-8x+6y+16=0与圆B:x2+y2=64的位置关系是( )
A.相交 B.内切
C.相离 D.外切
√
B [把圆A:x2+y2-8x+6y+16=0化为标准方程得(x-4)2+(y+3)2=9,
∴圆心A的坐标为(4,-3),半径r=3,
由圆B:x2+y2=64,得到圆心B的坐标为(0,0),半径R=8,
两圆心间的距离d=|AB|=5,
∵8-3=5,即d=R-r,∴两圆的位置关系是内切.故选B.]
3.(2025·哈尔滨市香坊区模拟)已知圆C1:x2+y2=4,圆C2:x2+y2-4x-4y+4=0,两圆的公共弦所在直线的方程是( )
A.x+y+2=0 B.x+y-2=0
C.x+y+1=0 D.x+y-1=0
√
B [由圆C1:x2+y2=4,圆C2:x2+y2-4x-4y+4=0,
两式作差得4x+4y-4=4,即x+y-2=0,
所以两圆的公共弦所在直线的方程是x+y-2=0.故选B.]
4.(人教A版选择性必修第一册P92例2改编)圆x2+y2-4x=0在点P(1,)处的切线方程为_____________.
x-y+2=0 [圆的方程为(x-2)2+y2=4,圆心坐标为(2,0),半径为2,点P在圆上,所以点P与圆心连线的斜率为-,所以过点P
的切线的斜率为,所以切线方程为y-=(x-1),即x-y+
2=0.]
x-y+2=0
链接·2025高考试题
(2025·天津卷) l1:x-y+6=0与x轴交于点A,与y轴交于点B,与圆(x+1)2+(y-3)2=r2(r>0)交于C,D两点,|AB|=3|CD|,则r=________.
2
2 [对于直线l1:x-y+6=0,令x=0,得y=6,令y=0,得x=
-6,所以A(-6,0),B(0,6),所以|AB|=6.因为|AB|=3|CD|,所以|CD|=2.圆(x+1)2+(y-3)2=r2的圆心为(-1,3),圆心到直线l1的距离d==,所以r===2.]
【教用·备选题】
1.(2024·重庆市渝中区期末)已知圆C1:(x-a)2+(y-1)2=1与圆C2:(x-1)2+(y-3)2=4有且仅有2条公切线,则实数a的取值范围是
( )
A.(1-,1+) B.(1+,1+)
C.(-2,0) D.(1-,1+)
√
A [由圆C1:(x-a)2+(y-1)2=1与圆C2:(x-1)2+(y-3)2=4有且仅有2条公切线可知两圆的位置关系为相交,所以|r1-r2|<|C1C2|<r1
+r2,即1<<3,
平方得1<a2-2a+5<9,
解得1-故选A.]
2.(2024·濮阳市南乐县月考)已知直线l:y=x+a与圆x2+y2=2和圆(x-4)2+y2=m2(m>0)都相切,则实数m的值为( )
A. B.2
C.3 D.或3
√
D [因为直线l:y=x+a与圆x2+y2=2相切,
所以=,解得a=±2,
因为直线l:y=x±2和圆(x-4)2+y2=m2(m>0)相切,
所以=m或=m,
解得m=3或m=,
故实数m的值为3或.
故选D.]
3.(2025·宜宾模拟)已知点P是直线x+y+3=0上一动点,过点P作圆C:(x+1)2+y2=1的两条切线,切点为A,B,则弦AB长度的最小值为( )
A.1 B.
C.2 D.2
√
B [易知当弦AB最小时,∠ACB最小,
则|PC|最小,
而|PC|的最小值为圆心C到直线x+y+3=0的距离,
即=,此时cos ∠ACP==,
则sin ∠ACP===|AB|,
解得|AB|=.故选B.]
4.(2024·绵阳市开学考试)已知A(0,-2),B(2,0),点P为圆C:x2+y2-2x-8y+13=0上任意一点,则△PAB面积的最大值为( )
A.5 B.5-2
C. D.5+2
√
D [圆x2+y2-2x-8y+13=0的圆心C(1,4),半径r=2,
直线AB的方程为y=x-2,
于是点C到直线AB:x-y-2=0的距离
d==,而点P在圆C上,
因此点P到直线AB距离的最大值为+2,
又|AB|==2,所以△PAB面积的最大值为S=×2=5+2.故选D.]
5.(2024·郴州期末)若直线l:kx-y+2-2k=0与曲线C:y=有两个不同的交点,则实数k的取值范围是________.
[由题意可得直线l:kx-y+2-2k=0即y=k(x-2)+2,
所以直线l恒过定点A(2,2),
曲线C:y=为以(0,0)为圆心,
2为半径的上半圆(包含x轴部分),
它们的图象如图所示.
当直线l过点(-2,0)时,它们有两个交点,此时k==,
当直线l与上半部分圆相切时,有一个交点,此时k=0,
由图象可知,若直线l与曲线C有两个不同的交点,则0即实数k的取值范围是.]
课后习题(五十三) 直线与圆、圆与圆的位置关系
1.(人教A版选择性必修第一册P92例2改编)由直线x-y+4=0上一点P向圆C:(x-1)2+(y-1)2=1引切线,则切线长的最小值为( )
A. B.3
C.2 D.2-1
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [圆(x-1)2+(y-1)2=1的圆心C(1,1),半径为1,由直线x-y+4=0上一点P向圆(x-1)2+(y-1)2=1引切线,设切点为M,连接PC,MC(图略),则|PM|==,要使切线长最小,则|PC|最小,而|PC|的最小值等于圆心C到直线x-y+4=0的距离,故|PC|min==2,
故切线长的最小值为=.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教B版选择性必修第一册P120探索与研究改编)圆x2-4x+y2=0与圆x2+y2+4x+3=0的公切线共有( )
A.1条 B.2条
C.3条 D.4条
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由x2-4x+y2=0,得(x-2)2+y2=22,则圆心坐标为(2,0),半径为2;由x2+y2+4x+3=0,得(x+2)2+y2=12,则圆心坐标为
(-2,0),半径为1.
故两圆的圆心距为4,半径之和为3,
因为4>3,所以两圆的位置关系是外离,故两圆的公切线共有4条.
故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(多选)(人教A版选择性必修第一册P98练习T2改编)已知圆O1:x2+y2-2x=0和圆O2:x2+y2+2x-8y=0的交点为A,B,则下列结论正确的是( )
A.直线AB的方程为x-2y=0
B.|AB|=
C.线段AB的垂直平分线方程为2x+y-2=0
D.若点P为圆O1上的一个动点,则点P到直线AB的距离的最大值为+1
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ACD [根据题意,由x2+y2-2x=0,得(x-1)2+y2=1,则圆心O1(1,0),半径r=1,由x2+y2+2x-8y=0,得(x+1)2+(y-4)2=17,则圆心O2(-1,4),半径R=.
对于A,联立得x-2y=0,
即直线AB的方程为x-2y=0,A正确;对于B,圆心O1到直线AB的
距离d==,则|AB|=2×=,B错误;
对于C,线段AB的垂直平分线即直线O1O2,由O1(1,0),O2(-1,4),易得直线O1O2的方程为2x+y-2=0,C正确;对于D,由圆心
O1到直线AB的距离d=,知点P到直线AB的距离的最大值为+
1,D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第一册P92例2改编)过点A(3,5)作圆O:x2+y2-2x-4y+1=0的切线,则切线的方程为_____________________
____.
5x-12y+45=0或x-3
=0
题号
1
3
5
2
4
6
8
7
9
10
11
12
5x-12y+45=0或x-3=0 [圆x2+y2-2x-4y+1=0化为标准方程得(x-1)2+(y-2)2=4,则圆心O(1,2),半径为2,
因为|OA|==>2,所以点A(3,5)在圆外.显然,当切线斜率不存在时,直线与圆相切,即切线方程为x-3=0;当切线斜率存在时,设所求切线方程为y-5=k(x-3),即kx-y+5-3k=0.又圆心为(1,2),半径r=2,而圆心到切线的距离d==2,即|3-2k|=2,解得k=,此时直线方程为5x-12y+45=0.
故所求切线方程为5x-12y+45=0或x-3=0.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2025·唐山模拟)已知直线l:x-y+2=0,圆C:x2+y2=r2(r>0),若圆C上恰有三个点到直线l的距离等于,则r=( )
A.2 B.4
C.2 D.8
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [圆心C(0,0),则点C到直线l的距离d==,又因为圆C上恰有三个点到直线l的距离为,所以圆心到直线l的距离d=,
即r=2d=2.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·重庆市沙坪坝区期末)过点P(-1,1)的直线l与圆C:x2+y2+4x-2=0交于A,B两点,则|AB|的最小值为( )
A.2 B.
C.4 D.2
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [圆C的标准方程为(x+2)2+y2=6,圆心C(-2,0),半径r=,
因为(-1+2)2+12<6,所以点P(-1,1)在圆C内,
设圆心C到直线l的距离为d,则|AB|=2,
当d=|CP|,即CP⊥l时,|AB|取得最小值,
因为|CP|==,
所以|AB|的最小值为2=4.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(多选)(2025·菏泽市牡丹区模拟)已知直线l:x+my-m+2=0,圆C:(x-1)2+(y-2)2=5,则下列说法正确的是( )
A.直线l恒过定点(-2,1)
B.直线l与圆C相交
C.当直线l平分圆C时,m=-3
D.当点C到直线l的距离最大时,m=
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ACD [对于A,l:x+my-m+2=0,即x+2+m(y-1)=0,
令y-1=0,有y=1,x=-2,所以直线l恒过定点P(-2,1),故A正确;
对于B,圆C:(x-1)2+(y-2)2=5的圆心C(1,2),半径r=,
点C(1,2)到直线l:x+my-m+2=0的距离为d=,
从而d2-r2=-5==,
取m=2,则此时有d=r,即圆C与直线l相切,故B错误;
对于C,当直线l平分圆C时,点C(1,2)在直线l:x+my-m+2=0上,
即1+2m-m+2=0成立,解得m=-3,故C正确;
对于D,点C到直线l的距离满足d≤|PC|,当且仅当PC⊥l时,等号成立,
而PC的斜率为k==,
所以当等号成立时有·=-1,解得m=,故D正确.
故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·连云港期末)已知圆C:x2+y2-4y+2=0,则下列说法正确的有( )
A.圆C关于直线x-y=0对称的圆的方程为(x-2)2+y2=2
B.直线x-y+1=0被圆C截得的弦长为
C.若圆C上有四个点到直线x-y+m=0的距离等于,则m的取值范围
是(1,3)
D.若点P(x,y)是圆C上的动点,则x2+y2的取值范围是[2-,2+]
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AC [A项,圆C:x2+y2-4y+2=0,即为x2+(y-2)2=2,圆心为(0,2),半径为,
因为(0,2)关于直线x-y=0对称的坐标为(2,0),则圆C关于直线x-y=0的对称圆的方程为(x-2)2+y2=2,故A正确;
B项,圆心C(0,2)到直线x-y+1=0的距离为,
则所求弦长为2=,故B错误;
题号
1
3
5
2
4
6
8
7
9
10
11
12
C项,由题意有圆心C到直线x-y+m=0的距离小于r-,
即<=,
∴|m-2|<1,∴1<m<3,
则m的取值范围是(1,3),故C正确;
D项,根据圆的标准方程,可设x=cos α,y=sin α+2,
x2+y2=2sin2α+2sin2α+4+4sinα=6+4sin α,
则x2+y2的取值范围是[6-4,6+4],故D错误.
故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·淮北一模)已知圆O:x2+y2=9与圆C:x2+y2-4x-6y+9=0交于A,B两点,则直线AB的方程为_____________;△ABC的面积为________.
2x+3y-9=0
题号
1
3
5
2
4
6
8
7
9
10
11
12
2x+3y-9=0 [两圆的方程相减得4x+6y=18,化简得2x+3y
-9=0,故直线AB的方程为2x+3y-9=0.圆C:x2+y2-4x-6y+9=0变形得到(x-2)2+(y-3)2=4,圆心C(2,3),半径为2,
故圆心C(2,3)到直线AB的距离为d==,
则|AB|=2×=,
故△ABC的面积为|AB|·d==.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·南京市雨花台区三模)已知圆O:x2+y2=2,过点M(1,3)的直线l交圆O于A,B两点,且|AB|=2,则直线l的方程为___________________.
x=1或4x-3y+5=0 [当直线l的斜率不存在时,l的方程为x=1,
由可得或
所以|1-(-1)|=2=|AB|,符合题意;
x=1或4x-3y+5=0
题号
1
3
5
2
4
6
8
7
9
10
11
12
当直线l的斜率存在时,设l的方程为y-3=k(x-1),
因为|AB|=2,所以圆心(0,0)到直线l的距离d=,
由+d2=2,得k=,所以直线l的方程为y-3=(x-1),
则直线l的方程为x=1或4x-3y+5=0.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·江门市新会区月考)已知圆C的方程为x2+y2-2x-4y+2m=0.
(1)求实数m的取值范围;
(2)若直线x-2y-1=0与圆C相切,求实数m的值;
(3)若圆C与圆O:x2+y2=1相切,求实数m的值.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)x2+y2-2x-4y+2m=0,
可化为(x-1)2+(y-2)2=5-2m,
所以5-2m>0 m<,故m的取值范围为.
(2)由(1)知,圆心C(1,2),半径r=,
因为圆(x-1)2+(y-2)2=5-2m和直线x-2y-1=0相切,
所以=,解得m=.
(3)因为圆O:x2+y2=1与圆C相切,
所以|OC|=1+=或|OC|=|-1|=,
解得m=<或m=-<,
故实数m的值是或-.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·吉林期末)已知动点P与两个定点A(1,0),B(4,0)的距离的比是2.
(1)求动点P的轨迹C的方程;
(2)直线l过点(2,1),且被曲线C截得的弦长为2,求直线l的方程.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)设点P(x,y),
∵动点P与两个定点A(1,0),B(4,0)的距离的比是2,
∴=2,即|PA|=2|PB|,
则=2,化简得x2+y2-10x+21=0,
所以动点P的轨迹C的方程为(x-5)2+y2=4.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)由(1)可知点P的轨迹C是以(5,0)为圆心,2为半径的圆,
∵直线l被曲线C截得的弦长为2,
∴圆心(5,0)到直线l的距离d==1.
①当直线l的斜率不存在时,直线l的方程为x=2,此时圆心到直线l的距离是3,不符合题意;
②当直线l的斜率存在时,设直线l的方程为y-1=k(x-2),即kx-y-2k+1=0,
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以圆心(5,0)到直线l的距离d==1,
化简得9k2+6k+1=k2+1,解得k=0或k=-,
此时直线l的方程为y=1或3x+4y-10=0.
综上,直线l的方程是y=1或3x+4y-10=0.
谢 谢 !
第八章 解析几何
第4课时 直线与圆、圆与圆的位置关系
[考试要求] 1.能根据给定直线、圆的方程判断直线与圆、圆与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
[考试要求] 1.能根据给定直线、圆的方程判断直线与圆、圆与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
考点一 直线与圆的位置关系的判定
设圆O的半径为r(r>0),圆心到直线l的距离为d,则直线与圆的位置关系可用下表表示:
位置关系 相离 相切 相交
图形
量化 方程观点 Δ__0 Δ__0 Δ__0
几何观点 d__r d__r d__r
常见问题 最值问题 切线问题 弦长问题
<
=
>
>
=
<
[常用结论]
圆的切线方程常用结论
(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.如图1.
(2)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线的方程为x0x+y0y=r2.如图2.
考向1 直线与圆位置关系的判断
[典例1] (人教A版选择性必修第一册P91例1改编)直线l:mx-y+1-m=0与圆C:x2+(y-1)2=5的位置关系是( )
A.相交 B.相切
C.相离 D.不确定
√
A [法一(代数法):由消去y,
整理得(1+m2)x2-2m2x+m2-5=0,
因为Δ=16m2+20>0,所以直线l与圆相交.故选A.
法二(几何法):由题意知,圆心(0,1)到直线l的距离为d=<1<=r,所以直线l与圆相交.故选A.
法三(定点法):直线l:mx-y+1-m=0,整理得m(x-1)+1-y=0,恒过定点(1,1),而1+(1-1)2<5,即(1,1)在圆内,所以直线l与圆相交.故选A.]
链接·2025高考试题
(2025·全国一卷)已知圆x2+(y+2)2=r2(r>0)上到直线y=x+2的距离为1的点有且仅有两个,则r的取值范围是( )
A.(0,1) B.(1,3)
C.(3,+∞) D.(0,+∞)
√
B [由题意得圆心(0,-2)到直线y=x+2的距离d=2.当r=d-1=1时,圆x2+(y+2)2=r2(r>0)上到直线y=x+2的距离为1的点有且仅有一个,当r=d+1=3时,圆x2+(y+2)2=r2(r>0)上到直线y=x+2的距离为1的点有且仅有三个,故当1
反思领悟 判断直线与圆的位置关系的常见方法
(1)代数法:联立方程之后利用Δ判断.
(2)几何法:利用圆心到直线的距离与半径的关系.
(3)点与圆的位置关系法(定点法):若直线恒过定点且定点在圆内,可判断直线与圆相交.
巩固迁移1 已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )
A.相切 B.相交
C.相离 D.不确定
√
B [因为M(a,b)在圆O:x2+y2=1外,
所以a2+b2>1,
而圆心O到直线ax+by=1的距离d==<1,
所以直线与圆相交.故选B.]
【教用·备选题】
(多选)(经典题)已知直线l:ax+by-r2=0(r>0)与圆C:x2+y2=r2,点A(a,b),则下列说法正确的是( )
A.若点A在圆C上,则直线l与圆C相切
B.若点A在圆C内,则直线l与圆C相离
C.若点A在圆C外,则直线l与圆C相离
D.若点A在直线l上,则直线l与圆C相切
√
√
√
ABD [对于A,∵点A在圆C上,∴a2+b2=r2,圆心C(0,0)到直线l的距离d==r,∴直线l与圆C相切,A正确.
对于B,∵点A在圆C内,∴a2+b2<r2,圆心C(0,0)到直线l的距离d=>r,∴直线l与圆C相离,B正确.
对于C,∵点A在圆C外,∴a2+b2>r2,圆心C(0,0)到直线l的距离d=<r,∴直线l与圆C相交,C错误.
对于D,∵点A在直线l上,∴a2+b2=r2,圆心C(0,0)到直线l的距离d==r,∴直线l与圆C相切,D正确.
故选ABD.]
考向2 切线问题
[典例2] 已知点P(+1,2-),点M(3,1),圆C:(x-1)2+(y-2)2=4.
(1)求过点P的圆C的切线方程;
(2)求过点M的圆C的切线方程,并求出切线长.
[解] 由题意得圆心C(1,2),半径r=2.
(1)因为(+1-1)2+(2--2)2=4,所以点P在圆C上.
又kPC==-1,所以所求切线的斜率k=-=1.
所以过点P的圆C的切线方程是y-(2-)=x-(+1),即x-y+1-2=0.
(2)因为(3-1)2+(1-2)2=5>4,
所以点M在圆C外部.
当过点M的直线斜率不存在时,
直线方程为x=3,即x-3=0.
又点C(1,2)到直线x-3=0的距离d=3-1=2=r,
即此时满足题意,所以直线x=3是圆C的切线.
当切线的斜率存在时,
设切线方程为y-1=k(x-3),
即kx-y+1-3k=0,
则圆心C到切线的距离d==r=2,解得k=.
所以切线方程为y-1=(x-3),
即3x-4y-5=0.
综上可得,过点M的圆C的切线方程为x-3=0或3x-4y-5=0.
因为|MC|==,
所以过点M的圆C的切线长为==1.
反思领悟 (1)本例(1)中,点P在圆上,求圆的切线方程的关键是利用点P与圆心C的连线与切线垂直求切线斜率.
(2)本例(2)中,点M在圆外,求圆的切线方程一般用几何法.当切线斜率存在时,设切线方程为y-1=k(x-3),利用点到直线的距离公式表示出圆心(1,2)到切线的距离d,然后令d=r=2,进而求出切线斜率k.要注意验证斜率不存在的情况.
(3)求切线长,常利用点M、圆心C、切点构成的直角三角形求解.
巩固迁移2 (2025·北京市东城区模拟)已知点M(1,)在圆C:x2+y2=m上,过M作圆C的切线l,则l的倾斜角为( )
A.30° B.60°
C.120° D.150°
√
D [由题意得m=1+3=4,
当l的斜率不存在时,此时过M的直线方程为x=1,与圆C:x2+y2=4相交,不符合题意;
当l的斜率存在时,设切线l的方程为y-=k(x-1),
则=2,解得k=-,因为l的倾斜角的范围为0°≤θ<180°,
故l的倾斜角为150°.]
考向3 弦长问题
[典例3] (2024·保定月考)已知直线l:(m-1)x+2y+3-m=0与圆C:x2+y2-6x+6y=0交于A,B两点,则线段AB的长度的取值范围是( )
A.[,3] B.[2,6]
C.[2,4] D.[,6]
√
B [圆C:x2+y2-6x+6y=0可得圆心C(3,-3),半径r=3,
因为直线l:(m-1)x+2y+3-m=0,恒过直线x-1=0和-x+2y+3=0的交点,
即解得x=1,y=-1,
即直线l恒过定点P(1,-1),
因为12+(-1)2-6-6<0,所以定点P在圆内,
设圆心C到直线l的距离为d,则弦长|AB|=2,
当d=0时,弦长最大,这时过P的弦长最长,为圆的直径2r=6,
当d最大时,dmax=|PC|==2,
所以弦长的最小值为|AB|min=2=2=2,
所以线段AB的长度的取值范围为[2,6].故选B.]
反思领悟 求圆的弦长一般用几何法;若弦心距为d,圆的半径为r,则弦长|AB|=2.由此可知,本例中,当d=0,即直线过圆心时,|AB|最长;当PC⊥l时,d最大,|AB|最短.
巩固迁移3 (人教A版选择性必修第一册P98习题2.5T3改编)直线m:x+y-1=0被圆M:x2+y2-2x-4y=0截得的弦长为( )
A.4 B.2
C. D.
√
B [∵x2+y2-2x-4y=0,
∴(x-1)2+(y-2)2=5,
∴圆M的圆心坐标为(1,2),半径为.
又点(1,2)到直线x+y-1=0的距离d==,
∴直线m被圆M截得的弦长等于2=2.]
考向4 直线与圆位置关系中的最值问题
[典例4] (2024·曲靖市会泽县期末)过直线x-2y+5=0上一点P向圆C:(x-1)2+(y+2)2=4作切线,切点为M,则|PM|的最小值为________.
4
4 [根据题意,圆C:(x-1)2+(y+2)2=4,其圆心C的坐标为(1,
-2),半径r=2,
圆心C到直线x-2y+5=0的距离d=
=2>2,
所以直线与圆相离,
因为△PCM为直角三角形,且PM⊥CM,
所以|PM|==4,
当且仅当PC与直线x-2y+5=0垂直时,等号成立,
所以|PM|的最小值为4.]
反思领悟 解答本题的关键是能够把所求线段长|PM|表示为圆心与直线上的点之间的距离的函数|PM|=的形式,然后利用求函数值域的方法求得最小值.
巩固迁移4 过直线x-y-m=0上一点P作圆M:(x-2)2+(y-3)2=1的两条切线,切点分别为A,B,若使得四边形PAMB的面积为的点P有两个,则实数m的取值范围为( )
A.(-5,3)
B.(-3,5)
C.(-∞,-5)∪(3,+∞)
D.(-∞,-3)∪(5,+∞)
√
A [由圆M:(x-2)2+(y-3)2=1可知,圆心M(2,3),半径为1,
所以|MA|=|MB|=1,
所以四边形PAMB的面积为S=|PA||MA|+|PB|·|MB|=|PA|=,
所以|PM|===2,
要使四边形PAMB的面积为的点P有两个,
则<2,解得-5
若两圆的半径分别为r1,r2,两圆的圆心距为d,则两圆的位置关系的判断方法如下:
外离 外切 相交 内切 内含
图形
量的关系 d>______ d=______ |r1-r2|<d<r1+r2 d=______ d<______
r1+r2
r1+r2
|r1-r2|
|r1-r2|
[常用结论]
1.两圆相交时公共弦所在直线的方程
设圆C1:x2+y2+D1x+E1y+F1=0,①
圆C2:x2+y2+D2x+E2y+F2=0,②
若两圆相交,则有一条公共弦,其公共弦所在直线方程由①-②所得,即(D1-D2)x+(E1-E2)y+(F1-F2)=0.
2.两个圆系方程
(1)过直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0交点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ∈R).
(2)过圆C1:x2+y2+D1x+E1y+F1=0和圆C2:x2+y2+D2x+E2y+F2=0交点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1)(该圆系不含圆C2,解题时,注意检验圆C2是否满足题意,以防漏解).
考向1 两圆位置关系的判断
[典例5] (2024·泊头市月考)已知圆C1:x2+(y-3)2=4与圆C2:x2+y2-6x+2y+1=0,则圆C1与圆C2的位置关系为( )
A.相交 B.外切
C.外离 D.内含
√
B [圆C1:x2+(y-3)2=4,圆心C1(0,3),半径r1=2,
圆C2:x2+y2-6x+2y+1=0可化为(x-3)2+(y+1)2=9,圆心C2(3,-1),半径r2=3,
则|C1C2|==5=2+3=r1+r2,
故圆C1与圆C2的位置关系为外切.故选B.]
反思领悟 判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.
巩固迁移5 (2025·北京市朝阳区模拟)已知圆E:(x-2)2+(y-4)2=25,圆F:(x-2)2+(y-2)2=1,则这两圆的位置关系为( )
A.内含 B.相切
C.相交 D.外离
√
A [圆E:(x-2)2+(y-4)2=25的圆心为E(2,4),半径r1=5,
圆F:(x-2)2+(y-2)2=1的圆心为F (2,2),半径r2=1,
因为圆心距|EF|==2,
且|EF|<|r1-r2|=4,所以两圆的位置关系为内含.
故选A.]
考向2 圆系方程
[典例6] (2024·沈阳市皇姑区期末)圆心在直线x-y-4=0上,且经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点的圆的方程为
( )
A.x2+y2-x+7y-32=0
B.x2+y2-x+7y-16=0
C.x2+y2-4x+4y+9=0
D.x2+y2-4x+4y-8=0
√
A [根据题意,要求圆经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点,
设其方程为(x2+y2+6x-4)+λ(x2+y2+6y-28)=0,
变形可得(1+λ)x2+(1+λ)y2+6x+6λy-4-28λ=0,
其圆心为,又由圆心在直线x-y-4=0上,
则有--4=0,解得λ=-7,
所以圆的方程为-6x2-6y2+6x-42y+192=0,
即x2+y2-x+7y-32=0,故选A.]
反思领悟 过两圆x2+y2+6x-4=0和x2+y2+6y-28=0交点的圆系方程为+y2+6y-28)=0.当λ=
-1时,这一方程为一次方程,两圆相交时,表示公共弦所在直线方程,两圆相切时,表示公切线所在直线方程.
巩固迁移6 (2025·太原市尖草坪区模拟)过点M(2,-1),且经过圆x2+y2-4x-4y+4=0与圆x2+y2-4=0的交点的圆的方程为( )
A.x2+y2+x+y-6=0
B.x2+y2+x-y-8=0
C.x2+y2-x+y-2=0
D.x2+y2-x-y-4=0
√
A [设经过圆x2+y2-4x-4y+4=0与圆x2+y2-4=0的交点的圆的方程为
(x2+y2-4x-4y+4)+λ(x2+y2-4)=0,
由题意将M的坐标代入可得(4+1-8+4+4)+λ(4+1-4)=0,
解得λ=-5,所以所求圆的方程为x2+y2+x+y-6=0,故选A.]
考向3 公切线、公共弦问题
[典例7] 已知两圆C1:x2+y2-2x+10y-24=0和C2:x2+y2+2x+2y-8=0.
(1)判断两圆公切线的条数;
(2)求公共弦所在的直线方程以及公共弦的长度.
[解] (1)两圆的标准方程分别为
C1:(x-1)2+(y+5)2=50,
C2:(x+1)2+(y+1)2=10,
则圆C1的圆心坐标为(1,-5),半径r1=5;
圆C2的圆心坐标为(-1,-1),半径r2=.
又|C1C2|=2,r1+r2=5,r1-r2=5,
所以r1-r2<|C1C2|
(2)将两圆方程相减,得公共弦所在直线方程为x-2y+4=0.
圆心C1到直线x-2y+4=0的距离d==3,
设公共弦长为2l,由勾股定理得=d2+l2,
得50=45+l2,解得l=,所以公共弦的长度为2l=2.
反思领悟 本例(1)中两圆相交,有两条公切线;本例(2),两圆方程作差消去x2,y2项得到x,y的二元一次方程即为公共弦所在直线方程;求公共弦长,常选其中一圆,由圆心到公共弦的距离d,半弦长l,半径r构成直角三角形,利用勾股定理求解.
巩固迁移7 (2025·金华市金东区模拟)圆C1:x2+y2=1与圆C2:x2+y2+2x-2y+1=0的公共弦长为( )
A. B.
C. D.1
√
B [两圆的圆心坐标分别为(0,0),(-1,1),半径均为1,故两圆的圆心距为,0<<2,故两圆相交,
∴圆x2+y2=1与圆x2+y2+2x-2y+1=0的公共弦所在直线的方程为
(x2+y2+2x-2y+1)-(x2+y2-1)=2x-2y+2=0,即x-y+1=0,
∵圆C1:x2+y2=1的圆心C1(0,0)到公共弦x-y+1=0的距离为d=
=,圆C1的半径r=1,∴公共弦长为2=.
故选B.]
随堂练习
√
1.(人教A版选择性必修第一册P91例1改编)圆(x-1)2+(y+2)2=6与直线2x+y-5=0的位置关系是( )
A.相切
B.相离
C.相交且直线过圆心
D.相交但直线不过圆心
D [由题意知圆心(1,-2)到直线2x+y-5=0的距离d==<,且2×1+(-2)-5≠0,所以直线与圆相交但不过圆心.故选D.]
2.(2024·上海市长宁区期末)圆A:x2+y2-8x+6y+16=0与圆B:x2+y2=64的位置关系是( )
A.相交 B.内切
C.相离 D.外切
√
B [把圆A:x2+y2-8x+6y+16=0化为标准方程得(x-4)2+(y+3)2=9,
∴圆心A的坐标为(4,-3),半径r=3,
由圆B:x2+y2=64,得到圆心B的坐标为(0,0),半径R=8,
两圆心间的距离d=|AB|=5,
∵8-3=5,即d=R-r,∴两圆的位置关系是内切.故选B.]
3.(2025·哈尔滨市香坊区模拟)已知圆C1:x2+y2=4,圆C2:x2+y2-4x-4y+4=0,两圆的公共弦所在直线的方程是( )
A.x+y+2=0 B.x+y-2=0
C.x+y+1=0 D.x+y-1=0
√
B [由圆C1:x2+y2=4,圆C2:x2+y2-4x-4y+4=0,
两式作差得4x+4y-4=4,即x+y-2=0,
所以两圆的公共弦所在直线的方程是x+y-2=0.故选B.]
4.(人教A版选择性必修第一册P92例2改编)圆x2+y2-4x=0在点P(1,)处的切线方程为_____________.
x-y+2=0 [圆的方程为(x-2)2+y2=4,圆心坐标为(2,0),半径为2,点P在圆上,所以点P与圆心连线的斜率为-,所以过点P
的切线的斜率为,所以切线方程为y-=(x-1),即x-y+
2=0.]
x-y+2=0
链接·2025高考试题
(2025·天津卷) l1:x-y+6=0与x轴交于点A,与y轴交于点B,与圆(x+1)2+(y-3)2=r2(r>0)交于C,D两点,|AB|=3|CD|,则r=________.
2
2 [对于直线l1:x-y+6=0,令x=0,得y=6,令y=0,得x=
-6,所以A(-6,0),B(0,6),所以|AB|=6.因为|AB|=3|CD|,所以|CD|=2.圆(x+1)2+(y-3)2=r2的圆心为(-1,3),圆心到直线l1的距离d==,所以r===2.]
【教用·备选题】
1.(2024·重庆市渝中区期末)已知圆C1:(x-a)2+(y-1)2=1与圆C2:(x-1)2+(y-3)2=4有且仅有2条公切线,则实数a的取值范围是
( )
A.(1-,1+) B.(1+,1+)
C.(-2,0) D.(1-,1+)
√
A [由圆C1:(x-a)2+(y-1)2=1与圆C2:(x-1)2+(y-3)2=4有且仅有2条公切线可知两圆的位置关系为相交,所以|r1-r2|<|C1C2|<r1
+r2,即1<<3,
平方得1<a2-2a+5<9,
解得1-
2.(2024·濮阳市南乐县月考)已知直线l:y=x+a与圆x2+y2=2和圆(x-4)2+y2=m2(m>0)都相切,则实数m的值为( )
A. B.2
C.3 D.或3
√
D [因为直线l:y=x+a与圆x2+y2=2相切,
所以=,解得a=±2,
因为直线l:y=x±2和圆(x-4)2+y2=m2(m>0)相切,
所以=m或=m,
解得m=3或m=,
故实数m的值为3或.
故选D.]
3.(2025·宜宾模拟)已知点P是直线x+y+3=0上一动点,过点P作圆C:(x+1)2+y2=1的两条切线,切点为A,B,则弦AB长度的最小值为( )
A.1 B.
C.2 D.2
√
B [易知当弦AB最小时,∠ACB最小,
则|PC|最小,
而|PC|的最小值为圆心C到直线x+y+3=0的距离,
即=,此时cos ∠ACP==,
则sin ∠ACP===|AB|,
解得|AB|=.故选B.]
4.(2024·绵阳市开学考试)已知A(0,-2),B(2,0),点P为圆C:x2+y2-2x-8y+13=0上任意一点,则△PAB面积的最大值为( )
A.5 B.5-2
C. D.5+2
√
D [圆x2+y2-2x-8y+13=0的圆心C(1,4),半径r=2,
直线AB的方程为y=x-2,
于是点C到直线AB:x-y-2=0的距离
d==,而点P在圆C上,
因此点P到直线AB距离的最大值为+2,
又|AB|==2,所以△PAB面积的最大值为S=×2=5+2.故选D.]
5.(2024·郴州期末)若直线l:kx-y+2-2k=0与曲线C:y=有两个不同的交点,则实数k的取值范围是________.
[由题意可得直线l:kx-y+2-2k=0即y=k(x-2)+2,
所以直线l恒过定点A(2,2),
曲线C:y=为以(0,0)为圆心,
2为半径的上半圆(包含x轴部分),
它们的图象如图所示.
当直线l过点(-2,0)时,它们有两个交点,此时k==,
当直线l与上半部分圆相切时,有一个交点,此时k=0,
由图象可知,若直线l与曲线C有两个不同的交点,则0
课后习题(五十三) 直线与圆、圆与圆的位置关系
1.(人教A版选择性必修第一册P92例2改编)由直线x-y+4=0上一点P向圆C:(x-1)2+(y-1)2=1引切线,则切线长的最小值为( )
A. B.3
C.2 D.2-1
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [圆(x-1)2+(y-1)2=1的圆心C(1,1),半径为1,由直线x-y+4=0上一点P向圆(x-1)2+(y-1)2=1引切线,设切点为M,连接PC,MC(图略),则|PM|==,要使切线长最小,则|PC|最小,而|PC|的最小值等于圆心C到直线x-y+4=0的距离,故|PC|min==2,
故切线长的最小值为=.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教B版选择性必修第一册P120探索与研究改编)圆x2-4x+y2=0与圆x2+y2+4x+3=0的公切线共有( )
A.1条 B.2条
C.3条 D.4条
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由x2-4x+y2=0,得(x-2)2+y2=22,则圆心坐标为(2,0),半径为2;由x2+y2+4x+3=0,得(x+2)2+y2=12,则圆心坐标为
(-2,0),半径为1.
故两圆的圆心距为4,半径之和为3,
因为4>3,所以两圆的位置关系是外离,故两圆的公切线共有4条.
故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(多选)(人教A版选择性必修第一册P98练习T2改编)已知圆O1:x2+y2-2x=0和圆O2:x2+y2+2x-8y=0的交点为A,B,则下列结论正确的是( )
A.直线AB的方程为x-2y=0
B.|AB|=
C.线段AB的垂直平分线方程为2x+y-2=0
D.若点P为圆O1上的一个动点,则点P到直线AB的距离的最大值为+1
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ACD [根据题意,由x2+y2-2x=0,得(x-1)2+y2=1,则圆心O1(1,0),半径r=1,由x2+y2+2x-8y=0,得(x+1)2+(y-4)2=17,则圆心O2(-1,4),半径R=.
对于A,联立得x-2y=0,
即直线AB的方程为x-2y=0,A正确;对于B,圆心O1到直线AB的
距离d==,则|AB|=2×=,B错误;
对于C,线段AB的垂直平分线即直线O1O2,由O1(1,0),O2(-1,4),易得直线O1O2的方程为2x+y-2=0,C正确;对于D,由圆心
O1到直线AB的距离d=,知点P到直线AB的距离的最大值为+
1,D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第一册P92例2改编)过点A(3,5)作圆O:x2+y2-2x-4y+1=0的切线,则切线的方程为_____________________
____.
5x-12y+45=0或x-3
=0
题号
1
3
5
2
4
6
8
7
9
10
11
12
5x-12y+45=0或x-3=0 [圆x2+y2-2x-4y+1=0化为标准方程得(x-1)2+(y-2)2=4,则圆心O(1,2),半径为2,
因为|OA|==>2,所以点A(3,5)在圆外.显然,当切线斜率不存在时,直线与圆相切,即切线方程为x-3=0;当切线斜率存在时,设所求切线方程为y-5=k(x-3),即kx-y+5-3k=0.又圆心为(1,2),半径r=2,而圆心到切线的距离d==2,即|3-2k|=2,解得k=,此时直线方程为5x-12y+45=0.
故所求切线方程为5x-12y+45=0或x-3=0.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2025·唐山模拟)已知直线l:x-y+2=0,圆C:x2+y2=r2(r>0),若圆C上恰有三个点到直线l的距离等于,则r=( )
A.2 B.4
C.2 D.8
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [圆心C(0,0),则点C到直线l的距离d==,又因为圆C上恰有三个点到直线l的距离为,所以圆心到直线l的距离d=,
即r=2d=2.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·重庆市沙坪坝区期末)过点P(-1,1)的直线l与圆C:x2+y2+4x-2=0交于A,B两点,则|AB|的最小值为( )
A.2 B.
C.4 D.2
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [圆C的标准方程为(x+2)2+y2=6,圆心C(-2,0),半径r=,
因为(-1+2)2+12<6,所以点P(-1,1)在圆C内,
设圆心C到直线l的距离为d,则|AB|=2,
当d=|CP|,即CP⊥l时,|AB|取得最小值,
因为|CP|==,
所以|AB|的最小值为2=4.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(多选)(2025·菏泽市牡丹区模拟)已知直线l:x+my-m+2=0,圆C:(x-1)2+(y-2)2=5,则下列说法正确的是( )
A.直线l恒过定点(-2,1)
B.直线l与圆C相交
C.当直线l平分圆C时,m=-3
D.当点C到直线l的距离最大时,m=
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ACD [对于A,l:x+my-m+2=0,即x+2+m(y-1)=0,
令y-1=0,有y=1,x=-2,所以直线l恒过定点P(-2,1),故A正确;
对于B,圆C:(x-1)2+(y-2)2=5的圆心C(1,2),半径r=,
点C(1,2)到直线l:x+my-m+2=0的距离为d=,
从而d2-r2=-5==,
取m=2,则此时有d=r,即圆C与直线l相切,故B错误;
对于C,当直线l平分圆C时,点C(1,2)在直线l:x+my-m+2=0上,
即1+2m-m+2=0成立,解得m=-3,故C正确;
对于D,点C到直线l的距离满足d≤|PC|,当且仅当PC⊥l时,等号成立,
而PC的斜率为k==,
所以当等号成立时有·=-1,解得m=,故D正确.
故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·连云港期末)已知圆C:x2+y2-4y+2=0,则下列说法正确的有( )
A.圆C关于直线x-y=0对称的圆的方程为(x-2)2+y2=2
B.直线x-y+1=0被圆C截得的弦长为
C.若圆C上有四个点到直线x-y+m=0的距离等于,则m的取值范围
是(1,3)
D.若点P(x,y)是圆C上的动点,则x2+y2的取值范围是[2-,2+]
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AC [A项,圆C:x2+y2-4y+2=0,即为x2+(y-2)2=2,圆心为(0,2),半径为,
因为(0,2)关于直线x-y=0对称的坐标为(2,0),则圆C关于直线x-y=0的对称圆的方程为(x-2)2+y2=2,故A正确;
B项,圆心C(0,2)到直线x-y+1=0的距离为,
则所求弦长为2=,故B错误;
题号
1
3
5
2
4
6
8
7
9
10
11
12
C项,由题意有圆心C到直线x-y+m=0的距离小于r-,
即<=,
∴|m-2|<1,∴1<m<3,
则m的取值范围是(1,3),故C正确;
D项,根据圆的标准方程,可设x=cos α,y=sin α+2,
x2+y2=2sin2α+2sin2α+4+4sinα=6+4sin α,
则x2+y2的取值范围是[6-4,6+4],故D错误.
故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·淮北一模)已知圆O:x2+y2=9与圆C:x2+y2-4x-6y+9=0交于A,B两点,则直线AB的方程为_____________;△ABC的面积为________.
2x+3y-9=0
题号
1
3
5
2
4
6
8
7
9
10
11
12
2x+3y-9=0 [两圆的方程相减得4x+6y=18,化简得2x+3y
-9=0,故直线AB的方程为2x+3y-9=0.圆C:x2+y2-4x-6y+9=0变形得到(x-2)2+(y-3)2=4,圆心C(2,3),半径为2,
故圆心C(2,3)到直线AB的距离为d==,
则|AB|=2×=,
故△ABC的面积为|AB|·d==.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·南京市雨花台区三模)已知圆O:x2+y2=2,过点M(1,3)的直线l交圆O于A,B两点,且|AB|=2,则直线l的方程为___________________.
x=1或4x-3y+5=0 [当直线l的斜率不存在时,l的方程为x=1,
由可得或
所以|1-(-1)|=2=|AB|,符合题意;
x=1或4x-3y+5=0
题号
1
3
5
2
4
6
8
7
9
10
11
12
当直线l的斜率存在时,设l的方程为y-3=k(x-1),
因为|AB|=2,所以圆心(0,0)到直线l的距离d=,
由+d2=2,得k=,所以直线l的方程为y-3=(x-1),
则直线l的方程为x=1或4x-3y+5=0.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·江门市新会区月考)已知圆C的方程为x2+y2-2x-4y+2m=0.
(1)求实数m的取值范围;
(2)若直线x-2y-1=0与圆C相切,求实数m的值;
(3)若圆C与圆O:x2+y2=1相切,求实数m的值.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)x2+y2-2x-4y+2m=0,
可化为(x-1)2+(y-2)2=5-2m,
所以5-2m>0 m<,故m的取值范围为.
(2)由(1)知,圆心C(1,2),半径r=,
因为圆(x-1)2+(y-2)2=5-2m和直线x-2y-1=0相切,
所以=,解得m=.
(3)因为圆O:x2+y2=1与圆C相切,
所以|OC|=1+=或|OC|=|-1|=,
解得m=<或m=-<,
故实数m的值是或-.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·吉林期末)已知动点P与两个定点A(1,0),B(4,0)的距离的比是2.
(1)求动点P的轨迹C的方程;
(2)直线l过点(2,1),且被曲线C截得的弦长为2,求直线l的方程.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)设点P(x,y),
∵动点P与两个定点A(1,0),B(4,0)的距离的比是2,
∴=2,即|PA|=2|PB|,
则=2,化简得x2+y2-10x+21=0,
所以动点P的轨迹C的方程为(x-5)2+y2=4.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)由(1)可知点P的轨迹C是以(5,0)为圆心,2为半径的圆,
∵直线l被曲线C截得的弦长为2,
∴圆心(5,0)到直线l的距离d==1.
①当直线l的斜率不存在时,直线l的方程为x=2,此时圆心到直线l的距离是3,不符合题意;
②当直线l的斜率存在时,设直线l的方程为y-1=k(x-2),即kx-y-2k+1=0,
题号
1
3
5
2
4
6
8
7
9
10
11
12
所以圆心(5,0)到直线l的距离d==1,
化简得9k2+6k+1=k2+1,解得k=0或k=-,
此时直线l的方程为y=1或3x+4y-10=0.
综上,直线l的方程是y=1或3x+4y-10=0.
谢 谢 !
同课章节目录
