《高考快车道》2026版高三一轮总复习数学(基础版)98 第九章 第1课时 两个计数原理 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)98 第九章 第1课时 两个计数原理 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-12-04 00:00:00 | ||
图片预览




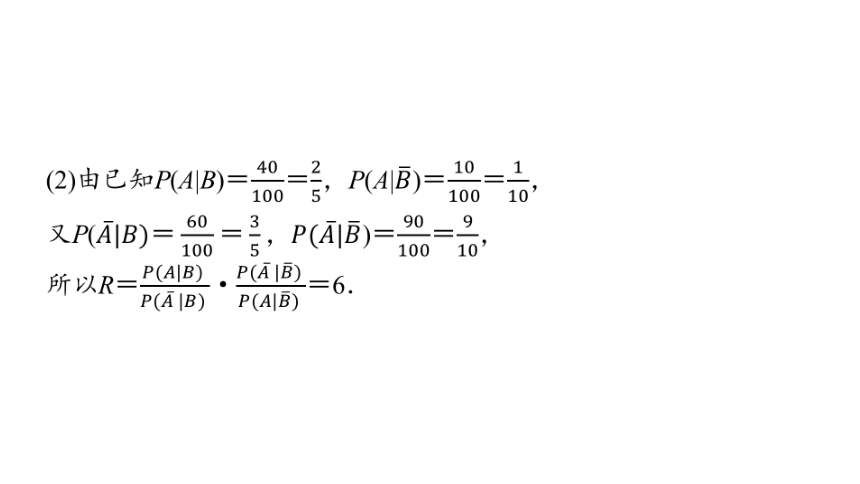




文档简介
(共78张PPT)
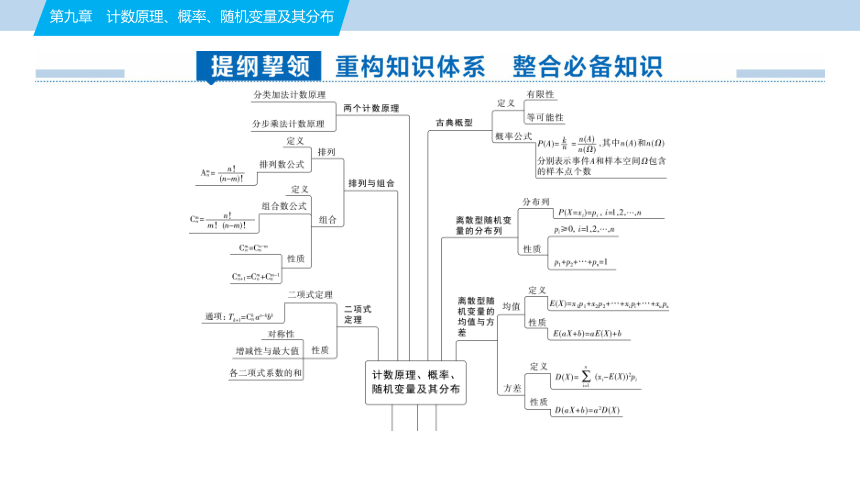
第九章 计数原理、概率、随机变量及其分布
第九章 计数原理、概率、随机变量及其分布
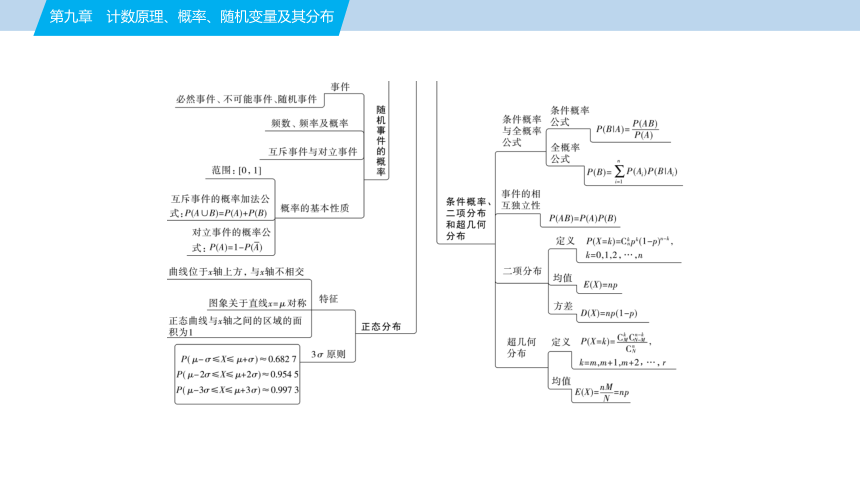
第九章 计数原理、概率、随机变量及其分布
条件概率是新教材中增加的内容,并增加了与条件概率相关的全概率公式和贝叶斯公式,在近年高考中条件概率考查频率较高,在今后的高考中值得期待.
第九章 计数原理、概率、随机变量及其分布
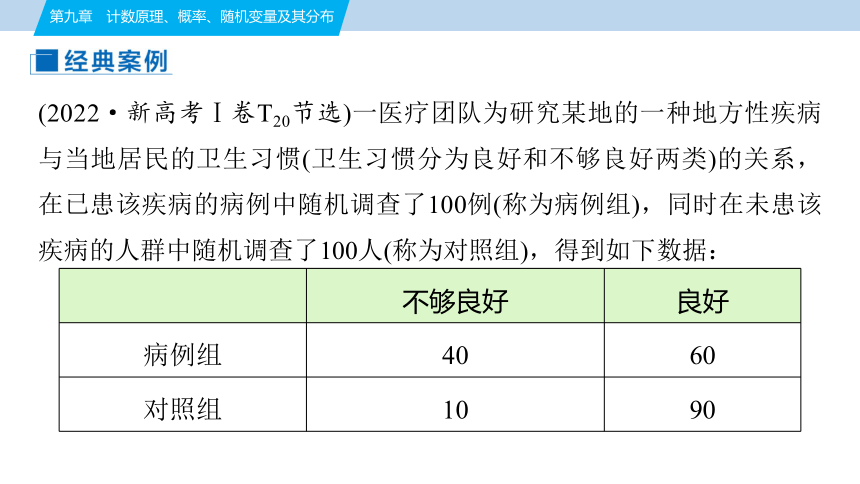
(2022·新高考Ⅰ卷T20节选)一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:
第九章 计数原理、概率、随机变量及其分布
不够良好 良好
病例组 40 60
对照组 10 90
从该地的人群中任选一人,A表示事件“选到的人卫生习惯不够良
好”,B表示事件“选到的人患有该疾病”,与的比值
是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.
(1)证明:R=·;
(2)利用该调查数据,给出P(A|B),P(A|)的估计值,并利用(1)的结果给出R的估计值.
第九章 计数原理、概率、随机变量及其分布
[阅读与思考] (1)证明:R==,
由题意知,证明=即可,
左边==,
右边==.
左边=右边,故R=·.
(2)由已知P(A|B)==,P(A|)==,
又P()==,
所以R=·=6.
本题参照人教A版教材选择性必修第三册P53习题7.1T10命制.教材习
题和高考题都是利用条件概率公式P(B|A)=进行推理并证明指
定结论,高考题的难度略高于教材习题,考查了逻辑推理、数学运算等学科核心素养,难度中等.
第九章 计数原理、概率、随机变量及其分布
必修1 中国特色社会主义
试题评价:本题的医疗团队课题研究问题有着现实的背景,以医疗团队研究地方性疾病与居民卫生习惯的关系为情境素材,引导学生用所学知识解决社会实践中的问题,属于生活实践情境.
附:(人教A版选择性必修第二册P53习题7.1T10)证明:当P(AB)>0时,P(ABC)=P(A)P(B|A)·P(C|AB).据此你能发现计算P(A1A2…An)的公式吗?
第九章 计数原理、概率、随机变量及其分布
第1课时 两个计数原理
[考试要求] 1.理解分类加法计数原理和分步乘法计数原理.
2.会用两个计数原理分析和解决一些简单的实际问题.
考点一 分类加法计数原理
1.分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=______种不同的方法.
2.分类加法计数原理的推广:完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有N=____________________种不同的方法.
m+n
m1+m2+…+mn
[典例1] (1)(2024·天津南开区期末)甲、乙、丙三人踢毽子,互相传递,每人每次只能踢一下,若由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )
A.4种 B.5种 C.6种 D.12种
(2)椭圆=1(m>0,n>0)的焦点在x轴上,且m∈{1,2,3,4,5},n∈{1,2,3,4,5,6,7},则这样的椭圆的个数为( )
A.10 B.12 C.20 D.35
√
√
(1)C (2)A [(1)当开始甲将球传给乙时,经过4次传球后,球正好回到甲手中的传球方式有3种:
甲→乙→甲→丙→甲,甲→乙→甲→乙→甲,甲→乙→丙→乙→甲;
当开始甲将球传给丙时,经过4次传球后,球正好回到甲手中的传球方式有3种:
甲→丙→乙→丙→甲,甲→丙→甲→丙→甲,甲→丙→甲→乙→甲;
所以不同的传球方式有3+3=6(种).故选C.
(2)因为焦点在x轴上,所以m>n,以m的值为标准分类,由分类加法计数原理,可分为四类,第一类:当m=5时,n有4种选择;第二类:当m=4时,n有3种选择;第三类:当m=3时,n有2种选择;第四类:当m=2时,n有1种选择.故符合条件的椭圆共有10个.]
【教用·备选题】
母题探究 在本例(2)中,若m∈{1,2,…,k},n∈{1,2,…,k}(k∈N*),其他条件不变,这样的椭圆有多少个?
[解] 因为m>n,当m=k时,n=1,2,…,k-1;
当m=k-1时,n=1,2,…,k-2;
……
当m=3时,n=1,2;当m=2时,n=1.
所以共有1+2+…+(k-1)=(个)椭圆.
反思领悟 本例(1)要注意不能漏数,还要注意是否重复(多数);本例(2)要注意分类标准要统一,不能遗漏.
巩固迁移1 (人教A版选择性必修第三册P5例3改编)某影城有一些电影新上映,其中有2部科幻片、3部文艺片、2部喜剧片,小明从中任选1部电影观看,不同的选法种数为( )
A.2+3+2=7 B.1+1+1=3
C.2×3×2=12 D.(23)2=64
√
A [由分类加法计数原理可知,不同的选法种数为2+3+2=7.故选A.]
考点二 分步乘法计数原理
1.分步乘法计数原理:完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=______种不同的方法.
2.分步乘法计数原理的推广:完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=____________________种不同的方法.
m×n
m1×m2×…×mn
[典例2] (多选)(2024·合肥调研)现安排高二年级A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名同学只能选择一个工厂,且允许多人选择同一个工厂,则下列说法正确的是( )
A.共有43种不同的安排方法
B.若甲工厂必须有同学去,则不同的安排方法有37种
C.若A同学必须去甲工厂,则不同的安排方法有12种
D.若三名同学所选工厂各不相同,则不同的安排方法有24种
√
√
√
ABD [对于A,A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名学生有4种选法,则三名学生有4×4×4=43(种)选法,故A正确;
对于B,三人到四个工厂,有43=64(种)情况,其中甲工厂没有人去,即三人全部到乙、丙、丁三个工厂的情况有33=27(种),则甲工厂必须有同学去的安排方法有64—27=37(种),故B正确;
对于C,若同学A必须去甲工厂,剩下2名同学安排到4个工厂即可,有42=16(种)安排方法,故C错误;
对于D,若三名同学所选工厂各不相同,有4×3×2=24(种)安排方法,故D正确.]
反思领悟 利用分步乘法计数原理解题的策略
(1)明确题目中的“完成这件事”是什么,确定完成这件事需要几个步骤,且每步都是独立的.
(2)将这件事划分成几个步骤来完成,各步骤之间有一定的连续性,只有当所有步骤都完成了,整个事件才算完成.
巩固迁移2 (1)(2024·济南期末)大明湖是济南三大名胜之一,素有“泉城明珠”之美誉,自2017年1月1日起全面向社会免费开放.景区有东南西北4个大门,每个大门进去都有不同景致,小明从一个大门进,另一个大门出,则不同进出方式的种数为( )
A.7 B.8 C.12 D.16
(2)将4个不同的小球放入3个不同的盒子中,且每个盒子最多只能装3个球,则不同的放法有( )
A.60种 B.64种 C.78种 D.81种
√
√
(1)C (2)C [(1)根据题意,景区有4个大门,从一个大门进,有4种走法,
另一个大门出,有3种走法,则有4×3=12(种)不同的走法.故选C.
(2)不考虑每个盒子最多只能装3个球,有34种放法.
若将4个球放入同一个盒子中,有3种放法.
故不同的放法有34-3=78(种).故选C.]
考点三 两个计数原理的综合应用
两个计数原理的区别与联系
分类加法计数原理 分步乘法计数原理
相同点 用来计算完成一件事的方法种数
不同点 分类、相加 分步、相乘
每类方案中的每一种方法都能独立完成这件事 每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
注意点 类类独立,不重不漏 步步相依,缺一不可
提醒:分类加法计数原理与分步乘法计数原理是解决排列组合问题的基础,并贯穿其始终.
(1)分类加法计数原理中,完成一件事的方法属于其中一类,并且只属于其中一类.
(2)分步乘法计数原理中,各个步骤中的方法相互依存,步与步之间“相互独立,分步完成”.
考向1 与数字有关的问题
[典例3] (2024·洛阳期中)用0,1,2,3,4这五个数字组成没有重复数字的三位数,其中奇数共有( )
A.48个 B.24个
C.18个 D.12个
√
C [根据题意,三位数的个位数字必须为1或3,有2种情况,
百位数字不能为0,有3种情况,
十位数字在剩下的3个数字中任选1个,有3种情况,
则共有2×3×3=18(种)情况,即有18个符合题意的三位奇数.
故选C.]
反思领悟 本例中,要完成的“一件事”为组成无重复数字的三位奇数,所以百位数字不能为0,个位数字必须是奇数,因此应先分类、再分步.
巩固迁移3 从数字1,2,3,4中取出3个数字(允许重复)组成三位数,各位数字之和等于6,则这样的三位数的个数为( )
A.7 B.9
C.10 D.13
√
C [其中各位数字之和等于6的三位数可分为以下情形:
①由1,1,4三个数字组成的三位数:114,141,411,共3个;
②由1,2,3三个数字组成的三位数:123,132,213,231,312,321,共6个;
③由2,2,2三个数字可以组成1个三位数,即222.
共有3+6+1=10(个).]
考向2 与几何有关的问题
[典例4] 如果一条直线与一个平面垂直,那么称此直线与该平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18
C.24 D.36
√
D [分类讨论:第一类,对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有2×12=24(个);第二类,对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有2×6=12(个);第三类,对于每一条体对角线,没有符合题意的平面与之构成“正交线面对”.所以正方体中“正交线面对”共有24+12=36(个).故选D.]
反思领悟 解决本例的关键是画出正方体,弄清楚正方体中的垂直关系,合理分类将问题简化.
巩固迁移4 如果一条直线与一个平面平行,那么称此直线与平面构成一个“平行线面组”.在一个长方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是( )
A.60 B.48
C.36 D.24
√
B [长方体的6个表面构成的“平行线面组”的个数为6×6=36,另含4个顶点的6个面(非表面)构成的“平行线面组”的个数为6×2=12,故符合条件的“平行线面组”的个数是36+12=48.]
考向3 涂色、种植问题
[典例5] 中国是世界上最早发明雨伞的国家,伞是中国劳动人民一个重要的创造.如图所示的雨伞,其伞面被伞骨分成8个区域,每个区域分别印有数字1,2,3,…,8,现准备给该伞面的每个区域涂色,要求每个区域涂一种颜色,相邻两个区域所涂颜色不能相同,对称的两个区域(如区域1与区域5)所涂颜色相同.若有7种不同颜色的颜料可供选择,则不同的涂色方案有( )
A.1 050种 B.1 260种
C.1 302种 D.1 512种
√
C [由题意可得,只需确定区域1,2,3,4的颜色,即可确定整个伞面的涂色.
先涂区域1,有7种选择;再涂区域2,有6种选择.
当区域3与区域1涂的颜色不同时,区域3有5种选择,剩下的区域4有5种选择.
当区域3与区域1涂的颜色相同时,剩下的区域4有6种选择.
故不同的涂色方案有7×6×(5×5+1×6)=1 302(种).]
反思领悟 涂色问题,可按颜色的种数用分类加法计数原理分析,也可按不同的区域用分步乘法计数原理分析.
巩固迁移5 某学校有一块绿化用地,其形状如图所示.为了让效果更美观,要求在四个区域内种植花卉,且相邻区域花卉颜色不同.现有五种不同颜色的花卉可供选择,则不同的种植方案共有________种.(用数字作答)
180
180 [先在A中种植,有5种不同的种植方法,再在B中种植,有4种不同的种植方法,再在C中种植,有3种不同的种植方法,最后在D中种植,有3种不同的种植方法,
所以不同的种植方案共有5×4×3×3=180(种).]
随堂练习
√
1.(2025·广东汕头模拟)电脑调色板有红、绿、蓝三种基本颜色,每种颜色的色号均为0~255.在电脑上绘画可以分别从三种颜色的色号中各选一个配成一种颜色,那么在电脑上可配成的颜色种数为( )
A.2563 B.27
C.2553 D.6
A [分3步取色,第一、第二、第三次都有256种取法,根据分步乘法计数原理得,共可配成256×256×256=2563(种)颜色.]
2.(人教A版选择性必修第三册P5练习T1(1))一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这项工作,不同选法的种数是________.
9 [因为一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,所以从中选出1人来完成这项工作,不同选法的种数是5+4=9.]
9
3.(人教A版选择性必修第三册P5练习T1(2))从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同路线的条数是________.
6 [因为从A村去B村的道路有3条,从B村去C村的道路有2条,所以从A村经B村去C村,不同路线的条数是3×2=6.]
6
4.一个圆的圆周上均匀分布6个点,在这些点与圆心共7个点中,任取3个点,这3个点能构成不同的等边三角形的个数为________.
8
8 [如图1,由圆上相邻两个点和圆心可构成等边三角形,共有6个;
如图2,由圆上相间隔的三点可构成等边三角形,共有2个,
所以在这7个点中,任取3个点,这3个点能构成不同的等边三角形的个数为6+2=8. ]
【教用·备选题】
1.(2024·广州越秀区期末)学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,不同的选法种数为( )
A.10 B.15
C.60 D.125
√
D [由题意可分三步:甲同学有5种选法,乙同学有5种选法,丙同学有5种选法,
共5×5×5=125(种).故选D.]
2.(多选)(2024·宿迁期末)下列说法中正确的有( )
A.4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有43种报名方法
B.4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有34种报名方法
C.4名同学争夺跑步、跳高、跳远三项冠军(每项冠军只允许一人获得),共有43种可能结果
D.4名同学争夺跑步、跳高、跳远三项冠军(每项冠军只允许一人获得),共有34种可能结果
√
√
BC [对于A、B,4名同学选报跑步、跳高、跳远三个项目,每人报一项,每人都有3种选择,共有34种报名方法,所以A错误,B正确;
对于C、D,4名同学争夺跑步、跳高、跳远三项冠军(每项冠军只允许一人获得),每个冠军有4种可能,共有43种可能结果,所以C正确,D错误.故选BC.]
3.(2025·江西南昌模拟)四面体的顶点和各棱的中点共10个点.在这10个点中取4个不共面的点,则不同的取法种数为( )
A.141 B.144
C.150 D.155
√
A [从10个点中任取4个点有种取法,其中4点共面的情况有三类.
第一类,取出的4个点位于四面体的同一个面上,有种;
第二类,取任一条棱上的3个点及该棱所对棱的中点,这4点共面,有6种;
第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个顶点共面,有3种.
以上三类情况不合要求应减掉,
∴不同的取法共有-6-3=141(种).
故选A.]
4.(2024·北京朝阳区期末)用四种颜色给正四棱锥V-ABCD的五个顶点涂色,要求每个顶点涂一种颜色,且每条棱的两个顶点涂不同颜色,则不同的涂法有( )
A.72种 B.36种
C.12种 D.60种
√
A [①当用2种颜色涂A,B,C,D时,则A,C涂色相同,B,D涂色相同,共有=12(种)涂色方法,则涂V有2种涂色方法,
即给正四棱锥V-ABCD的五个顶点涂色,
共12×2=24(种)涂色方法;
②当用3种颜色涂A,B,C,D时,则A,
C涂色相同,B,D涂色不相同,或A,C涂色不相同,B,D涂色相同,共有=48(种)涂色方法,则涂V有1种涂色方法,
即给正四棱锥V-ABCD的五个顶点涂色,共48×1=48(种)涂色方法;
由①②得,不同的涂法有24+48=72(种).故选A.]
5.(2024·眉山仁寿县月考)已知0,1,2,3,4,5这六个数字.
(1)可以组成多少个无重复数字的三位数?
(2)可以组成多少个无重复数字的三位奇数?
(3)可以组成多少个无重复数字的小于1 000的自然数?
(4)可以组成多少个无重复数字的大于3 000且小于5 421的四位数?
[解] (1)分3步:
①先选百位数字有5种选法,
②十位数字有5种选法,
③个位数字有4种选法,
由分步乘法计数原理知所求三位数共有5×5×4=100(个).
(2)分3步:
①先选个位数字,由于组成的三位数是奇数,因此有3种选法,
②再选百位数字有4种选法,
③十位数字也有4种选法,
由分步乘法计数原理知所求三位数共有3×4×4=48(个).
(3)分3类:
①一位数,共有6个,
②两位数,先选十位数字,有5种选法,再选个位数字也有5种选法,共有5×5=25(个),
③三位数,先选百位数字,有5种选法,再选十位数字也有5种选法,再选个位数字,有4种选法,共有5×5×4=100(个),
因此,比1 000小的自然数共有6+25+100=131(个).
(4)分4类:
①千位数字为3或4时,后面三个数位上可随便选择,此时共有2×5×4×3=120(个),
②千位数字为5,百位数字为0,1,2,3之一时,共有4×4×3=48(个),
③千位数字为5,百位数字是4,十位数字为0,1之一时,共有2×3=6(个),
④5 420也满足条件.
故所求四位数共有120+48+6+1=175(个).
课后习题(五十九) 两个计数原理
1.(人教A版选择性必修第三册P11练习T2改编)在所有的两位数中,个位数字大于十位数字的两位数的个数是( )
A.18 B.36
C.72 D.48
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [法一:按十位上的数字分别是1,2,3,4,5,6,7,8分成八类,在每一类中满足条件的两位数分别有8个、7个、6个、5个、4个、3个、2个、1个.由分类加法计数原理知,满足条件的两位数的个数是8+7+6+5+4+3+2+1=36.
法二:按个位上的数字分别是2,3,4,5,6,7,8,9分成八类,在每一类中满足条件的两位数分别有1个、2个、3个、4个、5个、6个、7个、8个.由分类加法计数原理知,满足条件的两位数的个数是1+2+3+4+5+6+7+8=36.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版选择性必修第三册P27习题6.2T17改编)如图,用4种不同的颜色把图中A,B,C,D四块区域区分开,若相邻区域不能涂同一种颜色,则不同的涂法共有( )
A.144种 B.73种
C.48种 D.32种
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [第一步,给A区域涂色,有4种涂法;第二步,给B区域涂色,有3种涂法;第三步,给C区域涂色,有2种涂法;第四步,给D区域涂色,有2种涂法.所以共有4×3×2×2=48(种)涂法.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教A版选择性必修第三册P8例7改编)如图,将一条电路从A处到B处接通时,可以有________条不同的线路(每条线路仅含一条通路).
9
题号
1
3
5
2
4
6
8
7
9
10
11
12
9 [依题意,按上、中、下三种线路分为三类,上线路有2条,中线路有1条,下线路有2×3=6(条).根据分类加法计数原理知,共有2+1+6=9(条).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第三册P12习题6.1T8改编)5名学生报名参加四项体育比赛,每人限报一项,则不同的报名方法的种数为________.5名学生争夺四项比赛的冠军(冠军不并列),则获得冠军的可能性有________种.(用数字作答)
1 024 625 [5名学生参加四项体育比赛,每人限报一项,可逐个学生落实,每名学生有4种报名方法,共有45=1 024(种)不同的报名方法.5名学生争夺四项比赛的冠军,可对4个冠军逐一落实,每个冠军有5种获得的可能性,共有54=625(种)获得冠军的可能性.]
1 024
625
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·河池月考)一个4层书架上,分别放置科普类读物10本、人文类读物10本、自然类读物9本、漫画类读物8本,每本书各不相同,从中取出1本,则不同的取法共有( )
A.4种 B.7 200种
C.27种 D.37种
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由题意知,每本书各不相同,从中取出1本,共有37本书,所以不同的取法共有37种.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·临洮县期末)从由1,2,3,4,5组成的没有重复数字的两位数中任取一个,则这个两位数大于40的个数是( )
A.6 B.8
C.10 D.12
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [因为这个两位数大于40,
所以选取十位数为4或5,个位数不重复,则在剩余的4个数字里选择1个,
这个两位数大于40的个数为2×4=8.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·北京石景山区开学考试)首位数字是1,且恰有两个数字相同的四位数共有( )
A.216个 B.252个
C.324个 D.432个
√
D [①两个相同数字是1,一共有3×9×8种组合;
②两个相同数字不是1,同样一共有3×9×8种组合.
所以这样的四位数有2×3×9×8=432(个).故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·重庆万州区月考)设从东、西、南、北四面通往山顶的路分别有2,3,3,4条,现要从一面上山,从剩余三面中的任意一面下山,则下列结论正确的是( )
A.从东面上山有20种走法
B.从西面上山有27种走法
C.从南面上山有30种走法
D.从北面上山有32种走法
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [对于A,若从东面上山,上山的路有2条,下山的路有3+3+4=10(条),则有2×10=20(条),A正确;
对于B,若从西面上山,上山的路有3条,下山的路有2+3+4=9(条),则有3×9=27(条),B正确;
对于C,若从南面上山,上山的路有3条,下山的路有2+3+4=9(条),则有3×9=27(条),C错误;
对于D,若从北面上山,上山的路有4条,下山的路有2+3+3=8(条),则有4×8=32(条),D正确.
故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·临汾调考)如图所示的五个区域中,现有四种颜色可供选择,要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法有( )
A.24种 B.48种
C.72种 D.96种
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [分两种情况:
①A,C不同色,先涂A有4种,C有3种,E有2种,B,D有1种,有4×3×2×1=24(种);
②A,C同色,先涂A,C有4种,再涂E有3种,B,D各有2种,有4×3×2×2=48(种).
故不同的涂色方法有48+24=72(种).故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·杭州调研)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )
A.243 B.252
C.261 D.279
√
B [0,1,…,9共能组成9×10×10=900(个)三位数,
其中无重复数字的三位数有9×9×8=648(个),
故有重复数字的三位数有900-648=252(个).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·乐山期末)由数字2,3,4,5可组成______个三位数(各位上数字可重复,用数字作答).
64 [由题意,百位、十位和个位上的数字均有4种选法,
故由数字2,3,4,5可以组成4×4×4=64(个)三位数.]
64
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·连云港赣榆区月考)从0,1,2,3,4五个数字中选出3个数字组成一个三位数.
(1)可以组成多少个三位数?
(2)可以组成多少个无重复数字的三位数?
(3)可以组成多少个无重复数字的三位偶数?
[解] (1)三位数的首位不能为0,但可以有重复数字,首先考虑首位的排法,除0外共有4种方法,第二、三位可以排0,因此,根据分步乘法计数原理共有4×5×5=100(个).
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)三位数的首位不能为0,首先考虑首位的排法,除0外共有4种方法,第二位可以排0,
除首位排的数字外共有4种方法,第三位除前两位排的数字外共有3种方法,
因此,根据分步乘法计数原理共有4×4×3=48(个).
(3)偶数末位数字可取0,2,4,因此,可以分两类:
一类是末位数字是0,则有4×3=12(种)排法;
一类是末位数字不是0,则末位有2种排法,即2或4,再排首位,因0不能在首位,
所以有3种排法,十位有3种排法,因此有2×3×3=18(种)排法.
因此有12+18=30(种)排法.即可以排成30个无重复数字的三位偶数.
谢 谢 !
第九章 计数原理、概率、随机变量及其分布
第九章 计数原理、概率、随机变量及其分布
第九章 计数原理、概率、随机变量及其分布
条件概率是新教材中增加的内容,并增加了与条件概率相关的全概率公式和贝叶斯公式,在近年高考中条件概率考查频率较高,在今后的高考中值得期待.
第九章 计数原理、概率、随机变量及其分布
(2022·新高考Ⅰ卷T20节选)一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:
第九章 计数原理、概率、随机变量及其分布
不够良好 良好
病例组 40 60
对照组 10 90
从该地的人群中任选一人,A表示事件“选到的人卫生习惯不够良
好”,B表示事件“选到的人患有该疾病”,与的比值
是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为R.
(1)证明:R=·;
(2)利用该调查数据,给出P(A|B),P(A|)的估计值,并利用(1)的结果给出R的估计值.
第九章 计数原理、概率、随机变量及其分布
[阅读与思考] (1)证明:R==,
由题意知,证明=即可,
左边==,
右边==.
左边=右边,故R=·.
(2)由已知P(A|B)==,P(A|)==,
又P()==,
所以R=·=6.
本题参照人教A版教材选择性必修第三册P53习题7.1T10命制.教材习
题和高考题都是利用条件概率公式P(B|A)=进行推理并证明指
定结论,高考题的难度略高于教材习题,考查了逻辑推理、数学运算等学科核心素养,难度中等.
第九章 计数原理、概率、随机变量及其分布
必修1 中国特色社会主义
试题评价:本题的医疗团队课题研究问题有着现实的背景,以医疗团队研究地方性疾病与居民卫生习惯的关系为情境素材,引导学生用所学知识解决社会实践中的问题,属于生活实践情境.
附:(人教A版选择性必修第二册P53习题7.1T10)证明:当P(AB)>0时,P(ABC)=P(A)P(B|A)·P(C|AB).据此你能发现计算P(A1A2…An)的公式吗?
第九章 计数原理、概率、随机变量及其分布
第1课时 两个计数原理
[考试要求] 1.理解分类加法计数原理和分步乘法计数原理.
2.会用两个计数原理分析和解决一些简单的实际问题.
考点一 分类加法计数原理
1.分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=______种不同的方法.
2.分类加法计数原理的推广:完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有N=____________________种不同的方法.
m+n
m1+m2+…+mn
[典例1] (1)(2024·天津南开区期末)甲、乙、丙三人踢毽子,互相传递,每人每次只能踢一下,若由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )
A.4种 B.5种 C.6种 D.12种
(2)椭圆=1(m>0,n>0)的焦点在x轴上,且m∈{1,2,3,4,5},n∈{1,2,3,4,5,6,7},则这样的椭圆的个数为( )
A.10 B.12 C.20 D.35
√
√
(1)C (2)A [(1)当开始甲将球传给乙时,经过4次传球后,球正好回到甲手中的传球方式有3种:
甲→乙→甲→丙→甲,甲→乙→甲→乙→甲,甲→乙→丙→乙→甲;
当开始甲将球传给丙时,经过4次传球后,球正好回到甲手中的传球方式有3种:
甲→丙→乙→丙→甲,甲→丙→甲→丙→甲,甲→丙→甲→乙→甲;
所以不同的传球方式有3+3=6(种).故选C.
(2)因为焦点在x轴上,所以m>n,以m的值为标准分类,由分类加法计数原理,可分为四类,第一类:当m=5时,n有4种选择;第二类:当m=4时,n有3种选择;第三类:当m=3时,n有2种选择;第四类:当m=2时,n有1种选择.故符合条件的椭圆共有10个.]
【教用·备选题】
母题探究 在本例(2)中,若m∈{1,2,…,k},n∈{1,2,…,k}(k∈N*),其他条件不变,这样的椭圆有多少个?
[解] 因为m>n,当m=k时,n=1,2,…,k-1;
当m=k-1时,n=1,2,…,k-2;
……
当m=3时,n=1,2;当m=2时,n=1.
所以共有1+2+…+(k-1)=(个)椭圆.
反思领悟 本例(1)要注意不能漏数,还要注意是否重复(多数);本例(2)要注意分类标准要统一,不能遗漏.
巩固迁移1 (人教A版选择性必修第三册P5例3改编)某影城有一些电影新上映,其中有2部科幻片、3部文艺片、2部喜剧片,小明从中任选1部电影观看,不同的选法种数为( )
A.2+3+2=7 B.1+1+1=3
C.2×3×2=12 D.(23)2=64
√
A [由分类加法计数原理可知,不同的选法种数为2+3+2=7.故选A.]
考点二 分步乘法计数原理
1.分步乘法计数原理:完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=______种不同的方法.
2.分步乘法计数原理的推广:完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事共有N=____________________种不同的方法.
m×n
m1×m2×…×mn
[典例2] (多选)(2024·合肥调研)现安排高二年级A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名同学只能选择一个工厂,且允许多人选择同一个工厂,则下列说法正确的是( )
A.共有43种不同的安排方法
B.若甲工厂必须有同学去,则不同的安排方法有37种
C.若A同学必须去甲工厂,则不同的安排方法有12种
D.若三名同学所选工厂各不相同,则不同的安排方法有24种
√
√
√
ABD [对于A,A,B,C三名同学到甲、乙、丙、丁四个工厂进行社会实践,每名学生有4种选法,则三名学生有4×4×4=43(种)选法,故A正确;
对于B,三人到四个工厂,有43=64(种)情况,其中甲工厂没有人去,即三人全部到乙、丙、丁三个工厂的情况有33=27(种),则甲工厂必须有同学去的安排方法有64—27=37(种),故B正确;
对于C,若同学A必须去甲工厂,剩下2名同学安排到4个工厂即可,有42=16(种)安排方法,故C错误;
对于D,若三名同学所选工厂各不相同,有4×3×2=24(种)安排方法,故D正确.]
反思领悟 利用分步乘法计数原理解题的策略
(1)明确题目中的“完成这件事”是什么,确定完成这件事需要几个步骤,且每步都是独立的.
(2)将这件事划分成几个步骤来完成,各步骤之间有一定的连续性,只有当所有步骤都完成了,整个事件才算完成.
巩固迁移2 (1)(2024·济南期末)大明湖是济南三大名胜之一,素有“泉城明珠”之美誉,自2017年1月1日起全面向社会免费开放.景区有东南西北4个大门,每个大门进去都有不同景致,小明从一个大门进,另一个大门出,则不同进出方式的种数为( )
A.7 B.8 C.12 D.16
(2)将4个不同的小球放入3个不同的盒子中,且每个盒子最多只能装3个球,则不同的放法有( )
A.60种 B.64种 C.78种 D.81种
√
√
(1)C (2)C [(1)根据题意,景区有4个大门,从一个大门进,有4种走法,
另一个大门出,有3种走法,则有4×3=12(种)不同的走法.故选C.
(2)不考虑每个盒子最多只能装3个球,有34种放法.
若将4个球放入同一个盒子中,有3种放法.
故不同的放法有34-3=78(种).故选C.]
考点三 两个计数原理的综合应用
两个计数原理的区别与联系
分类加法计数原理 分步乘法计数原理
相同点 用来计算完成一件事的方法种数
不同点 分类、相加 分步、相乘
每类方案中的每一种方法都能独立完成这件事 每步依次完成才算完成这件事情(每步中的每一种方法不能独立完成这件事)
注意点 类类独立,不重不漏 步步相依,缺一不可
提醒:分类加法计数原理与分步乘法计数原理是解决排列组合问题的基础,并贯穿其始终.
(1)分类加法计数原理中,完成一件事的方法属于其中一类,并且只属于其中一类.
(2)分步乘法计数原理中,各个步骤中的方法相互依存,步与步之间“相互独立,分步完成”.
考向1 与数字有关的问题
[典例3] (2024·洛阳期中)用0,1,2,3,4这五个数字组成没有重复数字的三位数,其中奇数共有( )
A.48个 B.24个
C.18个 D.12个
√
C [根据题意,三位数的个位数字必须为1或3,有2种情况,
百位数字不能为0,有3种情况,
十位数字在剩下的3个数字中任选1个,有3种情况,
则共有2×3×3=18(种)情况,即有18个符合题意的三位奇数.
故选C.]
反思领悟 本例中,要完成的“一件事”为组成无重复数字的三位奇数,所以百位数字不能为0,个位数字必须是奇数,因此应先分类、再分步.
巩固迁移3 从数字1,2,3,4中取出3个数字(允许重复)组成三位数,各位数字之和等于6,则这样的三位数的个数为( )
A.7 B.9
C.10 D.13
√
C [其中各位数字之和等于6的三位数可分为以下情形:
①由1,1,4三个数字组成的三位数:114,141,411,共3个;
②由1,2,3三个数字组成的三位数:123,132,213,231,312,321,共6个;
③由2,2,2三个数字可以组成1个三位数,即222.
共有3+6+1=10(个).]
考向2 与几何有关的问题
[典例4] 如果一条直线与一个平面垂直,那么称此直线与该平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A.48 B.18
C.24 D.36
√
D [分类讨论:第一类,对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有2×12=24(个);第二类,对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正交线面对”有2×6=12(个);第三类,对于每一条体对角线,没有符合题意的平面与之构成“正交线面对”.所以正方体中“正交线面对”共有24+12=36(个).故选D.]
反思领悟 解决本例的关键是画出正方体,弄清楚正方体中的垂直关系,合理分类将问题简化.
巩固迁移4 如果一条直线与一个平面平行,那么称此直线与平面构成一个“平行线面组”.在一个长方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是( )
A.60 B.48
C.36 D.24
√
B [长方体的6个表面构成的“平行线面组”的个数为6×6=36,另含4个顶点的6个面(非表面)构成的“平行线面组”的个数为6×2=12,故符合条件的“平行线面组”的个数是36+12=48.]
考向3 涂色、种植问题
[典例5] 中国是世界上最早发明雨伞的国家,伞是中国劳动人民一个重要的创造.如图所示的雨伞,其伞面被伞骨分成8个区域,每个区域分别印有数字1,2,3,…,8,现准备给该伞面的每个区域涂色,要求每个区域涂一种颜色,相邻两个区域所涂颜色不能相同,对称的两个区域(如区域1与区域5)所涂颜色相同.若有7种不同颜色的颜料可供选择,则不同的涂色方案有( )
A.1 050种 B.1 260种
C.1 302种 D.1 512种
√
C [由题意可得,只需确定区域1,2,3,4的颜色,即可确定整个伞面的涂色.
先涂区域1,有7种选择;再涂区域2,有6种选择.
当区域3与区域1涂的颜色不同时,区域3有5种选择,剩下的区域4有5种选择.
当区域3与区域1涂的颜色相同时,剩下的区域4有6种选择.
故不同的涂色方案有7×6×(5×5+1×6)=1 302(种).]
反思领悟 涂色问题,可按颜色的种数用分类加法计数原理分析,也可按不同的区域用分步乘法计数原理分析.
巩固迁移5 某学校有一块绿化用地,其形状如图所示.为了让效果更美观,要求在四个区域内种植花卉,且相邻区域花卉颜色不同.现有五种不同颜色的花卉可供选择,则不同的种植方案共有________种.(用数字作答)
180
180 [先在A中种植,有5种不同的种植方法,再在B中种植,有4种不同的种植方法,再在C中种植,有3种不同的种植方法,最后在D中种植,有3种不同的种植方法,
所以不同的种植方案共有5×4×3×3=180(种).]
随堂练习
√
1.(2025·广东汕头模拟)电脑调色板有红、绿、蓝三种基本颜色,每种颜色的色号均为0~255.在电脑上绘画可以分别从三种颜色的色号中各选一个配成一种颜色,那么在电脑上可配成的颜色种数为( )
A.2563 B.27
C.2553 D.6
A [分3步取色,第一、第二、第三次都有256种取法,根据分步乘法计数原理得,共可配成256×256×256=2563(种)颜色.]
2.(人教A版选择性必修第三册P5练习T1(1))一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这项工作,不同选法的种数是________.
9 [因为一项工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,所以从中选出1人来完成这项工作,不同选法的种数是5+4=9.]
9
3.(人教A版选择性必修第三册P5练习T1(2))从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同路线的条数是________.
6 [因为从A村去B村的道路有3条,从B村去C村的道路有2条,所以从A村经B村去C村,不同路线的条数是3×2=6.]
6
4.一个圆的圆周上均匀分布6个点,在这些点与圆心共7个点中,任取3个点,这3个点能构成不同的等边三角形的个数为________.
8
8 [如图1,由圆上相邻两个点和圆心可构成等边三角形,共有6个;
如图2,由圆上相间隔的三点可构成等边三角形,共有2个,
所以在这7个点中,任取3个点,这3个点能构成不同的等边三角形的个数为6+2=8. ]
【教用·备选题】
1.(2024·广州越秀区期末)学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,不同的选法种数为( )
A.10 B.15
C.60 D.125
√
D [由题意可分三步:甲同学有5种选法,乙同学有5种选法,丙同学有5种选法,
共5×5×5=125(种).故选D.]
2.(多选)(2024·宿迁期末)下列说法中正确的有( )
A.4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有43种报名方法
B.4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有34种报名方法
C.4名同学争夺跑步、跳高、跳远三项冠军(每项冠军只允许一人获得),共有43种可能结果
D.4名同学争夺跑步、跳高、跳远三项冠军(每项冠军只允许一人获得),共有34种可能结果
√
√
BC [对于A、B,4名同学选报跑步、跳高、跳远三个项目,每人报一项,每人都有3种选择,共有34种报名方法,所以A错误,B正确;
对于C、D,4名同学争夺跑步、跳高、跳远三项冠军(每项冠军只允许一人获得),每个冠军有4种可能,共有43种可能结果,所以C正确,D错误.故选BC.]
3.(2025·江西南昌模拟)四面体的顶点和各棱的中点共10个点.在这10个点中取4个不共面的点,则不同的取法种数为( )
A.141 B.144
C.150 D.155
√
A [从10个点中任取4个点有种取法,其中4点共面的情况有三类.
第一类,取出的4个点位于四面体的同一个面上,有种;
第二类,取任一条棱上的3个点及该棱所对棱的中点,这4点共面,有6种;
第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个顶点共面,有3种.
以上三类情况不合要求应减掉,
∴不同的取法共有-6-3=141(种).
故选A.]
4.(2024·北京朝阳区期末)用四种颜色给正四棱锥V-ABCD的五个顶点涂色,要求每个顶点涂一种颜色,且每条棱的两个顶点涂不同颜色,则不同的涂法有( )
A.72种 B.36种
C.12种 D.60种
√
A [①当用2种颜色涂A,B,C,D时,则A,C涂色相同,B,D涂色相同,共有=12(种)涂色方法,则涂V有2种涂色方法,
即给正四棱锥V-ABCD的五个顶点涂色,
共12×2=24(种)涂色方法;
②当用3种颜色涂A,B,C,D时,则A,
C涂色相同,B,D涂色不相同,或A,C涂色不相同,B,D涂色相同,共有=48(种)涂色方法,则涂V有1种涂色方法,
即给正四棱锥V-ABCD的五个顶点涂色,共48×1=48(种)涂色方法;
由①②得,不同的涂法有24+48=72(种).故选A.]
5.(2024·眉山仁寿县月考)已知0,1,2,3,4,5这六个数字.
(1)可以组成多少个无重复数字的三位数?
(2)可以组成多少个无重复数字的三位奇数?
(3)可以组成多少个无重复数字的小于1 000的自然数?
(4)可以组成多少个无重复数字的大于3 000且小于5 421的四位数?
[解] (1)分3步:
①先选百位数字有5种选法,
②十位数字有5种选法,
③个位数字有4种选法,
由分步乘法计数原理知所求三位数共有5×5×4=100(个).
(2)分3步:
①先选个位数字,由于组成的三位数是奇数,因此有3种选法,
②再选百位数字有4种选法,
③十位数字也有4种选法,
由分步乘法计数原理知所求三位数共有3×4×4=48(个).
(3)分3类:
①一位数,共有6个,
②两位数,先选十位数字,有5种选法,再选个位数字也有5种选法,共有5×5=25(个),
③三位数,先选百位数字,有5种选法,再选十位数字也有5种选法,再选个位数字,有4种选法,共有5×5×4=100(个),
因此,比1 000小的自然数共有6+25+100=131(个).
(4)分4类:
①千位数字为3或4时,后面三个数位上可随便选择,此时共有2×5×4×3=120(个),
②千位数字为5,百位数字为0,1,2,3之一时,共有4×4×3=48(个),
③千位数字为5,百位数字是4,十位数字为0,1之一时,共有2×3=6(个),
④5 420也满足条件.
故所求四位数共有120+48+6+1=175(个).
课后习题(五十九) 两个计数原理
1.(人教A版选择性必修第三册P11练习T2改编)在所有的两位数中,个位数字大于十位数字的两位数的个数是( )
A.18 B.36
C.72 D.48
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [法一:按十位上的数字分别是1,2,3,4,5,6,7,8分成八类,在每一类中满足条件的两位数分别有8个、7个、6个、5个、4个、3个、2个、1个.由分类加法计数原理知,满足条件的两位数的个数是8+7+6+5+4+3+2+1=36.
法二:按个位上的数字分别是2,3,4,5,6,7,8,9分成八类,在每一类中满足条件的两位数分别有1个、2个、3个、4个、5个、6个、7个、8个.由分类加法计数原理知,满足条件的两位数的个数是1+2+3+4+5+6+7+8=36.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版选择性必修第三册P27习题6.2T17改编)如图,用4种不同的颜色把图中A,B,C,D四块区域区分开,若相邻区域不能涂同一种颜色,则不同的涂法共有( )
A.144种 B.73种
C.48种 D.32种
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [第一步,给A区域涂色,有4种涂法;第二步,给B区域涂色,有3种涂法;第三步,给C区域涂色,有2种涂法;第四步,给D区域涂色,有2种涂法.所以共有4×3×2×2=48(种)涂法.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教A版选择性必修第三册P8例7改编)如图,将一条电路从A处到B处接通时,可以有________条不同的线路(每条线路仅含一条通路).
9
题号
1
3
5
2
4
6
8
7
9
10
11
12
9 [依题意,按上、中、下三种线路分为三类,上线路有2条,中线路有1条,下线路有2×3=6(条).根据分类加法计数原理知,共有2+1+6=9(条).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第三册P12习题6.1T8改编)5名学生报名参加四项体育比赛,每人限报一项,则不同的报名方法的种数为________.5名学生争夺四项比赛的冠军(冠军不并列),则获得冠军的可能性有________种.(用数字作答)
1 024 625 [5名学生参加四项体育比赛,每人限报一项,可逐个学生落实,每名学生有4种报名方法,共有45=1 024(种)不同的报名方法.5名学生争夺四项比赛的冠军,可对4个冠军逐一落实,每个冠军有5种获得的可能性,共有54=625(种)获得冠军的可能性.]
1 024
625
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·河池月考)一个4层书架上,分别放置科普类读物10本、人文类读物10本、自然类读物9本、漫画类读物8本,每本书各不相同,从中取出1本,则不同的取法共有( )
A.4种 B.7 200种
C.27种 D.37种
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [由题意知,每本书各不相同,从中取出1本,共有37本书,所以不同的取法共有37种.故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·临洮县期末)从由1,2,3,4,5组成的没有重复数字的两位数中任取一个,则这个两位数大于40的个数是( )
A.6 B.8
C.10 D.12
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [因为这个两位数大于40,
所以选取十位数为4或5,个位数不重复,则在剩余的4个数字里选择1个,
这个两位数大于40的个数为2×4=8.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·北京石景山区开学考试)首位数字是1,且恰有两个数字相同的四位数共有( )
A.216个 B.252个
C.324个 D.432个
√
D [①两个相同数字是1,一共有3×9×8种组合;
②两个相同数字不是1,同样一共有3×9×8种组合.
所以这样的四位数有2×3×9×8=432(个).故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·重庆万州区月考)设从东、西、南、北四面通往山顶的路分别有2,3,3,4条,现要从一面上山,从剩余三面中的任意一面下山,则下列结论正确的是( )
A.从东面上山有20种走法
B.从西面上山有27种走法
C.从南面上山有30种走法
D.从北面上山有32种走法
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [对于A,若从东面上山,上山的路有2条,下山的路有3+3+4=10(条),则有2×10=20(条),A正确;
对于B,若从西面上山,上山的路有3条,下山的路有2+3+4=9(条),则有3×9=27(条),B正确;
对于C,若从南面上山,上山的路有3条,下山的路有2+3+4=9(条),则有3×9=27(条),C错误;
对于D,若从北面上山,上山的路有4条,下山的路有2+3+3=8(条),则有4×8=32(条),D正确.
故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·临汾调考)如图所示的五个区域中,现有四种颜色可供选择,要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法有( )
A.24种 B.48种
C.72种 D.96种
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [分两种情况:
①A,C不同色,先涂A有4种,C有3种,E有2种,B,D有1种,有4×3×2×1=24(种);
②A,C同色,先涂A,C有4种,再涂E有3种,B,D各有2种,有4×3×2×2=48(种).
故不同的涂色方法有48+24=72(种).故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·杭州调研)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )
A.243 B.252
C.261 D.279
√
B [0,1,…,9共能组成9×10×10=900(个)三位数,
其中无重复数字的三位数有9×9×8=648(个),
故有重复数字的三位数有900-648=252(个).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·乐山期末)由数字2,3,4,5可组成______个三位数(各位上数字可重复,用数字作答).
64 [由题意,百位、十位和个位上的数字均有4种选法,
故由数字2,3,4,5可以组成4×4×4=64(个)三位数.]
64
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·连云港赣榆区月考)从0,1,2,3,4五个数字中选出3个数字组成一个三位数.
(1)可以组成多少个三位数?
(2)可以组成多少个无重复数字的三位数?
(3)可以组成多少个无重复数字的三位偶数?
[解] (1)三位数的首位不能为0,但可以有重复数字,首先考虑首位的排法,除0外共有4种方法,第二、三位可以排0,因此,根据分步乘法计数原理共有4×5×5=100(个).
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)三位数的首位不能为0,首先考虑首位的排法,除0外共有4种方法,第二位可以排0,
除首位排的数字外共有4种方法,第三位除前两位排的数字外共有3种方法,
因此,根据分步乘法计数原理共有4×4×3=48(个).
(3)偶数末位数字可取0,2,4,因此,可以分两类:
一类是末位数字是0,则有4×3=12(种)排法;
一类是末位数字不是0,则末位有2种排法,即2或4,再排首位,因0不能在首位,
所以有3种排法,十位有3种排法,因此有2×3×3=18(种)排法.
因此有12+18=30(种)排法.即可以排成30个无重复数字的三位偶数.
谢 谢 !
同课章节目录
