《高考快车道》2026版高三一轮总复习数学(基础版)102 第九章 第4课时 随机事件、频率与概率 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)102 第九章 第4课时 随机事件、频率与概率 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:02 | ||
图片预览











文档简介
(共79张PPT)
第九章 计数原理、概率、随机变量及其分布
第4课时 随机事件、频率与概率
[考试要求] 1.结合具体实例,理解样本点和有限样本空间的含义,理解随机事件与样本点的关系.
2.理解事件间的关系与运算,会计算一些随机事件所包含的样本点及事件发生的概率.
3.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率和概率的区别与联系.
4.理解古典概型及其概率计算公式.当直接求某一事件的概率较为复杂时,会转化为求几个互斥事件的概率之和或其对立事件的概率.
考点一 随机事件与样本空间
1.样本空间与样本点
(1)样本点:把随机试验E的每个可能的________称为样本点,常用ω表示.
(2)样本空间:__________的集合称为试验E的样本空间,常用Ω表示样本空间.如果一个随机试验有n个可能结果ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
基本结果
全体样本点
2.随机事件、必然事件与不可能事件
(1)随机事件:________________称为随机事件,简称事件,随机事件一般用大写字母A,B,C,…表示.在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
(2)随机事件的特殊情形:必然事件Ω(含有全部样本点)、不可能事件 (不含任何样本点)、基本事件(只包含一个样本点).
样本空间Ω的子集
[典例1] (1)(2025·湖北襄阳模拟)已知集合A是集合B的真子集,则下列关于非空集合A,B的四个命题:
①若任取x∈A,则x∈B是必然事件;
②若任取x A,则x∈B是不可能事件;
③若任取x∈B,则x∈A是随机事件;
④若任取x B,则x A是必然事件.
其中正确的命题有( )
A.1个 B.2个
C.3个 D.4个
√
(2)袋中有大小、形状相同的红球、黑球各一个,现在有放回地随机摸3次,每次摸取一个,观察摸出球的颜色,则此随机试验的样本点个数为( )
A.5 B.6
C.7 D.8
√
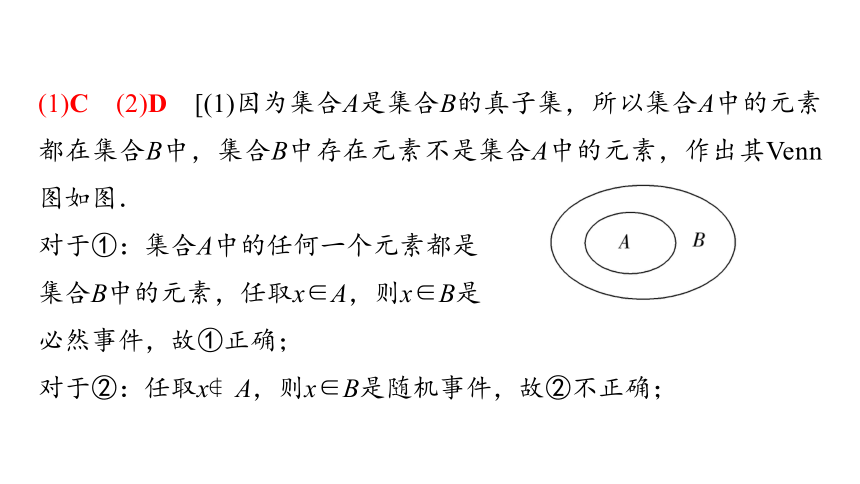
(1)C (2)D [(1)因为集合A是集合B的真子集,所以集合A中的元素都在集合B中,集合B中存在元素不是集合A中的元素,作出其Venn图如图.
对于①:集合A中的任何一个元素都是
集合B中的元素,任取x∈A,则x∈B是
必然事件,故①正确;
对于②:任取x A,则x∈B是随机事件,故②不正确;
对于③:因为集合A是集合B的真子集,集合B中存在元素不是集合A中的元素,集合B中也存在集合A中的元素,所以任取x∈B,则x∈A是随机事件,故③正确;
对于④:因为集合A中的任何一个元素都是集合B中的元素,任取x B,则x A是必然事件,故④正确.所以①③④正确,正确的命题有3个.故选C.
(2)因为是有放回地随机摸3次,所以随机试验的样本空间为Ω={(红,红,红),(红,红,黑),(红,黑,红),(红,黑,黑),(黑,红,红),(黑,红,黑),(黑,黑,红),(黑,黑,黑)},共8个样本点.]
反思领悟 本例(1)判断一个事件主要看结果是否发生;本例(2)确定样本空间,首先必须明确事件发生的条件,然后按一定次序列出问题的答案.
巩固迁移1 (1)下列事件:①任取一个整数,被2整除;②小明同学在某次数学测试中成绩(满分150分)一定不低于120分;③甲、乙两人进行竞技比赛,甲的实力远胜于乙,在一次比赛中甲一定获胜;④当圆的半径变为原来的2倍时,圆的面积是原来的4倍.其中随机事件的个数是( )
A.4 B.3
C.2 D.1
√
(2)(人教A版必修第二册P231练习T3改编)从1,2,3,…,10中任意选一个数,这个试验的样本空间为_____________________________
_________,“它是偶数”这一事件包含的样本点个数为________.
(1)B (2)Ω={1,2,3,4,5,6,7,8,9,10} 5 [(1)①②③均是可能发生也可能不发生的事件,为随机事件,④是一定发生的事件,为必然事件.故选B.
Ω={1,2,3,4,5,6,7,8,
9,10}
5
(2)任选一个数,共有10种不同选法,故样本空间为Ω={1,2,3,4,5,6,7,8,9,10},其中偶数共有5种,故“它是偶数”这一事件包含的样本点个数为5.]
考点二 事件的关系与运算
事件的关 系或运算 含义 符号表示 图形表示
包含 A发生导致B发生 ______
并事件 (和事件) A与B至少一个发生 ______________
A B
A∪B或A+B
事件的关 系或运算 含义 符号表示 图形表示
交事件 (积事件) A与B同时发生 ____________
互斥(互 不相容) A与B不能同时发生 __________
互为对立 A与B有且仅有一个发生 __________,__________
A∩B或AB
A∩B=
A∪B=Ω
A∩B=
[典例2] (1)从装有十个红球和十个白球的罐子里任取两球,下列情况中是互斥而不对立的两个事件的是( )
A.至少有一个红球;至少有一个白球
B.恰有一个红球;都是白球
C.至少有一个红球;都是白球
D.至多有一个红球;都是红球
√
(2)(多选)对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设事件A={两弹都击中飞机},事件B={两弹都没击中飞机},事件C={恰有一弹击中飞机},事件D={至少有一弹击中飞机},则下列关系正确的是( )
A.A∩D= B.B∩D=
C.A∪C=D D.A∪B=B∪D
√
√
(1)B (2)BC [(1)对于A,“至少有一个红球”可能为一个红球、一个白球,“至少有一个白球”可能为一个白球、一个红球,故两个事件可能同时发生,所以不是互斥事件;对于B,“恰有一个红球”,则另一个必是白球,与“都是白球”是互斥事件,而任取两球还可能都是红球,故两事件不是对立事件;对于C,“至少有一个红球”为都是红球或一红一白,与“都是白球”显然是对立事件;对于D,“至多有一个红球”为都是白球或一红一白,与都是红球是对立事件.故选B.
(2)“恰有一弹击中飞机”指第一枚击中、第二枚没中或第一枚没中、第二枚击中,
“至少有一弹击中飞机”包含两种情况,一种是恰有一弹击中,另一种是两弹都击中,故A∩D≠ ,B∩D= ,A∪C=D,A∪B≠B∪D.故选BC.]
反思领悟 互斥事件、对立事件一般用定义判断,不可能同时发生的两个事件为互斥事件(即A∩B是一个不可能事件);两个事件,若有且仅有一个发生(即A∩B= 且A∪B=Ω),则这两个事件为对立事件;对立事件一定是互斥事件,而互斥事件未必是对立事件.
巩固迁移2 (多选)从装有2个红球和2个黑球的口袋中任取2个小球,则下列结论正确的是( )
A.“至少一个红球”和“都是红球”是互斥事件
B.“恰有一个黑球”和“都是黑球”是互斥事件
C.“至少一个黑球”和“都是红球”是对立事件
D.“恰有一个红球”和“都是红球”是对立事件
√
√
BC [不妨记两个黑球为A1,A2,两个红球为B1,B2,从中取出2个球,则所有样本点如下:A1A2,A1B1,A1B2,A2B1,A2B2,B1B2,恰有一个黑球包括:A1B1,A1B2,A2B1,A2B2,都是黑球包括A1A2,两个事件没有共同的样本点,故互斥,B正确;
至少一个黑球包括:A1A2,A1B1,A1B2,A2B1,A2B2,都是红球包括B1B2,
两个事件没有共同的样本点,且两者包括的样本点所组成的集合的并集为全部样本点所组成的集合,故对立,C正确.
同理可知A、D都不正确,故选BC.]
考点三 频率与概率
1.事件的概率:对随机事件发生__________的度量(数值)称为事件的概率,事件A的概率用P(A)表示.
2.频率的稳定性:一般地,随着试验次数n的增大,频率偏离概率的幅度会____,即事件A发生的频率fn(A)会逐渐______事件A发生的概率P(A).我们称频率的这个性质为频率的稳定性.可以用频率fn(A)估计概率P(A).
可能性大小
缩小
稳定于
[典例3] 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到达火车站的人进行调查,调查结果如下:
所用时间(分钟) 10~20 20~30 30~40 40~50 50~60
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(1)试估计40分钟内不能赶到火车站的概率;
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
[解] (1)由已知共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44(人),
∴用频率估计相应的概率为P==0.44.
(2)选择L1的有60人,选择L2的有40人,故由调查结果得频率为
所用时间(分钟) 10~20 20~30 30~40 40~50 50~60
L1的频率 0.1 0.2 0.3 0.2 0.2
L2的频率 0 0.1 0.4 0.4 0.1
(3)设A1,A2分别表示甲选择L1和L2时,在40分钟内赶到火车站;B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站.
由(2)知P(A1)=0.1+0.2+0.3=0.6,
P(A2)=0.1+0.4=0.5,
∵P(A1)>P(A2),∴甲应选择L1.
同理,P(B1)=0.1+0.2+0.3+0.2=0.8,
P(B2)=0.1+0.4+0.4=0.9,
∵P(B1)反思领悟 (1)解题的关键是根据统计图表给出的满足条件的事件发生的频数,计算频率,用频率估计概率.
(2)频率反映了一个随机事件出现的频繁程度,频率是随机的,而概率是一个确定的值,通常用概率来反映随机事件发生的可能性的大小,即通过大量的重复试验,事件发生的频率会逐步趋近于某一个常数,这个常数就是概率.因此用频率来作为随机事件概率的估计值.
巩固迁移3 我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为________.
0.98 [经停该站高铁列车所有车次的平均正点率的估计值为=0.98.]
0.98
考点四 互斥与对立事件的概率计算
1.概率的基本性质
性质1:对任意的事件A,都有P(A)__0.
性质2:必然事件的概率为1,不可能事件的概率为0,即P(Ω)=__,P( )=__.
性质3:如果事件A与事件B互斥,那么P(A∪B)=______________.
≥
1
0
P(A)+P(B)
性质4:如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=____________.
性质5:如果A B,那么P(A)≤P(B),由该性质可得,对于任意事件A,因为 A Ω,所以0≤P(A)≤1.
性质6:设A,B是一个随机试验中的两个事件,我们有P(A∪B)=P(A)+P(B)-P(A∩B).
1-P(B)
2.从集合的角度理解互斥事件和对立事件
(1)几个事件彼此互斥,是指由各个事件所含的结果组成的集合的交集为空集.
(2)事件A的对立事件所含的结果组成的集合,是全集中由事件A所含的结果组成的集合的补集.
3.概率加法公式的推广
当一个事件包含多个结果且各个结果彼此互斥时,要用到概率加法公式的推广,即
P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
[典例4] 经统计,在某储蓄所一个营业窗口等候的人数相应的概率如下:
排队人数 0 1 2 3 4 5人及5人以上
概率 0.1 0.16 0.3 0.3 0.1 0.04
求:(1)至多2人排队等候的概率;
(2)至少3人排队等候的概率.
[解] 记“无人排队等候”为事件A,“1人排队等候”为事件B,“2人排队等候”为事件C,“3人排队等候”为事件D,“4人排队等候”为事件E,“5人及5人以上排队等候”为事件F,则事件A,B,C,D,E,F彼此互斥.
(1)记“至多2人排队等候”为事件G,则G=A+B+C,所以P(G)=P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)法一:记“至少3人排队等候”为事件H,则H=D+E+F,
所以P(H)=P(D+E+F)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44.
法二:记“至少3人排队等候”为事件H,则其对立事件为事件G,所以P(H)=1-P(G)=0.44.
反思领悟 求复杂的互斥事件的概率的两种方法
(1)直接求解法,将所求事件的概率分解为一些彼此互斥的事件的概率的和,运用互斥事件的概率求和公式计算.
(2)间接求解法,先求此事件的对立事件的概率,再用公式P(A)=1-P(),即运用逆向思维(正难则反).特别是“至多”“至少”型题目,用间接求解法就显得较简便.
巩固迁移4 某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C.求:
(1)P(A),P(B),P(C);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
[解] (1)P(A)=,P(B)==,P(C)==.
(2)因为事件A,B,C两两互斥,所以P(A∪B∪C)=P(A)+P(B)+
P(C)==.故1张奖券的中奖概率为.
(3)设“1张奖券不中特等奖且不中一等奖”为事件N,由对立事件概
率公式得P(N)=1-P(A+B)=1-=.故1张奖券不中特等奖且不中一等奖的概率为.
随堂练习
√
1.(人教A版必修第二册P235练习T2改编)掷一枚质地均匀的骰子,“向上的点数是1或3”为事件A,“向上的点数是1或5”为事件B,则( )
A.A∪B表示向上的点数是1或3或5
B.A=B
C.A∪B表示向上的点数是1或3
D.A∩B表示向上的点数是1或5
A [设A={1,3},B={1,5},则A∩B={1},A∪B={1,3,5},∴A≠B,A∩B表示向上的点数是1,A∪B表示向上的点数是1或3或5.]
2.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4 500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如表:
满意情况 不满意 比较满意 满意 非常满意
人数 200 n 2 100 1 000
√
根据表中数据,估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是( )
A. B. C. D.
C [由题意知n=4 500-200-2 100-1 000=1 200,所以在网上购物的消费者群体中对网上购物“比较满意”或“满意”的总人数为1
200+2 100=3 300,所以在网上购物的消费者群体中对网上购物“比较满意”或“满意”的频率为=.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是.]
3.(2024·福州台江区期末)从装有3个黄球和4个蓝球的口袋内任取3个球,那么互斥不对立的事件是( )
A.恰有一个黄球与恰有一个蓝球
B.至少有一个黄球与都是黄球
C.至少有一个黄球与都是蓝球
D.至少有一个黄球与至少有一个蓝球
√
A [从装有3个黄球和4个蓝球的口袋内任取3个球,不同的取球情况共有以下4种:
①3个球全是黄球;②2个黄球和1个蓝球;③1个黄球和2个蓝球;④3个球全是蓝球.
对于A,恰有一个黄球是情况③,恰有一个蓝球是情况②,
∴恰有一个黄球与恰有一个蓝球是互斥不对立的事件,故A正确;
对于B,至少有一个黄球是情况①②③,都是黄球是情况①,
∴至少有一个黄球与都是黄球能同时发生,不是互斥事件,故B错误;
对于C,至少有一个黄球是情况①②③,都是蓝球是情况④,
∴至少有一个黄球与都是蓝球是对立事件,故C错误;
对于D,至少有一个黄球是情况①②③,至少有一个蓝球是情况②③④,
∴至少有一个黄球与至少有一个蓝球能同时发生,不是互斥事件,故D错误.
故选A.]
4.(2024·绍兴越城区期末)从含有6件次品的50件产品中任取4件,观察其中次品数,这个试验的样本空间Ω=_______________.
{0,1,2,3,4} [取出的4件产品中,最多有4件次品,最少是没有次品.
所以样本空间Ω={0,1,2,3,4}.]
{0,1,2,3,4}
【教用·备选题】
1.(2024·达州期末)将两枚质地均匀的骰子同时投掷,设事件A=“两枚骰子掷出点数均为偶数”,若连续投掷100次,则事件A发生的频数为( )
A.20 B.25
C.50 D.无法确定
√
D [任意一次随机试验中,随机事件的发生具有随机性,即频率(频数与试验次数的比值)具有随机性,而随试验次数的增加,事件发生的频率逐渐稳定于概率,具有稳定性,
则投掷100次的试验中,事件A发生的频率有随机性,故无法确定.故选D.]
2.(2024·安庆大观区期末)设A,B是一个随机试验中的两个事件且P(A)=,P()=,P(B+A)=,则P(B)=( )
A. B.
C. D.
√
A [因为P(A)=,P()=,P(B)=,
因为B·A)=0,
所以P()=P(B)-P(AB)+P(A)-P(AB)
=-2P(AB)=,故P(AB)=,故P(B)=P(B)-P(AB)==.
故选A.]
3.(2024·乌鲁木齐期末)在一个不透明的纸盒中装有6个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.8附近,则袋子中红球约有________个.
24 [设袋子中红球约有x个,利用频率的稳定值来估算概率,
则=0.8,
解得x=24,即袋子中红球约有24个.]
24
4.(2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
乙分厂产品等级的频数分布表
等级 A B C D
频数 28 17 34 21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
[解] (1)由试加工产品等级的频数分布表知,
甲分厂加工出来的一件产品为A级品的概率的估计值为=0.4;
乙分厂加工出来的一件产品为A级品的概率的估计值为=0.28.
(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为
利润 65 25 -5 -75
频数 40 20 20 20
因此甲分厂加工出来的100件产品的平均利润为
=15.
由数据知乙分厂加工出来的100件产品利润的频数分布表为
利润 70 30 0 -70
频数 28 17 34 21
因此乙分厂加工出来的100件产品的平均利润为
=10.
比较甲、乙两分厂加工的产品的平均利润,厂家应选甲分厂承接加工业务.
课后习题(六十二) 随机事件、频率与概率
1.(多选)(人教A版必修第二册P235练习T2改编)将一枚质地均匀的骰子向上抛掷一次,设事件A=“向上的一面出现奇数点”,事件B=“向上的一面出现的点数不超过2”,事件C=“向上的一面出现的点数不小于4”,则下列说法中正确的有( )
A.B=
B.C= “向上的一面出现的点数大于3”
C.AC= “向上的一面出现的点数不小于3”
D.AC= “向上的一面出现的点数为2”
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
BC [由题意知事件A包含的样本点:向上的一面出现的点数为1,3,5;事件B包含的样本点:向上的一面出现的点数为1,2;事件C包含的样本点:向上的一面出现的点数为4,5,6,所以B=“向上的一面出现的点数为2”,故A错误;C=“向上的一面出现的点数为4或5或6”,故B正确;AC=“向上的一面出现的点数为3或4或5或6”,故C正确;AC=“向上的一面出现的点数为5”,故D错误.故选BC.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版必修第二册P257练习T1,T2改编)下列说法正确的是( )
A.甲、乙两人做游戏:甲、乙两人各写一个数字,若都是奇数或都是偶数,则甲胜,否则乙胜,这个游戏公平
B.做n次随机试验,事件A发生的频率就是事件A发生的概率
C.某地发行福利彩票,回报率为47%,某人花了100元买该福利彩票,一定会有47元的回报
D.有甲、乙两种报纸可供某人订阅,事件B=“某人订阅甲报纸”是必然事件
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [对于A,甲、乙两人各写一个数字,所有可能的结果为(奇,偶),
(奇,奇),(偶,奇),(偶,偶),则都是奇数或都是偶数的概率为,故游
戏是公平的;
对于B,随着试验次数的增加,频率偏离概率很大的可能性会越来越小,故事件A发生的频率就是事件A发生的概率是不正确的;
对于C,某人花100元买福利彩票,中奖或者不中奖都有可能,但事先无法预料,故C不正确;
对于D,事件B可能发生也可能不发生,故事件B是随机事件,故D不正确.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(苏教版必修第二册P292练习T1改编)某人射击一次,设事件A=“击中环数小于8”,事件B=“击中环数大于8”,事件C=“击中环数不小于8”,事件D=“击中环数不大于9”,则下列说法正确的是( )
A.A和B为对立事件
B.B和C为互斥事件
C.A和C为对立事件
D.B和D为互斥事件
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [由题意,事件A=“击中环数小于8”与事件B=“击中环数大于8”是互斥事件但不是对立事件,故A选项错误;事件B=“击中环数大于8”与事件C=“击中环数不小于8”,能同时发生,所以不是互斥事件,故B选项错误;事件A=“击中环数小于8”与事件C=“击中环数不小于8”是对立事件,故C选项正确;事件B=“击中环数大于8”与事件D=“击中环数不大于9”能同时发生,不是互斥事件,故D选项错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版必修第二册P256例1改编)一个四面体的四个面上分别标记1,2,3,4,重复抛掷这个四面体100次,记录每个面落在桌面的次数(如表).如果再抛掷一次,估计标记3的面落在桌面上的概率为________.
落在桌面上的面 1 2 3 4
频数 19 23 22 36
0.22
题号
1
3
5
2
4
6
8
7
9
10
11
12
0.22 [由题表知,标记3的面落在桌面上的频率为=0.22,故其概率的估计值为0.22.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·上海普陀区模拟)从放有两个红球、一个白球的袋子中一次任意取出两个球,两个红球分别标记为A,B,白球标记为C,则它的一个样本空间可以是( )
A.{AB,BC}
B.{AB,AC,BC}
C.{AB,BA,BC,CB}
D.{AB,BA,AC,CA,CB}
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [两个红球分别标记为A,B,白球标记为C,
则一次任意取出两个球的情况为AB,AC,BC,即它的一个样本空间可以是{AB,AC,BC}.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·西宁期末)有一个人在打靶中,连续射击2次,事件“至少有1次中靶”的对立事件是( )
A.至多有1次中靶 B.2次都中靶
C.2次都不中靶 D.只有1次中靶
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [由于两个事件互为对立事件时,这两件事不能同时发生,且这两件事的和事件是一个必然事件,
再由于一个人在打靶中,连续射击2次,事件“至少有1次中靶”的反面为“2次都不中靶”,故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·长治期末)下列说法正确的是( )
A.甲、乙两人进行羽毛球比赛,甲胜的概率为,则比赛4场,甲一定胜3场
B.概率是随机的,在试验前不能确定
C.事件A,B满足A B,则P(A)<P(B)
D.天气预报中,预报明天降水概率为90%,是指降水的可能性是90%
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [对于A,甲、乙两人比赛,甲胜的概率为,是指每场比赛,甲胜的可能性为,
则比赛4场,甲可能胜4场、3场、2场、1场、0场,故A错误;
对于B,随机试验的频率是变化的,概率是频率的稳定值,是固定的,故B错误;
对于C,事件A,B满足A B,则P(A)≤P(B),故C错误;
对于D,天气预报中,预报明天降水概率为90%,是指降水的可能性是90%,故D正确.
故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2024·烟台期末)若事件A与B互为对立事件,且P(A)=0.4,则P(B)=( )
A.0 B.0.4
C.0.6 D.1
√
C [由对立事件的概率公式,得P(B)=1-P(A)=0.6.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·重庆期末)已知两个互斥事件A,B满足P(A+B)=0.5,P(A)=0.2,则P(B)=( )
A.0.4 B.0.3
C.0.6 D.0.1
√
B [因为A,B为互斥事件,
P(A+B)=0.5,P(A)=0.2,
所以P(B)=0.5-0.2=0.3.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(多选)(2024·溧阳市期末)某篮球运动员进行投篮训练,连续投篮两次,设事件A表示随机事件“两次都投中”,事件B表示随机事件“两次都未投中”,事件C表示随机事件“恰有一次投中”,事件D表示随机事件“至少有一次投中”,则下列关系正确的是( )
A.A D B.B∩D=
C.A∪B=B∪D D.A∪C=D
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [事件A表示“两次都投中”;事件B表示“两次都未投中”;事件C表示“恰有一次投中”;事件D表示“至少有一次投中”,即表示“两次都投中”或“恰有一次投中”.
A:事件A表示“两次都投中”,事件D表示“至少有一次投中”,故A D,故A正确;
B:事件B和事件D是对立事件,故B∩D= ,故B正确;
C:事件A∪B表示“两次都投中”或“两次都未投中”,
而事件B∪D表示“两次都未投中”“两次都投中”或“恰有一次投中”,故C错误;
D:事件A∪C表示“两次都投中”或“恰有一次投中”,故A∪C=D,故D正确.
故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·太原期末)投掷两枚质地均匀的硬币,用ai表示“第i枚硬币正面朝上”,bi表示“第i枚硬币反面朝上”(i=1,2),则该试验的样本空间Ω=____________________________________.
{(a1,a2),(a1,b2),(b1,a2),(b1,b2)} [由题意可知,该试验的样本空间Ω={(a1,a2),(a1,b2),(b1,a2),(b1,b2)}.]
{(a1,a2),(a1,b2),(b1,a2),(b1,b2)}
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·荆州调考)某河流上的一座水力发电站,每年六月的发电量Y(单位:万千瓦时)与该河上游在六月份的降雨量X(单位:毫米)有关.据统计,当X=70时,Y=460;X每增加10,Y增加5.已知近20年X的值为140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的频率分布表:
近20年六月份降雨量频率分布表
降雨量 70 110 140 160 200 220
频率
(2)假定每年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求明年六月份该水力发电站的发电量低于490万千瓦时或超过530万千瓦时的概率.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)在所给数据中,降雨量为110毫米的有3个,降雨量为160毫米的有7个,降雨量为200毫米的有3个.
故近20年六月份降雨量频率分布表为
降雨量 70 110 140 160 200 220
频率
(2)根据题意,Y=460+×5=+425,故P(“发电量低于490万千瓦时或超过530万千瓦时”)=P(Y<490或Y>530)=P(X<130或X>210)=P(X=70)+P(X=110)+P(X=220)==.
故明年六月份该水力发电站的发电量低于490万千瓦时或超过530万千瓦时的概率为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
第九章 计数原理、概率、随机变量及其分布
第4课时 随机事件、频率与概率
[考试要求] 1.结合具体实例,理解样本点和有限样本空间的含义,理解随机事件与样本点的关系.
2.理解事件间的关系与运算,会计算一些随机事件所包含的样本点及事件发生的概率.
3.了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率和概率的区别与联系.
4.理解古典概型及其概率计算公式.当直接求某一事件的概率较为复杂时,会转化为求几个互斥事件的概率之和或其对立事件的概率.
考点一 随机事件与样本空间
1.样本空间与样本点
(1)样本点:把随机试验E的每个可能的________称为样本点,常用ω表示.
(2)样本空间:__________的集合称为试验E的样本空间,常用Ω表示样本空间.如果一个随机试验有n个可能结果ω1,ω2,…,ωn,则称样本空间Ω={ω1,ω2,…,ωn}为有限样本空间.
基本结果
全体样本点
2.随机事件、必然事件与不可能事件
(1)随机事件:________________称为随机事件,简称事件,随机事件一般用大写字母A,B,C,…表示.在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生.
(2)随机事件的特殊情形:必然事件Ω(含有全部样本点)、不可能事件 (不含任何样本点)、基本事件(只包含一个样本点).
样本空间Ω的子集
[典例1] (1)(2025·湖北襄阳模拟)已知集合A是集合B的真子集,则下列关于非空集合A,B的四个命题:
①若任取x∈A,则x∈B是必然事件;
②若任取x A,则x∈B是不可能事件;
③若任取x∈B,则x∈A是随机事件;
④若任取x B,则x A是必然事件.
其中正确的命题有( )
A.1个 B.2个
C.3个 D.4个
√
(2)袋中有大小、形状相同的红球、黑球各一个,现在有放回地随机摸3次,每次摸取一个,观察摸出球的颜色,则此随机试验的样本点个数为( )
A.5 B.6
C.7 D.8
√
(1)C (2)D [(1)因为集合A是集合B的真子集,所以集合A中的元素都在集合B中,集合B中存在元素不是集合A中的元素,作出其Venn图如图.
对于①:集合A中的任何一个元素都是
集合B中的元素,任取x∈A,则x∈B是
必然事件,故①正确;
对于②:任取x A,则x∈B是随机事件,故②不正确;
对于③:因为集合A是集合B的真子集,集合B中存在元素不是集合A中的元素,集合B中也存在集合A中的元素,所以任取x∈B,则x∈A是随机事件,故③正确;
对于④:因为集合A中的任何一个元素都是集合B中的元素,任取x B,则x A是必然事件,故④正确.所以①③④正确,正确的命题有3个.故选C.
(2)因为是有放回地随机摸3次,所以随机试验的样本空间为Ω={(红,红,红),(红,红,黑),(红,黑,红),(红,黑,黑),(黑,红,红),(黑,红,黑),(黑,黑,红),(黑,黑,黑)},共8个样本点.]
反思领悟 本例(1)判断一个事件主要看结果是否发生;本例(2)确定样本空间,首先必须明确事件发生的条件,然后按一定次序列出问题的答案.
巩固迁移1 (1)下列事件:①任取一个整数,被2整除;②小明同学在某次数学测试中成绩(满分150分)一定不低于120分;③甲、乙两人进行竞技比赛,甲的实力远胜于乙,在一次比赛中甲一定获胜;④当圆的半径变为原来的2倍时,圆的面积是原来的4倍.其中随机事件的个数是( )
A.4 B.3
C.2 D.1
√
(2)(人教A版必修第二册P231练习T3改编)从1,2,3,…,10中任意选一个数,这个试验的样本空间为_____________________________
_________,“它是偶数”这一事件包含的样本点个数为________.
(1)B (2)Ω={1,2,3,4,5,6,7,8,9,10} 5 [(1)①②③均是可能发生也可能不发生的事件,为随机事件,④是一定发生的事件,为必然事件.故选B.
Ω={1,2,3,4,5,6,7,8,
9,10}
5
(2)任选一个数,共有10种不同选法,故样本空间为Ω={1,2,3,4,5,6,7,8,9,10},其中偶数共有5种,故“它是偶数”这一事件包含的样本点个数为5.]
考点二 事件的关系与运算
事件的关 系或运算 含义 符号表示 图形表示
包含 A发生导致B发生 ______
并事件 (和事件) A与B至少一个发生 ______________
A B
A∪B或A+B
事件的关 系或运算 含义 符号表示 图形表示
交事件 (积事件) A与B同时发生 ____________
互斥(互 不相容) A与B不能同时发生 __________
互为对立 A与B有且仅有一个发生 __________,__________
A∩B或AB
A∩B=
A∪B=Ω
A∩B=
[典例2] (1)从装有十个红球和十个白球的罐子里任取两球,下列情况中是互斥而不对立的两个事件的是( )
A.至少有一个红球;至少有一个白球
B.恰有一个红球;都是白球
C.至少有一个红球;都是白球
D.至多有一个红球;都是红球
√
(2)(多选)对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设事件A={两弹都击中飞机},事件B={两弹都没击中飞机},事件C={恰有一弹击中飞机},事件D={至少有一弹击中飞机},则下列关系正确的是( )
A.A∩D= B.B∩D=
C.A∪C=D D.A∪B=B∪D
√
√
(1)B (2)BC [(1)对于A,“至少有一个红球”可能为一个红球、一个白球,“至少有一个白球”可能为一个白球、一个红球,故两个事件可能同时发生,所以不是互斥事件;对于B,“恰有一个红球”,则另一个必是白球,与“都是白球”是互斥事件,而任取两球还可能都是红球,故两事件不是对立事件;对于C,“至少有一个红球”为都是红球或一红一白,与“都是白球”显然是对立事件;对于D,“至多有一个红球”为都是白球或一红一白,与都是红球是对立事件.故选B.
(2)“恰有一弹击中飞机”指第一枚击中、第二枚没中或第一枚没中、第二枚击中,
“至少有一弹击中飞机”包含两种情况,一种是恰有一弹击中,另一种是两弹都击中,故A∩D≠ ,B∩D= ,A∪C=D,A∪B≠B∪D.故选BC.]
反思领悟 互斥事件、对立事件一般用定义判断,不可能同时发生的两个事件为互斥事件(即A∩B是一个不可能事件);两个事件,若有且仅有一个发生(即A∩B= 且A∪B=Ω),则这两个事件为对立事件;对立事件一定是互斥事件,而互斥事件未必是对立事件.
巩固迁移2 (多选)从装有2个红球和2个黑球的口袋中任取2个小球,则下列结论正确的是( )
A.“至少一个红球”和“都是红球”是互斥事件
B.“恰有一个黑球”和“都是黑球”是互斥事件
C.“至少一个黑球”和“都是红球”是对立事件
D.“恰有一个红球”和“都是红球”是对立事件
√
√
BC [不妨记两个黑球为A1,A2,两个红球为B1,B2,从中取出2个球,则所有样本点如下:A1A2,A1B1,A1B2,A2B1,A2B2,B1B2,恰有一个黑球包括:A1B1,A1B2,A2B1,A2B2,都是黑球包括A1A2,两个事件没有共同的样本点,故互斥,B正确;
至少一个黑球包括:A1A2,A1B1,A1B2,A2B1,A2B2,都是红球包括B1B2,
两个事件没有共同的样本点,且两者包括的样本点所组成的集合的并集为全部样本点所组成的集合,故对立,C正确.
同理可知A、D都不正确,故选BC.]
考点三 频率与概率
1.事件的概率:对随机事件发生__________的度量(数值)称为事件的概率,事件A的概率用P(A)表示.
2.频率的稳定性:一般地,随着试验次数n的增大,频率偏离概率的幅度会____,即事件A发生的频率fn(A)会逐渐______事件A发生的概率P(A).我们称频率的这个性质为频率的稳定性.可以用频率fn(A)估计概率P(A).
可能性大小
缩小
稳定于
[典例3] 如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到达火车站的人进行调查,调查结果如下:
所用时间(分钟) 10~20 20~30 30~40 40~50 50~60
选择L1的人数 6 12 18 12 12
选择L2的人数 0 4 16 16 4
(1)试估计40分钟内不能赶到火车站的概率;
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.
[解] (1)由已知共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44(人),
∴用频率估计相应的概率为P==0.44.
(2)选择L1的有60人,选择L2的有40人,故由调查结果得频率为
所用时间(分钟) 10~20 20~30 30~40 40~50 50~60
L1的频率 0.1 0.2 0.3 0.2 0.2
L2的频率 0 0.1 0.4 0.4 0.1
(3)设A1,A2分别表示甲选择L1和L2时,在40分钟内赶到火车站;B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站.
由(2)知P(A1)=0.1+0.2+0.3=0.6,
P(A2)=0.1+0.4=0.5,
∵P(A1)>P(A2),∴甲应选择L1.
同理,P(B1)=0.1+0.2+0.3+0.2=0.8,
P(B2)=0.1+0.4+0.4=0.9,
∵P(B1)
(2)频率反映了一个随机事件出现的频繁程度,频率是随机的,而概率是一个确定的值,通常用概率来反映随机事件发生的可能性的大小,即通过大量的重复试验,事件发生的频率会逐步趋近于某一个常数,这个常数就是概率.因此用频率来作为随机事件概率的估计值.
巩固迁移3 我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为________.
0.98 [经停该站高铁列车所有车次的平均正点率的估计值为=0.98.]
0.98
考点四 互斥与对立事件的概率计算
1.概率的基本性质
性质1:对任意的事件A,都有P(A)__0.
性质2:必然事件的概率为1,不可能事件的概率为0,即P(Ω)=__,P( )=__.
性质3:如果事件A与事件B互斥,那么P(A∪B)=______________.
≥
1
0
P(A)+P(B)
性质4:如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=____________.
性质5:如果A B,那么P(A)≤P(B),由该性质可得,对于任意事件A,因为 A Ω,所以0≤P(A)≤1.
性质6:设A,B是一个随机试验中的两个事件,我们有P(A∪B)=P(A)+P(B)-P(A∩B).
1-P(B)
2.从集合的角度理解互斥事件和对立事件
(1)几个事件彼此互斥,是指由各个事件所含的结果组成的集合的交集为空集.
(2)事件A的对立事件所含的结果组成的集合,是全集中由事件A所含的结果组成的集合的补集.
3.概率加法公式的推广
当一个事件包含多个结果且各个结果彼此互斥时,要用到概率加法公式的推广,即
P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
[典例4] 经统计,在某储蓄所一个营业窗口等候的人数相应的概率如下:
排队人数 0 1 2 3 4 5人及5人以上
概率 0.1 0.16 0.3 0.3 0.1 0.04
求:(1)至多2人排队等候的概率;
(2)至少3人排队等候的概率.
[解] 记“无人排队等候”为事件A,“1人排队等候”为事件B,“2人排队等候”为事件C,“3人排队等候”为事件D,“4人排队等候”为事件E,“5人及5人以上排队等候”为事件F,则事件A,B,C,D,E,F彼此互斥.
(1)记“至多2人排队等候”为事件G,则G=A+B+C,所以P(G)=P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)法一:记“至少3人排队等候”为事件H,则H=D+E+F,
所以P(H)=P(D+E+F)=P(D)+P(E)+P(F)=0.3+0.1+0.04=0.44.
法二:记“至少3人排队等候”为事件H,则其对立事件为事件G,所以P(H)=1-P(G)=0.44.
反思领悟 求复杂的互斥事件的概率的两种方法
(1)直接求解法,将所求事件的概率分解为一些彼此互斥的事件的概率的和,运用互斥事件的概率求和公式计算.
(2)间接求解法,先求此事件的对立事件的概率,再用公式P(A)=1-P(),即运用逆向思维(正难则反).特别是“至多”“至少”型题目,用间接求解法就显得较简便.
巩固迁移4 某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C.求:
(1)P(A),P(B),P(C);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
[解] (1)P(A)=,P(B)==,P(C)==.
(2)因为事件A,B,C两两互斥,所以P(A∪B∪C)=P(A)+P(B)+
P(C)==.故1张奖券的中奖概率为.
(3)设“1张奖券不中特等奖且不中一等奖”为事件N,由对立事件概
率公式得P(N)=1-P(A+B)=1-=.故1张奖券不中特等奖且不中一等奖的概率为.
随堂练习
√
1.(人教A版必修第二册P235练习T2改编)掷一枚质地均匀的骰子,“向上的点数是1或3”为事件A,“向上的点数是1或5”为事件B,则( )
A.A∪B表示向上的点数是1或3或5
B.A=B
C.A∪B表示向上的点数是1或3
D.A∩B表示向上的点数是1或5
A [设A={1,3},B={1,5},则A∩B={1},A∪B={1,3,5},∴A≠B,A∩B表示向上的点数是1,A∪B表示向上的点数是1或3或5.]
2.随着互联网的普及,网上购物已逐渐成为消费时尚,为了解消费者对网上购物的满意情况,某公司随机对4 500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如表:
满意情况 不满意 比较满意 满意 非常满意
人数 200 n 2 100 1 000
√
根据表中数据,估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是( )
A. B. C. D.
C [由题意知n=4 500-200-2 100-1 000=1 200,所以在网上购物的消费者群体中对网上购物“比较满意”或“满意”的总人数为1
200+2 100=3 300,所以在网上购物的消费者群体中对网上购物“比较满意”或“满意”的频率为=.由此估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是.]
3.(2024·福州台江区期末)从装有3个黄球和4个蓝球的口袋内任取3个球,那么互斥不对立的事件是( )
A.恰有一个黄球与恰有一个蓝球
B.至少有一个黄球与都是黄球
C.至少有一个黄球与都是蓝球
D.至少有一个黄球与至少有一个蓝球
√
A [从装有3个黄球和4个蓝球的口袋内任取3个球,不同的取球情况共有以下4种:
①3个球全是黄球;②2个黄球和1个蓝球;③1个黄球和2个蓝球;④3个球全是蓝球.
对于A,恰有一个黄球是情况③,恰有一个蓝球是情况②,
∴恰有一个黄球与恰有一个蓝球是互斥不对立的事件,故A正确;
对于B,至少有一个黄球是情况①②③,都是黄球是情况①,
∴至少有一个黄球与都是黄球能同时发生,不是互斥事件,故B错误;
对于C,至少有一个黄球是情况①②③,都是蓝球是情况④,
∴至少有一个黄球与都是蓝球是对立事件,故C错误;
对于D,至少有一个黄球是情况①②③,至少有一个蓝球是情况②③④,
∴至少有一个黄球与至少有一个蓝球能同时发生,不是互斥事件,故D错误.
故选A.]
4.(2024·绍兴越城区期末)从含有6件次品的50件产品中任取4件,观察其中次品数,这个试验的样本空间Ω=_______________.
{0,1,2,3,4} [取出的4件产品中,最多有4件次品,最少是没有次品.
所以样本空间Ω={0,1,2,3,4}.]
{0,1,2,3,4}
【教用·备选题】
1.(2024·达州期末)将两枚质地均匀的骰子同时投掷,设事件A=“两枚骰子掷出点数均为偶数”,若连续投掷100次,则事件A发生的频数为( )
A.20 B.25
C.50 D.无法确定
√
D [任意一次随机试验中,随机事件的发生具有随机性,即频率(频数与试验次数的比值)具有随机性,而随试验次数的增加,事件发生的频率逐渐稳定于概率,具有稳定性,
则投掷100次的试验中,事件A发生的频率有随机性,故无法确定.故选D.]
2.(2024·安庆大观区期末)设A,B是一个随机试验中的两个事件且P(A)=,P()=,P(B+A)=,则P(B)=( )
A. B.
C. D.
√
A [因为P(A)=,P()=,P(B)=,
因为B·A)=0,
所以P()=P(B)-P(AB)+P(A)-P(AB)
=-2P(AB)=,故P(AB)=,故P(B)=P(B)-P(AB)==.
故选A.]
3.(2024·乌鲁木齐期末)在一个不透明的纸盒中装有6个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.8附近,则袋子中红球约有________个.
24 [设袋子中红球约有x个,利用频率的稳定值来估算概率,
则=0.8,
解得x=24,即袋子中红球约有24个.]
24
4.(2020·全国Ⅰ卷)某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 A B C D
频数 40 20 20 20
乙分厂产品等级的频数分布表
等级 A B C D
频数 28 17 34 21
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
[解] (1)由试加工产品等级的频数分布表知,
甲分厂加工出来的一件产品为A级品的概率的估计值为=0.4;
乙分厂加工出来的一件产品为A级品的概率的估计值为=0.28.
(2)由数据知甲分厂加工出来的100件产品利润的频数分布表为
利润 65 25 -5 -75
频数 40 20 20 20
因此甲分厂加工出来的100件产品的平均利润为
=15.
由数据知乙分厂加工出来的100件产品利润的频数分布表为
利润 70 30 0 -70
频数 28 17 34 21
因此乙分厂加工出来的100件产品的平均利润为
=10.
比较甲、乙两分厂加工的产品的平均利润,厂家应选甲分厂承接加工业务.
课后习题(六十二) 随机事件、频率与概率
1.(多选)(人教A版必修第二册P235练习T2改编)将一枚质地均匀的骰子向上抛掷一次,设事件A=“向上的一面出现奇数点”,事件B=“向上的一面出现的点数不超过2”,事件C=“向上的一面出现的点数不小于4”,则下列说法中正确的有( )
A.B=
B.C= “向上的一面出现的点数大于3”
C.AC= “向上的一面出现的点数不小于3”
D.AC= “向上的一面出现的点数为2”
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
BC [由题意知事件A包含的样本点:向上的一面出现的点数为1,3,5;事件B包含的样本点:向上的一面出现的点数为1,2;事件C包含的样本点:向上的一面出现的点数为4,5,6,所以B=“向上的一面出现的点数为2”,故A错误;C=“向上的一面出现的点数为4或5或6”,故B正确;AC=“向上的一面出现的点数为3或4或5或6”,故C正确;AC=“向上的一面出现的点数为5”,故D错误.故选BC.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(人教A版必修第二册P257练习T1,T2改编)下列说法正确的是( )
A.甲、乙两人做游戏:甲、乙两人各写一个数字,若都是奇数或都是偶数,则甲胜,否则乙胜,这个游戏公平
B.做n次随机试验,事件A发生的频率就是事件A发生的概率
C.某地发行福利彩票,回报率为47%,某人花了100元买该福利彩票,一定会有47元的回报
D.有甲、乙两种报纸可供某人订阅,事件B=“某人订阅甲报纸”是必然事件
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [对于A,甲、乙两人各写一个数字,所有可能的结果为(奇,偶),
(奇,奇),(偶,奇),(偶,偶),则都是奇数或都是偶数的概率为,故游
戏是公平的;
对于B,随着试验次数的增加,频率偏离概率很大的可能性会越来越小,故事件A发生的频率就是事件A发生的概率是不正确的;
对于C,某人花100元买福利彩票,中奖或者不中奖都有可能,但事先无法预料,故C不正确;
对于D,事件B可能发生也可能不发生,故事件B是随机事件,故D不正确.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(苏教版必修第二册P292练习T1改编)某人射击一次,设事件A=“击中环数小于8”,事件B=“击中环数大于8”,事件C=“击中环数不小于8”,事件D=“击中环数不大于9”,则下列说法正确的是( )
A.A和B为对立事件
B.B和C为互斥事件
C.A和C为对立事件
D.B和D为互斥事件
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [由题意,事件A=“击中环数小于8”与事件B=“击中环数大于8”是互斥事件但不是对立事件,故A选项错误;事件B=“击中环数大于8”与事件C=“击中环数不小于8”,能同时发生,所以不是互斥事件,故B选项错误;事件A=“击中环数小于8”与事件C=“击中环数不小于8”是对立事件,故C选项正确;事件B=“击中环数大于8”与事件D=“击中环数不大于9”能同时发生,不是互斥事件,故D选项错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版必修第二册P256例1改编)一个四面体的四个面上分别标记1,2,3,4,重复抛掷这个四面体100次,记录每个面落在桌面的次数(如表).如果再抛掷一次,估计标记3的面落在桌面上的概率为________.
落在桌面上的面 1 2 3 4
频数 19 23 22 36
0.22
题号
1
3
5
2
4
6
8
7
9
10
11
12
0.22 [由题表知,标记3的面落在桌面上的频率为=0.22,故其概率的估计值为0.22.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·上海普陀区模拟)从放有两个红球、一个白球的袋子中一次任意取出两个球,两个红球分别标记为A,B,白球标记为C,则它的一个样本空间可以是( )
A.{AB,BC}
B.{AB,AC,BC}
C.{AB,BA,BC,CB}
D.{AB,BA,AC,CA,CB}
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [两个红球分别标记为A,B,白球标记为C,
则一次任意取出两个球的情况为AB,AC,BC,即它的一个样本空间可以是{AB,AC,BC}.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·西宁期末)有一个人在打靶中,连续射击2次,事件“至少有1次中靶”的对立事件是( )
A.至多有1次中靶 B.2次都中靶
C.2次都不中靶 D.只有1次中靶
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [由于两个事件互为对立事件时,这两件事不能同时发生,且这两件事的和事件是一个必然事件,
再由于一个人在打靶中,连续射击2次,事件“至少有1次中靶”的反面为“2次都不中靶”,故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2024·长治期末)下列说法正确的是( )
A.甲、乙两人进行羽毛球比赛,甲胜的概率为,则比赛4场,甲一定胜3场
B.概率是随机的,在试验前不能确定
C.事件A,B满足A B,则P(A)<P(B)
D.天气预报中,预报明天降水概率为90%,是指降水的可能性是90%
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
D [对于A,甲、乙两人比赛,甲胜的概率为,是指每场比赛,甲胜的可能性为,
则比赛4场,甲可能胜4场、3场、2场、1场、0场,故A错误;
对于B,随机试验的频率是变化的,概率是频率的稳定值,是固定的,故B错误;
对于C,事件A,B满足A B,则P(A)≤P(B),故C错误;
对于D,天气预报中,预报明天降水概率为90%,是指降水的可能性是90%,故D正确.
故选D.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2024·烟台期末)若事件A与B互为对立事件,且P(A)=0.4,则P(B)=( )
A.0 B.0.4
C.0.6 D.1
√
C [由对立事件的概率公式,得P(B)=1-P(A)=0.6.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·重庆期末)已知两个互斥事件A,B满足P(A+B)=0.5,P(A)=0.2,则P(B)=( )
A.0.4 B.0.3
C.0.6 D.0.1
√
B [因为A,B为互斥事件,
P(A+B)=0.5,P(A)=0.2,
所以P(B)=0.5-0.2=0.3.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(多选)(2024·溧阳市期末)某篮球运动员进行投篮训练,连续投篮两次,设事件A表示随机事件“两次都投中”,事件B表示随机事件“两次都未投中”,事件C表示随机事件“恰有一次投中”,事件D表示随机事件“至少有一次投中”,则下列关系正确的是( )
A.A D B.B∩D=
C.A∪B=B∪D D.A∪C=D
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
ABD [事件A表示“两次都投中”;事件B表示“两次都未投中”;事件C表示“恰有一次投中”;事件D表示“至少有一次投中”,即表示“两次都投中”或“恰有一次投中”.
A:事件A表示“两次都投中”,事件D表示“至少有一次投中”,故A D,故A正确;
B:事件B和事件D是对立事件,故B∩D= ,故B正确;
C:事件A∪B表示“两次都投中”或“两次都未投中”,
而事件B∪D表示“两次都未投中”“两次都投中”或“恰有一次投中”,故C错误;
D:事件A∪C表示“两次都投中”或“恰有一次投中”,故A∪C=D,故D正确.
故选ABD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·太原期末)投掷两枚质地均匀的硬币,用ai表示“第i枚硬币正面朝上”,bi表示“第i枚硬币反面朝上”(i=1,2),则该试验的样本空间Ω=____________________________________.
{(a1,a2),(a1,b2),(b1,a2),(b1,b2)} [由题意可知,该试验的样本空间Ω={(a1,a2),(a1,b2),(b1,a2),(b1,b2)}.]
{(a1,a2),(a1,b2),(b1,a2),(b1,b2)}
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·荆州调考)某河流上的一座水力发电站,每年六月的发电量Y(单位:万千瓦时)与该河上游在六月份的降雨量X(单位:毫米)有关.据统计,当X=70时,Y=460;X每增加10,Y增加5.已知近20年X的值为140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的频率分布表:
近20年六月份降雨量频率分布表
降雨量 70 110 140 160 200 220
频率
(2)假定每年六月份的降雨量与近20年六月份降雨量的分布规律相同,并将频率视为概率,求明年六月份该水力发电站的发电量低于490万千瓦时或超过530万千瓦时的概率.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)在所给数据中,降雨量为110毫米的有3个,降雨量为160毫米的有7个,降雨量为200毫米的有3个.
故近20年六月份降雨量频率分布表为
降雨量 70 110 140 160 200 220
频率
(2)根据题意,Y=460+×5=+425,故P(“发电量低于490万千瓦时或超过530万千瓦时”)=P(Y<490或Y>530)=P(X<130或X>210)=P(X=70)+P(X=110)+P(X=220)==.
故明年六月份该水力发电站的发电量低于490万千瓦时或超过530万千瓦时的概率为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
同课章节目录
