《高考快车道》2026版高三一轮总复习数学(基础版)105 第九章 第7课时 离散型随机变量及其分布列、数字特征 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)105 第九章 第7课时 离散型随机变量及其分布列、数字特征 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:02 | ||
图片预览










文档简介
(共86张PPT)
第九章 计数原理、概率、随机变量及其分布
第7课时 离散型随机变量及其分布列、数字特征
[考试要求] 1.理解取有限个值的离散型随机变量及其分布列的概念.
2.理解并会求离散型随机变量的数字特征.
考点一 离散型随机变量的分布列概念及性质
1.随机变量的有关概念
(1)随机变量:一般地,对于随机试验样本空间Ω中的每个样本点ω,都有____的实数X(ω)与之对应,我们称X为随机变量.
(2)离散型随机变量:可能取值为有限个或可以________的随机变量.
提醒:若X是随机变量,则Y=aX+b(a,b为常数)也是随机变量.
唯一
一一列举
2.离散型随机变量的分布列及性质
(1)一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P(X=xi)=pi,i=1,2,…,n为X的概率分布列,简称分布列.
(2)离散型随机变量分布列的性质
①pi__0,i=1,2,…,n;
②p1+p2+…+pn=__.
≥
1
[典例1] (1)(多选)已知随机变量X的分布列如表(其中a为常数):
√
X 0 1 2 3 4
P 0.1 0.2 0.4 0.2 a
则下列计算结果正确的是( )
A.a=0.1 B.P(X≤2)=0.7
C.P(X≥3)=0.4 D.P(X≤1)=0.3
√
√
(2)离散型随机变量X的概率分布规律为P(X=n)=(n=1,2,3,4),其中a是常数,则P=( )
A. B.
C. D.
√
(1)ABD (2)D [(1)因为0.1+0.2+0.4+0.2+a=1,解得a=0.1,故A正确;
由分布列知P(X≤2)=P(X=0)+P(X=1)+P(X=2)=0.1+0.2+0.4=0.7,故B正确;
P(X≥3)=P(X=3)+P(X=4)=0.2+0.1=0.3,故C错误;
P(X≤1)=P(X=0)+P(X=1)=0.1+0.2=0.3,故D正确.
(2)因为P(X=n)=(n=1,2,3,4),
所以=1,那么a=,
所以P=P(X=1)+P(X=2)==.]
反思领悟 (1)本例中,利用“概率之和为1”可以求相关参数的值,如本例(1)(2)中求a即是如此.
(2)利用“在某个范围内的概率等于它取这个范围内各个值的概率之和”求某些特定事件的概率,如本例(1)中,P(X≤2)=P(X=0)+P(X
=1)+P(X=2)等,本例(2)中P=P(X=1)+P(X=2)等.
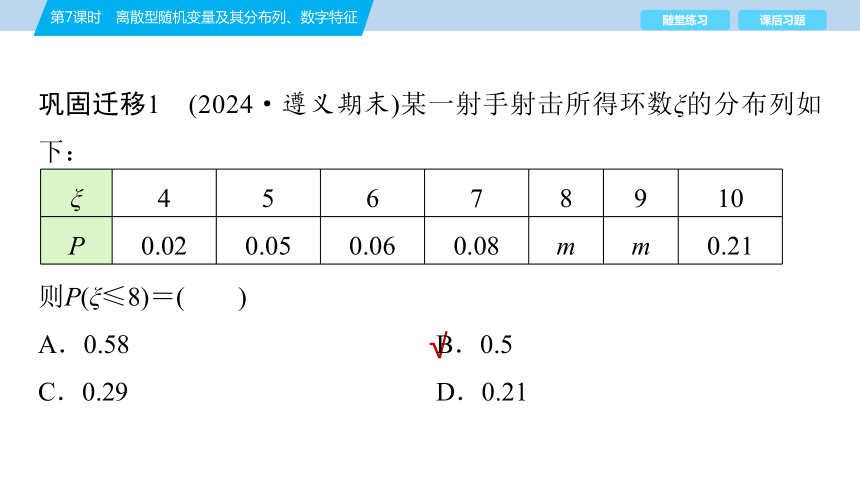
巩固迁移1 (2024·遵义期末)某一射手射击所得环数ξ的分布列如下:
ξ 4 5 6 7 8 9 10
P 0.02 0.05 0.06 0.08 m m 0.21
√
则P(ξ≤8)=( )
A.0.58 B.0.5
C.0.29 D.0.21
B [由离散型随机变量分布列的性质可知,0.02+0.05+0.06+0.08+m+m+0.21=1,解得m=0.29,
故P(ξ≤8)=1-P(ξ=9)-P(ξ=10)=1-0.29-0.21=0.5.故选B.]
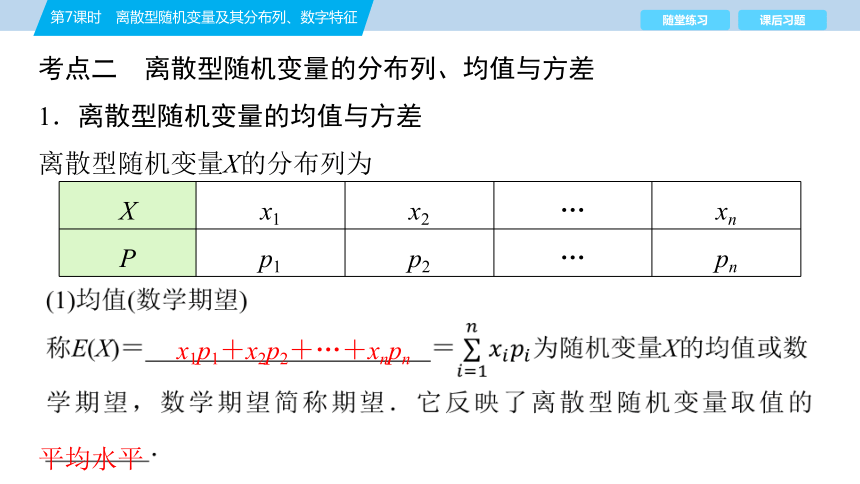
考点二 离散型随机变量的分布列、均值与方差
1.离散型随机变量的均值与方差
离散型随机变量X的分布列为
X x1 x2 … xn
P p1 p2 … pn
(1)均值(数学期望)
称E(X)=______________________=为随机变量X的均值或数
学期望,数学期望简称期望.它反映了离散型随机变量取值的________.
x1p1+x2p2+…+xnpn
平均水平
(2)方差
为随机变量 的方差,可以用来度量随机变量
取值与其均值E(X)的________,并称为随机变量X的标准差,记为σ(X).
(xi-E(x))2pi
偏离程度
2.均值与方差的性质
(1)E(aX+b)=______________.(a,b为常数)
(2)D(aX+b)=____________.(a,b为常数)
aE(x)+b
a2D(x)
[常用结论]
(1)E(X)=X,D(X)=0,其中X为常数.
(2)E(X1+X2)=E(X1)+E(X2).
(3)D(X)=E(X2)-(E(X))2.
考向1 离散型随机变量的分布列及数字特征
[典例2] (1)(多选)(2024·临夏州期末)离散型随机变量X的分布列如表所示,则( )
√
X 0 1 2 4
P a
A.a= B.P(X<2)=
C.E(X)=2 D.D(X)=
√
√
(2)已知某离散型随机变量X的分布列如表:
X -1 0 1 2
P a b c
若E(X)=,P(X≥1)=,则D(X)=( )
A. B.
C. D.
√
(1)ACD (2)C [(1)A选项,由题意得,+a+=1,解得a=,A正确;
B选项,P(X<2)=P(X=0)+P(X=1)==,B错误;
C选项,E(X)=0×+1×+2×+4×=2,C正确;
D选项,D(X)=(0-2)2×+(1-2)2×+(2-2)2×+(4-2)2×=,D
正确.
故选ACD.
(2)由题意,得a+b+c=1-=,①
由E(X)=(-1)×a+0×b+1×c+2×=,得-a+c=,②
由P(X≥1)=P(X=1)+P(X=2)=c+=,得c=,
代入①②解得a=,b=,
所以D(X)==.故选C.]
反思领悟 本例(1)这种一般的离散型随机变量均值与方差的计算,只需分清数据、选择公式、代入计算即可;本例(2)由概率、期望(均值)求参数,要依据条件利用概率、期望公式列出含有参数的方程(组),解方程(组)即可求出参数值.
巩固迁移2 (1)(人教A版选择性必修第三册P66练习T1改编)已知随机变量X的分布列为
X -1 0 1
P
√
设Y=2X+3,则E(Y)的值为( )
A. B.4
C.-1 D.1
(2)已知随机变量X的分布列如表:
X a 2 3 4
P b
若E(X)=2,则a=________,D(X)=________.
0
(1)A (2)0 [(1)E(X)=-1×+0×+1×=-,E(Y)=E(2X+3)=2E(X)+3=-+3=.故选A.
(2)由题意知,+b+=1,所以b=.
又E(X)=a×+2×+3×+4×=2,解得a=0,所以D(X)=(0-2)2×+(2-2)2×+(3-2)2×+(4-2)2×=.]
考向2 均值(数学期望)与方差的性质应用
[典例3] 设随机变量X的分布列为P(X=k)=(k=1,2,5),a∈R,E(X),D(X)分别为随机变量X的均值与方差,则下列结论正确的是( )
A.P(0C.D(X)=2 D.D(3X+1)=6
√
C [因为随机变量X的分布列为P(X=k)=(k=1,2,5),
由分布列的性质可知,P(X=1)+P(X=2)+P(X=5)==1,
解得a=1.
P(0因为E(X)=1×+2×+5×=2,
所以E(3X+2)=3E(X)+2=3×2+2=8,故B不正确;
由D(X)=×(1-2)2+×(2-2)2+×(5-2)2=2,故C正确;
因为D(X)=2,
所以D(3X+1)=9D(X)=18,故D不正确.故选C.]
反思领悟 本例中,求E(3X+2)一般有两种方法,(1)定义法:先列出3X+2的分布列,再求E(3X+2);(2)性质法:直接套用公式E(3X+2)=3E(X)+2.求D(3X+1)直接套用公式D(3X+1)=32D(X)=9D(X).
巩固迁移3 已知X的分布列如表所示:
X -1 0 1
P a
(1)求X 2的分布列;
(2)计算X的方差;
(3)若Y=4X+3,求Y的均值和方差.
[解] (1)由分布列的性质知+a=1,
解得a=,所以X2的分布列为
(2)由(1)知a=,
所以E(X)=(-1)×+0×+1×=-,
D(X)==.
(3)因为Y=4X+3,
所以E(Y)=4E(X)+3=2,
D(Y)=42D(X)=11.
X 2 0 1
P
考向3 具体事件的均值与方差
[典例4] 一台设备由三个部件构成,假设在一天的运转中,部件1,2,3需要调整的概率分别为0.1,0.2,0.3,各部件的状态相互独立.
(1)求设备在一天的运转中,部件1,2中至少有1个需要调整的概率;
(2)记设备在一天的运转中需要调整的部件个数为X,求X的分布列、数学期望及方差.
[解] (1)设部件1需要调整为事件A,部件2需要调整为事件B,部件3需要调整为事件C,
由题意可知,P(A)=0.1,P(B)=0.2,P(C)=0.3.
部件1,2中至少有1个需要调整的概率为
1-[1-P(A)][1-P(B)]=1-0.9×0.8=1-0.72=0.28.
(2)由题意可知X的取值为0,1,2,3.
P(X=0)=[1-P(A)][1-P(B)][1-P(C)]=(1-0.1)×(1-0.2)×(1-0.3)=0.504,P(X=1)=P(A)[1-P(B)][1-P(C)]+[1-P(A)]P(B)[1-P(C)]+[1-P(A)][1-P(B)]P(C)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398,P(X=2)=P(A)P(B)[1-P(C)]+P(A)[1-P(B)]P(C)+[1-P(A)]P(B)P(C)
=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092,
P(X=3)=P(A)P(B)P(C)=0.1×0.2×0.3=0.006,
故X的分布列为
X 0 1 2 3
P 0.504 0.398 0.092 0.006
所以E(X)=0.504×0+0.398×1+0.092×2+0.006×3=0.6,
D(X)=(0-0.6)2×0.504+(1-0.6)2×0.398+(2-0.6)2×0.092+(3-0.6)2×0.006=0.46.
链接·2025高考试题
(2025·全国一卷)有5个相同的球,分别标有数字1,2,3,4,5,从中有放回地随机取3次,每次取1个球.记X为这5个球中至少被取出1次的球的个数,则X的数学期望E(X)=________.
所以E(X)=1×+2×+3×=.]
X 1 2 3
P
[X的所有可能取值为1,2,3,则P(X=1)===,P(X=2)=×6==,P(X=3)=×6==,所以X的分布列为
反思领悟 本例求均值与方差的关键是确定随机变量的所有可能取值,写出分布列,正确运用均值、方差公式进行计算.
巩固迁移4 甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10 分,负方得0 分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.用X表示乙学校的总得分,求X 的分布列与期望.
[解] 依题可知, X 的可能取值为0,10,20,30,
P(X=0)=0.5×0.4×0.8=0.16,
P(X=10)=0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.44,
P(X=20)=0.5×0.6×0.8+0.5×0.4×0.2+0.5×0.6×0.2=0.34,
P(X=30)=0.5×0.6×0.2=0.06.
所以X的分布列为
X 0 10 20 30
P 0.16 0.44 0.34 0.06
E(X)=0×0.16+10×0.44+20×0.34+30×0.06=13.
考点三 均值与方差在决策中的应用
[典例5] (经典题)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
[解] (1)由已知可得,X的所有可能取值为0,20,100,
P(X=0)=1-0.8=0.2,
P(X=20)=0.8×(1-0.6)=0.32,
P(X=100)=0.8×0.6=0.48,
所以X的分布列为
X 0 20 100
P 0.2 0.32 0.48
(2)由(1)可知当小明先回答A类问题时,E(X)=0×0.2+20×0.32+100×0.48=54.4.
当小明先回答B类问题时,记Y为小明的累计得分,
则Y的所有可能取值为0,80,100,
P(Y=0)=1-0.6=0.4,
P(Y=80)=0.6×(1-0.8)=0.12,
P(Y=100)=0.6×0.8=0.48,
所以Y的分布列为
Y 0 80 100
P 0.4 0.12 0.48
则E(Y)=0×0.4+80×0.12+100×0.48=57.6.
因为57.6>54.4,即E(Y)>E(X),
所以为使累计得分的期望最大,小明应选择先回答B类问题.
反思领悟 随机变量的均值和方差从整体和全局上刻画了随机变量,是生产实际中用于方案取舍的重要理论依据.一般先比较均值,若均值相同,再用方差来决定.
巩固迁移5 有甲、乙两个建材厂,都想投标参加某重点建设项目,为了对重点建设项目负责,政府到两建材厂抽样检查,他们从中各取等量的样本检查它们的抗拉强度指数如表:
X 110 120 125 130 135
P 0.1 0.2 0.4 0.1 0.2
Y 100 115 125 130 145
P 0.1 0.2 0.4 0.1 0.2
其中X和Y分别表示甲、乙两厂材料的抗拉强度,比较甲、乙两厂材料哪一种稳定性好.
[解] E(X)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(Y)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(X)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
D(Y)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165,
由于E(X)=E(Y),D(X)离散型随机变量分布列的求解步骤
[典例] 有编号为1,2,3,4的4个学生,入座编号为1,2,3,4的4个座位,规定每个学生坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为X.求随机变量X的分布列.
[解] 因为学生所坐的座位号与该生的编号不同的学生人数为X,
由题意可知X的可能取值是0,2,3,4,
所以P(X=0)==,P(X=2)==,
P(X=3)==,P(X=4)=1-=,
所以随机变量X的分布列为
X 0 2 3 4
P
反思领悟 求离散型随机变量分布列的关键是求随机变量所取值对应的概率.
应用体验 甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为.记甲同学三个项目中通过考试的个数为X,求随机变量X的分布列.
[解] 随机变量X的所有可能取值为0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==.
所以随机变量X的分布列为
X 0 1 2 3
P
随堂练习
1.(人教A版选择性必修第三册P71习题7.3T3改编)随机变量X的分布列为P(X=0)=0.2,P(X=1)=a,P(X=2)=b,若E(X)=1,则a=________;b=________.
0.6 0.2 [由题意知,
解得]
0.6
0.2
2.(人教A版选择性必修第三册P66练习T1改编)已知随机变量X的分布列为
X 1 2 3 4 5
P 0.1 0.3 0.4 0.1 0.1
则E(X)=________;E(3X+2)=________.
2.8 10.4 [E(X)=1×0.1+2×0.3+3×0.4+4×0.1+5×0.1=2.8,E(3X+2)=3E(X)+2=3×2.8+2=10.4.]
10.4
2.8
3.医学上发现,某种病毒侵入人体后,人的体温会升高.记病毒侵入后人体的平均体温为X ℃.医学统计发现,X的分布列如表所示.
X 37 38 39 40
P 0.1 0.5 0.3 0.1
(1)求出E(X),D(X);
(2)已知人体体温为X ℃时,相当于Y=1.8X+32(℃),求E(Y),D(Y).
[解] (1)由题可得E(X)=37×0.1+38×0.5+39×0.3+40×0.1=38.4,D(X)=(37-38.4)2×0.1+(38-38.4)2×0.5+(39-38.4)2×0.3+(40-38.4)2×0.1=0.64,
(2)由Y=1.8X+32可知,E(Y)=1.8E(X)+32=1.8×38.4+32=101.12,D(Y)=1.82×D(X)=×0.64=2.073 6.
【教用·备选题】
1.(2024·马鞍山期末)随机变量X的分布列如表所示,则D(bX)的最大值为( )
√
X 1 2 3
P a 2b a
A. B.
C. D.
D [由题可知2a+2b=1,即a+b=,
E(X)=a+4b+3a=4(a+b)=2,D(X)=a(1-2)2+(3-2)2a=2a,
则D(bX)=b2D(X)=2ab2=-2b3+b2,
令f (b)=-2b3+b2,则f ′(b)=-6b2+2b=-2b(3b-1),
则f (b)在上单调递增,在上单调递减,
所以f (b)max=f =,则D(bX)的最大值为.
故选D.]
2.(2024·泸州江阳区期末)已知随机变量X的概率分布列为P(X=n)=(n=1,2,3,…,10),则实数a=________.
[随机变量X的概率分布列为P(X=n)=(n=1,2,3,…,10),∴
=1,
∴a=a=1,则实数a=.]
3.(2025·上海普陀模拟)一个盒子里有1个红球和2个绿球,每次拿一个,不放回,拿出红球即停,设拿出绿球的个数为X,则E(X)=__________.
1 [由题意,随机变量X的所有可能取值为0,1,2,
则P(X=0)=;P(X=1)==;P(X=2)==,
所以E(X)=0×+1×+2×=1.]
1
4.(2024·四川雅安高三联考)为了促进消费,某商场针对会员客户推出会员积分兑换商品活动:每位会员客户可在价值80元、90元、100元的A,B,C三种商品中选择一种使用积分进行兑换,每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1 000积分,且甲
兑换A,B,C三种商品的概率分别为,乙兑换A,B,C三种商品的概率分别为,且他们兑换何种商品相互独立.
(1)求甲、乙两人兑换同一种商品的概率;
(2)记X为两人兑换商品后的积分总余额,求X的分布列与期望.
[解] (1)由题可知,甲、乙两人兑换同一种商品的概率为=.
(2)由题意,兑换A,B,C三种商品所需的积分分别为800,900,
1 000,则X的取值可能为0,100,200,300,400,
P(X=0)==,P(X=100)==,
P(X=200)==,
P(X=300)==,
P(X=400)==,
则X的分布列为
X 0 100 200 300 400
P
E(X)=0×+100×+200×+300×+400×=250.
课后习题(六十五) 离散型随机变量及其分布列、数字特征
1.(北师大版选择性必修第一册P202习题6-2A组T3改编)某射击运动员射击所得的环数X的分布列如下表:
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
X 5 6 7 8 9 10
P 0.06 0.06 0.09 a 0.29 0.22
此运动员“射击一次命中的环数大于6且小于9”的概率为( )
A.0.43 B.0.37 C.0.51 D.0.79
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [由分布列的性质知a=1-(0.06+0.06+0.09+0.29+0.22)=0.28.
∴P(6=0.09+0.28=0.37.故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(多选)(人教A版选择性必修第三册P70练习T1改编)设离散型随机变量X的分布列为
X 0 1 2 3 4
P q 0.4 0.1 0.2 0.2
若离散型随机变量Y满足Y=2X+1,则下列结果正确的有( )
A.q=0.1 B.E(X)=2,D(X)=1.4
C.E(X)=2,D(X)=1.8 D.E(Y)=5,D(Y)=7.2
√
√
ACD [由离散型随机变量X的分布列的性质得:
q=1-0.4-0.1-0.2-0.2=0.1,
E(X)=0×0.1+1×0.4+2×0.1+3×0.2+4×0.2=2,
D(X)=(0-2)2×0.1+(1-2)2×0.4+(2-2)2×0.1+(3-2)2×0.2+(4-2)2×0.2=1.8,
∵离散型随机变量Y满足Y=2X+1,
∴E(Y)=2E(X)+1=5,D(Y)=4D(X)=7.2.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(多选)(苏教版选择性必修第二册P115练习T2改编)设随机变量ξ的
分布列为P=ak(k=1,2,3,4,5),则( )
A.a= B.P=
C.P= D.P(ξ=1)=
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AB [对于选项A,∵随机变量ξ的分布列为P=ak(k=1,2,3,4,5),∴P+P+P+P+P(ξ=1)=a+2a+3a+4a+5a=1,解得a=,故A正确;对于选项B,=P=3×=,故B正确;对于选项C,P=P+P=+2×=,故C错误;对于选项D,P(ξ=1)=5×=,故D错误.故选AB.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第三册P68方差公式简化计算改编)已知离散型随机变量X的取值为有限个,E(X)=,D(X)=,则E(X2)=________.
[因为E(X)=,D(X)=,由D(X)=E(X 2)-(E(X))2,
得E(X 2)=D(X)+(E(X))2==.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·重庆长寿区期末)设随机变量X的概率分布列为
√
X 1 2 3 4
P m
则P(|X-3|=1)=( )
A. B. C.D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [由题意得+m+=1,解得m=,
随机变量X的概率分布列为
X 1 2 3 4
P
∴P(|X-3|=1)=P(X=2)+P(X=4)=,故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·眉山仁寿县期末)已知随机变量X的分布列为
X 0 1 2
P m
若Y=3X-2,则E(Y)=( )
A. B.
C.- D.-
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [由题可知+m=1,解得m=,
则E(X)=0×+1×+2×=,
所以E(Y)=3E(X)-2=3×-2=.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2025·湖北咸宁模拟)设0√
X 0 a 1
P
则当a在(0,1)内减小时( )
A.D(X)减小 B.D(X)增大
C.D(X)先减小后增大 D.D(X)先增大后减小
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [根据题意可得,E(X)==,
D(X)===,
所以D(X)在上单调递减,在上单调递增,所以D(X)先减小后增大.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·四川攀枝花月考)已知正数a,b,c成等差数列,且随机变量X的分布列为
√
X 1 2 3
P a b c
下列选项正确的是( )
A.b= B.a+c=
C.√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
BCD [正数a,b,c成等差数列,则a+c=2b,
又由分布列的性质可知,a+b+c=1,
解得故A错误,B正确;
由a+c=,得0则E(X)=a+2b+3c=2c+∈,C正确;
D(X)=a++c=++c=-4c2+c+=
-4+,
当c=时,D(X)取得最大值,且最大值为,D正确.
故选BCD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·重庆沙坪坝区月考)已知随机变量ξ,D(10ξ)=,则ξ的标准差为________.
[∵D(10ξ)=100D(ξ)=,∴D(ξ)=,
∴ξ的标准差==.
∴ξ的标准差为.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·保定模拟)已知随机变量X的所有可能取值为1,2,3,其分布列为
X 1 2 3
P P1 P2 P3
若E(X)=,则P3-P1=________.
-
题号
1
3
5
2
4
6
8
7
9
10
11
12
- [因为E(X)=P1+2P2+3P3=,①
且P1+P2+P3=1,②
所以①-②×2可得,P1+2P2+3P3-2(P1+P2+P3)=P3-P1=-.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·广州开学考试节选)某公司拟通过摸球中奖的方式对员工发放节日红包.在一个不透明的袋子中装有n个形状大小相同的标有面值的球,每位员工从球袋中一次性随机摸取m个球(m≤n),摸完后全部放回袋中,球上所标的面值之和为该员工所获得的红包数额.
若n=5,m=4,当袋中的球中有1个所标面值为10元,2个为20元,1个为30元,1个为40元时,求员工所获得红包数额的数学期望与方差.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 设X为员工获得的红包数额,则X可能取值为80,90,100,110,
所以P(X=80)==,P(X=90)==,
P(X=100)==,P(X=110)==,
所以E(X)=80×+90×+100×+110×=96,
D(X)=(80-96)2×+(90-96)2×+(100-96)2×+(110-96)2×=
104.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·山东潍坊高三模拟)某投资公司对以下两个项目进行前期市场调研.项目A:通信设备.根据调研,投资到该项目上,所有可能结果为获利40%,损失20%,不赔不赚,且这三种情况发生的概率分别为,a.项目B:新能源汽车.根据调研,投资到该项目上,所有可能结果为获利30%,亏损10%,且这两种情况发生的概率分别为b,c.经测算,当投入A,B两个项目的资金相等时,它们所获利润的均值也相等.
(1)求a,b,c的值;
(2)若将100万元全部投到其中的一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合适的项目.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)依题意,得+a=1, 所以a=.
设投入项目A,B的资金都为x万元,随机变量X1和X2分别表示投资项目A和B所获的利润,则X1和X2的分布列分别为
X1 0.4x -0.2x 0
P
X2 0.3x -0.1x
P b c
由分布列得E(X1)=0.4x×+(-0.2x)×+0×=0.2x,
E(X2)=0.3bx-0.1cx.
因为E(X1)=E(X2),所以0.3bx-0.1cx=0.2x,
即0.3b-0.1c=0.2.
又b+c=1,解得b=,c=.
所以a=,b=,c=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)当投入100万元资金时,
由(1)知x=100,
所以E(X1)=E(X2)=20,
D(X1)=(40-20)2×+(-20-20)2×+(0-20)2×=600,
D(X2)=(30-20)2×+(-10-20)2×=300.
所以D(X1)>D(X2),这说明虽然项目A和项目B的平均收益相等,但项目B更稳妥,所以从投资回报稳定性的角度考虑,建议该投资公司选择项目B.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
第九章 计数原理、概率、随机变量及其分布
第7课时 离散型随机变量及其分布列、数字特征
[考试要求] 1.理解取有限个值的离散型随机变量及其分布列的概念.
2.理解并会求离散型随机变量的数字特征.
考点一 离散型随机变量的分布列概念及性质
1.随机变量的有关概念
(1)随机变量:一般地,对于随机试验样本空间Ω中的每个样本点ω,都有____的实数X(ω)与之对应,我们称X为随机变量.
(2)离散型随机变量:可能取值为有限个或可以________的随机变量.
提醒:若X是随机变量,则Y=aX+b(a,b为常数)也是随机变量.
唯一
一一列举
2.离散型随机变量的分布列及性质
(1)一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P(X=xi)=pi,i=1,2,…,n为X的概率分布列,简称分布列.
(2)离散型随机变量分布列的性质
①pi__0,i=1,2,…,n;
②p1+p2+…+pn=__.
≥
1
[典例1] (1)(多选)已知随机变量X的分布列如表(其中a为常数):
√
X 0 1 2 3 4
P 0.1 0.2 0.4 0.2 a
则下列计算结果正确的是( )
A.a=0.1 B.P(X≤2)=0.7
C.P(X≥3)=0.4 D.P(X≤1)=0.3
√
√
(2)离散型随机变量X的概率分布规律为P(X=n)=(n=1,2,3,4),其中a是常数,则P=( )
A. B.
C. D.
√
(1)ABD (2)D [(1)因为0.1+0.2+0.4+0.2+a=1,解得a=0.1,故A正确;
由分布列知P(X≤2)=P(X=0)+P(X=1)+P(X=2)=0.1+0.2+0.4=0.7,故B正确;
P(X≥3)=P(X=3)+P(X=4)=0.2+0.1=0.3,故C错误;
P(X≤1)=P(X=0)+P(X=1)=0.1+0.2=0.3,故D正确.
(2)因为P(X=n)=(n=1,2,3,4),
所以=1,那么a=,
所以P=P(X=1)+P(X=2)==.]
反思领悟 (1)本例中,利用“概率之和为1”可以求相关参数的值,如本例(1)(2)中求a即是如此.
(2)利用“在某个范围内的概率等于它取这个范围内各个值的概率之和”求某些特定事件的概率,如本例(1)中,P(X≤2)=P(X=0)+P(X
=1)+P(X=2)等,本例(2)中P=P(X=1)+P(X=2)等.
巩固迁移1 (2024·遵义期末)某一射手射击所得环数ξ的分布列如下:
ξ 4 5 6 7 8 9 10
P 0.02 0.05 0.06 0.08 m m 0.21
√
则P(ξ≤8)=( )
A.0.58 B.0.5
C.0.29 D.0.21
B [由离散型随机变量分布列的性质可知,0.02+0.05+0.06+0.08+m+m+0.21=1,解得m=0.29,
故P(ξ≤8)=1-P(ξ=9)-P(ξ=10)=1-0.29-0.21=0.5.故选B.]
考点二 离散型随机变量的分布列、均值与方差
1.离散型随机变量的均值与方差
离散型随机变量X的分布列为
X x1 x2 … xn
P p1 p2 … pn
(1)均值(数学期望)
称E(X)=______________________=为随机变量X的均值或数
学期望,数学期望简称期望.它反映了离散型随机变量取值的________.
x1p1+x2p2+…+xnpn
平均水平
(2)方差
为随机变量 的方差,可以用来度量随机变量
取值与其均值E(X)的________,并称为随机变量X的标准差,记为σ(X).
(xi-E(x))2pi
偏离程度
2.均值与方差的性质
(1)E(aX+b)=______________.(a,b为常数)
(2)D(aX+b)=____________.(a,b为常数)
aE(x)+b
a2D(x)
[常用结论]
(1)E(X)=X,D(X)=0,其中X为常数.
(2)E(X1+X2)=E(X1)+E(X2).
(3)D(X)=E(X2)-(E(X))2.
考向1 离散型随机变量的分布列及数字特征
[典例2] (1)(多选)(2024·临夏州期末)离散型随机变量X的分布列如表所示,则( )
√
X 0 1 2 4
P a
A.a= B.P(X<2)=
C.E(X)=2 D.D(X)=
√
√
(2)已知某离散型随机变量X的分布列如表:
X -1 0 1 2
P a b c
若E(X)=,P(X≥1)=,则D(X)=( )
A. B.
C. D.
√
(1)ACD (2)C [(1)A选项,由题意得,+a+=1,解得a=,A正确;
B选项,P(X<2)=P(X=0)+P(X=1)==,B错误;
C选项,E(X)=0×+1×+2×+4×=2,C正确;
D选项,D(X)=(0-2)2×+(1-2)2×+(2-2)2×+(4-2)2×=,D
正确.
故选ACD.
(2)由题意,得a+b+c=1-=,①
由E(X)=(-1)×a+0×b+1×c+2×=,得-a+c=,②
由P(X≥1)=P(X=1)+P(X=2)=c+=,得c=,
代入①②解得a=,b=,
所以D(X)==.故选C.]
反思领悟 本例(1)这种一般的离散型随机变量均值与方差的计算,只需分清数据、选择公式、代入计算即可;本例(2)由概率、期望(均值)求参数,要依据条件利用概率、期望公式列出含有参数的方程(组),解方程(组)即可求出参数值.
巩固迁移2 (1)(人教A版选择性必修第三册P66练习T1改编)已知随机变量X的分布列为
X -1 0 1
P
√
设Y=2X+3,则E(Y)的值为( )
A. B.4
C.-1 D.1
(2)已知随机变量X的分布列如表:
X a 2 3 4
P b
若E(X)=2,则a=________,D(X)=________.
0
(1)A (2)0 [(1)E(X)=-1×+0×+1×=-,E(Y)=E(2X+3)=2E(X)+3=-+3=.故选A.
(2)由题意知,+b+=1,所以b=.
又E(X)=a×+2×+3×+4×=2,解得a=0,所以D(X)=(0-2)2×+(2-2)2×+(3-2)2×+(4-2)2×=.]
考向2 均值(数学期望)与方差的性质应用
[典例3] 设随机变量X的分布列为P(X=k)=(k=1,2,5),a∈R,E(X),D(X)分别为随机变量X的均值与方差,则下列结论正确的是( )
A.P(0
√
C [因为随机变量X的分布列为P(X=k)=(k=1,2,5),
由分布列的性质可知,P(X=1)+P(X=2)+P(X=5)==1,
解得a=1.
P(0
所以E(3X+2)=3E(X)+2=3×2+2=8,故B不正确;
由D(X)=×(1-2)2+×(2-2)2+×(5-2)2=2,故C正确;
因为D(X)=2,
所以D(3X+1)=9D(X)=18,故D不正确.故选C.]
反思领悟 本例中,求E(3X+2)一般有两种方法,(1)定义法:先列出3X+2的分布列,再求E(3X+2);(2)性质法:直接套用公式E(3X+2)=3E(X)+2.求D(3X+1)直接套用公式D(3X+1)=32D(X)=9D(X).
巩固迁移3 已知X的分布列如表所示:
X -1 0 1
P a
(1)求X 2的分布列;
(2)计算X的方差;
(3)若Y=4X+3,求Y的均值和方差.
[解] (1)由分布列的性质知+a=1,
解得a=,所以X2的分布列为
(2)由(1)知a=,
所以E(X)=(-1)×+0×+1×=-,
D(X)==.
(3)因为Y=4X+3,
所以E(Y)=4E(X)+3=2,
D(Y)=42D(X)=11.
X 2 0 1
P
考向3 具体事件的均值与方差
[典例4] 一台设备由三个部件构成,假设在一天的运转中,部件1,2,3需要调整的概率分别为0.1,0.2,0.3,各部件的状态相互独立.
(1)求设备在一天的运转中,部件1,2中至少有1个需要调整的概率;
(2)记设备在一天的运转中需要调整的部件个数为X,求X的分布列、数学期望及方差.
[解] (1)设部件1需要调整为事件A,部件2需要调整为事件B,部件3需要调整为事件C,
由题意可知,P(A)=0.1,P(B)=0.2,P(C)=0.3.
部件1,2中至少有1个需要调整的概率为
1-[1-P(A)][1-P(B)]=1-0.9×0.8=1-0.72=0.28.
(2)由题意可知X的取值为0,1,2,3.
P(X=0)=[1-P(A)][1-P(B)][1-P(C)]=(1-0.1)×(1-0.2)×(1-0.3)=0.504,P(X=1)=P(A)[1-P(B)][1-P(C)]+[1-P(A)]P(B)[1-P(C)]+[1-P(A)][1-P(B)]P(C)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398,P(X=2)=P(A)P(B)[1-P(C)]+P(A)[1-P(B)]P(C)+[1-P(A)]P(B)P(C)
=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092,
P(X=3)=P(A)P(B)P(C)=0.1×0.2×0.3=0.006,
故X的分布列为
X 0 1 2 3
P 0.504 0.398 0.092 0.006
所以E(X)=0.504×0+0.398×1+0.092×2+0.006×3=0.6,
D(X)=(0-0.6)2×0.504+(1-0.6)2×0.398+(2-0.6)2×0.092+(3-0.6)2×0.006=0.46.
链接·2025高考试题
(2025·全国一卷)有5个相同的球,分别标有数字1,2,3,4,5,从中有放回地随机取3次,每次取1个球.记X为这5个球中至少被取出1次的球的个数,则X的数学期望E(X)=________.
所以E(X)=1×+2×+3×=.]
X 1 2 3
P
[X的所有可能取值为1,2,3,则P(X=1)===,P(X=2)=×6==,P(X=3)=×6==,所以X的分布列为
反思领悟 本例求均值与方差的关键是确定随机变量的所有可能取值,写出分布列,正确运用均值、方差公式进行计算.
巩固迁移4 甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10 分,负方得0 分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.用X表示乙学校的总得分,求X 的分布列与期望.
[解] 依题可知, X 的可能取值为0,10,20,30,
P(X=0)=0.5×0.4×0.8=0.16,
P(X=10)=0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.44,
P(X=20)=0.5×0.6×0.8+0.5×0.4×0.2+0.5×0.6×0.2=0.34,
P(X=30)=0.5×0.6×0.2=0.06.
所以X的分布列为
X 0 10 20 30
P 0.16 0.44 0.34 0.06
E(X)=0×0.16+10×0.44+20×0.34+30×0.06=13.
考点三 均值与方差在决策中的应用
[典例5] (经典题)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
[解] (1)由已知可得,X的所有可能取值为0,20,100,
P(X=0)=1-0.8=0.2,
P(X=20)=0.8×(1-0.6)=0.32,
P(X=100)=0.8×0.6=0.48,
所以X的分布列为
X 0 20 100
P 0.2 0.32 0.48
(2)由(1)可知当小明先回答A类问题时,E(X)=0×0.2+20×0.32+100×0.48=54.4.
当小明先回答B类问题时,记Y为小明的累计得分,
则Y的所有可能取值为0,80,100,
P(Y=0)=1-0.6=0.4,
P(Y=80)=0.6×(1-0.8)=0.12,
P(Y=100)=0.6×0.8=0.48,
所以Y的分布列为
Y 0 80 100
P 0.4 0.12 0.48
则E(Y)=0×0.4+80×0.12+100×0.48=57.6.
因为57.6>54.4,即E(Y)>E(X),
所以为使累计得分的期望最大,小明应选择先回答B类问题.
反思领悟 随机变量的均值和方差从整体和全局上刻画了随机变量,是生产实际中用于方案取舍的重要理论依据.一般先比较均值,若均值相同,再用方差来决定.
巩固迁移5 有甲、乙两个建材厂,都想投标参加某重点建设项目,为了对重点建设项目负责,政府到两建材厂抽样检查,他们从中各取等量的样本检查它们的抗拉强度指数如表:
X 110 120 125 130 135
P 0.1 0.2 0.4 0.1 0.2
Y 100 115 125 130 145
P 0.1 0.2 0.4 0.1 0.2
其中X和Y分别表示甲、乙两厂材料的抗拉强度,比较甲、乙两厂材料哪一种稳定性好.
[解] E(X)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125,
E(Y)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125,
D(X)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50,
D(Y)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165,
由于E(X)=E(Y),D(X)
[典例] 有编号为1,2,3,4的4个学生,入座编号为1,2,3,4的4个座位,规定每个学生坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为X.求随机变量X的分布列.
[解] 因为学生所坐的座位号与该生的编号不同的学生人数为X,
由题意可知X的可能取值是0,2,3,4,
所以P(X=0)==,P(X=2)==,
P(X=3)==,P(X=4)=1-=,
所以随机变量X的分布列为
X 0 2 3 4
P
反思领悟 求离散型随机变量分布列的关键是求随机变量所取值对应的概率.
应用体验 甲同学参加化学竞赛初赛,考试分为笔试、口试、实验三个项目,各单项通过考试的概率依次为.记甲同学三个项目中通过考试的个数为X,求随机变量X的分布列.
[解] 随机变量X的所有可能取值为0,1,2,3.
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==.
所以随机变量X的分布列为
X 0 1 2 3
P
随堂练习
1.(人教A版选择性必修第三册P71习题7.3T3改编)随机变量X的分布列为P(X=0)=0.2,P(X=1)=a,P(X=2)=b,若E(X)=1,则a=________;b=________.
0.6 0.2 [由题意知,
解得]
0.6
0.2
2.(人教A版选择性必修第三册P66练习T1改编)已知随机变量X的分布列为
X 1 2 3 4 5
P 0.1 0.3 0.4 0.1 0.1
则E(X)=________;E(3X+2)=________.
2.8 10.4 [E(X)=1×0.1+2×0.3+3×0.4+4×0.1+5×0.1=2.8,E(3X+2)=3E(X)+2=3×2.8+2=10.4.]
10.4
2.8
3.医学上发现,某种病毒侵入人体后,人的体温会升高.记病毒侵入后人体的平均体温为X ℃.医学统计发现,X的分布列如表所示.
X 37 38 39 40
P 0.1 0.5 0.3 0.1
(1)求出E(X),D(X);
(2)已知人体体温为X ℃时,相当于Y=1.8X+32(℃),求E(Y),D(Y).
[解] (1)由题可得E(X)=37×0.1+38×0.5+39×0.3+40×0.1=38.4,D(X)=(37-38.4)2×0.1+(38-38.4)2×0.5+(39-38.4)2×0.3+(40-38.4)2×0.1=0.64,
(2)由Y=1.8X+32可知,E(Y)=1.8E(X)+32=1.8×38.4+32=101.12,D(Y)=1.82×D(X)=×0.64=2.073 6.
【教用·备选题】
1.(2024·马鞍山期末)随机变量X的分布列如表所示,则D(bX)的最大值为( )
√
X 1 2 3
P a 2b a
A. B.
C. D.
D [由题可知2a+2b=1,即a+b=,
E(X)=a+4b+3a=4(a+b)=2,D(X)=a(1-2)2+(3-2)2a=2a,
则D(bX)=b2D(X)=2ab2=-2b3+b2,
令f (b)=-2b3+b2,则f ′(b)=-6b2+2b=-2b(3b-1),
则f (b)在上单调递增,在上单调递减,
所以f (b)max=f =,则D(bX)的最大值为.
故选D.]
2.(2024·泸州江阳区期末)已知随机变量X的概率分布列为P(X=n)=(n=1,2,3,…,10),则实数a=________.
[随机变量X的概率分布列为P(X=n)=(n=1,2,3,…,10),∴
=1,
∴a=a=1,则实数a=.]
3.(2025·上海普陀模拟)一个盒子里有1个红球和2个绿球,每次拿一个,不放回,拿出红球即停,设拿出绿球的个数为X,则E(X)=__________.
1 [由题意,随机变量X的所有可能取值为0,1,2,
则P(X=0)=;P(X=1)==;P(X=2)==,
所以E(X)=0×+1×+2×=1.]
1
4.(2024·四川雅安高三联考)为了促进消费,某商场针对会员客户推出会员积分兑换商品活动:每位会员客户可在价值80元、90元、100元的A,B,C三种商品中选择一种使用积分进行兑换,每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1 000积分,且甲
兑换A,B,C三种商品的概率分别为,乙兑换A,B,C三种商品的概率分别为,且他们兑换何种商品相互独立.
(1)求甲、乙两人兑换同一种商品的概率;
(2)记X为两人兑换商品后的积分总余额,求X的分布列与期望.
[解] (1)由题可知,甲、乙两人兑换同一种商品的概率为=.
(2)由题意,兑换A,B,C三种商品所需的积分分别为800,900,
1 000,则X的取值可能为0,100,200,300,400,
P(X=0)==,P(X=100)==,
P(X=200)==,
P(X=300)==,
P(X=400)==,
则X的分布列为
X 0 100 200 300 400
P
E(X)=0×+100×+200×+300×+400×=250.
课后习题(六十五) 离散型随机变量及其分布列、数字特征
1.(北师大版选择性必修第一册P202习题6-2A组T3改编)某射击运动员射击所得的环数X的分布列如下表:
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
X 5 6 7 8 9 10
P 0.06 0.06 0.09 a 0.29 0.22
此运动员“射击一次命中的环数大于6且小于9”的概率为( )
A.0.43 B.0.37 C.0.51 D.0.79
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [由分布列的性质知a=1-(0.06+0.06+0.09+0.29+0.22)=0.28.
∴P(6
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(多选)(人教A版选择性必修第三册P70练习T1改编)设离散型随机变量X的分布列为
X 0 1 2 3 4
P q 0.4 0.1 0.2 0.2
若离散型随机变量Y满足Y=2X+1,则下列结果正确的有( )
A.q=0.1 B.E(X)=2,D(X)=1.4
C.E(X)=2,D(X)=1.8 D.E(Y)=5,D(Y)=7.2
√
√
ACD [由离散型随机变量X的分布列的性质得:
q=1-0.4-0.1-0.2-0.2=0.1,
E(X)=0×0.1+1×0.4+2×0.1+3×0.2+4×0.2=2,
D(X)=(0-2)2×0.1+(1-2)2×0.4+(2-2)2×0.1+(3-2)2×0.2+(4-2)2×0.2=1.8,
∵离散型随机变量Y满足Y=2X+1,
∴E(Y)=2E(X)+1=5,D(Y)=4D(X)=7.2.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(多选)(苏教版选择性必修第二册P115练习T2改编)设随机变量ξ的
分布列为P=ak(k=1,2,3,4,5),则( )
A.a= B.P=
C.P= D.P(ξ=1)=
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
AB [对于选项A,∵随机变量ξ的分布列为P=ak(k=1,2,3,4,5),∴P+P+P+P+P(ξ=1)=a+2a+3a+4a+5a=1,解得a=,故A正确;对于选项B,=P=3×=,故B正确;对于选项C,P=P+P=+2×=,故C错误;对于选项D,P(ξ=1)=5×=,故D错误.故选AB.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教A版选择性必修第三册P68方差公式简化计算改编)已知离散型随机变量X的取值为有限个,E(X)=,D(X)=,则E(X2)=________.
[因为E(X)=,D(X)=,由D(X)=E(X 2)-(E(X))2,
得E(X 2)=D(X)+(E(X))2==.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·重庆长寿区期末)设随机变量X的概率分布列为
√
X 1 2 3 4
P m
则P(|X-3|=1)=( )
A. B. C.D.
题号
1
3
5
2
4
6
8
7
9
10
11
12
B [由题意得+m+=1,解得m=,
随机变量X的概率分布列为
X 1 2 3 4
P
∴P(|X-3|=1)=P(X=2)+P(X=4)=,故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2024·眉山仁寿县期末)已知随机变量X的分布列为
X 0 1 2
P m
若Y=3X-2,则E(Y)=( )
A. B.
C.- D.-
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
A [由题可知+m=1,解得m=,
则E(X)=0×+1×+2×=,
所以E(Y)=3E(X)-2=3×-2=.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2025·湖北咸宁模拟)设0
X 0 a 1
P
则当a在(0,1)内减小时( )
A.D(X)减小 B.D(X)增大
C.D(X)先减小后增大 D.D(X)先增大后减小
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [根据题意可得,E(X)==,
D(X)===,
所以D(X)在上单调递减,在上单调递增,所以D(X)先减小后增大.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(多选)(2024·四川攀枝花月考)已知正数a,b,c成等差数列,且随机变量X的分布列为
√
X 1 2 3
P a b c
下列选项正确的是( )
A.b= B.a+c=
C.
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
BCD [正数a,b,c成等差数列,则a+c=2b,
又由分布列的性质可知,a+b+c=1,
解得故A错误,B正确;
由a+c=,得0
D(X)=a++c=++c=-4c2+c+=
-4+,
当c=时,D(X)取得最大值,且最大值为,D正确.
故选BCD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2024·重庆沙坪坝区月考)已知随机变量ξ,D(10ξ)=,则ξ的标准差为________.
[∵D(10ξ)=100D(ξ)=,∴D(ξ)=,
∴ξ的标准差==.
∴ξ的标准差为.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2025·保定模拟)已知随机变量X的所有可能取值为1,2,3,其分布列为
X 1 2 3
P P1 P2 P3
若E(X)=,则P3-P1=________.
-
题号
1
3
5
2
4
6
8
7
9
10
11
12
- [因为E(X)=P1+2P2+3P3=,①
且P1+P2+P3=1,②
所以①-②×2可得,P1+2P2+3P3-2(P1+P2+P3)=P3-P1=-.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2024·广州开学考试节选)某公司拟通过摸球中奖的方式对员工发放节日红包.在一个不透明的袋子中装有n个形状大小相同的标有面值的球,每位员工从球袋中一次性随机摸取m个球(m≤n),摸完后全部放回袋中,球上所标的面值之和为该员工所获得的红包数额.
若n=5,m=4,当袋中的球中有1个所标面值为10元,2个为20元,1个为30元,1个为40元时,求员工所获得红包数额的数学期望与方差.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 设X为员工获得的红包数额,则X可能取值为80,90,100,110,
所以P(X=80)==,P(X=90)==,
P(X=100)==,P(X=110)==,
所以E(X)=80×+90×+100×+110×=96,
D(X)=(80-96)2×+(90-96)2×+(100-96)2×+(110-96)2×=
104.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2024·山东潍坊高三模拟)某投资公司对以下两个项目进行前期市场调研.项目A:通信设备.根据调研,投资到该项目上,所有可能结果为获利40%,损失20%,不赔不赚,且这三种情况发生的概率分别为,a.项目B:新能源汽车.根据调研,投资到该项目上,所有可能结果为获利30%,亏损10%,且这两种情况发生的概率分别为b,c.经测算,当投入A,B两个项目的资金相等时,它们所获利润的均值也相等.
(1)求a,b,c的值;
(2)若将100万元全部投到其中的一个项目,请你从投资回报稳定性的角度考虑,为投资公司选择一个合适的项目.
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)依题意,得+a=1, 所以a=.
设投入项目A,B的资金都为x万元,随机变量X1和X2分别表示投资项目A和B所获的利润,则X1和X2的分布列分别为
X1 0.4x -0.2x 0
P
X2 0.3x -0.1x
P b c
由分布列得E(X1)=0.4x×+(-0.2x)×+0×=0.2x,
E(X2)=0.3bx-0.1cx.
因为E(X1)=E(X2),所以0.3bx-0.1cx=0.2x,
即0.3b-0.1c=0.2.
又b+c=1,解得b=,c=.
所以a=,b=,c=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)当投入100万元资金时,
由(1)知x=100,
所以E(X1)=E(X2)=20,
D(X1)=(40-20)2×+(-20-20)2×+(0-20)2×=600,
D(X2)=(30-20)2×+(-10-20)2×=300.
所以D(X1)>D(X2),这说明虽然项目A和项目B的平均收益相等,但项目B更稳妥,所以从投资回报稳定性的角度考虑,建议该投资公司选择项目B.
题号
1
3
5
2
4
6
8
7
9
10
11
12
谢 谢 !
同课章节目录
