《高考快车道》2026版高三一轮总复习数学(基础版)107 第九章 思维进阶14 概率模型的辨识与应用 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)107 第九章 思维进阶14 概率模型的辨识与应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-12-04 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
第九章 计数原理、概率、随机变量及其分布
思维进阶14 概率模型的辨识与应用
高考常考的概率模型有相互独立事件的概率模型、二项分布模型、超几何分布模型和正态分布模型,其中二项分布与超几何分布模型的辨识一直是学生的难点和易错点.
二项分布与超几何分布的区别与联系
超几何分布 二项分布
区别 描述的是不放回抽样问题(总体在变化),一次性取 描述的是有放回抽样问题(总体不改变),一个一个地取
超几何分布 二项分布
区别 考察对象分为两类 每一次试验是伯努利试验
已知各类对象的个数
联系 (当总体容量很大时)超几何分布可近似看作二项分布
下面就高考常考的四种概率模型予以辨识说明.
题型一 相互独立事件概率模型
[典例1] (2024·扶风市期末)某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13 s内(称为合格)的概率分别为,若对这三名短跑运动员的100米跑的成绩进行一次检验,求:
(1)三人都合格的概率;
(2)三人都不合格的概率;
(3)三人中恰有两人合格的概率.
[解] (1)设甲、乙、丙三人100米跑成绩合格分别为事件A,B,C,显然事件A,B,C相互独立,且P(A)=,P(B)=,P(C)=,设恰有k人合格的概率为Pk(k=0,1,2,3),则三人都合格的概率:P3=P(ABC)=P(A)P(B)P(C)==.
(2)三人都不合格的概率:P0=P()·P()==.
(3)三人中恰有两人合格的概率:P2=P(ABBC)==.
反思领悟 相互独立事件概率模型的特征
(1)实际问题中所涉及的若干事件中每一个是否发生互不影响;
(2)因为事件A1,A2,A3,…,An相互独立,则满足·A2·A3·…·An)=;
(3)求解相互独立事件的概率问题时,常涉及互斥、对立事件的概率求值.
题型二 二项分布概率模型
[典例2] 甲、乙两名运动员进行羽毛球单打比赛,根据以往比赛的胜负情况知道.每一局甲胜的概率为,乙胜的概率为.比赛采用三局两胜制,先胜两局者获胜.商定每局比赛(决胜局第三局除外)胜者得3分,败者得1分;决胜局胜者得2分,败者得0分.已知各局比赛相互独立.
(1)求比赛结束甲得6分的概率;
(2)设比赛结束乙得X分,求随机变量X的分布列与数学期望.
[解] (1)记事件A为“比赛结束甲得6分”,
则事件A为“乙以0∶2败给甲或乙以1∶2败给甲”,
所以P(A)===.
所以比赛结束甲得6分的概率为.
(2)由题意得,X可取2,4,6,
则P(X=2)==,P(X=4)==,
P(X=6)==,
即X的分布列为
X 2 4 6
P
所以E(X)=2×+4×+6×=.
反思领悟 二项分布概率模型的特征
(1)在每一次试验中,试验结果只有两个,即发生与不发生;
(2)各次试验中的事件是相互独立的;
(3)在每一次试验中,事件发生的概率保持不变.
题型三 超几何分布概率模型
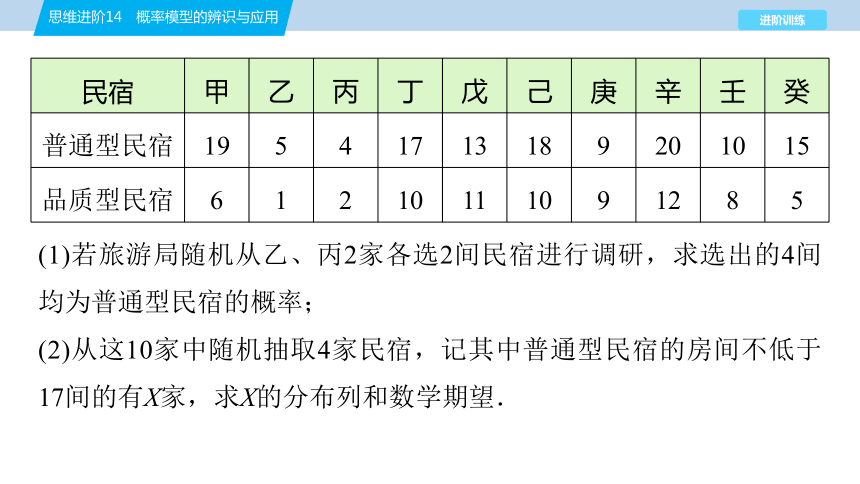
[典例3] (2024·河南安阳高三期末)不负青山,力换“金山”,民宿旅游逐渐成为一种热潮,山野乡村的民宿深受广大旅游爱好者的喜爱.某地区结合当地资源,按照“山上生态做减法、山下产业做加法”的思路,科学有序地发展环山文旅康养产业,温泉度假小镇、环山绿道、农家乐提档升级、特色民宿群等一批生态产业项目加快实施.为了在节假日接待好游客,该地旅游局对本地区各乡村的普通型民宿和品质型民宿进行了调研,随机抽取了10家乡村民宿,统计得到各家的房间数如下表:
(1)若旅游局随机从乙、丙2家各选2间民宿进行调研,求选出的4间均为普通型民宿的概率;
(2)从这10家中随机抽取4家民宿,记其中普通型民宿的房间不低于17间的有X家,求X的分布列和数学期望.
民宿 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
普通型民宿 19 5 4 17 13 18 9 20 10 15
品质型民宿 6 1 2 10 11 10 9 12 8 5
[解] (1)设“从乙家选2间民宿,选到的2间民宿为普通型”为事件A;“从丙家选2间民宿,选到的2间民宿为普通型”为事件B,
所以选出的4间均为普通型民宿的概率为P(AB)=P(A)P(B)==.
(2)这10家民宿,其中普通型民宿的房间不低于17间的有4家,随机
变量X的可能取值有0,1,2,3,4,则P(X=0)===,
P(X=1)===,P(X=2)===,
P(X=3)===,P(X=4)==,
即X的分布列为
X 0 1 2 3 4
P
所以E(X)=0×+1×+2×+3×+4×==1.6.
反思领悟 解决超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)超几何分布中,只要知道M,N,n就可以利用公式求出X取不同k的概率P(X=k),从而求出X的分布列,利用均值、方差的定义求出随机变量的均值和方差.
题型四 二项分布与超几何分布的区别
[典例4] 某食品厂为了检查一条自动包装流水线的生产情况,对该流水线上的产品进行简单随机抽样,获得数据如下表:
分组区间 (单位:克) [490, 495) [495, 500) [500, 505) [505, 510) [510,
515]
产品件数 3 4 7 5 1
包装质量在[495,510)克的产品为一等品,其余为二等品.
(1)估计从该流水线任取一件产品为一等品的概率;
(2)从上述抽取的样本产品中任取2件,设X为一等品的产品数量,求X的分布列;
(3)从该流水线上任取2件产品,设Y为一等品的产品数量,求Y的分布列;试比较期望E(X)与期望E(Y)的大小.(结论不要求证明)
[解] (1)样本中一共有3+4+7+5+1=20(件)产品,包装质量在[495,510)克的产品有4+7+5=16(件),故从该流水线任取一件产
品为一等品的概率P==.
(2)依题意X的可能取值为0,1,2,
P(X=2)==,P(X=1)==,P(X=0)==,
故X的分布列为
X 0 1 2
P
(3)由(2)可得E(X)=2×+1×+0×=.
依题意Y~B,则Y的可能取值为0,1,2,
P(Y=2)==,P(X=1)==,
P(X=0)==,
故Y的分布列为
Y 0 1 2
P
所以E(Y)=2×=.
所以E(Y)=E(X).
反思领悟 1.n次试验中,某一事件A出现的次数X可能服从超几何分布或二项分布.当这n次试验是独立重复试验时,X服从二项分布;当这n次试验是不放回摸球模型问题时,事件A为摸到某种特性(如某种颜色)的球时,X服从超几何分布.
2.在不放回n次摸球试验中,摸到某种颜色球的次数X服从超几何分布,但是当袋子中的球的数目N很大时,X的分布列近似于二项分布,并且随着N的增加,这种近似的精度也增加.
从以上分析可以看出两者之间的联系:
当调查研究的样本容量非常大时,在有放回地抽取与无放回地抽取条件下,计算得到的概率非常接近,可以近似把超几何分布认为是二项分布.
超几何分布与二项分布是有联系的,看它们的期望公式:
(1)在含有M件次品的N件产品中,任取n件,其中恰有X件次品,随机变量X服从超几何分布,超几何分布的期望计算公式为E(X)=.
(2)随机变量X服从二项分布,记作X~B(n,p),E(X)=np.
当超几何分布中的N→+∞时,→p,此时可以把超几何分布中的不放回抽样问题,近似看作是有放回抽样问题,再次说明N→+∞时,可以把超几何分布看作二项分布.
题型五 正态分布模型
[典例5] (2024·益阳安化县期末)随着网络技术的迅速发展,各种购物群成为网络销售的新渠道.2024年11月某地脐橙开始采摘上市,一脐橙基地随机抽查了100个购物群的销售情况,各购物群销售脐橙的情况如下:
脐橙数 量/盒 [100, 200) [200, 300) [300, 400) [400, 500) [500,
600]
购物群 数量/个 12 18 m 32 18
(1)求实数m的值,并用组中值(每组的中点值)估计这100个购物群销售脐橙总量的平均数;
(2)假设所有购物群销售脐橙的数量X~N(μ,σ2),其中μ为(1)中的平均数,σ2=14 400.若该脐橙基地参与销售的购物群约有1 000个,销售的脐橙在[256,616](单位:盒)内的群为“A级群”,销售数量小于256盒的购物群为“B级群”,销售数量大于616盒的购物群为“特级群”,该脐橙基地对每个“特级群”奖励600元,每个“A级群”奖励100元,对“B级群”不奖励,则该脐橙基地大约需要准备多少奖金?(群的个数按四舍五入取整数)
附:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
[解] (1)由题意得,12+18+m+32+18=100,解得m=20,
则这100个购物群销售脐橙总量的平均数为:(150×12+250×18+
350×20+450×32+550×18)=376.
(2)由题意,μ=376,σ=120,则256=μ-σ,616=μ+2σ,
故P(256≤X≤616)=P(μ-σ≤X≤μ+2σ)=×P(μ-σ≤X≤μ+σ)+×P(μ-2σ≤X≤μ+2σ)≈×0.682 7+×0.954 5=0.818 6,
故“A级群”约有1 000×0.818 6=818.6≈819(个),
P(X>616)=P(X>μ+2σ)=[1-P(μ-2σ≤X≤μ+2σ)]≈(1-0.954 5)≈0.023,
故“特级群”约有1 000×0.023=23(个),
则依题意,需要资金为819×100+23×600=95 700(元),即该脐橙基地大约需要准备95 700元.
反思领悟 解答正态分布的实际应用题,其关键是利用图象的对称性,由μ,σ把分布区间转化为3σ特殊区间,从而求出概率.在此过程中用到转化和数形结合思想.
进阶训练(十四) 概率模型的辨识与应用
1.已知某公司生产的风干牛肉干是按包销售的,每包牛肉干的质量M(单位:g)服从正态分布N(250,σ2),且P(M<248)=0.1.
(1)若从公司销售的牛肉干中随机选取3包,求这3包中恰有2包质量不小于248 g的概率;
(2)若从公司销售的牛肉干中随机选取K(K为正整数)包,记质量在248 g~252 g的包数为X,且D(X)>320,求K的最小值.
题号
1
3
5
2
4
[解] (1)因为P(M<248)=0.1,所以P(M≥248)=1-0.1=0.9,
则这3包中恰有2包质量不小于248 g的概率为×0.92×0.1=0.243.
(2)因为P(M<248)=0.1,所以P(248<M<252)=(0.5-0.1)×2=0.8.
依题意可得 X~B(K,0.8),
所以D(X)=K×0.8×(1-0.8)=0.16K,
因为D(X)>320,所以K>2 000,
又K为正整数,所以K的最小值为2 001.
题号
1
3
5
2
4
2.(2024·眉山市东坡区期末)眉山市位于四川西南,有“千载诗书城,人文第一州”的美誉,这里是大文豪苏轼、苏洵、苏辙的故乡,也是人们旅游的好地方.在今年的国庆黄金周,为了丰富游客的文化生活,每天在东坡故里三苏祠举行“三苏文化”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为,乙队中3人答对的概率分别为,且各人回答正确与否相互之间没有影响.
(1)分别求甲队总得分为0分,2分的概率;
(2)求甲队得2分,乙队得1分的概率.
题号
1
3
5
2
4
[解] (1)记“甲队总得分为0分”为事件A,“甲队总得分为2分”为事件B,
甲队总得分为0分,即甲队三人都回答错误,
其概率P(A)==.
甲队总得分为2分,即甲队三人中有1人答错,其余两人答对,
其概率P(B)==.
题号
1
3
5
2
4
(2)记“乙队得1分”为事件C,“甲队得2分,乙队得1分”为事件D,
事件C即乙队三人中有2人答错,其余1人答对,
则P(C)==,
甲队得2分,乙队得1分即事件B,C同时发生,
则P(D)=P(B)P(C)==.
题号
1
3
5
2
4
3.(2025·广西玉林统考模拟)某地区期末进行了统一考试,为做好本次考试的评价工作,现从中随机抽取了50名学生的成绩,经统计,这批学生的成绩全部介于40至100之间,将数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,制成了如图所示的频率分布直方图.
题号
1
3
5
2
4
(1)求频率分布直方图中m的值;在这50名学生中用分层随机抽样的方法从成绩在[70,80),[80,90),[90,100]的三组中抽取了11人,再从这11人中随机抽取3人,记X为3人中成绩在[80,90)的人数,求P(X=1);
(2)规定成绩在的为A等级,成绩在[70,90)的为B等级,其他为C等级.以样本估计总体,用频率代替概率.从所有参加考试的同学中随机抽取3人,求获得B等级的人数不少于2的概率.
题号
1
3
5
2
4
[解] (1)∵(0.004+0.022+0.030+0.028+m+0.004)×10=1,
∴m=0.012.
∵成绩在[70,80),[80,90),的频率之比为0.28∶0.12∶0.04=7∶3∶1,
∴抽取的11人中,成绩在[80,90)的人数为11×=3,
∴P(X=1)==.
题号
1
3
5
2
4
(2)用频率估计概率,获得B等级的概率为(0.028+0.012)×10=0.4=,
记抽取的3人中,获得B等级的人数为Y,则Y~,
∴P(Y≥2)=P(Y=2)+P(Y=3)==,即获得B等级的人数不少于2的概率为.
题号
1
3
5
2
4
4.为庆祝建军节的到来,某校举行“强国强军”知识竞赛.该校某班经过层层筛选,还有最后一个参赛名额要在A,B两名学生中产生,该班委设计了一个选拔方案:A,B两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生A能正确回答其中的4个问题,而学生B能正确回答每个问题的概率均为.A,B两名学生对每个问题回答正确与否都是相互独立的.
(1)分别求A,B两名学生恰好答对2个问题的概率;
(2)设A答对的题数为X,B答对的题数为Y,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
题号
1
3
5
2
4
[解] (1)由题意,知A恰好答对2个问题的概率为P1==,
B恰好答对2个问题的概率为
P2==.
题号
1
3
5
2
4
(2)X的可能取值为1,2,3,则P(X=1)==,P(X=2)==,P(X=3)==,所以E(X)=1×+2×+3×=2,
D(X)=(1-2)2×+(2-2)2×+(3-2)2×=.
易知Y~B,所以E(Y)=3×=2,D(Y)=3×=.
因为E(X)=E(Y),D(X)题号
1
3
5
2
4
5.某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的质量(单位:克),质量的分组区间为[490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图(如图).
(1)根据频率分布直方图,求质量超过505克的产
品数量;
(2)在上述抽取的40件产品中任取2件,设X为质
量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取2件产品,设Y为质量超过
505克的产品数量,求Y的分布列.
题号
1
3
5
2
4
[解] (1)质量超过505克的产品的频率为5×0.05+5×0.01=0.3,
所以质量超过505克的产品数量为40×0.3=12.
(2)质量超过505克的产品数量为12,则质量未超过505克的产品数量为28,X的取值为0,1,2,X服从超几何分布.
P(X=0)==,P(X=1)==,
P(X=2)==,
所以X的分布列为
X 0 1 2
P
题号
1
3
5
2
4
(3)根据样本估计总体的思想,取一件产品,该产品的质量超过505克的概率为=.
从流水线上任取2件产品互不影响,该问题可看成2重伯努利试
验,质量超过505克的件数Y的可能取值为0,1,2,且Y~B,P(Y=k)=,k=0,1,2.
题号
1
3
5
2
4
题号
1
3
5
2
4
所以P(Y=0)==,
P(Y=1)==,
P(Y=2)==.
所以Y的分布列为
Y 0 1 2
P
谢 谢 !
第九章 计数原理、概率、随机变量及其分布
思维进阶14 概率模型的辨识与应用
高考常考的概率模型有相互独立事件的概率模型、二项分布模型、超几何分布模型和正态分布模型,其中二项分布与超几何分布模型的辨识一直是学生的难点和易错点.
二项分布与超几何分布的区别与联系
超几何分布 二项分布
区别 描述的是不放回抽样问题(总体在变化),一次性取 描述的是有放回抽样问题(总体不改变),一个一个地取
超几何分布 二项分布
区别 考察对象分为两类 每一次试验是伯努利试验
已知各类对象的个数
联系 (当总体容量很大时)超几何分布可近似看作二项分布
下面就高考常考的四种概率模型予以辨识说明.
题型一 相互独立事件概率模型
[典例1] (2024·扶风市期末)某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13 s内(称为合格)的概率分别为,若对这三名短跑运动员的100米跑的成绩进行一次检验,求:
(1)三人都合格的概率;
(2)三人都不合格的概率;
(3)三人中恰有两人合格的概率.
[解] (1)设甲、乙、丙三人100米跑成绩合格分别为事件A,B,C,显然事件A,B,C相互独立,且P(A)=,P(B)=,P(C)=,设恰有k人合格的概率为Pk(k=0,1,2,3),则三人都合格的概率:P3=P(ABC)=P(A)P(B)P(C)==.
(2)三人都不合格的概率:P0=P()·P()==.
(3)三人中恰有两人合格的概率:P2=P(ABBC)==.
反思领悟 相互独立事件概率模型的特征
(1)实际问题中所涉及的若干事件中每一个是否发生互不影响;
(2)因为事件A1,A2,A3,…,An相互独立,则满足·A2·A3·…·An)=;
(3)求解相互独立事件的概率问题时,常涉及互斥、对立事件的概率求值.
题型二 二项分布概率模型
[典例2] 甲、乙两名运动员进行羽毛球单打比赛,根据以往比赛的胜负情况知道.每一局甲胜的概率为,乙胜的概率为.比赛采用三局两胜制,先胜两局者获胜.商定每局比赛(决胜局第三局除外)胜者得3分,败者得1分;决胜局胜者得2分,败者得0分.已知各局比赛相互独立.
(1)求比赛结束甲得6分的概率;
(2)设比赛结束乙得X分,求随机变量X的分布列与数学期望.
[解] (1)记事件A为“比赛结束甲得6分”,
则事件A为“乙以0∶2败给甲或乙以1∶2败给甲”,
所以P(A)===.
所以比赛结束甲得6分的概率为.
(2)由题意得,X可取2,4,6,
则P(X=2)==,P(X=4)==,
P(X=6)==,
即X的分布列为
X 2 4 6
P
所以E(X)=2×+4×+6×=.
反思领悟 二项分布概率模型的特征
(1)在每一次试验中,试验结果只有两个,即发生与不发生;
(2)各次试验中的事件是相互独立的;
(3)在每一次试验中,事件发生的概率保持不变.
题型三 超几何分布概率模型
[典例3] (2024·河南安阳高三期末)不负青山,力换“金山”,民宿旅游逐渐成为一种热潮,山野乡村的民宿深受广大旅游爱好者的喜爱.某地区结合当地资源,按照“山上生态做减法、山下产业做加法”的思路,科学有序地发展环山文旅康养产业,温泉度假小镇、环山绿道、农家乐提档升级、特色民宿群等一批生态产业项目加快实施.为了在节假日接待好游客,该地旅游局对本地区各乡村的普通型民宿和品质型民宿进行了调研,随机抽取了10家乡村民宿,统计得到各家的房间数如下表:
(1)若旅游局随机从乙、丙2家各选2间民宿进行调研,求选出的4间均为普通型民宿的概率;
(2)从这10家中随机抽取4家民宿,记其中普通型民宿的房间不低于17间的有X家,求X的分布列和数学期望.
民宿 甲 乙 丙 丁 戊 己 庚 辛 壬 癸
普通型民宿 19 5 4 17 13 18 9 20 10 15
品质型民宿 6 1 2 10 11 10 9 12 8 5
[解] (1)设“从乙家选2间民宿,选到的2间民宿为普通型”为事件A;“从丙家选2间民宿,选到的2间民宿为普通型”为事件B,
所以选出的4间均为普通型民宿的概率为P(AB)=P(A)P(B)==.
(2)这10家民宿,其中普通型民宿的房间不低于17间的有4家,随机
变量X的可能取值有0,1,2,3,4,则P(X=0)===,
P(X=1)===,P(X=2)===,
P(X=3)===,P(X=4)==,
即X的分布列为
X 0 1 2 3 4
P
所以E(X)=0×+1×+2×+3×+4×==1.6.
反思领悟 解决超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)超几何分布中,只要知道M,N,n就可以利用公式求出X取不同k的概率P(X=k),从而求出X的分布列,利用均值、方差的定义求出随机变量的均值和方差.
题型四 二项分布与超几何分布的区别
[典例4] 某食品厂为了检查一条自动包装流水线的生产情况,对该流水线上的产品进行简单随机抽样,获得数据如下表:
分组区间 (单位:克) [490, 495) [495, 500) [500, 505) [505, 510) [510,
515]
产品件数 3 4 7 5 1
包装质量在[495,510)克的产品为一等品,其余为二等品.
(1)估计从该流水线任取一件产品为一等品的概率;
(2)从上述抽取的样本产品中任取2件,设X为一等品的产品数量,求X的分布列;
(3)从该流水线上任取2件产品,设Y为一等品的产品数量,求Y的分布列;试比较期望E(X)与期望E(Y)的大小.(结论不要求证明)
[解] (1)样本中一共有3+4+7+5+1=20(件)产品,包装质量在[495,510)克的产品有4+7+5=16(件),故从该流水线任取一件产
品为一等品的概率P==.
(2)依题意X的可能取值为0,1,2,
P(X=2)==,P(X=1)==,P(X=0)==,
故X的分布列为
X 0 1 2
P
(3)由(2)可得E(X)=2×+1×+0×=.
依题意Y~B,则Y的可能取值为0,1,2,
P(Y=2)==,P(X=1)==,
P(X=0)==,
故Y的分布列为
Y 0 1 2
P
所以E(Y)=2×=.
所以E(Y)=E(X).
反思领悟 1.n次试验中,某一事件A出现的次数X可能服从超几何分布或二项分布.当这n次试验是独立重复试验时,X服从二项分布;当这n次试验是不放回摸球模型问题时,事件A为摸到某种特性(如某种颜色)的球时,X服从超几何分布.
2.在不放回n次摸球试验中,摸到某种颜色球的次数X服从超几何分布,但是当袋子中的球的数目N很大时,X的分布列近似于二项分布,并且随着N的增加,这种近似的精度也增加.
从以上分析可以看出两者之间的联系:
当调查研究的样本容量非常大时,在有放回地抽取与无放回地抽取条件下,计算得到的概率非常接近,可以近似把超几何分布认为是二项分布.
超几何分布与二项分布是有联系的,看它们的期望公式:
(1)在含有M件次品的N件产品中,任取n件,其中恰有X件次品,随机变量X服从超几何分布,超几何分布的期望计算公式为E(X)=.
(2)随机变量X服从二项分布,记作X~B(n,p),E(X)=np.
当超几何分布中的N→+∞时,→p,此时可以把超几何分布中的不放回抽样问题,近似看作是有放回抽样问题,再次说明N→+∞时,可以把超几何分布看作二项分布.
题型五 正态分布模型
[典例5] (2024·益阳安化县期末)随着网络技术的迅速发展,各种购物群成为网络销售的新渠道.2024年11月某地脐橙开始采摘上市,一脐橙基地随机抽查了100个购物群的销售情况,各购物群销售脐橙的情况如下:
脐橙数 量/盒 [100, 200) [200, 300) [300, 400) [400, 500) [500,
600]
购物群 数量/个 12 18 m 32 18
(1)求实数m的值,并用组中值(每组的中点值)估计这100个购物群销售脐橙总量的平均数;
(2)假设所有购物群销售脐橙的数量X~N(μ,σ2),其中μ为(1)中的平均数,σ2=14 400.若该脐橙基地参与销售的购物群约有1 000个,销售的脐橙在[256,616](单位:盒)内的群为“A级群”,销售数量小于256盒的购物群为“B级群”,销售数量大于616盒的购物群为“特级群”,该脐橙基地对每个“特级群”奖励600元,每个“A级群”奖励100元,对“B级群”不奖励,则该脐橙基地大约需要准备多少奖金?(群的个数按四舍五入取整数)
附:若X~N(μ,σ2),则P(μ-σ≤X≤μ+σ)≈0.682 7,P(μ-2σ≤X≤μ+2σ)≈0.954 5,P(μ-3σ≤X≤μ+3σ)≈0.997 3.
[解] (1)由题意得,12+18+m+32+18=100,解得m=20,
则这100个购物群销售脐橙总量的平均数为:(150×12+250×18+
350×20+450×32+550×18)=376.
(2)由题意,μ=376,σ=120,则256=μ-σ,616=μ+2σ,
故P(256≤X≤616)=P(μ-σ≤X≤μ+2σ)=×P(μ-σ≤X≤μ+σ)+×P(μ-2σ≤X≤μ+2σ)≈×0.682 7+×0.954 5=0.818 6,
故“A级群”约有1 000×0.818 6=818.6≈819(个),
P(X>616)=P(X>μ+2σ)=[1-P(μ-2σ≤X≤μ+2σ)]≈(1-0.954 5)≈0.023,
故“特级群”约有1 000×0.023=23(个),
则依题意,需要资金为819×100+23×600=95 700(元),即该脐橙基地大约需要准备95 700元.
反思领悟 解答正态分布的实际应用题,其关键是利用图象的对称性,由μ,σ把分布区间转化为3σ特殊区间,从而求出概率.在此过程中用到转化和数形结合思想.
进阶训练(十四) 概率模型的辨识与应用
1.已知某公司生产的风干牛肉干是按包销售的,每包牛肉干的质量M(单位:g)服从正态分布N(250,σ2),且P(M<248)=0.1.
(1)若从公司销售的牛肉干中随机选取3包,求这3包中恰有2包质量不小于248 g的概率;
(2)若从公司销售的牛肉干中随机选取K(K为正整数)包,记质量在248 g~252 g的包数为X,且D(X)>320,求K的最小值.
题号
1
3
5
2
4
[解] (1)因为P(M<248)=0.1,所以P(M≥248)=1-0.1=0.9,
则这3包中恰有2包质量不小于248 g的概率为×0.92×0.1=0.243.
(2)因为P(M<248)=0.1,所以P(248<M<252)=(0.5-0.1)×2=0.8.
依题意可得 X~B(K,0.8),
所以D(X)=K×0.8×(1-0.8)=0.16K,
因为D(X)>320,所以K>2 000,
又K为正整数,所以K的最小值为2 001.
题号
1
3
5
2
4
2.(2024·眉山市东坡区期末)眉山市位于四川西南,有“千载诗书城,人文第一州”的美誉,这里是大文豪苏轼、苏洵、苏辙的故乡,也是人们旅游的好地方.在今年的国庆黄金周,为了丰富游客的文化生活,每天在东坡故里三苏祠举行“三苏文化”知识竞赛.已知甲、乙两队参赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为,乙队中3人答对的概率分别为,且各人回答正确与否相互之间没有影响.
(1)分别求甲队总得分为0分,2分的概率;
(2)求甲队得2分,乙队得1分的概率.
题号
1
3
5
2
4
[解] (1)记“甲队总得分为0分”为事件A,“甲队总得分为2分”为事件B,
甲队总得分为0分,即甲队三人都回答错误,
其概率P(A)==.
甲队总得分为2分,即甲队三人中有1人答错,其余两人答对,
其概率P(B)==.
题号
1
3
5
2
4
(2)记“乙队得1分”为事件C,“甲队得2分,乙队得1分”为事件D,
事件C即乙队三人中有2人答错,其余1人答对,
则P(C)==,
甲队得2分,乙队得1分即事件B,C同时发生,
则P(D)=P(B)P(C)==.
题号
1
3
5
2
4
3.(2025·广西玉林统考模拟)某地区期末进行了统一考试,为做好本次考试的评价工作,现从中随机抽取了50名学生的成绩,经统计,这批学生的成绩全部介于40至100之间,将数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,制成了如图所示的频率分布直方图.
题号
1
3
5
2
4
(1)求频率分布直方图中m的值;在这50名学生中用分层随机抽样的方法从成绩在[70,80),[80,90),[90,100]的三组中抽取了11人,再从这11人中随机抽取3人,记X为3人中成绩在[80,90)的人数,求P(X=1);
(2)规定成绩在的为A等级,成绩在[70,90)的为B等级,其他为C等级.以样本估计总体,用频率代替概率.从所有参加考试的同学中随机抽取3人,求获得B等级的人数不少于2的概率.
题号
1
3
5
2
4
[解] (1)∵(0.004+0.022+0.030+0.028+m+0.004)×10=1,
∴m=0.012.
∵成绩在[70,80),[80,90),的频率之比为0.28∶0.12∶0.04=7∶3∶1,
∴抽取的11人中,成绩在[80,90)的人数为11×=3,
∴P(X=1)==.
题号
1
3
5
2
4
(2)用频率估计概率,获得B等级的概率为(0.028+0.012)×10=0.4=,
记抽取的3人中,获得B等级的人数为Y,则Y~,
∴P(Y≥2)=P(Y=2)+P(Y=3)==,即获得B等级的人数不少于2的概率为.
题号
1
3
5
2
4
4.为庆祝建军节的到来,某校举行“强国强军”知识竞赛.该校某班经过层层筛选,还有最后一个参赛名额要在A,B两名学生中产生,该班委设计了一个选拔方案:A,B两名学生各自从6个问题中随机抽取3个问题作答.已知这6个问题中,学生A能正确回答其中的4个问题,而学生B能正确回答每个问题的概率均为.A,B两名学生对每个问题回答正确与否都是相互独立的.
(1)分别求A,B两名学生恰好答对2个问题的概率;
(2)设A答对的题数为X,B答对的题数为Y,若让你投票决定参赛选手,你会选择哪名学生?请说明理由.
题号
1
3
5
2
4
[解] (1)由题意,知A恰好答对2个问题的概率为P1==,
B恰好答对2个问题的概率为
P2==.
题号
1
3
5
2
4
(2)X的可能取值为1,2,3,则P(X=1)==,P(X=2)==,P(X=3)==,所以E(X)=1×+2×+3×=2,
D(X)=(1-2)2×+(2-2)2×+(3-2)2×=.
易知Y~B,所以E(Y)=3×=2,D(Y)=3×=.
因为E(X)=E(Y),D(X)
1
3
5
2
4
5.某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的质量(单位:克),质量的分组区间为[490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图(如图).
(1)根据频率分布直方图,求质量超过505克的产
品数量;
(2)在上述抽取的40件产品中任取2件,设X为质
量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取2件产品,设Y为质量超过
505克的产品数量,求Y的分布列.
题号
1
3
5
2
4
[解] (1)质量超过505克的产品的频率为5×0.05+5×0.01=0.3,
所以质量超过505克的产品数量为40×0.3=12.
(2)质量超过505克的产品数量为12,则质量未超过505克的产品数量为28,X的取值为0,1,2,X服从超几何分布.
P(X=0)==,P(X=1)==,
P(X=2)==,
所以X的分布列为
X 0 1 2
P
题号
1
3
5
2
4
(3)根据样本估计总体的思想,取一件产品,该产品的质量超过505克的概率为=.
从流水线上任取2件产品互不影响,该问题可看成2重伯努利试
验,质量超过505克的件数Y的可能取值为0,1,2,且Y~B,P(Y=k)=,k=0,1,2.
题号
1
3
5
2
4
题号
1
3
5
2
4
所以P(Y=0)==,
P(Y=1)==,
P(Y=2)==.
所以Y的分布列为
Y 0 1 2
P
谢 谢 !
同课章节目录
