《高考快车道》2026版高三一轮总复习数学(基础版)113 第十章 第4课时 列联表与独立性检验 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)113 第十章 第4课时 列联表与独立性检验 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:02 | ||
图片预览







文档简介
(共81张PPT)
第十章 统计与成对数据的统计分析
第4课时 列联表与独立性检验
[考试要求] 1.通过实例,理解2×2列联表的统计意义.
2.通过实例,了解独立性检验及其应用.
考点一 列联表与χ2的计算
1.分类变量
为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.分类变量的取值可以用实数表示.
2.分类变量X,Y的2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
则χ2=.
注:χ2即K2,α即P(K2≥k),xα即k,不同版本教材所用符号有所不同.
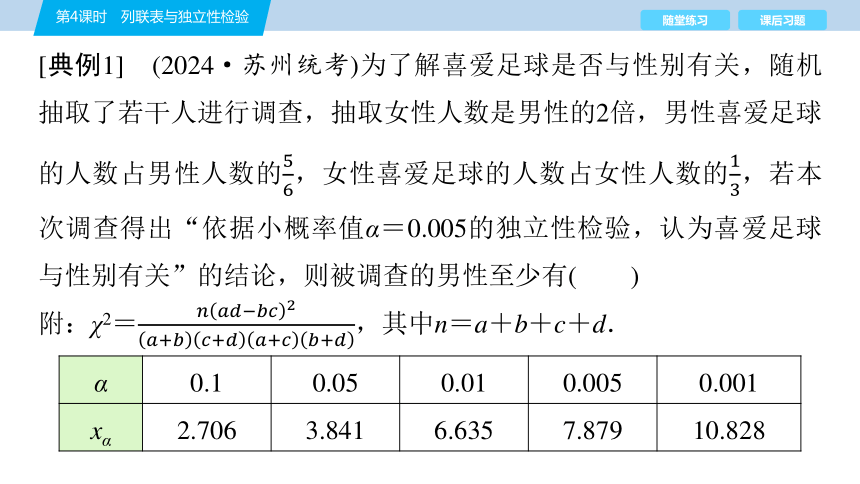
[典例1] (2024·苏州统考)为了解喜爱足球是否与性别有关,随机抽取了若干人进行调查,抽取女性人数是男性的2倍,男性喜爱足球的人数占男性人数的,女性喜爱足球的人数占女性人数的,若本次调查得出“依据小概率值α=0.005的独立性检验,认为喜爱足球与性别有关”的结论,则被调查的男性至少有( )
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
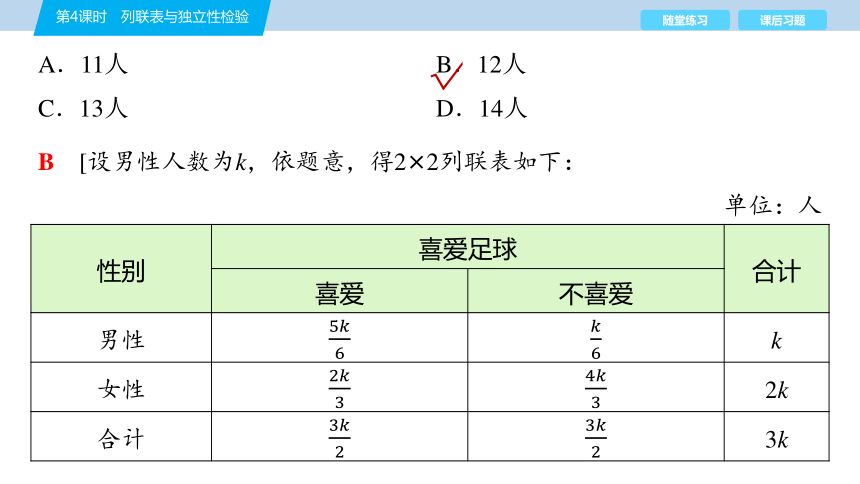
A.11人 B.12人
C.13人 D.14人
√
B [设男性人数为k,依题意,得2×2列联表如下:
单位:人
性别 喜爱足球 合计
喜爱 不喜爱
男性 k
女性 2k
合计 3k
依据列联表中数据计算得到
χ2==,
因为本次调查得出“依据小概率值α=0.005的独立性检验,认为喜爱足球与性别有关”的结论,
于是χ2≥7.879=x0.005,即≥7.879,
解得k≥11.818 5,而k是6的正整数倍,因此kmin=12.]
反思领悟 2×2列联表是4行4列,关键是对涉及的变量分清类别,χ2的计算要准确无误.
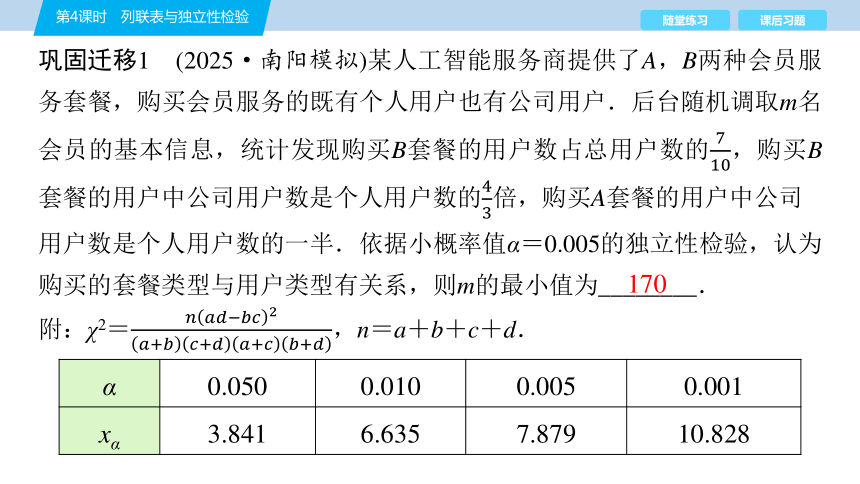
巩固迁移1 (2025·南阳模拟)某人工智能服务商提供了A,B两种会员服务套餐,购买会员服务的既有个人用户也有公司用户.后台随机调取m名
会员的基本信息,统计发现购买B套餐的用户数占总用户数的,购买B套餐的用户中公司用户数是个人用户数的倍,购买A套餐的用户中公司
用户数是个人用户数的一半.依据小概率值α=0.005的独立性检验,认为购买的套餐类型与用户类型有关系,则m的最小值为________.
附:χ2=,n=a+b+c+d.
α 0.050 0.010 0.005 0.001
xα 3.841 6.635 7.879 10.828
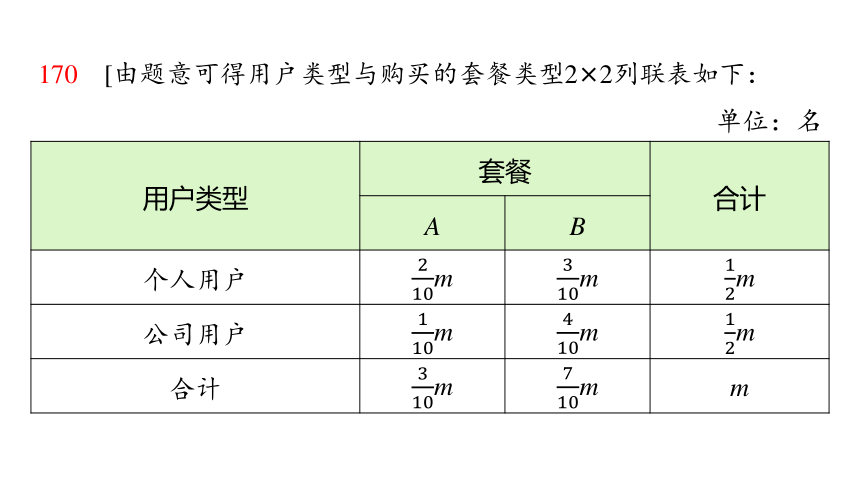
170
170 [由题意可得用户类型与购买的套餐类型2×2列联表如下:
单位:名
用户类型 套餐 合计
A B
个人用户 m m m
公司用户 m m m
合计 m m m
零假设为
H0:购买的套餐类型与用户类型无关.
χ2==,
因为依据小概率值α=0.005的独立性检验,认为购买的套餐类型与用户类型有关,
所以χ2=≥7.879,解得m≥165.459,又因为m必须是10的倍数,所以m的最小值为170.]
考点二 列联表与独立性检验
1.利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
2.χ2独立性检验中几个常用的小概率值和相应的临界值.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
3.两个分类变量之间关联关系的定性分析的方法
(1)利用等高堆积条形图直观判断:
如图,在等高堆积条形图中,下方同一颜色区域的两个高度相差比较明显时,可以判断两个分类变量之间有关联性.
(2)频率分析法:在2×2列联表中,与或与相差越大,两个分类变量有关联的可能性____.
越大
[典例2] (2025·八省联考)为考察某种药物A对预防疾病B的效果,进行了动物(单位:只)试验,得到如下列联表:
药物 疾病 合计
未患病 患病
未服用 100 80 s
服用 150 70 220
合计 250 t 400
(1)求s,t;
(2)记未服用药物A的动物患疾病B的概率为p,给出p的估计值;
(3)根据小概率值α=0.01的独立性检验,能否认为药物A对预防疾病B有效?
附:χ2=,
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
[解] (1)由列联表知,s=100+80=180,t=80+70=150.
(2)由列联表知,未服用药物A的动物有s=180(只),
未服用药物A且患疾病B的动物有80只,
所以未服用药物A的动物患疾病B的频率为=,
所以未服用药物A的动物患疾病B的概率的估计值为p=.
(3)零假设为H0:药物A对预防疾病B无效.
根据列联表中的数据可求得
χ2=≈6.73>6.635=x0.01.
根据小概率值α=0.01的χ2独立性检验,可以认为H0不成立,
所以在犯错误的概率不超过0.01的情况下,可以认为药物A对预防疾病B有效.
链接·2025高考试题
(2025·全国一卷)为研究某疾病与超声波检查结果的关系,从做过超声波检查的人群中随机调查了1 000人,得到如下列联表:
组别 超声波检查结果 合计
正常 不正常
患该疾病 20 180 200
未患该疾病 780 20 800
合计 800 200 1 000
(1)记超声波检查结果不正常者患该疾病的概率为p,求p的估计值;
(2)根据小概率值α=0.001的独立性检验,分析超声波检查结果是否与患该疾病有关.
附:χ2=,
解:(1)由题表可知,检查结果不正常者有200人,检查结果不正常者中患有该疾病的有180人,
所以由样本估计总体得p==0.9.
(2)零假设H0:超声波检查结果与是否患该疾病无关.
χ2==765.625>10.828,
所以依据小概率值α=0.001的独立性检验,我们推断H0不成立,即认为超声波检查结果与是否患该疾病有关.
反思领悟 如果χ2>xα,则“X与Y有关系”这种推断犯错误的概率不超过α;否则,就认为在犯错误的概率不超过α的前提下不能推断“X与Y有关系”,或者在样本数据中没有足够证据支持结论“X与Y有关系”.
巩固迁移2 (2025·渭南临渭区模拟)为了验证甲、乙两种药物对治疗某种病毒的感染是否有差异,某医学科研单位用两种药物对感染病毒的小白鼠进行药物注射试验.取200只感染病毒的小白鼠,其中100只注射甲药物,另外100只注射乙药物,治疗效果的统计数据如下:
单位:只
药物类型 治疗效果 合计
康复 未康复
甲药物 60 40 100
乙药物 75 25 100
合计 135 65 200
(1)分别估计小白鼠注射甲、乙两种药物康复的概率;
(2)依据小概率值α=0.025的独立性检验,是否认为甲、乙两种药物对治疗该种病毒的感染有差异?
参考公式:χ2=,n=a+b+c+d.
临界值表:
α 0.10 0.05 0.025 0.010 0.005 0.001
xα 2.706 3.841 5.024 6.635 7.879 10.828
[解] (1)由题意可知,注射甲药物的小白鼠共100只,康复的有60
只,故小白鼠注射甲药物康复的频率为P1==,故可估计小白
鼠注射甲药物康复的概率为;
注射乙药物的小白鼠共100只,康复的有75只,故小白鼠注射乙药物
康复的频率为P2==,
故可估计小白鼠注射乙药物康复的概率为.
(2)零假设为
H0:甲、乙两种药物对治疗该种病毒的感染无差异.
由表中的数据可知,χ2=≈5.13,
因为5.13>5.024,
所以依据小概率值α=0.025的独立性检验,推断H0不成立,即认为甲、乙两种药物对治疗该种病毒的感染有差异.
考点三 独立性检验的综合应用
[典例3] 为了解某校学生对科技发明活动的兴趣,随机从该校学生中抽取了
100人进行调查,其中女生中对科技发明活动没兴趣的占女生人数的,男生有5
人表示对科技发明活动没有兴趣.
(1)完成2×2列联表,依据小概率值α=0.025的独立性检验,能否认为该校学生对科技发明活动是否有兴趣与性别有关?
单位:人
性别 兴趣 合计
有兴趣 没兴趣
男生 60
女生
合计
(2)从样本中对科技发明活动没有兴趣的学生按性别用分层随机抽样的方法抽出6名学生,记从这6人中随机抽取3人,抽到的男生人数为X,求X的分布列和期望.
附:χ2=,n=a+b+c+d.
α 0.10 0.05 0.025 0.010
xα 2.706 3.841 5.024 6.635
[解] (1)由题述列联表可知,男生合计60人,
所以女生合计100-60=40(人),
由题意,女生中对科技发明活动没兴趣、有兴趣的分别有40×=
10(人),40-10=30(人),
男生中对科技发明活动没兴趣、有兴趣的分别有5人,60-5=55(人),
由此可以得到完整列联表如下:
单位:人
性别 兴趣 合计
有兴趣 没兴趣
男生 55 5 60
女生 30 10 40
合计 85 15 100
零假设为
H0:该校学生对科技发明活动是否有兴趣与性别无关.
χ2=
=≈5.229>5.024,
所以依据小概率值α=0.025的独立性检验,推断H0不成立,即认为该校学生对科技发明活动是否有兴趣与性别有关.
(2)由题意,抽出的6名学生中,男生、女生分别有6×=2(人),6×=4(人),
若从这6人中随机抽取3人,抽到的男生人数为X,则X的所有可能取值为0,1,2,
P(X=0)==,P(X=1)==,P(X=2)==,
所以X的分布列为
X 0 1 2
P
所以E(X)=0×+1×+2×=1.
反思领悟 独立性检验的一般步骤
(1)根据样本数据完成2×2列联表;
(2)根据公式χ2=计算;
(3)比较χ2与临界值的大小关系,作统计推断.
巩固迁移3 第33届夏季奥林匹克运动会于2024年7月26日在法国巴黎开幕.某体育博主为调查大学生对巴黎奥运会的了解情况,在某大学随机抽取了200名大学生(其中男生和女生各100名)提问他们有关奥运会的问题,完全答对的认为了解奥运会,否则认为不了解奥运会,得到如下2×2列联表:
单位:人
情况 性别 合计
男生 女生
了解奥运会 70 50 120
不了解奥运会 30 50 80
合计 100 100 200
(1)根据2×2列联表,依据小概率值α=0.01的独立性检验,能否认为大学生是否了解奥运会与性别有关?
(2)将频率视为概率,用样本估计总体,若从该校大学生中随机抽取3人调查他们对奥运会的了解情况,记抽取的3人中了解奥运会的人数为X,求X的分布列和数学期望.
附: χ2=,其中n=a+b+c+d.
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
[解] (1)零假设为
H0:大学生是否了解奥运会与性别无关.
由题意,χ2=≈8.333>6.635.
依据小概率值α=0.01的独立性检验,推断H0不成立,即认为大学生是否了解奥运会与性别有关.
(2)从该校大学生中随机抽取1人,其了解奥运会的概率为=,所以X~B,由题意知,X的可能取值为0,1,2,3,
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
所以X的分布列为
X 0 1 2 3
P
所以E(X)=0×+1×+2×+3×=.
【教用·备选题】
(2025·贵州黔东南模拟)二十四节气起源于黄河流域,是古代中国劳动人民长期经验的积累和智慧的结晶.其中“立冬小雪十一月,大雪冬至迎新年”就是描述二十四节气农历11月和12月的节气口诀.某中学为调查本校学生对二十四节气的了解情况,
组织测试活动,按照性别用分层随机
抽样的方法抽取了150名学生进行答题,
其中男生占60%,记录其性别和是否全
部答对的情况,得到如图所示的等高堆积条形图.
(1)完成下面的2×2列联表,依据小概率值α=0.05的独立性检验,能否认为是否全部答对与性别有关?
单位:人
性别 对错 合计
完全答对 部分答对
男生
女生
合计
(2)从参加测试的女生中选取一人继续回答甲、乙两道题目,已知该女生答对甲、乙两道题目的概率分别是,记该女生答对题目的个数为X,求X的分布列和数学期望.
附:χ2=,其中n=a+b+c+d.
α 0.100 0.050 0.010 0.005
xα 2.706 3.841 6.635 7.879
[解] (1)按照性别用分层随机抽样方法抽取出的男生人数为150×60%=90,则抽取的女生人数为150-90=60.
抽取的女生中全部答对的人数为60×0.7=42,部分答对的人数为60-42=18,
抽取的男生中全部答对的人数为90×0.5=45,部分答对的人数为90-45=45.
由此得到完整的列联表如下.
单位:人
性别 对错 合计
完全答对 部分答对
男生 45 45 90
女生 42 18 60
合计 87 63 150
零假设为
H0:是否全部答对与性别无关.
χ2=≈5.911>3.841,
依据小概率值α=0.05的独立性检验,推断H0不成立,即认为是否全部答对与性别有关.
(2)由题意可得,X的可能取值为0,1,2,
P(X=0)==,
P(X=1)==,
P(X=2)==,
则X的分布列为
所以E(X)=0×+1×+2×=.
X 0 1 2
P
随堂练习
1.某科研机构为了研究中年人秃发与心脏病是否有关,随机调查了一些中年人的情况,具体数据如下表:
单位:人
中年人 疾病 合计
心脏病 无心脏病
秃发 20 300 320
不秃发 5 450 455
合计 25 750 775
根据表中数据得到χ2≈15.968,因为χ2>10.828,所以断定秃发与心脏病有关系.则这种判断出错的可能性不大于( )
A.0.001 B.0.05
C.0.025 D.0.01
√
A [因为χ2>10.828=x0.001,所以判断出错的可能性不大于0.001.]
2.(2025·盐城模拟)根据分类变量Ⅰ与Ⅱ的统计数据,计算得到χ2=2.954,则( )
√
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
A.变量Ⅰ与Ⅱ有关联
B.变量Ⅰ与Ⅱ有关联,这个结论犯错误的概率不超过0.1
C.变量Ⅰ与Ⅱ无关联
D.变量Ⅰ与Ⅱ无关联,这个结论犯错误的概率不超过0.1
B [零假设为
H0:变量Ⅰ与Ⅱ无关联,
因为χ2=2.954>2.706=x0.1,
所以依据α=0.1的独立性检验,我们推断H0不成立,即认为变量Ⅰ与Ⅱ有关联,
这个结论犯错误的概率不超过0.1.故选B.]
3.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样的方法在校园内调查了120位学生,得到如下2×2列联表:
单位:人
体育锻炼 性别 合计
男 女
爱好 a b 73
不爱好 c 25
合计 74
则a-b-c=( )
A.7 B.8
C.9 D.10
√
C [由题意得c=120-73-25=22,a=74-22=52,b=73-52=21,所以a-b-c=52-21-22=9.]
课后习题(七十) 列联表与独立性检验
参考数据及公式
χ2=,n=a+b+c+d.
α 0.10 0.05 0.025 0.01 0.005 0.001
xα 2.706 3.841 5.024 6.635 7.879 10.828
1.(人教A版选择性必修第三册P134练习T4改编)某课外兴趣小组通过随机调查,利用2×2列联表和χ2统计量研究数学成绩优秀是否与性别有关.计算得χ2=6.748,经查阅临界值表知χ2≥6.635=x0.01,则下列判断正确的是( )
A.每100个数学成绩优秀的人中就会有1名是女生
B.若某人数学成绩优秀,那么他为男生的概率是0.010
C.依据小概率值α=0.01的独立性检验,认为“数学成绩优秀与性别无关”
D.在犯错误的概率不超过0.01的前提下认为“数学成绩优秀与性别有关”
√
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
D [因为χ2=6.748>6.635=x0.01,所以依据小概率值α=0.01的独立性检验,认为“数学成绩优秀与性别有关”,即在犯错误的概率不超过0.01的前提下认为数学成绩优秀与性别有关,所以ABC错误.故选D.]
√
题号
1
3
5
2
4
6
8
7
9
10
2.(人教A版选择性必修第三册P133例4改编)在研究吸烟是否对患肺癌有影响的案例中,通过对列联表的数据进行处理,计算得到随机变量χ2≈56.632.在犯错误的概率不超过0.001的前提下,下面说法正确的是( )
A.因为随机变量χ2>10.828=x0.001,所以“吸烟与患肺癌有关系”,并且这个结论犯错误的概率不超过0.001
B.因为随机变量χ2>10.828,所以“吸烟与患肺癌有关系”,并且这个结论犯错误的概率不低于0.001
C.因为随机变量χ2>10.828,所以“吸烟与患肺癌没有关系”,并且这个结论犯错误的概率不超过0.001
D.因为随机变量χ2>10.828,所以“吸烟与患肺癌没有关系”,并且这个结论犯错误的概率不低于0.001
题号
1
3
5
2
4
6
8
7
9
10
A [由题意知,通过对列联表的数据进行处理,计算得到随机变量χ2≈56.632>10.828=x0.001,所以在犯错误的概率不超过0.001的前提下,认为吸烟与患肺癌有关系.]
题号
1
3
5
2
4
6
8
7
9
10
3.(人教A版选择性必修第三册P132例3改编)为调查某城市居民对冰雪运动的了解情况,随机抽取了该市120名市民进行统计,得到如下2×2列联表:
单位:人
冰雪运动 性别 合计
男性 女性
了解 m p 70
不了解 n q 50
合计 60 60 120
已知从参与调查的男性市民中随机选取1名,抽到了解冰雪运动的概率为.根据列联表数据,求得χ2≈________(保留3位小数).
3.429 [由题意知,m=60×=40,所以n=60-m=20,p=70-m=30,q=50-n=30,
则χ2=≈3.429.]
题号
1
3
5
2
4
6
8
7
9
10
3.429
题号
1
3
5
2
4
6
8
7
9
10
4.(2025·山东烟台模拟)某校为了研究“学生的性别”和“对待某一活动的态度”是否有关,运用2×2列联表进行独立性检验.经计算χ2=7.069,则认为“学生性别与支持某项活动有关系”的犯错误的概率不超过( )
A.0.1% B.1%
C.99% D.99.9%
√
题号
1
3
5
2
4
6
8
7
9
10
B [∵χ2=7.069>6.635=x0.01,
∴认为“学生性别与支持某项活动有关系”的犯错误的概率不超过1%.]
题号
1
3
5
2
4
6
8
7
9
10
5.(2024·银川兴庆区一模)有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
单位:人
班级 数学成绩 合计
优秀 非优秀
甲班 10 b
乙班 c 30
合计
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法
正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,依据小概率值α=0.025的独立性检验,认为成绩与班级有关
D.根据列联表中的数据,依据小概率值α=0.025的独立性检验,不能认为成绩与班级有关
√
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
C [由题意知,成绩优秀的学生人数是105×=30,
成绩非优秀的学生人数是75,所以c=20,b=45,A,B错误;
零假设为H0:成绩与班级无关.
根据列联表中的数据,
得到χ2=≈6.109>5.024=x0.025,
因此依据小概率值α=0.025的独立性检验,推断H0不成立,即认为成绩与班级有关.
故C正确、D错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
6.(多选)(2025·鞍山模拟)某校团委对“学生性别和喜欢篮球是否有关”作了调查,其中被调查的男、女生人数相同,男生喜欢篮球的人数占男生人数的,女生喜欢篮球的人数占女生人数的,若依据小概率值α=0.1的独立性检验,认为是否喜欢篮球和性别有关,则调查人数中男生可能有( )
A.20人 B.30人
C.35人 D.40人
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
BCD [设男生可能有x人,由被调查的男、女生人数相同知女生也有x人,填写列联表如下:
单位:人
性别 篮球 合计
喜欢 不喜欢
男生 x x x
女生 x x x
合计 x x 2x
若依据小概率值α=0.1的独立性检验,认为是否喜欢篮球和性别有关,则χ2≥2.706,
即χ2==x≥2.706,解得x≥28.413,
由题意知x>0,且x是5的整数倍,所以30,35,40都满足题意.
故选BCD.]
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
7.(多选)(2024·湛江一模)某养老院有110名老人,经过一年的跟踪调查,过去的一年中他们是否患过某流行疾病和性别的相关数据如下表所示:
单位:人
性别 是否患过某流行疾病 合计
患过该疾病 未患过该疾病
男性 a=20 b a+b
女性 c d=50 c+d
合计 a+c 80 110
下列说法正确的有( )
参考公式:χ2=,其中n=a+b+c+d.
附表:
α 0.1 0.05 0.025 0.01 0.001
xα 2.706 3.841 5.024 6.635 10.828
题号
1
3
5
2
4
6
8
7
9
10
A.>
B.χ2>6.635
C.依据小概率值α=0.01的独立性检验,认为是否患过该流行疾病与性别有关联
D.根据小概率值α=0.01的独立性检验,没有充分的证据推断是否患过该流行疾病与性别有关联
题号
1
3
5
2
4
6
8
7
9
10
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
ABC [由列联表知,a+c=110-80=30,所以c=10,b=30,
所以====,
所以>,选项A正确;
计算χ2=≈7.486>6.635,选项B正确;
依据小概率值α=0.01的独立性检验,认为是否患过该流行疾病与性别有关联,选项C正确,D错误.
故选ABC.]
题号
1
3
5
2
4
6
8
7
9
10
8.(2024·保定模拟)下面是一个2×2列联表,则表中a,b处的值分别为________.
x y 合计
y1 y2
x1 a 21 73
x2 2 25 27
合计 b 46 100
52,54
题号
1
3
5
2
4
6
8
7
9
10
52,54 [根据列联表可知,∵a+21=73,∴a=52.又∵a+2=b,∴b=54.]
题号
1
3
5
2
4
6
8
7
9
10
9.(2024·信阳期末)为了研究高三学生的性别和身高是否大于
170 cm的关联性,调查了高三学生200名,得到如下列联表:
单位:人
性别 身高 合计
低于170 cm 不低于170 cm
女 80 20 100
男 30 70 100
合计 110 90 200
根据列联表的数据,计算得χ2≈________;依据小概率值α=0.001的独立性检验,________(填“能”或“不能”)认为“高三学生的性别和身高有关联”.
题号
1
3
5
2
4
6
8
7
9
10
50.505
能
题号
1
3
5
2
4
6
8
7
9
10
50.505 能 [零假设为
H0:高三学生的性别和身高无关联.
根据列联表中的数据,计算χ2=≈
50.505>10.828,
依据小概率值α=0.001的独立性检验,可以推断H0不成立,即能认为高三学生的性别和身高有关联.]
10.(2025·福州模拟)甲、乙两所学校高三年级分别有1 000人、1 100人,为了了解两所学校全体高三年级学生数学测试情况,采用分层随机抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了如下的频数分布统计表,规定考试成绩在[120,150]内为优秀.
分组 [70,80) [80,90) [90,100) [100,110)
甲校频数 1 2 9 8
乙校频数 2 3 10 15
题号
1
3
5
2
4
6
8
7
9
10
(1)计算x,y的值;
分组 [110,120) [120,130) [130,140) [140,150]
甲校频数 10 10 x 3
乙校频数 15 y 3 1
题号
1
3
5
2
4
6
8
7
9
10
(2)由以上统计数据填写下面2×2列联表,依据小概率值α=0.025的独立性检验,能否认为两个学校的数学成绩有差异?
单位:人
数学成绩 学校 合计
甲校 乙校
优秀
非优秀
合计
题号
1
3
5
2
4
6
8
7
9
10
[解] (1)由题可知,采用分层随机抽样方法共抽取105人,1 000∶1 100=10∶11,所以甲校抽取105×=50(人),乙校抽取105×=55(人),
故1+2+9+8+10+10+x+3=50,解得x=7,
2+3+10+15+15+y+3+1=55,解得y=6.
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
(2)由频数分布表可得2×2列联表为
单位:人
数学成绩 学校 合计
甲校 乙校
优秀 20 10 30
非优秀 30 45 75
合计 50 55 105
零假设为
H0:两个学校的数学成绩无差异.
χ2=≈6.109>5.024=x0.025,
依据小概率值α=0.025的独立性检验,我们推断H0不成立,即认为两个学校的数学成绩有差异.
题号
1
3
5
2
4
6
8
7
9
10
谢 谢 !
第十章 统计与成对数据的统计分析
第4课时 列联表与独立性检验
[考试要求] 1.通过实例,理解2×2列联表的统计意义.
2.通过实例,了解独立性检验及其应用.
考点一 列联表与χ2的计算
1.分类变量
为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.分类变量的取值可以用实数表示.
2.分类变量X,Y的2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
则χ2=.
注:χ2即K2,α即P(K2≥k),xα即k,不同版本教材所用符号有所不同.
[典例1] (2024·苏州统考)为了解喜爱足球是否与性别有关,随机抽取了若干人进行调查,抽取女性人数是男性的2倍,男性喜爱足球的人数占男性人数的,女性喜爱足球的人数占女性人数的,若本次调查得出“依据小概率值α=0.005的独立性检验,认为喜爱足球与性别有关”的结论,则被调查的男性至少有( )
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
A.11人 B.12人
C.13人 D.14人
√
B [设男性人数为k,依题意,得2×2列联表如下:
单位:人
性别 喜爱足球 合计
喜爱 不喜爱
男性 k
女性 2k
合计 3k
依据列联表中数据计算得到
χ2==,
因为本次调查得出“依据小概率值α=0.005的独立性检验,认为喜爱足球与性别有关”的结论,
于是χ2≥7.879=x0.005,即≥7.879,
解得k≥11.818 5,而k是6的正整数倍,因此kmin=12.]
反思领悟 2×2列联表是4行4列,关键是对涉及的变量分清类别,χ2的计算要准确无误.
巩固迁移1 (2025·南阳模拟)某人工智能服务商提供了A,B两种会员服务套餐,购买会员服务的既有个人用户也有公司用户.后台随机调取m名
会员的基本信息,统计发现购买B套餐的用户数占总用户数的,购买B套餐的用户中公司用户数是个人用户数的倍,购买A套餐的用户中公司
用户数是个人用户数的一半.依据小概率值α=0.005的独立性检验,认为购买的套餐类型与用户类型有关系,则m的最小值为________.
附:χ2=,n=a+b+c+d.
α 0.050 0.010 0.005 0.001
xα 3.841 6.635 7.879 10.828
170
170 [由题意可得用户类型与购买的套餐类型2×2列联表如下:
单位:名
用户类型 套餐 合计
A B
个人用户 m m m
公司用户 m m m
合计 m m m
零假设为
H0:购买的套餐类型与用户类型无关.
χ2==,
因为依据小概率值α=0.005的独立性检验,认为购买的套餐类型与用户类型有关,
所以χ2=≥7.879,解得m≥165.459,又因为m必须是10的倍数,所以m的最小值为170.]
考点二 列联表与独立性检验
1.利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”,简称独立性检验.
2.χ2独立性检验中几个常用的小概率值和相应的临界值.
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
3.两个分类变量之间关联关系的定性分析的方法
(1)利用等高堆积条形图直观判断:
如图,在等高堆积条形图中,下方同一颜色区域的两个高度相差比较明显时,可以判断两个分类变量之间有关联性.
(2)频率分析法:在2×2列联表中,与或与相差越大,两个分类变量有关联的可能性____.
越大
[典例2] (2025·八省联考)为考察某种药物A对预防疾病B的效果,进行了动物(单位:只)试验,得到如下列联表:
药物 疾病 合计
未患病 患病
未服用 100 80 s
服用 150 70 220
合计 250 t 400
(1)求s,t;
(2)记未服用药物A的动物患疾病B的概率为p,给出p的估计值;
(3)根据小概率值α=0.01的独立性检验,能否认为药物A对预防疾病B有效?
附:χ2=,
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
[解] (1)由列联表知,s=100+80=180,t=80+70=150.
(2)由列联表知,未服用药物A的动物有s=180(只),
未服用药物A且患疾病B的动物有80只,
所以未服用药物A的动物患疾病B的频率为=,
所以未服用药物A的动物患疾病B的概率的估计值为p=.
(3)零假设为H0:药物A对预防疾病B无效.
根据列联表中的数据可求得
χ2=≈6.73>6.635=x0.01.
根据小概率值α=0.01的χ2独立性检验,可以认为H0不成立,
所以在犯错误的概率不超过0.01的情况下,可以认为药物A对预防疾病B有效.
链接·2025高考试题
(2025·全国一卷)为研究某疾病与超声波检查结果的关系,从做过超声波检查的人群中随机调查了1 000人,得到如下列联表:
组别 超声波检查结果 合计
正常 不正常
患该疾病 20 180 200
未患该疾病 780 20 800
合计 800 200 1 000
(1)记超声波检查结果不正常者患该疾病的概率为p,求p的估计值;
(2)根据小概率值α=0.001的独立性检验,分析超声波检查结果是否与患该疾病有关.
附:χ2=,
解:(1)由题表可知,检查结果不正常者有200人,检查结果不正常者中患有该疾病的有180人,
所以由样本估计总体得p==0.9.
(2)零假设H0:超声波检查结果与是否患该疾病无关.
χ2==765.625>10.828,
所以依据小概率值α=0.001的独立性检验,我们推断H0不成立,即认为超声波检查结果与是否患该疾病有关.
反思领悟 如果χ2>xα,则“X与Y有关系”这种推断犯错误的概率不超过α;否则,就认为在犯错误的概率不超过α的前提下不能推断“X与Y有关系”,或者在样本数据中没有足够证据支持结论“X与Y有关系”.
巩固迁移2 (2025·渭南临渭区模拟)为了验证甲、乙两种药物对治疗某种病毒的感染是否有差异,某医学科研单位用两种药物对感染病毒的小白鼠进行药物注射试验.取200只感染病毒的小白鼠,其中100只注射甲药物,另外100只注射乙药物,治疗效果的统计数据如下:
单位:只
药物类型 治疗效果 合计
康复 未康复
甲药物 60 40 100
乙药物 75 25 100
合计 135 65 200
(1)分别估计小白鼠注射甲、乙两种药物康复的概率;
(2)依据小概率值α=0.025的独立性检验,是否认为甲、乙两种药物对治疗该种病毒的感染有差异?
参考公式:χ2=,n=a+b+c+d.
临界值表:
α 0.10 0.05 0.025 0.010 0.005 0.001
xα 2.706 3.841 5.024 6.635 7.879 10.828
[解] (1)由题意可知,注射甲药物的小白鼠共100只,康复的有60
只,故小白鼠注射甲药物康复的频率为P1==,故可估计小白
鼠注射甲药物康复的概率为;
注射乙药物的小白鼠共100只,康复的有75只,故小白鼠注射乙药物
康复的频率为P2==,
故可估计小白鼠注射乙药物康复的概率为.
(2)零假设为
H0:甲、乙两种药物对治疗该种病毒的感染无差异.
由表中的数据可知,χ2=≈5.13,
因为5.13>5.024,
所以依据小概率值α=0.025的独立性检验,推断H0不成立,即认为甲、乙两种药物对治疗该种病毒的感染有差异.
考点三 独立性检验的综合应用
[典例3] 为了解某校学生对科技发明活动的兴趣,随机从该校学生中抽取了
100人进行调查,其中女生中对科技发明活动没兴趣的占女生人数的,男生有5
人表示对科技发明活动没有兴趣.
(1)完成2×2列联表,依据小概率值α=0.025的独立性检验,能否认为该校学生对科技发明活动是否有兴趣与性别有关?
单位:人
性别 兴趣 合计
有兴趣 没兴趣
男生 60
女生
合计
(2)从样本中对科技发明活动没有兴趣的学生按性别用分层随机抽样的方法抽出6名学生,记从这6人中随机抽取3人,抽到的男生人数为X,求X的分布列和期望.
附:χ2=,n=a+b+c+d.
α 0.10 0.05 0.025 0.010
xα 2.706 3.841 5.024 6.635
[解] (1)由题述列联表可知,男生合计60人,
所以女生合计100-60=40(人),
由题意,女生中对科技发明活动没兴趣、有兴趣的分别有40×=
10(人),40-10=30(人),
男生中对科技发明活动没兴趣、有兴趣的分别有5人,60-5=55(人),
由此可以得到完整列联表如下:
单位:人
性别 兴趣 合计
有兴趣 没兴趣
男生 55 5 60
女生 30 10 40
合计 85 15 100
零假设为
H0:该校学生对科技发明活动是否有兴趣与性别无关.
χ2=
=≈5.229>5.024,
所以依据小概率值α=0.025的独立性检验,推断H0不成立,即认为该校学生对科技发明活动是否有兴趣与性别有关.
(2)由题意,抽出的6名学生中,男生、女生分别有6×=2(人),6×=4(人),
若从这6人中随机抽取3人,抽到的男生人数为X,则X的所有可能取值为0,1,2,
P(X=0)==,P(X=1)==,P(X=2)==,
所以X的分布列为
X 0 1 2
P
所以E(X)=0×+1×+2×=1.
反思领悟 独立性检验的一般步骤
(1)根据样本数据完成2×2列联表;
(2)根据公式χ2=计算;
(3)比较χ2与临界值的大小关系,作统计推断.
巩固迁移3 第33届夏季奥林匹克运动会于2024年7月26日在法国巴黎开幕.某体育博主为调查大学生对巴黎奥运会的了解情况,在某大学随机抽取了200名大学生(其中男生和女生各100名)提问他们有关奥运会的问题,完全答对的认为了解奥运会,否则认为不了解奥运会,得到如下2×2列联表:
单位:人
情况 性别 合计
男生 女生
了解奥运会 70 50 120
不了解奥运会 30 50 80
合计 100 100 200
(1)根据2×2列联表,依据小概率值α=0.01的独立性检验,能否认为大学生是否了解奥运会与性别有关?
(2)将频率视为概率,用样本估计总体,若从该校大学生中随机抽取3人调查他们对奥运会的了解情况,记抽取的3人中了解奥运会的人数为X,求X的分布列和数学期望.
附: χ2=,其中n=a+b+c+d.
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
[解] (1)零假设为
H0:大学生是否了解奥运会与性别无关.
由题意,χ2=≈8.333>6.635.
依据小概率值α=0.01的独立性检验,推断H0不成立,即认为大学生是否了解奥运会与性别有关.
(2)从该校大学生中随机抽取1人,其了解奥运会的概率为=,所以X~B,由题意知,X的可能取值为0,1,2,3,
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
所以X的分布列为
X 0 1 2 3
P
所以E(X)=0×+1×+2×+3×=.
【教用·备选题】
(2025·贵州黔东南模拟)二十四节气起源于黄河流域,是古代中国劳动人民长期经验的积累和智慧的结晶.其中“立冬小雪十一月,大雪冬至迎新年”就是描述二十四节气农历11月和12月的节气口诀.某中学为调查本校学生对二十四节气的了解情况,
组织测试活动,按照性别用分层随机
抽样的方法抽取了150名学生进行答题,
其中男生占60%,记录其性别和是否全
部答对的情况,得到如图所示的等高堆积条形图.
(1)完成下面的2×2列联表,依据小概率值α=0.05的独立性检验,能否认为是否全部答对与性别有关?
单位:人
性别 对错 合计
完全答对 部分答对
男生
女生
合计
(2)从参加测试的女生中选取一人继续回答甲、乙两道题目,已知该女生答对甲、乙两道题目的概率分别是,记该女生答对题目的个数为X,求X的分布列和数学期望.
附:χ2=,其中n=a+b+c+d.
α 0.100 0.050 0.010 0.005
xα 2.706 3.841 6.635 7.879
[解] (1)按照性别用分层随机抽样方法抽取出的男生人数为150×60%=90,则抽取的女生人数为150-90=60.
抽取的女生中全部答对的人数为60×0.7=42,部分答对的人数为60-42=18,
抽取的男生中全部答对的人数为90×0.5=45,部分答对的人数为90-45=45.
由此得到完整的列联表如下.
单位:人
性别 对错 合计
完全答对 部分答对
男生 45 45 90
女生 42 18 60
合计 87 63 150
零假设为
H0:是否全部答对与性别无关.
χ2=≈5.911>3.841,
依据小概率值α=0.05的独立性检验,推断H0不成立,即认为是否全部答对与性别有关.
(2)由题意可得,X的可能取值为0,1,2,
P(X=0)==,
P(X=1)==,
P(X=2)==,
则X的分布列为
所以E(X)=0×+1×+2×=.
X 0 1 2
P
随堂练习
1.某科研机构为了研究中年人秃发与心脏病是否有关,随机调查了一些中年人的情况,具体数据如下表:
单位:人
中年人 疾病 合计
心脏病 无心脏病
秃发 20 300 320
不秃发 5 450 455
合计 25 750 775
根据表中数据得到χ2≈15.968,因为χ2>10.828,所以断定秃发与心脏病有关系.则这种判断出错的可能性不大于( )
A.0.001 B.0.05
C.0.025 D.0.01
√
A [因为χ2>10.828=x0.001,所以判断出错的可能性不大于0.001.]
2.(2025·盐城模拟)根据分类变量Ⅰ与Ⅱ的统计数据,计算得到χ2=2.954,则( )
√
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
A.变量Ⅰ与Ⅱ有关联
B.变量Ⅰ与Ⅱ有关联,这个结论犯错误的概率不超过0.1
C.变量Ⅰ与Ⅱ无关联
D.变量Ⅰ与Ⅱ无关联,这个结论犯错误的概率不超过0.1
B [零假设为
H0:变量Ⅰ与Ⅱ无关联,
因为χ2=2.954>2.706=x0.1,
所以依据α=0.1的独立性检验,我们推断H0不成立,即认为变量Ⅰ与Ⅱ有关联,
这个结论犯错误的概率不超过0.1.故选B.]
3.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样的方法在校园内调查了120位学生,得到如下2×2列联表:
单位:人
体育锻炼 性别 合计
男 女
爱好 a b 73
不爱好 c 25
合计 74
则a-b-c=( )
A.7 B.8
C.9 D.10
√
C [由题意得c=120-73-25=22,a=74-22=52,b=73-52=21,所以a-b-c=52-21-22=9.]
课后习题(七十) 列联表与独立性检验
参考数据及公式
χ2=,n=a+b+c+d.
α 0.10 0.05 0.025 0.01 0.005 0.001
xα 2.706 3.841 5.024 6.635 7.879 10.828
1.(人教A版选择性必修第三册P134练习T4改编)某课外兴趣小组通过随机调查,利用2×2列联表和χ2统计量研究数学成绩优秀是否与性别有关.计算得χ2=6.748,经查阅临界值表知χ2≥6.635=x0.01,则下列判断正确的是( )
A.每100个数学成绩优秀的人中就会有1名是女生
B.若某人数学成绩优秀,那么他为男生的概率是0.010
C.依据小概率值α=0.01的独立性检验,认为“数学成绩优秀与性别无关”
D.在犯错误的概率不超过0.01的前提下认为“数学成绩优秀与性别有关”
√
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
D [因为χ2=6.748>6.635=x0.01,所以依据小概率值α=0.01的独立性检验,认为“数学成绩优秀与性别有关”,即在犯错误的概率不超过0.01的前提下认为数学成绩优秀与性别有关,所以ABC错误.故选D.]
√
题号
1
3
5
2
4
6
8
7
9
10
2.(人教A版选择性必修第三册P133例4改编)在研究吸烟是否对患肺癌有影响的案例中,通过对列联表的数据进行处理,计算得到随机变量χ2≈56.632.在犯错误的概率不超过0.001的前提下,下面说法正确的是( )
A.因为随机变量χ2>10.828=x0.001,所以“吸烟与患肺癌有关系”,并且这个结论犯错误的概率不超过0.001
B.因为随机变量χ2>10.828,所以“吸烟与患肺癌有关系”,并且这个结论犯错误的概率不低于0.001
C.因为随机变量χ2>10.828,所以“吸烟与患肺癌没有关系”,并且这个结论犯错误的概率不超过0.001
D.因为随机变量χ2>10.828,所以“吸烟与患肺癌没有关系”,并且这个结论犯错误的概率不低于0.001
题号
1
3
5
2
4
6
8
7
9
10
A [由题意知,通过对列联表的数据进行处理,计算得到随机变量χ2≈56.632>10.828=x0.001,所以在犯错误的概率不超过0.001的前提下,认为吸烟与患肺癌有关系.]
题号
1
3
5
2
4
6
8
7
9
10
3.(人教A版选择性必修第三册P132例3改编)为调查某城市居民对冰雪运动的了解情况,随机抽取了该市120名市民进行统计,得到如下2×2列联表:
单位:人
冰雪运动 性别 合计
男性 女性
了解 m p 70
不了解 n q 50
合计 60 60 120
已知从参与调查的男性市民中随机选取1名,抽到了解冰雪运动的概率为.根据列联表数据,求得χ2≈________(保留3位小数).
3.429 [由题意知,m=60×=40,所以n=60-m=20,p=70-m=30,q=50-n=30,
则χ2=≈3.429.]
题号
1
3
5
2
4
6
8
7
9
10
3.429
题号
1
3
5
2
4
6
8
7
9
10
4.(2025·山东烟台模拟)某校为了研究“学生的性别”和“对待某一活动的态度”是否有关,运用2×2列联表进行独立性检验.经计算χ2=7.069,则认为“学生性别与支持某项活动有关系”的犯错误的概率不超过( )
A.0.1% B.1%
C.99% D.99.9%
√
题号
1
3
5
2
4
6
8
7
9
10
B [∵χ2=7.069>6.635=x0.01,
∴认为“学生性别与支持某项活动有关系”的犯错误的概率不超过1%.]
题号
1
3
5
2
4
6
8
7
9
10
5.(2024·银川兴庆区一模)有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
单位:人
班级 数学成绩 合计
优秀 非优秀
甲班 10 b
乙班 c 30
合计
已知在全部105人中随机抽取1人,成绩优秀的概率为,则下列说法
正确的是( )
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,依据小概率值α=0.025的独立性检验,认为成绩与班级有关
D.根据列联表中的数据,依据小概率值α=0.025的独立性检验,不能认为成绩与班级有关
√
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
C [由题意知,成绩优秀的学生人数是105×=30,
成绩非优秀的学生人数是75,所以c=20,b=45,A,B错误;
零假设为H0:成绩与班级无关.
根据列联表中的数据,
得到χ2=≈6.109>5.024=x0.025,
因此依据小概率值α=0.025的独立性检验,推断H0不成立,即认为成绩与班级有关.
故C正确、D错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
6.(多选)(2025·鞍山模拟)某校团委对“学生性别和喜欢篮球是否有关”作了调查,其中被调查的男、女生人数相同,男生喜欢篮球的人数占男生人数的,女生喜欢篮球的人数占女生人数的,若依据小概率值α=0.1的独立性检验,认为是否喜欢篮球和性别有关,则调查人数中男生可能有( )
A.20人 B.30人
C.35人 D.40人
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
BCD [设男生可能有x人,由被调查的男、女生人数相同知女生也有x人,填写列联表如下:
单位:人
性别 篮球 合计
喜欢 不喜欢
男生 x x x
女生 x x x
合计 x x 2x
若依据小概率值α=0.1的独立性检验,认为是否喜欢篮球和性别有关,则χ2≥2.706,
即χ2==x≥2.706,解得x≥28.413,
由题意知x>0,且x是5的整数倍,所以30,35,40都满足题意.
故选BCD.]
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
7.(多选)(2024·湛江一模)某养老院有110名老人,经过一年的跟踪调查,过去的一年中他们是否患过某流行疾病和性别的相关数据如下表所示:
单位:人
性别 是否患过某流行疾病 合计
患过该疾病 未患过该疾病
男性 a=20 b a+b
女性 c d=50 c+d
合计 a+c 80 110
下列说法正确的有( )
参考公式:χ2=,其中n=a+b+c+d.
附表:
α 0.1 0.05 0.025 0.01 0.001
xα 2.706 3.841 5.024 6.635 10.828
题号
1
3
5
2
4
6
8
7
9
10
A.>
B.χ2>6.635
C.依据小概率值α=0.01的独立性检验,认为是否患过该流行疾病与性别有关联
D.根据小概率值α=0.01的独立性检验,没有充分的证据推断是否患过该流行疾病与性别有关联
题号
1
3
5
2
4
6
8
7
9
10
√
√
√
题号
1
3
5
2
4
6
8
7
9
10
ABC [由列联表知,a+c=110-80=30,所以c=10,b=30,
所以====,
所以>,选项A正确;
计算χ2=≈7.486>6.635,选项B正确;
依据小概率值α=0.01的独立性检验,认为是否患过该流行疾病与性别有关联,选项C正确,D错误.
故选ABC.]
题号
1
3
5
2
4
6
8
7
9
10
8.(2024·保定模拟)下面是一个2×2列联表,则表中a,b处的值分别为________.
x y 合计
y1 y2
x1 a 21 73
x2 2 25 27
合计 b 46 100
52,54
题号
1
3
5
2
4
6
8
7
9
10
52,54 [根据列联表可知,∵a+21=73,∴a=52.又∵a+2=b,∴b=54.]
题号
1
3
5
2
4
6
8
7
9
10
9.(2024·信阳期末)为了研究高三学生的性别和身高是否大于
170 cm的关联性,调查了高三学生200名,得到如下列联表:
单位:人
性别 身高 合计
低于170 cm 不低于170 cm
女 80 20 100
男 30 70 100
合计 110 90 200
根据列联表的数据,计算得χ2≈________;依据小概率值α=0.001的独立性检验,________(填“能”或“不能”)认为“高三学生的性别和身高有关联”.
题号
1
3
5
2
4
6
8
7
9
10
50.505
能
题号
1
3
5
2
4
6
8
7
9
10
50.505 能 [零假设为
H0:高三学生的性别和身高无关联.
根据列联表中的数据,计算χ2=≈
50.505>10.828,
依据小概率值α=0.001的独立性检验,可以推断H0不成立,即能认为高三学生的性别和身高有关联.]
10.(2025·福州模拟)甲、乙两所学校高三年级分别有1 000人、1 100人,为了了解两所学校全体高三年级学生数学测试情况,采用分层随机抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了如下的频数分布统计表,规定考试成绩在[120,150]内为优秀.
分组 [70,80) [80,90) [90,100) [100,110)
甲校频数 1 2 9 8
乙校频数 2 3 10 15
题号
1
3
5
2
4
6
8
7
9
10
(1)计算x,y的值;
分组 [110,120) [120,130) [130,140) [140,150]
甲校频数 10 10 x 3
乙校频数 15 y 3 1
题号
1
3
5
2
4
6
8
7
9
10
(2)由以上统计数据填写下面2×2列联表,依据小概率值α=0.025的独立性检验,能否认为两个学校的数学成绩有差异?
单位:人
数学成绩 学校 合计
甲校 乙校
优秀
非优秀
合计
题号
1
3
5
2
4
6
8
7
9
10
[解] (1)由题可知,采用分层随机抽样方法共抽取105人,1 000∶1 100=10∶11,所以甲校抽取105×=50(人),乙校抽取105×=55(人),
故1+2+9+8+10+10+x+3=50,解得x=7,
2+3+10+15+15+y+3+1=55,解得y=6.
题号
1
3
5
2
4
6
8
7
9
10
题号
1
3
5
2
4
6
8
7
9
10
(2)由频数分布表可得2×2列联表为
单位:人
数学成绩 学校 合计
甲校 乙校
优秀 20 10 30
非优秀 30 45 75
合计 50 55 105
零假设为
H0:两个学校的数学成绩无差异.
χ2=≈6.109>5.024=x0.025,
依据小概率值α=0.025的独立性检验,我们推断H0不成立,即认为两个学校的数学成绩有差异.
题号
1
3
5
2
4
6
8
7
9
10
谢 谢 !
同课章节目录
