《高考快车道》2026版高三一轮总复习数学(基础版)114 第十章 思维进阶15 概率、统计的交汇问题 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)114 第十章 思维进阶15 概率、统计的交汇问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:02 | ||
图片预览







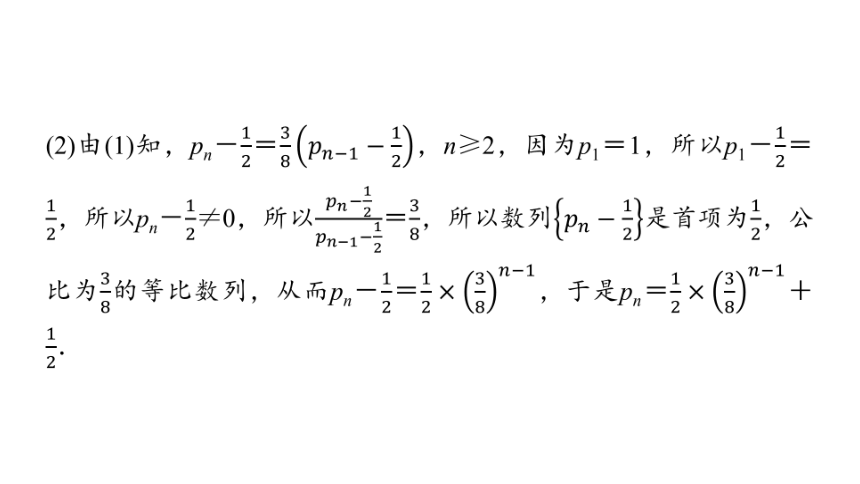




文档简介
(共51张PPT)
第十章 统计与成对数据的统计分析
思维进阶15 概率、统计的交汇问题
近几年高考特别注重对概率和统计结合、概率和其他知识(如数列与函数)结合的综合考查,通常以实际问题为背景,通过构建数学模型,突出考查统计与概率思想、数据处理能力和应用意识.复习备考时,要把基础知识理解透彻,在情境问题中能够发现考查的本质问题.
(1)注重情境,注重审题
考查概率、统计的试题多以生产生活中的实际问题为背景,阅读量大,首先根据文字信息、图表信息了解考查的知识点,再结合考查目标,理解图文的内在含义,最后整合有效信息,明确数据关系.对题目的准确理解,找到数学模型是解答题目的关键.
(2)关注素材,注重图表
图表语言具有直观、简洁、信息量大等特点,高考试题经常以图表作为情境材料呈现,准确读表(图)、识表(图)和用表(图)的能力至关重要,要从图表中获取有效信息,灵活运用图表信息作出统计推断和决策.
(3)关注生活,注重应用
多关注生活背景、社会现实、经济建设、科技发展、体育精神等各个方面,培养和提升数据处理能力、数学建模能力,培养用数据说话的理性思维.
(4)重视交汇,提升能力
统计与概率具有广泛应用性,一方面,统计和概率、计数原理等知识可以有机结合,即以统计知识为背景,以频率来估计概率或计数为基础,过渡到概率问题;另一方面,统计与概率可以和其他数学知识相结合,如可以和函数、数列、不等式等结合.因此在复习备考中,有必要针对统计与概率和其他知识相结合的问题进行训练.
题型一 概率中递推关系的应用——马尔科夫链
马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是…,Xt-2,Xt-1,Xt,Xt+1,…,那么Xt+1时刻的状态的条件概率仅依赖前一状态Xt,即P(Xt+1|…,Xt-2,Xt-1,Xt)=P(Xt+1|Xt).
[典例1] (2024·无锡江阴期初)王先生准备每天从骑自行车和开车两种出行方式中随机选择一种出行.从即日起出行方式选择规则自定如下:第一天选择骑自行车出行,随后每天用“一次性抛掷4枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于3,则该天出行方式与前一天相同,否则选择另一种出行方式.设pn(n∈N*)表示事件“第n天王先生选择骑自行车出行”的概率.
(1)用pn-1表示pn(n≥2);
(2)求pn(n≥2).
[解] (1)设一次性抛掷4枚均匀硬币得到正面向上的枚数为ξ,则ξ~
B,P(ξ<3)==,则P(ξ≥3)=1-P(ξ<3)=.用An-1表示事件“第(n-1)天王先生选择
的是骑自行车出行”,An表示事件“第n天王先生选择的是骑自行车出行”,由全概率公式知:pn=P(An)=
=pn-1·P(ξ<3)+(1-pn-1)·P(ξ≥3)=pn-1+(1-pn-1)=pn-1+,所以pn=pn-1+(n≥2).
(2)由(1)知,pn-=,n≥2,因为p1=1,所以p1-=,所以pn-≠0,所以=,所以数列是首项为,公比为的等比数列,从而pn-=,于是pn=+.
反思领悟 概率中的数列问题解题步骤
(1)弄清初始事件的概率p1(或p0).
(2)利用事件关系寻求第n步的概率pn与第(n+1)步的概率pn+1之间的关系,即递推关系pn+1=f (pn).
(3)利用数列的相关知识,由已知p1与pn+1=f (pn)求出通项公式pn.
【教用·备选题】
为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=
P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
①证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
②求p4,并根据p4的值解释这种试验方案的合理性.
[解] (1)X的所有可能取值为-1,0,1.
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β).
所以X的分布列为
X -1 0 1
P (1-α)β αβ+(1-α)(1-β) α(1-β)
(2)①证明:由(1)得a=0.4,b=0.5,c=0.1.
因此pi=0.4pi-1+0.5pi+0.1pi+1,故0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=.
又因为p1-p0=p1≠0,所以{pi+1-pi}(i=0,1,2,…,7)为公比为4,首项为p1的等比数列.
②由①可得
p8=p8-p7+p7-p6+…+p1-p0+p0
=(p8-p7)+(p7-p6)+…+(p1-p0)=p1.
由于p8=1,故p1=,
所以p4=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)
=p1=.
p4表示最终认为甲药更有效的概率.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为p4=
≈0.003 9,此时得出错误结论的概率非常小,说明这种试验方案
合理.
题型二 以统计图表为载体的概率统计问题
[典例2] 为了解某高校学生每天的运动时间,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天平均运动时间(单位:分钟)的频率分布直方图,将每天平均运动时间不低于40分钟的学生称为“运动族”.
(1)用样本估计总体,已知某学生每天平均运动时间不低于20分钟,求该学生是“运动族”的概率;
(2)从样本里的“运动族”学生中随机选取两位
同学,用随机变量X表示每天平均运动时间在
40~50分钟之间的学生数,求X的分布列及期望.
[解] (1)由频率分布直方图可知,
10×(0.01+0.018+0.022+0.025+0.020+a)=1,
解得a=0.005.
设“该学生每天平均运动时间不低于20分钟”为事件A,“该学生是‘运动族’”为事件B,
则P(A)=0.72,P(AB)=0.25,
所以在该学生每天平均运动时间不低于20分钟的条件下是“运动
族”的概率为P(B|A)===.
(2)由题意可知,样本中共有“运动族”学生25人,运动时间在40~50分钟之间的学生有20人,
所以X=0,1,2.
P(X=0)==,P(X=1)==,P(X=2)==,
X的分布列为
X 0 1 2
P
E(X)=0×+1×+2×=.
反思领悟 高考题常将频率分布直方图与概率、统计等交汇在一起进行考查,解题时要正确理解频率分布直方图,能利用频率分布直方图正确计算出各组数据,概率问题以计算为主,往往和实际问题相结合,要注意理解实际问题的意义,使之和相应的概率计算对应起来.
题型三 概率、统计与函数的交汇问题
[典例3] 根据以往大量的测量知某加工厂生产的钢管内径尺寸X(单位:mm)服从正态分布N(μ,σ2),并把钢管内径在[μ-σ,μ+σ]内的产品称为一等品,钢管内径在[μ+σ,μ+2σ]内的产品称为二等品,一等品与二等品统称为正品,其余范围内的产品作为废品回收.现从该企业生产的产品中随机抽取1 000件,测得钢管内径的样本数据的频率分布直方图如图.
(1)通过检测得样本数据的标准差s=0.3,用样本平均数x作为μ的近似值,用样本标准差s作为σ的估计值,根据所给数据求该企业生产的产品为正品的概率P1;(同一组中的数据用该区间的中点值代表)
(2)假如企业包装时要求把2个一等品和n(n≥2,n∈N)个二等品装在同一个箱子中,质检员从某箱子中摸出两件产品进行检验,若抽取到的两件产品等级相同,则该箱产品记为A,否则该箱产品记为B.
①试用含n的代数式表示某箱产品抽检被记为B的概率p;
②设抽检5箱产品恰有3箱被记为B的概率为f (p),求当n为何值时,f (p)取得最大值,并求出最大值.
参考数据:36.2×0.2+36.4×0.25+36.6×0.7+36.8×0.8+37×1.1+37.2×0.8+37.4×0.65+37.6×0.4+37.8×0.1≈185.
[解] (1)由题意,估计从该企业生产的产品中随机抽取1 000件钢管内径的平均数为≈185×0.2=37,
所以μ=37,σ=s=0.3,
则μ-σ=37-0.3=36.7,μ+σ=37+0.3=37.3,μ+2σ=37+0.6=37.6,
则一等品内径在[μ-σ,μ+σ]内,即在[36.7,37.3]内,
二等品内径在[μ+σ,μ+2σ]内,即在[37.3,37.6]内,
所以该企业生产的产品为正品的概率P1=P(36.7≤X≤37.6)=(0.8+1.1+0.8+0.65)×0.2+0.4×0.1=0.71.
(2)①从n+2件正品中任选2个,有种选法,其中等级相同的有种选法,
所以某箱产品抽检被记为B的概率为p==1-=.
②由题意,一箱产品抽检被记为B的概率为p,
则5箱产品恰有3箱被记为B的概率为f (p)=p3(1-p)2=10p3(1-2p+p2)=10(p3-2p4+p5),
f ′(p)=10(3p2-8p3+5p4)=10p2(3-8p+5p2)=10p2(p-1)(5p-3),
所以当p∈时,f ′(p)>0,函数f (p)单调递增,当p∈
时,f ′(p)<0,函数f (p)单调递减,
所以当p=时,f (p)取得最大值为f ==,此时,p==,
解得n=3或n=(舍去),
所以当n=3时,f (p)取得最大值.
反思领悟 通过设置变量,利用数学期望、方差或概率的计算公式构造函数,是概率与函数问题结合最常用的方式.解决此类问题,应注意两个问题:
(1)准确构造函数,利用公式搭建函数模型时,由于随机变量的数学期望、方差,随机事件概率的计算中涉及变量较多,式子较为复杂,所以准确运算化简是关键;
(2)注意变量的取值范围,一是题中给出的范围,二是实际问题中变量自身取值的限制.
【教用·备选题】
已知某工厂加工5G手机的某种精密配件的合格率为p(0(1)求p0;
(2)设该工厂加工5G手机的这种精密配件的合格率为p0,在合格品中,优等品的概率为0.5.
①从加工后的这种精密配件中随机抽取若干件,设其中优等品有X件,若P(X=6)最大,求抽取的这种精密配件最多有多少件;
②已知某5G手机生产商向该工厂提供这种精密配件的原料,经过该工厂加工后,每件优等品、合格品分别以150元、100元被该5G手机生产商回收,同时该工厂对不合格品进行复修,每件不合格品只能复修为合格品或不合格品,且复修为合格品和不合格品的概率均为0.5,复修后的合格品按合格品的价格被回收,复修后的不合格品按废品处理掉,且每件不合格品还需要向该5G手机生产商赔偿原料费30元.若该工厂要求每个这种精密配件至少获利50元,加工费与复修费相等,求一个这种精密配件的加工费最高为多少元?
[解] (1)由题意可知,这种精密配件的不合格率为1-p,则加工后的30件这种精密配件中恰有6件不合格的概率f (p)=(1-p)6p24(0则f ′(p)=(1-p)6p23=(1-p)5p23(4-5p),
令f ′(p)>0,解得0所以f (p)在(0,0.8)上单调递增,在(0.8,1)上单调递减,
所以当p=0.8时,f (p)取得极大值,故p0=0.8.
(2)①从加工后的这种精密配件中随机抽取一件为优等品的概率为0.8×0.5=0.4.
设从加工后的这种精密配件中随机抽取n件,由题意可知,X~B(n,0.4),且P(X=k)=0.4k×(1-0.4)n-k,
由题意可知,
即
解得14≤n≤16.5,又n∈N,所以n的最大值为16,
故抽取的这种精密配件最多有16件.
②设该工厂加工一个这种精密配件获利Y元,加工费与复修费均为m元,由题意可知,Y的可能取值为150-m,100-m,100-2m,
-30-2m,
则随机变量Y的分布列为
Y 150-m 100-m 100-2m -30-2m
P 0.4 0.4 0.1 0.1
则E(Y)=0.4(150-m)+0.4(100-m)+0.1(100-2m)+0.1(-30-2m)=107-1.2m,由题意可知,107-1.2m≥50,
解得m≤47.5,所以一个配件的加工费最高为47.5元.
进阶训练(十五) 概率、统计的交汇问题
1.某企业从生产的一批零件中抽取100件产品作为样本,检测其质量指标值m(m∈[100,400]),得到如图所示的频率分布直方图,并依据质量指标值划分等级如下表所示:
题号
1
3
5
2
4
6
8
7
9
10
11
12
质量指 标值m 150≤m<350 100≤m<150或
350≤m≤400
等级 A级 B级
题号
1
3
2
4
(1)根据频率分布直方图估计这100件产品的质量指标值的平均数;
(2)以样本的频率估计总体的概率,解决下列问题:
①从所生产的零件中随机抽取3个零件,记其中A级零件的件数为ξ,求ξ的分布列和数学期望;
②该企业采用混装的方式将所有零件按400个为一箱包装出售,已知一个A级零件的利润是12元,一个B级零件的利润是4元,估计每箱零件的利润.
题号
1
3
2
4
[解] (1)由题意知=125×0.05+175×0.1+225×0.15+275×0.4+325×0.25+375×0.05=267.5.
(2)①由题意知随机抽取一个零件,其为A级的概率为1-0.05×2=0.9,ξ的所有可能取值为0,1,2,3,
P(ξ=0)=(1-0.9)3=0.001,
P(ξ=1)=×0.9×(1-0.9)2=0.027,
P(ξ=2)=×0.92×(1-0.9)=0.243,
P(ξ=3)=×0.93=0.729,
题号
1
3
2
4
则随机变量ξ的分布列为
ξ 0 1 2 3
P 0.001 0.027 0.243 0.729
法一:所以E(ξ)=0×0.001+1×0.027+2×0.243+3×0.729=2.7.
法二:因为ξ~B(3,0.9),所以E(ξ)=3×0.9=2.7.
②设随机抽取一箱零件,其中A级零件有X个,则B级零件有(400-X)个,出售该箱零件的利润为Y元,Y=12X+4(400-X)=8X+1 600,因为X~B(400,0.9),所以E(X)=400×0.9=360,
所以E(Y)=E(8X+1 600)=8E(X)+1 600=8×360+1 600=4 480.
题号
1
3
2
4
2.(2024·广东佛山一模)佛山岭南天地位于禅城区祖庙大街2号,主要景点有龙塘诗社、文会里嫁娶屋、南风古灶、李众胜堂祖铺、祖庙大街等,这里的每一处景色都极具岭南特色,其中龙塘诗社和祖庙大街很受年轻人的青睐.为进一步合理配置旅游资源,现对已在龙塘诗社游览的游客进行随机问卷调查,若继续游玩祖庙大街景点的记2分,若不继续游玩祖庙大街景点的记1分,
每位游客选择是否游览祖庙大街的概率均为,游客之间的选择意
愿相互独立.
题号
1
3
2
4
(1)从游客中随机抽取3人,记总得分为X,求X的分布列与数学期望;
(2)①若从游客中随机抽取m人,记总得分恰为m分的概率为Am,求数列的前10项和;
②在对所有游客进行随机问卷调查过程中,记已调查过的累计得分恰为n分的概率为Bn,探讨Bn与Bn-1之间的关系式,并求数列的通项公式.
题号
1
3
2
4
[解] (1)X的可能取值为3,4,5,6.
P(X=3)==,P(X=4)==,
P(X=5)==,P(X=6)==.
所以X的分布列为
X 3 4 5 6
P
则E(X)=3×+4×+5×+6×=.
题号
1
3
2
4
(2)①总分恰为m的概率Am=,
所以数列{Am}是首项为,公比为的等比数列,
所以前10项和为S10==1-=.
②已调查的累计得分恰为n分的概率为Bn,
而得不到n分的情况只有先得到(n-1)分,再得2分,
概率为Bn-1,其中B1=,
所以1-Bn=Bn-1,Bn=-Bn-1+1,
题号
1
3
2
4
所以Bn-=-,又=-≠0,
即是等比数列,公比为-,首项为-.
所以Bn-=-,
即Bn==.
题号
1
3
2
4
3.乒乓球被称为我国的“国球”,是一种深受人们喜爱的球类体育项目.在某高校运动会的女子乒乓球单打半决赛阶段,规定:每场比赛采用七局四胜制,率先取得四局比赛胜利的选手获胜,且该场比赛结束.已知甲、乙两名运动员进行了一场比赛,且均充分发挥出了水平,其中甲运动员每局比赛获胜的概率为p(0(1)若前三局比赛中,甲至少赢得一局比赛的概率为p,求乙每局比赛获胜的概率;
(2)若前三局比赛中甲只赢了一局,设这场比赛结束还需要比赛的局数为ξ,求ξ的分布列和数学期望E(ξ),并求当p为何值时,E(ξ)最大.
题号
1
3
2
4
[解] (1)设事件A为“前三局比赛中,甲至少赢得一局比赛”,
则P(A)=1-(1-p)3=p,化简得25p2-75p+36=0,即(5p-3)(5p-12)=0,
所以p=或p=(舍去),所以乙每局比赛获胜的概率为1-p=.
题号
1
3
2
4
(2)由题意知,ξ的所有可能取值为2,3,4,且P(ξ=2)=(1-p)2=1-2p+p2,
P(ξ=3)=p(1-p)2=3p3-4p2+2p,
P(ξ=4)=p2(1-p)×1=3p2-3p3.
则ξ的分布列为
ξ 2 3 4
P 1-2p+p2 3p3-4p2+2p 3p2-3p3
题号
1
3
2
4
所以E(ξ)=-3p3)=
-3p3+2p2+2p+2(02(0当p∈时,f ′(p)>0,f (p)单调递增;
当p∈时,f ′(p)<0,f (p)单调递减.
所以当且仅当p=时,f (p)最大,即当p=时,E(ξ)最大.
题号
1
3
2
4
4.某高中学校为了解学生参加体育锻炼的情况,统计了全校所有学生在一年内每周参加体育锻炼的次数,现随机抽取了60名同学(其中男生30名,女生30名)在某一周参加体育锻炼的数据,结果如下表:
一周参加体育锻炼的次数 0 1 2 3 4 5 6 7
男生人数 1 2 4 5 6 5 4 3
女生人数 4 5 5 6 4 3 2 1
合计 5 7 9 11 10 8 6 4
题号
1
3
2
4
(1)若将一周参加体育锻炼次数为3次及3次以上的称为“经常锻炼”,其余的称为“不经常锻炼”,请完成以下2×2列联表,并依据小概率值α=0.1的独立性检验,判断能否认为学生体育锻炼的经常性与性别有关系;
单位:人
性别 体育锻炼 合计
不经常 经常
男生
女生
合计
题号
1
3
2
4
(2)若将一周参加体育锻炼的次数为0次的称为“极度缺乏锻炼”,“极度缺乏锻炼”会导致肥胖等诸多健康问题.以样本频率估计概率,在全校抽取20名同学,其中“极度缺乏锻炼”的人数为X,求E(X)和D(X);
题号
1
3
2
4
(3)若将一周参加体育锻炼的次数为6次或7次的同学称为“运动爱好者”,为进一步了解他们的生活习惯,在样本的10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附:χ2=,n=a+b+c+d.
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
题号
1
3
2
4
[解] (1)完成列联表如下.
单位:人
性别 体育锻炼 合计
不经常 经常
男生 7 23 30
女生 14 16 30
合计 21 39 60
题号
1
3
2
4
零假设为
H0:学生体育锻炼的经常性与性别无关.
根据列联表中的数据计算,得
χ2=≈3.590>2.706=x0.1.
依据小概率值α=0.1的独立性检验,推断H0不成立,即学生体育锻炼的经常性与性别有关系,此推断犯错误的概率不超过0.1.
题号
1
3
2
4
(2)因为学校总的学生人数远大于所抽取的学生人数,故X近似服从二项分布,随机抽取1名学生为“极度缺乏锻炼”者的概率P=
=,则X~B,
故E(X)=20×=,
D(X)=20×=.
题号
1
3
2
4
(3)由题意可知,10名“运动爱好者”中有7名男生,3名女生,则Y的可能取值为0,1,2,3,
则P(Y=0)==,P(Y=1)===,
P(Y=2)===,P(Y=3)===,
故所求分布列为
Y 0 1 2 3
P
E(Y)=0×+1×+2×+3×=2.1.
题号
1
3
2
4
谢 谢 !
第十章 统计与成对数据的统计分析
思维进阶15 概率、统计的交汇问题
近几年高考特别注重对概率和统计结合、概率和其他知识(如数列与函数)结合的综合考查,通常以实际问题为背景,通过构建数学模型,突出考查统计与概率思想、数据处理能力和应用意识.复习备考时,要把基础知识理解透彻,在情境问题中能够发现考查的本质问题.
(1)注重情境,注重审题
考查概率、统计的试题多以生产生活中的实际问题为背景,阅读量大,首先根据文字信息、图表信息了解考查的知识点,再结合考查目标,理解图文的内在含义,最后整合有效信息,明确数据关系.对题目的准确理解,找到数学模型是解答题目的关键.
(2)关注素材,注重图表
图表语言具有直观、简洁、信息量大等特点,高考试题经常以图表作为情境材料呈现,准确读表(图)、识表(图)和用表(图)的能力至关重要,要从图表中获取有效信息,灵活运用图表信息作出统计推断和决策.
(3)关注生活,注重应用
多关注生活背景、社会现实、经济建设、科技发展、体育精神等各个方面,培养和提升数据处理能力、数学建模能力,培养用数据说话的理性思维.
(4)重视交汇,提升能力
统计与概率具有广泛应用性,一方面,统计和概率、计数原理等知识可以有机结合,即以统计知识为背景,以频率来估计概率或计数为基础,过渡到概率问题;另一方面,统计与概率可以和其他数学知识相结合,如可以和函数、数列、不等式等结合.因此在复习备考中,有必要针对统计与概率和其他知识相结合的问题进行训练.
题型一 概率中递推关系的应用——马尔科夫链
马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是…,Xt-2,Xt-1,Xt,Xt+1,…,那么Xt+1时刻的状态的条件概率仅依赖前一状态Xt,即P(Xt+1|…,Xt-2,Xt-1,Xt)=P(Xt+1|Xt).
[典例1] (2024·无锡江阴期初)王先生准备每天从骑自行车和开车两种出行方式中随机选择一种出行.从即日起出行方式选择规则自定如下:第一天选择骑自行车出行,随后每天用“一次性抛掷4枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于3,则该天出行方式与前一天相同,否则选择另一种出行方式.设pn(n∈N*)表示事件“第n天王先生选择骑自行车出行”的概率.
(1)用pn-1表示pn(n≥2);
(2)求pn(n≥2).
[解] (1)设一次性抛掷4枚均匀硬币得到正面向上的枚数为ξ,则ξ~
B,P(ξ<3)==,则P(ξ≥3)=1-P(ξ<3)=.用An-1表示事件“第(n-1)天王先生选择
的是骑自行车出行”,An表示事件“第n天王先生选择的是骑自行车出行”,由全概率公式知:pn=P(An)=
=pn-1·P(ξ<3)+(1-pn-1)·P(ξ≥3)=pn-1+(1-pn-1)=pn-1+,所以pn=pn-1+(n≥2).
(2)由(1)知,pn-=,n≥2,因为p1=1,所以p1-=,所以pn-≠0,所以=,所以数列是首项为,公比为的等比数列,从而pn-=,于是pn=+.
反思领悟 概率中的数列问题解题步骤
(1)弄清初始事件的概率p1(或p0).
(2)利用事件关系寻求第n步的概率pn与第(n+1)步的概率pn+1之间的关系,即递推关系pn+1=f (pn).
(3)利用数列的相关知识,由已知p1与pn+1=f (pn)求出通项公式pn.
【教用·备选题】
为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=
P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
①证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
②求p4,并根据p4的值解释这种试验方案的合理性.
[解] (1)X的所有可能取值为-1,0,1.
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β).
所以X的分布列为
X -1 0 1
P (1-α)β αβ+(1-α)(1-β) α(1-β)
(2)①证明:由(1)得a=0.4,b=0.5,c=0.1.
因此pi=0.4pi-1+0.5pi+0.1pi+1,故0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=.
又因为p1-p0=p1≠0,所以{pi+1-pi}(i=0,1,2,…,7)为公比为4,首项为p1的等比数列.
②由①可得
p8=p8-p7+p7-p6+…+p1-p0+p0
=(p8-p7)+(p7-p6)+…+(p1-p0)=p1.
由于p8=1,故p1=,
所以p4=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)
=p1=.
p4表示最终认为甲药更有效的概率.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为p4=
≈0.003 9,此时得出错误结论的概率非常小,说明这种试验方案
合理.
题型二 以统计图表为载体的概率统计问题
[典例2] 为了解某高校学生每天的运动时间,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天平均运动时间(单位:分钟)的频率分布直方图,将每天平均运动时间不低于40分钟的学生称为“运动族”.
(1)用样本估计总体,已知某学生每天平均运动时间不低于20分钟,求该学生是“运动族”的概率;
(2)从样本里的“运动族”学生中随机选取两位
同学,用随机变量X表示每天平均运动时间在
40~50分钟之间的学生数,求X的分布列及期望.
[解] (1)由频率分布直方图可知,
10×(0.01+0.018+0.022+0.025+0.020+a)=1,
解得a=0.005.
设“该学生每天平均运动时间不低于20分钟”为事件A,“该学生是‘运动族’”为事件B,
则P(A)=0.72,P(AB)=0.25,
所以在该学生每天平均运动时间不低于20分钟的条件下是“运动
族”的概率为P(B|A)===.
(2)由题意可知,样本中共有“运动族”学生25人,运动时间在40~50分钟之间的学生有20人,
所以X=0,1,2.
P(X=0)==,P(X=1)==,P(X=2)==,
X的分布列为
X 0 1 2
P
E(X)=0×+1×+2×=.
反思领悟 高考题常将频率分布直方图与概率、统计等交汇在一起进行考查,解题时要正确理解频率分布直方图,能利用频率分布直方图正确计算出各组数据,概率问题以计算为主,往往和实际问题相结合,要注意理解实际问题的意义,使之和相应的概率计算对应起来.
题型三 概率、统计与函数的交汇问题
[典例3] 根据以往大量的测量知某加工厂生产的钢管内径尺寸X(单位:mm)服从正态分布N(μ,σ2),并把钢管内径在[μ-σ,μ+σ]内的产品称为一等品,钢管内径在[μ+σ,μ+2σ]内的产品称为二等品,一等品与二等品统称为正品,其余范围内的产品作为废品回收.现从该企业生产的产品中随机抽取1 000件,测得钢管内径的样本数据的频率分布直方图如图.
(1)通过检测得样本数据的标准差s=0.3,用样本平均数x作为μ的近似值,用样本标准差s作为σ的估计值,根据所给数据求该企业生产的产品为正品的概率P1;(同一组中的数据用该区间的中点值代表)
(2)假如企业包装时要求把2个一等品和n(n≥2,n∈N)个二等品装在同一个箱子中,质检员从某箱子中摸出两件产品进行检验,若抽取到的两件产品等级相同,则该箱产品记为A,否则该箱产品记为B.
①试用含n的代数式表示某箱产品抽检被记为B的概率p;
②设抽检5箱产品恰有3箱被记为B的概率为f (p),求当n为何值时,f (p)取得最大值,并求出最大值.
参考数据:36.2×0.2+36.4×0.25+36.6×0.7+36.8×0.8+37×1.1+37.2×0.8+37.4×0.65+37.6×0.4+37.8×0.1≈185.
[解] (1)由题意,估计从该企业生产的产品中随机抽取1 000件钢管内径的平均数为≈185×0.2=37,
所以μ=37,σ=s=0.3,
则μ-σ=37-0.3=36.7,μ+σ=37+0.3=37.3,μ+2σ=37+0.6=37.6,
则一等品内径在[μ-σ,μ+σ]内,即在[36.7,37.3]内,
二等品内径在[μ+σ,μ+2σ]内,即在[37.3,37.6]内,
所以该企业生产的产品为正品的概率P1=P(36.7≤X≤37.6)=(0.8+1.1+0.8+0.65)×0.2+0.4×0.1=0.71.
(2)①从n+2件正品中任选2个,有种选法,其中等级相同的有种选法,
所以某箱产品抽检被记为B的概率为p==1-=.
②由题意,一箱产品抽检被记为B的概率为p,
则5箱产品恰有3箱被记为B的概率为f (p)=p3(1-p)2=10p3(1-2p+p2)=10(p3-2p4+p5),
f ′(p)=10(3p2-8p3+5p4)=10p2(3-8p+5p2)=10p2(p-1)(5p-3),
所以当p∈时,f ′(p)>0,函数f (p)单调递增,当p∈
时,f ′(p)<0,函数f (p)单调递减,
所以当p=时,f (p)取得最大值为f ==,此时,p==,
解得n=3或n=(舍去),
所以当n=3时,f (p)取得最大值.
反思领悟 通过设置变量,利用数学期望、方差或概率的计算公式构造函数,是概率与函数问题结合最常用的方式.解决此类问题,应注意两个问题:
(1)准确构造函数,利用公式搭建函数模型时,由于随机变量的数学期望、方差,随机事件概率的计算中涉及变量较多,式子较为复杂,所以准确运算化简是关键;
(2)注意变量的取值范围,一是题中给出的范围,二是实际问题中变量自身取值的限制.
【教用·备选题】
已知某工厂加工5G手机的某种精密配件的合格率为p(0
(2)设该工厂加工5G手机的这种精密配件的合格率为p0,在合格品中,优等品的概率为0.5.
①从加工后的这种精密配件中随机抽取若干件,设其中优等品有X件,若P(X=6)最大,求抽取的这种精密配件最多有多少件;
②已知某5G手机生产商向该工厂提供这种精密配件的原料,经过该工厂加工后,每件优等品、合格品分别以150元、100元被该5G手机生产商回收,同时该工厂对不合格品进行复修,每件不合格品只能复修为合格品或不合格品,且复修为合格品和不合格品的概率均为0.5,复修后的合格品按合格品的价格被回收,复修后的不合格品按废品处理掉,且每件不合格品还需要向该5G手机生产商赔偿原料费30元.若该工厂要求每个这种精密配件至少获利50元,加工费与复修费相等,求一个这种精密配件的加工费最高为多少元?
[解] (1)由题意可知,这种精密配件的不合格率为1-p,则加工后的30件这种精密配件中恰有6件不合格的概率f (p)=(1-p)6p24(0
令f ′(p)>0,解得0
所以当p=0.8时,f (p)取得极大值,故p0=0.8.
(2)①从加工后的这种精密配件中随机抽取一件为优等品的概率为0.8×0.5=0.4.
设从加工后的这种精密配件中随机抽取n件,由题意可知,X~B(n,0.4),且P(X=k)=0.4k×(1-0.4)n-k,
由题意可知,
即
解得14≤n≤16.5,又n∈N,所以n的最大值为16,
故抽取的这种精密配件最多有16件.
②设该工厂加工一个这种精密配件获利Y元,加工费与复修费均为m元,由题意可知,Y的可能取值为150-m,100-m,100-2m,
-30-2m,
则随机变量Y的分布列为
Y 150-m 100-m 100-2m -30-2m
P 0.4 0.4 0.1 0.1
则E(Y)=0.4(150-m)+0.4(100-m)+0.1(100-2m)+0.1(-30-2m)=107-1.2m,由题意可知,107-1.2m≥50,
解得m≤47.5,所以一个配件的加工费最高为47.5元.
进阶训练(十五) 概率、统计的交汇问题
1.某企业从生产的一批零件中抽取100件产品作为样本,检测其质量指标值m(m∈[100,400]),得到如图所示的频率分布直方图,并依据质量指标值划分等级如下表所示:
题号
1
3
5
2
4
6
8
7
9
10
11
12
质量指 标值m 150≤m<350 100≤m<150或
350≤m≤400
等级 A级 B级
题号
1
3
2
4
(1)根据频率分布直方图估计这100件产品的质量指标值的平均数;
(2)以样本的频率估计总体的概率,解决下列问题:
①从所生产的零件中随机抽取3个零件,记其中A级零件的件数为ξ,求ξ的分布列和数学期望;
②该企业采用混装的方式将所有零件按400个为一箱包装出售,已知一个A级零件的利润是12元,一个B级零件的利润是4元,估计每箱零件的利润.
题号
1
3
2
4
[解] (1)由题意知=125×0.05+175×0.1+225×0.15+275×0.4+325×0.25+375×0.05=267.5.
(2)①由题意知随机抽取一个零件,其为A级的概率为1-0.05×2=0.9,ξ的所有可能取值为0,1,2,3,
P(ξ=0)=(1-0.9)3=0.001,
P(ξ=1)=×0.9×(1-0.9)2=0.027,
P(ξ=2)=×0.92×(1-0.9)=0.243,
P(ξ=3)=×0.93=0.729,
题号
1
3
2
4
则随机变量ξ的分布列为
ξ 0 1 2 3
P 0.001 0.027 0.243 0.729
法一:所以E(ξ)=0×0.001+1×0.027+2×0.243+3×0.729=2.7.
法二:因为ξ~B(3,0.9),所以E(ξ)=3×0.9=2.7.
②设随机抽取一箱零件,其中A级零件有X个,则B级零件有(400-X)个,出售该箱零件的利润为Y元,Y=12X+4(400-X)=8X+1 600,因为X~B(400,0.9),所以E(X)=400×0.9=360,
所以E(Y)=E(8X+1 600)=8E(X)+1 600=8×360+1 600=4 480.
题号
1
3
2
4
2.(2024·广东佛山一模)佛山岭南天地位于禅城区祖庙大街2号,主要景点有龙塘诗社、文会里嫁娶屋、南风古灶、李众胜堂祖铺、祖庙大街等,这里的每一处景色都极具岭南特色,其中龙塘诗社和祖庙大街很受年轻人的青睐.为进一步合理配置旅游资源,现对已在龙塘诗社游览的游客进行随机问卷调查,若继续游玩祖庙大街景点的记2分,若不继续游玩祖庙大街景点的记1分,
每位游客选择是否游览祖庙大街的概率均为,游客之间的选择意
愿相互独立.
题号
1
3
2
4
(1)从游客中随机抽取3人,记总得分为X,求X的分布列与数学期望;
(2)①若从游客中随机抽取m人,记总得分恰为m分的概率为Am,求数列的前10项和;
②在对所有游客进行随机问卷调查过程中,记已调查过的累计得分恰为n分的概率为Bn,探讨Bn与Bn-1之间的关系式,并求数列的通项公式.
题号
1
3
2
4
[解] (1)X的可能取值为3,4,5,6.
P(X=3)==,P(X=4)==,
P(X=5)==,P(X=6)==.
所以X的分布列为
X 3 4 5 6
P
则E(X)=3×+4×+5×+6×=.
题号
1
3
2
4
(2)①总分恰为m的概率Am=,
所以数列{Am}是首项为,公比为的等比数列,
所以前10项和为S10==1-=.
②已调查的累计得分恰为n分的概率为Bn,
而得不到n分的情况只有先得到(n-1)分,再得2分,
概率为Bn-1,其中B1=,
所以1-Bn=Bn-1,Bn=-Bn-1+1,
题号
1
3
2
4
所以Bn-=-,又=-≠0,
即是等比数列,公比为-,首项为-.
所以Bn-=-,
即Bn==.
题号
1
3
2
4
3.乒乓球被称为我国的“国球”,是一种深受人们喜爱的球类体育项目.在某高校运动会的女子乒乓球单打半决赛阶段,规定:每场比赛采用七局四胜制,率先取得四局比赛胜利的选手获胜,且该场比赛结束.已知甲、乙两名运动员进行了一场比赛,且均充分发挥出了水平,其中甲运动员每局比赛获胜的概率为p(0
(2)若前三局比赛中甲只赢了一局,设这场比赛结束还需要比赛的局数为ξ,求ξ的分布列和数学期望E(ξ),并求当p为何值时,E(ξ)最大.
题号
1
3
2
4
[解] (1)设事件A为“前三局比赛中,甲至少赢得一局比赛”,
则P(A)=1-(1-p)3=p,化简得25p2-75p+36=0,即(5p-3)(5p-12)=0,
所以p=或p=(舍去),所以乙每局比赛获胜的概率为1-p=.
题号
1
3
2
4
(2)由题意知,ξ的所有可能取值为2,3,4,且P(ξ=2)=(1-p)2=1-2p+p2,
P(ξ=3)=p(1-p)2=3p3-4p2+2p,
P(ξ=4)=p2(1-p)×1=3p2-3p3.
则ξ的分布列为
ξ 2 3 4
P 1-2p+p2 3p3-4p2+2p 3p2-3p3
题号
1
3
2
4
所以E(ξ)=-3p3)=
-3p3+2p2+2p+2(0
当p∈时,f ′(p)<0,f (p)单调递减.
所以当且仅当p=时,f (p)最大,即当p=时,E(ξ)最大.
题号
1
3
2
4
4.某高中学校为了解学生参加体育锻炼的情况,统计了全校所有学生在一年内每周参加体育锻炼的次数,现随机抽取了60名同学(其中男生30名,女生30名)在某一周参加体育锻炼的数据,结果如下表:
一周参加体育锻炼的次数 0 1 2 3 4 5 6 7
男生人数 1 2 4 5 6 5 4 3
女生人数 4 5 5 6 4 3 2 1
合计 5 7 9 11 10 8 6 4
题号
1
3
2
4
(1)若将一周参加体育锻炼次数为3次及3次以上的称为“经常锻炼”,其余的称为“不经常锻炼”,请完成以下2×2列联表,并依据小概率值α=0.1的独立性检验,判断能否认为学生体育锻炼的经常性与性别有关系;
单位:人
性别 体育锻炼 合计
不经常 经常
男生
女生
合计
题号
1
3
2
4
(2)若将一周参加体育锻炼的次数为0次的称为“极度缺乏锻炼”,“极度缺乏锻炼”会导致肥胖等诸多健康问题.以样本频率估计概率,在全校抽取20名同学,其中“极度缺乏锻炼”的人数为X,求E(X)和D(X);
题号
1
3
2
4
(3)若将一周参加体育锻炼的次数为6次或7次的同学称为“运动爱好者”,为进一步了解他们的生活习惯,在样本的10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附:χ2=,n=a+b+c+d.
α 0.1 0.05 0.01
xα 2.706 3.841 6.635
题号
1
3
2
4
[解] (1)完成列联表如下.
单位:人
性别 体育锻炼 合计
不经常 经常
男生 7 23 30
女生 14 16 30
合计 21 39 60
题号
1
3
2
4
零假设为
H0:学生体育锻炼的经常性与性别无关.
根据列联表中的数据计算,得
χ2=≈3.590>2.706=x0.1.
依据小概率值α=0.1的独立性检验,推断H0不成立,即学生体育锻炼的经常性与性别有关系,此推断犯错误的概率不超过0.1.
题号
1
3
2
4
(2)因为学校总的学生人数远大于所抽取的学生人数,故X近似服从二项分布,随机抽取1名学生为“极度缺乏锻炼”者的概率P=
=,则X~B,
故E(X)=20×=,
D(X)=20×=.
题号
1
3
2
4
(3)由题意可知,10名“运动爱好者”中有7名男生,3名女生,则Y的可能取值为0,1,2,3,
则P(Y=0)==,P(Y=1)===,
P(Y=2)===,P(Y=3)===,
故所求分布列为
Y 0 1 2 3
P
E(Y)=0×+1×+2×+3×=2.1.
题号
1
3
2
4
谢 谢 !
同课章节目录
