《高考快车道》2026版高三一轮总复习数学(基础版)116 第十章 规范答题六 概率与统计的综合问题 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)116 第十章 规范答题六 概率与统计的综合问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:09 | ||
图片预览





文档简介
(共12张PPT)
第十章 统计与成对数据的统计分析
规范答题六 概率与统计的综合问题
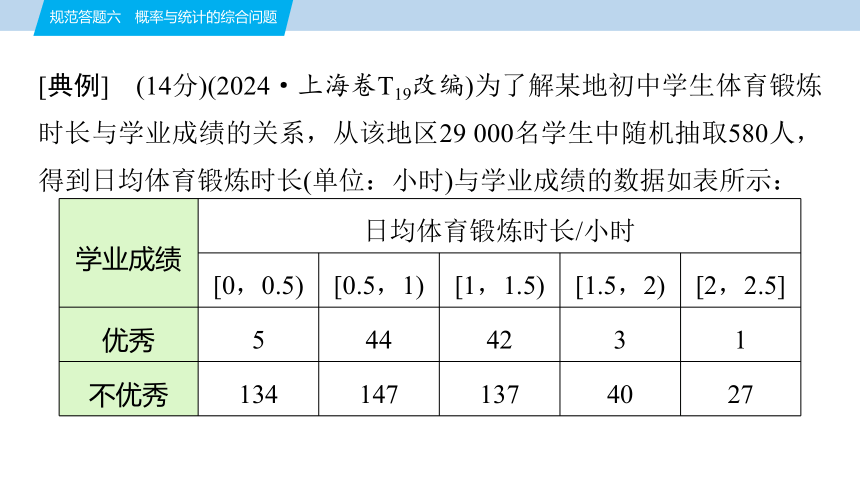
[典例] (14分)(2024·上海卷T19改编)为了解某地初中学生体育锻炼时长与学业成绩的关系,从该地区29 000名学生中随机抽取580人,得到日均体育锻炼时长(单位:小时)与学业成绩的数据如表所示:
学业成绩 日均体育锻炼时长/小时
[0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5]
优秀 5 44 42 3 1
不优秀 134 147 137 40 27
(1)该地区29 000名学生中日均体育锻炼时长不少于1小时的人数约为多少?
(2)估计该地区初中学生日均体育锻炼时长(精确到0.1小时).
(3)依据小概率值α=0.05的独立性检验,能否认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?
明条件,顺思路
①由信息“从该地区29 000名学生中随机抽取580人”想到总体中含
29 000个个体,580为样本容量.从统计表得到“日均体育锻炼时长不少于1小时的人包括两类:学业成绩优秀与不优秀,”故求出总和42+3+1+137+40+27=250.
②由数据信息,按比例抽样,求出相关占比即可.
③由“估计该地区初中学生日均体育锻炼时长”可得信息
(ⅰ)“估计”是通过抽取的580人的体育锻炼时长来计算;
(ⅱ)“日均”是求平均数.
明条件,顺思路
④由信息“为了解某地初中学生体育锻炼时长与学业成绩的关系”想到分类变量.
“学业成绩”分为“优秀和不优秀”,“体育锻炼时长”分为“时长不小于1小时且小于2小时与其他两类”,得出2×2列联表.
⑤由2×2列联表
(ⅰ)计算χ2值;
(ⅱ)和临界值比较大小得出结论.
规范答,抢得分
[解] (1)抽取的样本中日均体育锻炼时长不小于1小时的人数为42+3+1+137+40+27=250.
设该地区29 000名学生中有x人的日均体育锻炼时长不小于1小时,
则=,解得x=12 500.
故该地区29 000名学生中日均体育锻炼时长不少于1小时的人数约为12 500.……………………………………………………………(4分)
规范答,抢得分
(2)依题意得,该地区初中学生日均体育锻炼时长为(0.25×139+0.75×191+1.25×179+1.75×43+2.25×28)÷580=540÷580≈0.9.
所以该地区初中学生日均体育锻炼时长约为0.9小时.…………(8分)
规范答,抢得分
(3)对数据重新组合,得到2×2列联表
单位:人
学业成绩 日均体育锻炼时长/小时 合计
[1,2) 其他
优秀 45 50 95
不优秀 177 308 485
合计 222 358 580
规范答,抢得分
零假设为
H0:学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时无关.
χ2=≈3.976>3.841,
依据小概率值α=0.05的独立性检验,推出H0不成立,即认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关.(14分)
点关键,防陷阱
读懂信息,明确各数据的意义是正确解题的关键.
通过抽象概括得到样本与总体间的比例关系.
求平均数常见的两种类型:
①=(x1+x2+…+xn);
②等于各组区间的中点与相应频率之积的和.
点关键,防陷阱
2×2列联表中每一类变量都必须分为两类.
独立性检验步骤:
①抽取样本;
②列2×2列联表;
③提出零假设H0;
④求出χ2数值;
⑤根据χ2数值得出结论.
提醒:别忘写“零假设为H0”
谢 谢 !
第十章 统计与成对数据的统计分析
规范答题六 概率与统计的综合问题
[典例] (14分)(2024·上海卷T19改编)为了解某地初中学生体育锻炼时长与学业成绩的关系,从该地区29 000名学生中随机抽取580人,得到日均体育锻炼时长(单位:小时)与学业成绩的数据如表所示:
学业成绩 日均体育锻炼时长/小时
[0,0.5) [0.5,1) [1,1.5) [1.5,2) [2,2.5]
优秀 5 44 42 3 1
不优秀 134 147 137 40 27
(1)该地区29 000名学生中日均体育锻炼时长不少于1小时的人数约为多少?
(2)估计该地区初中学生日均体育锻炼时长(精确到0.1小时).
(3)依据小概率值α=0.05的独立性检验,能否认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关?
明条件,顺思路
①由信息“从该地区29 000名学生中随机抽取580人”想到总体中含
29 000个个体,580为样本容量.从统计表得到“日均体育锻炼时长不少于1小时的人包括两类:学业成绩优秀与不优秀,”故求出总和42+3+1+137+40+27=250.
②由数据信息,按比例抽样,求出相关占比即可.
③由“估计该地区初中学生日均体育锻炼时长”可得信息
(ⅰ)“估计”是通过抽取的580人的体育锻炼时长来计算;
(ⅱ)“日均”是求平均数.
明条件,顺思路
④由信息“为了解某地初中学生体育锻炼时长与学业成绩的关系”想到分类变量.
“学业成绩”分为“优秀和不优秀”,“体育锻炼时长”分为“时长不小于1小时且小于2小时与其他两类”,得出2×2列联表.
⑤由2×2列联表
(ⅰ)计算χ2值;
(ⅱ)和临界值比较大小得出结论.
规范答,抢得分
[解] (1)抽取的样本中日均体育锻炼时长不小于1小时的人数为42+3+1+137+40+27=250.
设该地区29 000名学生中有x人的日均体育锻炼时长不小于1小时,
则=,解得x=12 500.
故该地区29 000名学生中日均体育锻炼时长不少于1小时的人数约为12 500.……………………………………………………………(4分)
规范答,抢得分
(2)依题意得,该地区初中学生日均体育锻炼时长为(0.25×139+0.75×191+1.25×179+1.75×43+2.25×28)÷580=540÷580≈0.9.
所以该地区初中学生日均体育锻炼时长约为0.9小时.…………(8分)
规范答,抢得分
(3)对数据重新组合,得到2×2列联表
单位:人
学业成绩 日均体育锻炼时长/小时 合计
[1,2) 其他
优秀 45 50 95
不优秀 177 308 485
合计 222 358 580
规范答,抢得分
零假设为
H0:学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时无关.
χ2=≈3.976>3.841,
依据小概率值α=0.05的独立性检验,推出H0不成立,即认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关.(14分)
点关键,防陷阱
读懂信息,明确各数据的意义是正确解题的关键.
通过抽象概括得到样本与总体间的比例关系.
求平均数常见的两种类型:
①=(x1+x2+…+xn);
②等于各组区间的中点与相应频率之积的和.
点关键,防陷阱
2×2列联表中每一类变量都必须分为两类.
独立性检验步骤:
①抽取样本;
②列2×2列联表;
③提出零假设H0;
④求出χ2数值;
⑤根据χ2数值得出结论.
提醒:别忘写“零假设为H0”
谢 谢 !
同课章节目录
