《高考快车道》2026版高三一轮总复习数学(基础版)115 第十章 阶段提能(十八) 概率与统计 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)115 第十章 阶段提能(十八) 概率与统计 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:09 | ||
图片预览








文档简介
(共46张PPT)
第十章 统计与成对数据的统计分析
阶段提能(十八) 概率与统计
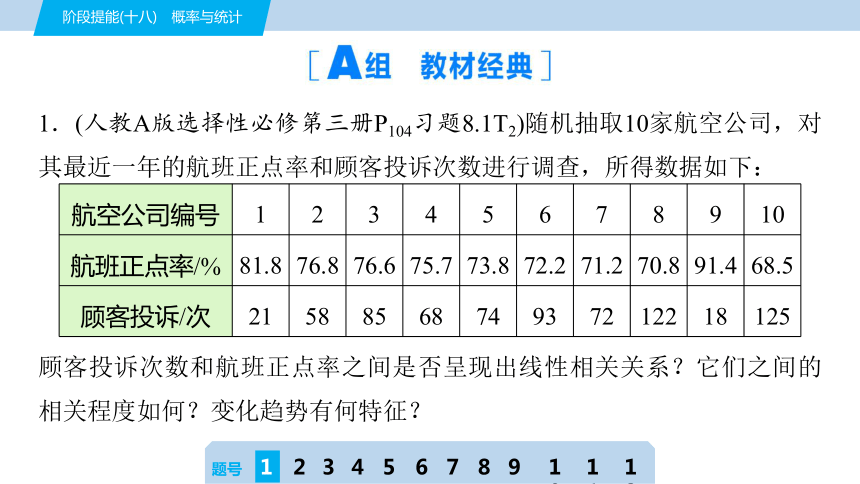
1.(人教A版选择性必修第三册P104习题8.1T2)随机抽取10家航空公司,对其最近一年的航班正点率和顾客投诉次数进行调查,所得数据如下:
题号
1
3
5
2
4
6
8
7
9
10
11
12
航空公司编号 1 2 3 4 5 6 7 8 9 10
航班正点率/% 81.8 76.8 76.6 75.7 73.8 72.2 71.2 70.8 91.4 68.5
顾客投诉/次 21 58 85 68 74 93 72 122 18 125
顾客投诉次数和航班正点率之间是否呈现出线性相关关系?它们之间的相关程度如何?变化趋势有何特征?
题号
1
3
5
2
4
6
8
7
9
10
11
12
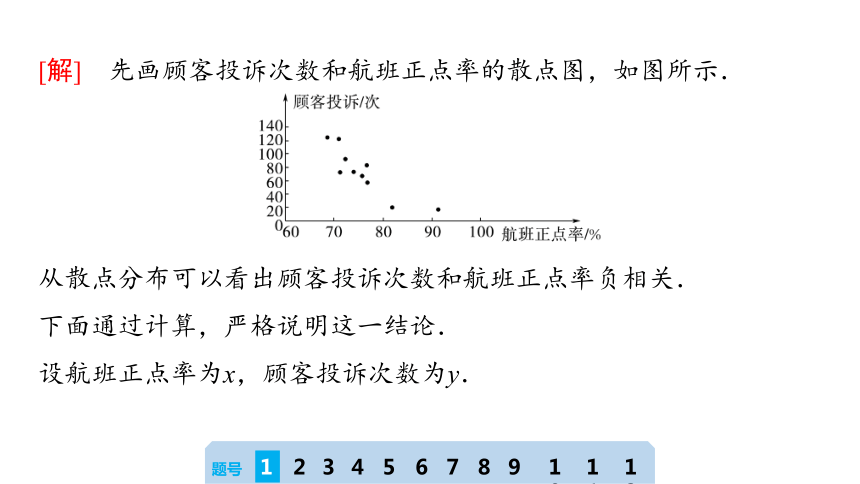
[解] 先画顾客投诉次数和航班正点率的散点图,如图所示.
从散点分布可以看出顾客投诉次数和航班正点率负相关.
下面通过计算,严格说明这一结论.
设航班正点率为x,顾客投诉次数为y.
由数据可得=73.6,=53 978.3,
=57 975.1,=65 796,
∴r==
≈-0.87.
由此可以推断,顾客投诉次数与航班正点率之间呈现出线性相关关系,相关程度较强,且为负相关,顾客投诉次数与航班正点率的变化趋势相反.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
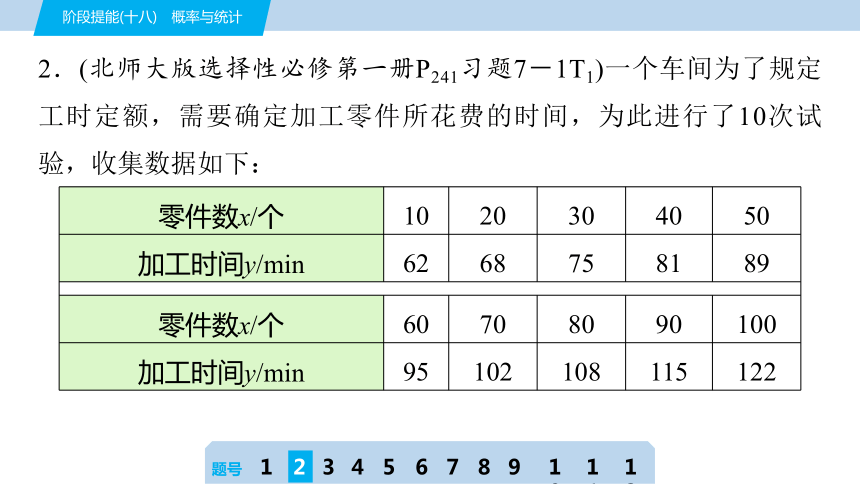
2.(北师大版选择性必修第一册P241习题7-1T1)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
零件数x/个 10 20 30 40 50
加工时间y/min 62 68 75 81 89
零件数x/个 60 70 80 90 100
加工时间y/min 95 102 108 115 122
(1)画出散点图;
(2)求y关于x的经验回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
[解] (1)散点图如下.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)由已知得=91.7,
)=5 515,
)2=8 250,所以=≈0.668,
≈91.7-0.668×55=54.96.
所以经验回归方程为=0.668x+54.96.
(3)关于加工零件的个数与加工时间,我们得到的结论是:加工的零件越多,所花的时间大致越长.
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教B版选择性必修第二册P122习题4-3BT4)某工厂有25周岁及以上的工人300名,25周岁以下的工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层随机抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁及以上”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下”的工人的概率;
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件列出2×2列联表,依据小概率值α=0.1的独立性检验,能否认为“生产能手”与工人所在的年龄组有关.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)由已知得样本中有25周岁及以上组工人60名,25周岁以下组工人40名,所以样本中日平均生产件数不足60件的工人中25周岁及以上组有60×0.05=3(人),分别记为A1,A2,A3,25周岁以下组有40×0.05=2(人),分别记为B1,B2,从中随机抽取2人,所有可能的结果共10种,分别是(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),其中至少抽到1名25周岁以下组的工
人的结果有7种,故所求概率P=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
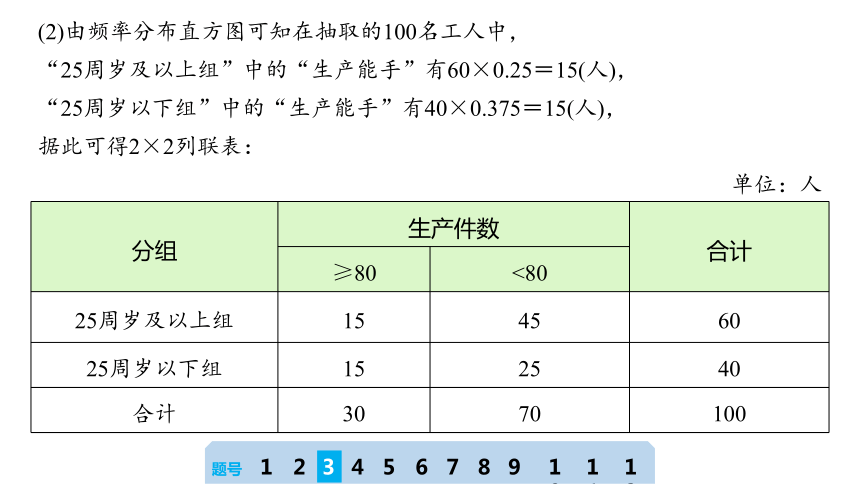
(2)由频率分布直方图可知在抽取的100名工人中,
“25周岁及以上组”中的“生产能手”有60×0.25=15(人),
“25周岁以下组”中的“生产能手”有40×0.375=15(人),
据此可得2×2列联表:
单位:人
分组 生产件数 合计
≥80 <80
25周岁及以上组 15 45 60
25周岁以下组 15 25 40
合计 30 70 100
题号
1
3
5
2
4
6
8
7
9
10
11
12
零假设为
H0:“生产能手”与工人所在的年龄组无关.
χ2==≈1.786<2.706.
所以依据小概率值α=0.1的独立性检验,没有充分证据推断H0不成立,即认为“生产能手”与工人所在的年龄组无关.
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教B版选择性必修第二册P128复习题C组T1)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:t)和年利润z(单位:万元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据进行了初步处理,得到下面的散点图及一些统计量的值.
表中wi==
·
46.6 563 6.8 289.8 1.6 1 469 108.8
题号
1
3
5
2
4
6
8
7
9
10
11
12
(1)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的经验回归方程类型?
(2)根据(1)的判断结果及表中数据,建立y关于x的经验回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:年宣传费x=49时,年销售量及年利润的预测值分别是多少?年宣传费x为何值时,年利润的预测值最大?
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)由散点图可以判断,y=c+d适宜作为年销售量y关于年宣传费x的经验回归方程类型.
(2)令w=,先建立y关于w的经验回归方程.
由于===68,
==563-68×6.8=100.6,
所以y关于w的经验回归方程为=100.6+68w,
因此y关于x的非线性经验回归方程为=100.6+68.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(3)由(2)知,当x=49时,
年销售量y的预测值=100.6+68=576.6,
年利润z的预测值=576.6×0.2-49=66.32.
根据(2)的结果知,年利润z的预测值
=0.2(100.6+68)-x=-x+13.6+20.12.
所以当==6.8,
即x=46.24时,取得最大值.
故年宣传费为46.24万元时,年利润的预测值最大.
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·上海卷)已知沿海地区气温和海水表层温度相关,且样本相关系数为正数,对此描述正确的是( )
A.沿海地区气温高,海水表层温度就高
B.沿海地区气温高,海水表层温度就低
C.随着沿海地区气温由低到高,海水表层温度呈上升趋势
D.随着沿海地区气温由低到高,海水表层温度呈下降趋势
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [对于AB,当沿海地区气温高时,海水表层温度变高变低不确定,故AB错误.
对于CD,因为样本相关系数为正,故随着气候温度由低到高,海水表层温度呈上升趋势,
故C正确,D错误.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2023·天津卷改编)调查某种群花萼长度和花瓣长度,所得数据如图所示.其中样本相关系数r=0.824 5,下列说法正确的是( )
A.花瓣长度和花萼长度没有相关性
B.花瓣长度和花萼长度负相关
C.花瓣长度和花萼长度正相关
D.若从样本中抽取一部分,则这部分的
样本相关系数一定是0.824 5
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为样本相关系数r=0.824 5接近1,所以花瓣长度和花萼长度的相关性较强,并且呈正相关,所以选项A,B错误,选项C正确;因为样本相关系数与样本的数据有关,所以当样本发生变化时,样本相关系数也会发生变化,所以选项D错误.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2023·上海卷)已知某校50名学生的身高与体重的散点图如图所示,则下列说法正确的是( )
A.身高越高,体重越重
B.身高越高,体重越轻
C.身高与体重成正相关
D.身高与体重成负相关
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [由题图可知,各数据分布呈线性,且从左向右看,呈现上升趋势,故身高与体重成正相关.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2024·新高考Ⅱ卷)某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:kg)并整理得下表:
亩产量 [900, 950) [950, 1 000) [1 000, 1 050) [1 050, 1 100) [1 100, 1 150) [1 150,
1 200)
频数 6 12 18 30 24 10
根据表中数据,下列结论中正确的是( )
A.100块稻田亩产量的中位数小于1 050 kg
B.100块稻田中亩产量低于1 100 kg的稻田所占比例超过80%
C.100块稻田亩产量的极差介于200 kg至300 kg之间
D.100块稻田亩产量的平均值介于900 kg至1 000 kg之间
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [对于A,根据频数分布表可知,6+12+18=36<50,
所以亩产量的中位数不小于1 050 kg,故A错误;
对于B,亩产量不低于1 100 kg的频数为24+10=34,
所以亩产量低于1 100 kg的稻田占比为=66%,故B错误;
对于C,稻田亩产量的极差最大为1 200-900=300,最小为1 150-950=200,故C正确;
对于D,平均值为×(6×925+12×975+18×1 025+30×1 075+24×
1 125+10×1 175)=1 067,故D错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2023·上海卷)国内生产总值(GDP)是衡量一个国家或地区经济状况和发展水平的重要指标.根据统计数据显示,某市在2020年间经济高质量增长,GDP稳定增长,第一季度和第四季度的GDP分别为232亿元和241亿元,且四个季度的GDP逐季度增长,中位数与平均数相等,则该市2020年的GDP总额为________亿元.
946
题号
1
3
5
2
4
6
8
7
9
10
11
12
946 [依题意,将2020年四个季度的GDP数据分别记为a1,a2,a3,
a4,则a1=232,a4=241,四个季度GDP数据的中位数为(a2+a3),平均数为(a1+a2+a3+a4),则(a2+a3)=(a1+a2+a3+a4),∴a2+
a3=a1+a4=473,故该市2020年的GDP总额为a1+a2+a3+a4=2(a1+a4)=946(亿元).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·春季上海卷)从某果园中采摘某种水果共136箱,每箱均装有相同个数的此种水果,此种水果分为一级果和二级果,其中一级果102箱,二级果34箱.
(1)随意挑选2箱此种水果,求恰好选到一级果和二级果各一箱的概率;
(2)若采用分层随机抽样的方法从中抽取8箱此种水果,求一级果和二级果各抽取几箱;
(3)若抽取若干箱此种水果,其中一级果共120个,单果质量平均数为303.45克,方差为603.46;二级果共48个,单果质量平均数为240.41克,方差为648.21.求168个此种水果单果质量的平均数和方差,并预估该果园中此种水果单果的质量.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)设“随意挑选2箱此种水果,恰好选到一级果和二级果各一
箱”为事件A,则P(A)==.
(2)抽取一级果的箱数为8×=6;
抽取二级果的箱数为8×=2.
(3)设一级果单果质量的平均数为,
则==≈285.44(克),
设一级果单果质量的方差为,二级果单果质量的方差为,
则=)2===648.21,
题号
1
3
5
2
4
6
8
7
9
10
11
12
设168个此种水果单果质量的方差为,则=×[603.46+(303.45-285.44)2]+[648.21+(240.41-285.44)2]≈1 427.27.
果园中此种水果单果质量的平均数为
==287.69(克).
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2023·全国甲卷改编)一项试验旨在研究臭氧效应,试验方案如下:选40只小白鼠,随机地将其中20只分配到试验组,另外20只分配到对照组,试验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g).试验结果如下:
对照组的小白鼠体重的增加量从小到大排序为
15.2 18.8 20.2 21.3 22.5 23.2 25.8
26.5 27.5 30.1 32.6 34.3 34.8 35.6
35.6 35.8 36.2 37.3 40.5 43.2
试验组的小白鼠体重的增加量从小到大排序为
7.8 9.2 11.4 12.4 13.2 15.5
16.5 18.0 18.8 19.2 19.8 20.2
21.6 22.8 23.6 23.9 25.1 28.2
32.3 36.5
(1)计算试验组的样本平均数;
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)(ⅰ)求40只小白鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于m的数据的个数,完成如下列联表:
单位:只
题号
1
3
5
2
4
6
8
7
9
10
11
12
试验 体重的增加量 合计
对照组
试验组
合计
(ⅱ)根据(ⅰ)中的列联表,依据小概率值α=0.05的独立性检验,能否认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异?
附:χ2=,
题号
1
3
5
2
4
6
8
7
9
10
11
12
α 0.100 0.050 0.010
xα 2.706 3.841 6.635
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)试验组的样本平均数为×(7.8+9.2+11.4+12.4+13.2+
15.5+16.5+18.0+18.8+19.2+19.8+20.2+21.6+22.8+23.6+23.9+25.1+28.2+32.3+36.5)=19.8.
(2)(ⅰ)将40个数据按照从小到大的顺序依次排列,得最中间的两个数据即第20个和第21个数据分别为23.2和23.6,则40只小白鼠体重的
增加量的中位数m==23.4.
题号
1
3
5
2
4
6
8
7
9
10
11
12
列联表如下:
单位:只
试验 体重的增加量 合计
对照组 6 14 20
试验组 14 6 20
合计 20 20 40
题号
1
3
5
2
4
6
8
7
9
10
11
12
(ⅱ)零假设为
H0:小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量无差异.
χ2===6.4>3.841,
依据小概率值α=0.05的独立性检验,推断H0不成立,即认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2023·新高考Ⅱ卷)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性,此检测标准的漏诊率是将患病者判定为阴性的概率,记为p(c);误诊率是将未患病者判定为阳性的概率,记为q(c).假设数据在组内均匀分布.以事件发生的频率作为相应事件发生的概率.
(1)当漏诊率p(c)=0.5%时,求临界值c和误诊率q(c);
(2)设函数f (c)=p(c)+q(c).当c∈[95,105]时,求f (c)的解析式,并求f (c)在区间[95,105]的最小值.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)由题图知(100-95)×0.002=1%>0.5%,所以95<c<100,
设X为患病者的该指标,
则p(c)=P(X≤c)=(c-95)×0.002=0.5%,
解得c=97.5.
设Y为未患病者的该指标,
则q(c)=P(Y>c)=(100-97.5)×0.01+5×0.002=0.035=3.5%.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)当95≤c≤100时,
p(c)=(c-95)×0.002=0.002c-0.19,
q(c)=(100-c)×0.01+5×0.002=-0.01c+1.01,
所以f (c)=p(c)+q(c)=-0.008c+0.82;
当100<c≤105时,
p(c)=5×0.002+(c-100)×0.012=0.012c-1.19,
q(c)=(105-c)×0.002=-0.002c+0.21,
所以f (c)=p(c)+q(c)=0.01c-0.98.
题号
1
3
5
2
4
6
8
7
9
10
11
12
综上所述,f (c)=
由一次函数的单调性知,函数f (c)在[95,100]上单调递减,在(100,105]上单调递增,作出f (c)在区间[95,105]上的大致图象(略),可得f (c)在区间[95,105]的最小值f (c)min=f (100)=
-0.008×100+0.82=0.02.
谢 谢 !
第十章 统计与成对数据的统计分析
阶段提能(十八) 概率与统计
1.(人教A版选择性必修第三册P104习题8.1T2)随机抽取10家航空公司,对其最近一年的航班正点率和顾客投诉次数进行调查,所得数据如下:
题号
1
3
5
2
4
6
8
7
9
10
11
12
航空公司编号 1 2 3 4 5 6 7 8 9 10
航班正点率/% 81.8 76.8 76.6 75.7 73.8 72.2 71.2 70.8 91.4 68.5
顾客投诉/次 21 58 85 68 74 93 72 122 18 125
顾客投诉次数和航班正点率之间是否呈现出线性相关关系?它们之间的相关程度如何?变化趋势有何特征?
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] 先画顾客投诉次数和航班正点率的散点图,如图所示.
从散点分布可以看出顾客投诉次数和航班正点率负相关.
下面通过计算,严格说明这一结论.
设航班正点率为x,顾客投诉次数为y.
由数据可得=73.6,=53 978.3,
=57 975.1,=65 796,
∴r==
≈-0.87.
由此可以推断,顾客投诉次数与航班正点率之间呈现出线性相关关系,相关程度较强,且为负相关,顾客投诉次数与航班正点率的变化趋势相反.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
2.(北师大版选择性必修第一册P241习题7-1T1)一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
零件数x/个 10 20 30 40 50
加工时间y/min 62 68 75 81 89
零件数x/个 60 70 80 90 100
加工时间y/min 95 102 108 115 122
(1)画出散点图;
(2)求y关于x的经验回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
[解] (1)散点图如下.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)由已知得=91.7,
)=5 515,
)2=8 250,所以=≈0.668,
≈91.7-0.668×55=54.96.
所以经验回归方程为=0.668x+54.96.
(3)关于加工零件的个数与加工时间,我们得到的结论是:加工的零件越多,所花的时间大致越长.
题号
1
3
5
2
4
6
8
7
9
10
11
12
3.(人教B版选择性必修第二册P122习题4-3BT4)某工厂有25周岁及以上的工人300名,25周岁以下的工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层随机抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁及以上”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下”的工人的概率;
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件列出2×2列联表,依据小概率值α=0.1的独立性检验,能否认为“生产能手”与工人所在的年龄组有关.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)由已知得样本中有25周岁及以上组工人60名,25周岁以下组工人40名,所以样本中日平均生产件数不足60件的工人中25周岁及以上组有60×0.05=3(人),分别记为A1,A2,A3,25周岁以下组有40×0.05=2(人),分别记为B1,B2,从中随机抽取2人,所有可能的结果共10种,分别是(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),其中至少抽到1名25周岁以下组的工
人的结果有7种,故所求概率P=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)由频率分布直方图可知在抽取的100名工人中,
“25周岁及以上组”中的“生产能手”有60×0.25=15(人),
“25周岁以下组”中的“生产能手”有40×0.375=15(人),
据此可得2×2列联表:
单位:人
分组 生产件数 合计
≥80 <80
25周岁及以上组 15 45 60
25周岁以下组 15 25 40
合计 30 70 100
题号
1
3
5
2
4
6
8
7
9
10
11
12
零假设为
H0:“生产能手”与工人所在的年龄组无关.
χ2==≈1.786<2.706.
所以依据小概率值α=0.1的独立性检验,没有充分证据推断H0不成立,即认为“生产能手”与工人所在的年龄组无关.
题号
1
3
5
2
4
6
8
7
9
10
11
12
4.(人教B版选择性必修第二册P128复习题C组T1)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:t)和年利润z(单位:万元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据进行了初步处理,得到下面的散点图及一些统计量的值.
表中wi==
·
46.6 563 6.8 289.8 1.6 1 469 108.8
题号
1
3
5
2
4
6
8
7
9
10
11
12
(1)根据散点图判断,y=a+bx与y=c+d哪一个适宜作为年销售量y关于年宣传费x的经验回归方程类型?
(2)根据(1)的判断结果及表中数据,建立y关于x的经验回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:年宣传费x=49时,年销售量及年利润的预测值分别是多少?年宣传费x为何值时,年利润的预测值最大?
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)由散点图可以判断,y=c+d适宜作为年销售量y关于年宣传费x的经验回归方程类型.
(2)令w=,先建立y关于w的经验回归方程.
由于===68,
==563-68×6.8=100.6,
所以y关于w的经验回归方程为=100.6+68w,
因此y关于x的非线性经验回归方程为=100.6+68.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(3)由(2)知,当x=49时,
年销售量y的预测值=100.6+68=576.6,
年利润z的预测值=576.6×0.2-49=66.32.
根据(2)的结果知,年利润z的预测值
=0.2(100.6+68)-x=-x+13.6+20.12.
所以当==6.8,
即x=46.24时,取得最大值.
故年宣传费为46.24万元时,年利润的预测值最大.
题号
1
3
5
2
4
6
8
7
9
10
11
12
5.(2024·上海卷)已知沿海地区气温和海水表层温度相关,且样本相关系数为正数,对此描述正确的是( )
A.沿海地区气温高,海水表层温度就高
B.沿海地区气温高,海水表层温度就低
C.随着沿海地区气温由低到高,海水表层温度呈上升趋势
D.随着沿海地区气温由低到高,海水表层温度呈下降趋势
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [对于AB,当沿海地区气温高时,海水表层温度变高变低不确定,故AB错误.
对于CD,因为样本相关系数为正,故随着气候温度由低到高,海水表层温度呈上升趋势,
故C正确,D错误.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
6.(2023·天津卷改编)调查某种群花萼长度和花瓣长度,所得数据如图所示.其中样本相关系数r=0.824 5,下列说法正确的是( )
A.花瓣长度和花萼长度没有相关性
B.花瓣长度和花萼长度负相关
C.花瓣长度和花萼长度正相关
D.若从样本中抽取一部分,则这部分的
样本相关系数一定是0.824 5
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [因为样本相关系数r=0.824 5接近1,所以花瓣长度和花萼长度的相关性较强,并且呈正相关,所以选项A,B错误,选项C正确;因为样本相关系数与样本的数据有关,所以当样本发生变化时,样本相关系数也会发生变化,所以选项D错误.
故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
7.(2023·上海卷)已知某校50名学生的身高与体重的散点图如图所示,则下列说法正确的是( )
A.身高越高,体重越重
B.身高越高,体重越轻
C.身高与体重成正相关
D.身高与体重成负相关
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [由题图可知,各数据分布呈线性,且从左向右看,呈现上升趋势,故身高与体重成正相关.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
8.(2024·新高考Ⅱ卷)某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:kg)并整理得下表:
亩产量 [900, 950) [950, 1 000) [1 000, 1 050) [1 050, 1 100) [1 100, 1 150) [1 150,
1 200)
频数 6 12 18 30 24 10
根据表中数据,下列结论中正确的是( )
A.100块稻田亩产量的中位数小于1 050 kg
B.100块稻田中亩产量低于1 100 kg的稻田所占比例超过80%
C.100块稻田亩产量的极差介于200 kg至300 kg之间
D.100块稻田亩产量的平均值介于900 kg至1 000 kg之间
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
C [对于A,根据频数分布表可知,6+12+18=36<50,
所以亩产量的中位数不小于1 050 kg,故A错误;
对于B,亩产量不低于1 100 kg的频数为24+10=34,
所以亩产量低于1 100 kg的稻田占比为=66%,故B错误;
对于C,稻田亩产量的极差最大为1 200-900=300,最小为1 150-950=200,故C正确;
对于D,平均值为×(6×925+12×975+18×1 025+30×1 075+24×
1 125+10×1 175)=1 067,故D错误.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
9.(2023·上海卷)国内生产总值(GDP)是衡量一个国家或地区经济状况和发展水平的重要指标.根据统计数据显示,某市在2020年间经济高质量增长,GDP稳定增长,第一季度和第四季度的GDP分别为232亿元和241亿元,且四个季度的GDP逐季度增长,中位数与平均数相等,则该市2020年的GDP总额为________亿元.
946
题号
1
3
5
2
4
6
8
7
9
10
11
12
946 [依题意,将2020年四个季度的GDP数据分别记为a1,a2,a3,
a4,则a1=232,a4=241,四个季度GDP数据的中位数为(a2+a3),平均数为(a1+a2+a3+a4),则(a2+a3)=(a1+a2+a3+a4),∴a2+
a3=a1+a4=473,故该市2020年的GDP总额为a1+a2+a3+a4=2(a1+a4)=946(亿元).]
题号
1
3
5
2
4
6
8
7
9
10
11
12
10.(2024·春季上海卷)从某果园中采摘某种水果共136箱,每箱均装有相同个数的此种水果,此种水果分为一级果和二级果,其中一级果102箱,二级果34箱.
(1)随意挑选2箱此种水果,求恰好选到一级果和二级果各一箱的概率;
(2)若采用分层随机抽样的方法从中抽取8箱此种水果,求一级果和二级果各抽取几箱;
(3)若抽取若干箱此种水果,其中一级果共120个,单果质量平均数为303.45克,方差为603.46;二级果共48个,单果质量平均数为240.41克,方差为648.21.求168个此种水果单果质量的平均数和方差,并预估该果园中此种水果单果的质量.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)设“随意挑选2箱此种水果,恰好选到一级果和二级果各一
箱”为事件A,则P(A)==.
(2)抽取一级果的箱数为8×=6;
抽取二级果的箱数为8×=2.
(3)设一级果单果质量的平均数为,
则==≈285.44(克),
设一级果单果质量的方差为,二级果单果质量的方差为,
则=)2===648.21,
题号
1
3
5
2
4
6
8
7
9
10
11
12
设168个此种水果单果质量的方差为,则=×[603.46+(303.45-285.44)2]+[648.21+(240.41-285.44)2]≈1 427.27.
果园中此种水果单果质量的平均数为
==287.69(克).
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
11.(2023·全国甲卷改编)一项试验旨在研究臭氧效应,试验方案如下:选40只小白鼠,随机地将其中20只分配到试验组,另外20只分配到对照组,试验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位:g).试验结果如下:
对照组的小白鼠体重的增加量从小到大排序为
15.2 18.8 20.2 21.3 22.5 23.2 25.8
26.5 27.5 30.1 32.6 34.3 34.8 35.6
35.6 35.8 36.2 37.3 40.5 43.2
试验组的小白鼠体重的增加量从小到大排序为
7.8 9.2 11.4 12.4 13.2 15.5
16.5 18.0 18.8 19.2 19.8 20.2
21.6 22.8 23.6 23.9 25.1 28.2
32.3 36.5
(1)计算试验组的样本平均数;
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)(ⅰ)求40只小白鼠体重的增加量的中位数m,再分别统计两样本中小于m与不小于m的数据的个数,完成如下列联表:
单位:只
题号
1
3
5
2
4
6
8
7
9
10
11
12
试验 体重的增加量 合计
试验组
合计
(ⅱ)根据(ⅰ)中的列联表,依据小概率值α=0.05的独立性检验,能否认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异?
附:χ2=,
题号
1
3
5
2
4
6
8
7
9
10
11
12
α 0.100 0.050 0.010
xα 2.706 3.841 6.635
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)试验组的样本平均数为×(7.8+9.2+11.4+12.4+13.2+
15.5+16.5+18.0+18.8+19.2+19.8+20.2+21.6+22.8+23.6+23.9+25.1+28.2+32.3+36.5)=19.8.
(2)(ⅰ)将40个数据按照从小到大的顺序依次排列,得最中间的两个数据即第20个和第21个数据分别为23.2和23.6,则40只小白鼠体重的
增加量的中位数m==23.4.
题号
1
3
5
2
4
6
8
7
9
10
11
12
列联表如下:
单位:只
试验 体重的增加量 合计
试验组 14 6 20
合计 20 20 40
题号
1
3
5
2
4
6
8
7
9
10
11
12
(ⅱ)零假设为
H0:小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量无差异.
χ2===6.4>3.841,
依据小概率值α=0.05的独立性检验,推断H0不成立,即认为小白鼠在高浓度臭氧环境中与在正常环境中体重的增加量有差异.
题号
1
3
5
2
4
6
8
7
9
10
11
12
12.(2023·新高考Ⅱ卷)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性,此检测标准的漏诊率是将患病者判定为阴性的概率,记为p(c);误诊率是将未患病者判定为阳性的概率,记为q(c).假设数据在组内均匀分布.以事件发生的频率作为相应事件发生的概率.
(1)当漏诊率p(c)=0.5%时,求临界值c和误诊率q(c);
(2)设函数f (c)=p(c)+q(c).当c∈[95,105]时,求f (c)的解析式,并求f (c)在区间[95,105]的最小值.
题号
1
3
5
2
4
6
8
7
9
10
11
12
题号
1
3
5
2
4
6
8
7
9
10
11
12
[解] (1)由题图知(100-95)×0.002=1%>0.5%,所以95<c<100,
设X为患病者的该指标,
则p(c)=P(X≤c)=(c-95)×0.002=0.5%,
解得c=97.5.
设Y为未患病者的该指标,
则q(c)=P(Y>c)=(100-97.5)×0.01+5×0.002=0.035=3.5%.
题号
1
3
5
2
4
6
8
7
9
10
11
12
(2)当95≤c≤100时,
p(c)=(c-95)×0.002=0.002c-0.19,
q(c)=(100-c)×0.01+5×0.002=-0.01c+1.01,
所以f (c)=p(c)+q(c)=-0.008c+0.82;
当100<c≤105时,
p(c)=5×0.002+(c-100)×0.012=0.012c-1.19,
q(c)=(105-c)×0.002=-0.002c+0.21,
所以f (c)=p(c)+q(c)=0.01c-0.98.
题号
1
3
5
2
4
6
8
7
9
10
11
12
综上所述,f (c)=
由一次函数的单调性知,函数f (c)在[95,100]上单调递减,在(100,105]上单调递增,作出f (c)在区间[95,105]上的大致图象(略),可得f (c)在区间[95,105]的最小值f (c)min=f (100)=
-0.008×100+0.82=0.02.
谢 谢 !
同课章节目录
