《高考快车道》2026版高三一轮总复习数学(基础版)117 第十章 滚动测试卷(七) 第一~十章 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)117 第十章 滚动测试卷(七) 第一~十章 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:09 | ||
图片预览










文档简介
(共56张PPT)
第十章 统计与成对数据的统计分析
滚动测试卷(七) 第一~十章
单元检测(一)
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
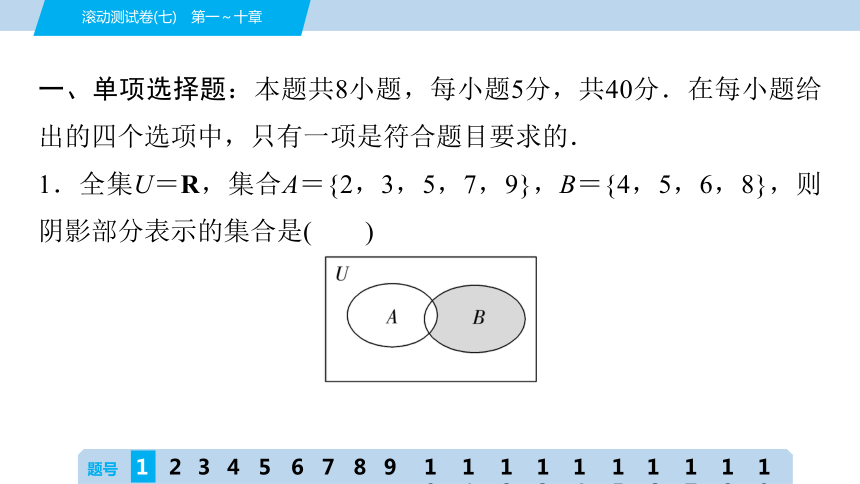
1.全集U=R,集合A={2,3,5,7,9},B={4,5,6,8},则阴影部分表示的集合是( )
A.{2,3,5,7,9} B.{2,3,4,5,6,7,8,9}
C.{4,6,8} D.{5}
√
C [Venn图的阴影部分表示的集合为( UA)∩B,而全集U=R,集合A={2,3,5,7,9},B={4,5,6,8},
所以( UA)∩B={4,6,8}.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
2.样本数据16,24,14,10,20,30,12,14,40的中位数为( )
A.14 B.16
C.18 D.20
B [将这些数据按从小到大排列可得:10,12,14,14,16,20,24,30,40,则其中位数为16.故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
3.已知i为复数单位,=2+i,则z=1+ai的模为( )
A. B.1
C.2 D.4
A [由=2+i,可得3+ai=(2+i)(1-i)=3-i,所以a=-1,
所以z=1-i,则|z|==.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
4.(2025·青岛模拟)通过随机询问某中学110名中学生是否爱好跳绳,得到如下列联表:
单位:人
跳绳 性别 合计
男 女
爱好 40 20 60
不爱好 20 30 50
合计 60 50 110
已知χ2=,P(χ2≥10.828)=0.001,依据小概率值α
=0.001的χ2独立性检验,以下结论正确的为( )
A.爱好跳绳与性别有关
B.爱好跳绳与性别有关,这个结论犯错误的概率不超过0.001
C.爱好跳绳与性别无关
D.爱好跳绳与性别无关,这个结论犯错误的概率不超过0.001
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
C [χ2==≈7.822<10.828,
故爱好跳绳与性别无关,但不能推出这个结论犯错误的概率不超过0.001,故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
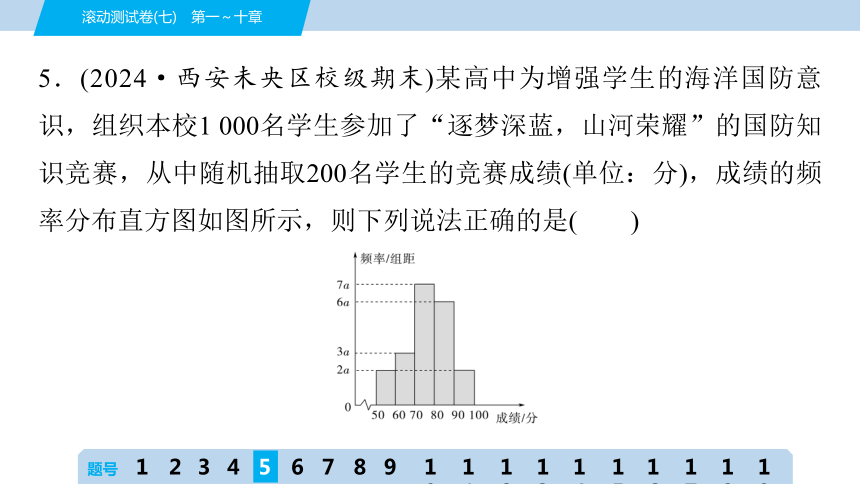
5.(2024·西安未央区校级期末)某高中为增强学生的海洋国防意识,组织本校1 000名学生参加了“逐梦深蓝,山河荣耀”的国防知识竞赛,从中随机抽取200名学生的竞赛成绩(单位:分),成绩的频率分布直方图如图所示,则下列说法正确的是( )
①频率分布直方图中a的值为0.005;
②估计这200名学生竞赛成绩的第60百分位数为80;
③估计这200名学生竞赛成绩的众数为78;
④估计总体中成绩落在[60,70)内的学生人数为150.
A.①②③ B.①②④
C.①③④ D.②④
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
B [对于①,∵(2a+3a+7a+6a+2a)×10=1,∴a=0.005,∴①正确;
对于②,前3组的频率和为0.1+0.15+0.35=0.6,
∴估计这200名学生竞赛成绩的第60百分位数为80,∴②正确;
对于③,由题干图可估计这200名学生竞赛成绩的众数为=75,∴③错误;
对于④,∵样本中成绩落在[60,70)内的频率为30a=0.15,
∴估计总体中成绩落在[60,70)内的学生人数为1 000×0.15=150,∴④正确.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
6.已知数列{an}和{bn}均为等差数列,数列{an}的前n项和为Sn,若为定值,S5=45,b3=6,b7=14,则a5=( )
A.15 B.56
C.72 D.104
A [在等差数列{an}中,由S5==5a3=45,得a3=9,
因为为定值,所以===,
即a7=21,
所以a5==15.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
7.(2024·常州武进区期末)已知某班级参与定点投篮比赛的学生共有20名,进球数的平均值和方差分别是4和3.6,其中男生进球数的平均值和方差分别是5和1.8,女生进球数的平均值为3,则女生进球数的方差为( )
A.3.2 B.3.4
C.3.6 D.3.8
B [设男生的人数为x,女生的人数为y,
由题意可知,解得
设女生进球数的方差为s2,
20名学生进球数的平均值和方差分别是4和3.6,其中男生进球数的
平均值和方差分别是5和1.8,女生进球数的平均值为3,则×[1.8+(5-4)2]+×[s2+(3-4)2]=3.6,解得s2=3.4.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
8.已知函数y=ex的图象在点P(0,1)处的切线与圆心为Q(1,0)的圆相切,则圆Q的面积是( )
A.π B.2π
C.3π D.4π
B [依题意,y′=ex,则函数y=ex的图象在点P(0,1)处的切线斜率为:k=y′|x=0=e0=1,
所以函数y=ex的图象在点P(0,1)处的切线方程为y-1=1×(x-0),即x-y+1=0,
因为该切线x-y+1=0与圆心为Q(1,0)的圆相切,所以圆的半径
r==,
所以圆Q的面积为πr2=2π.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.经过简单随机抽样获得的样本数据为x1,x2,…,xn,则下列说法正确的是( )
A.若数据x1,x2,…,xn的方差s2=0,则x1=x2=…=xn
B.若数据x1,x2,…,xn的均值为3,则数据y1,y2,…,yn(其中yi=2xi+1(i=1,2,…,n))的均值为6
C.若数据x1,x2,…,xn的中位数为90,则可以估计总体中至少有50%的数据不大于90
D.若数据x1,x2,…,xn的众数为78,则可以说总体中的众数为78
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
AC [对于A,数据x1,x2,…,xn的方差s2=0,则x1=x2=…=xn,所以选项A正确;对于B,数据x1,x2,…,xn的均值为3,则数据y1,y2,…,yn(其中yi=2xi+1(i=1,2,…,n))的均值为2×3+1=7,所以选项B错误;对于C,数据x1,x2,…,xn的中位数为90,则根据中位数的定义可以估计总体中至少有50%的数据不大于90,所以选项C正确;对于D,样本数据具有随机性,所以样本的众数不一定是总体的众数,所以选项D错误.故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
10.(2024·内江月考)为调研加工零件效率,调研员通过试验获得加工零件个数x与所用时间y(单位:min)的5组数据为:(1,5),(2,9),(3,12),(4,15),(5,19),根据以上数据可得经验回归方程为=3.4x+,则下列选项正确的有( )
A.=1.8
B.经验回归直线=3.4x+必过点(2,9)
C.加工6个零件的时间大约为22.2 min
D.若去掉(3,12),剩下4组数据的经验回归方程不会有变化
√
√
ACD [=(5+9+12+15+19)=
12,所以经验回归直线=3.4x+恒过点(3,12),所以12=3.4×3+,解得=1.8,故A正确;
当x=2时,=3.4×2+1.8=8.6≠9,故B错误;
由=3.4x+1.8,令x=6,则=3.4×6+1.8=22.2,
故加工6个零件的时间大约为22.2 min,故C正确;
因为经验回归直线=3.4x+1.8恒过点(3,12),所以剩下4组数据的经验回归方程不会有变化,故D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
11.若实数aA.<<
B.若a>1,则logaab>2
C.若a>0,则>
D.若m>,a,b∈(1,3),则(a3-b3)-m(a2-b2)+a-b>0
√
√
BCD [对于A,当a=0时,=,所以选项A错误;对于B,
因为a>1,b>a,所以ab>a2>1,又y=logax为增函数,
所以logaab>logaa2=2,所以选项B正确;
对于C,==
=,因为a>0,b>a,所以b>a>0,b-a>0,
所以(1+a)(1+b)>0,b2+a2+ab+a+b>0,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
所以>0,即>0,即>,所以选项C正确;对于D,(a3-b3)-m(a2-b2)+a-b=a3-ma2+a-,令f (x)=x3-mx2+x,则f ′(x)=x2-2mx+1,因为m>,所以f ′(1)=2-2m<2-<0,f ′(3)=10-6m<10-6×=0,所以f ′(x)<0在(1,3)上恒成立,所以函数f (x)在(1,3)上单调递减.又1f (b),即-mb2+b,所以(a3-b3)-m(a2-b2)+a-b=a3-ma2+a->0,所以选项D正确.故选BCD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
三、填空题:本题共3小题,每小题5分,共15分.
12.(2024·台州期末)某学校有高二学生600人,其中男生360人,女生240人.有人为了获得该校全体高二学生的身高信息,采用分层随机抽样的方法抽取了容量为100的总样本(观测数据单位:cm),若已知男生样本的平均数为172,女生样本的平均数为162,则总样本的平均数是________.
168
168 [男生样本的平均数为172,女生样本的平均数为162,
则总样本的平均数是:×172+×162=168.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
13.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数,如下表:
天数x 1 2 3 4 5 6 7
一次最多答 对题数y 12 15 16 18 21 24 27
由表中数据可知该老师每天一次最多答对题数y与天数x之间是________相关(填“正”或“负”),其样本相关系数r≈________(结果保留两位小数).
正
0.99
参考数据:=4,=19,=140,=2 695,
xiyi=600,≈2.45,
样本相关系数r=.
正 0.99 [由表中数据知,y随x的增大而增大,
所以该老师每天一次最多答对题数y与天数x之间是正相关.
r==≈0.99.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
14.已知双曲线方程为=1(a>0,b>0),左焦点F关于一条渐
近线的对称点在另一条渐近线上,则该双曲线的离心率为_______.
2 [如图,设F关于渐近线y=x对称的点A在渐近线y=-x上,
2
FA的中点B在渐近线y=x上,
则∠FOB=∠BOA,
又∠FOB=∠AOx,
所以∠FOB=∠BOA=∠AOx=60°,
所以tan 60°==,
所以e=====2.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)每年的11月9日为“119消防宣传日”.消防宣传日的设立,旨在提醒全民关注消防安全,学习消防知识,提高自救互救能力,减少火灾事故的发生.某高中学校为增强学生的消防安全意识,组织本校高一、高二共800名学生参加“消防安全,在我心中”的知识竞赛,现从每个年级分别随机抽取10名学生的竞赛成绩如下:
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
高一:90 85 82 85 97 83 88 95 90 85
高二:83 90 97 88 95 85 95 85 80 82
(1)请根据以上20个数据,估计此次参赛学生成绩的第60百分位数、众数和平均数;
(2)若规定95分及以上为一等奖,从一等奖的学生中任选2人作为宣讲代表,则这2人中至少有1人来自高一年级的概率是多少?
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
[解] (1)把20个数据由小到大排列为80,82,82,83,83,85,85,85,85,85,88,88,90,90,90,95,95,95,97,97,由20×60%=12,
估计此次参赛学生成绩的第60百分位数为=89,
估计此次参赛学生成绩的众数为85,
平均数为=(80+82×2+83×2+85×5+88×2+90×3+95×3+
97×2)=88.
(2)成绩在95分及以上的有5人,来自高一年级的有2人,记为1,2,
来自高二年级的有3人,记为a,b,c,
从5人中任选2人的样本空间为:
Ω={12,1a,1b,1c,2a,2b,2c,ab,ac,bc},共10个样本点,
设事件A表示“这2人中至少有1人来自高一年级”,
则A={12,1a,1b,1c,2a,2b,2c},共7个样本点,
∴这2人中至少有1人来自高一年级的概率是P(A)=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
16.(15分)(2024·北京西城区模拟)每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.A校为了了解学生的课外阅读情况,随机调查了n名学生,发现这些学生的课外日均阅读时间(单位:分钟)均在[0,120].根据这n名学生的课外日均阅读时间,将样本数据分组为:[0,20),[20,40),[40,60),[60,80),[80,100),[100,120],并绘制出如下频率分布表.
分组 频数 频率
[0,20) 4 f1
[20,40) 10 0.1
[40,60) 46 f2
[60,80) a f3
[80,100) 20 f4
[100,120] 4 f5
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(1)求n,f3的值;
(2)若采用分层随机抽样的方法从课外日均阅读时间为[60,80),[80,100),[100,120]的学生中抽取10人,再从抽取的10名学生中随机抽取1名学生进行阅读经验分享,求抽到做阅读经验分享的学生的课外日均阅读时间不少于80分钟的概率;
(3)现从这n名学生中评出课外日均阅读时间较长的10人为“阅读达人”,请算出要成为“阅读达人”至少需要的课外日均阅读时间.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
[解] (1)因为数据在[20,40)内的频数为10,频率为0.1,
所以=0.1 n=100,
则4+10+46+a+20+4=100 a=16,所以f3==0.16.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)因为课外日均阅读时间在[60,80),[80,100),[100,120]的学生比例为16∶20∶4=4∶5∶1,
所以采用分层随机抽样的方法从课外日均阅读时间为[60,80),[80,100),[100,120]的学生中抽取10人,
日均阅读时间在[60,80),[80,100),[100,120]的人数分别为4,5,1,则课外日均阅读时间不少于80分钟的人数为6人,
抽到做阅读经验分享的学生的课外日均阅读时间不少于80分钟的概
率为=0.6.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(3)这n名学生中评出课外日均阅读时间较长的10人为“阅读达人”,日均阅读时间在[100,120]的学生人数为4人,
再从日均阅读时间在[80,100)的学生中选出6个阅读时间较长的人即可,
设6个人中阅读时间最短的是x分钟,则= x=94,
所以成为“阅读达人”需要的课外日均阅读时间至少94分钟.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
17.(15分)某电商平台统计了近七年小家电的年度广告费支出xi(单位:万元)与年度销售量yi(单位:万台)的数据,如表所示:
年份 2018 2019 2020 2021 2022 2023 2024
广告费支 出x/万元 1 2 4 6 11 13 19
销售量 y/万台 1.9 3.2 4.0 4.4 5.2 5.3 5.4
其中xiyi=279.4,=708.
(1)若用线性经验回归模型拟合y与x的关系,求出y关于x的经验回归方程;
(2)若用y=c+d模型拟合得到的非线性经验回归方程为=1.63+0.99,经计算线性经验回归模型及该模型的R2分别为0.75和0.88,请根据R2的数值选择更好的经验回归模型拟合y与x的关系,进而计算出年度广告费x为何值时,利润=200y-x的预报值最大?
参考公式:==,=-.
[解] (1)由题意可得:
==8,==4.2,
所以===0.17,
==4.2-0.17×8=2.84,
所以y关于x的经验回归方程为=0.17x+2.84.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)因为0.75<0.88,R2越大,拟合效果越好,所以选用非线性经验回归方程=1.63+0.99更好,
=200(1.63+0.99)-x=-x+198+326,
=-(-99)2+10 127,
所以当=99,即x=9 801时,利润的预报值最大.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
18.(17分)如图,在多面体ABCDEF中,四边形ABCD与ABEF均为直角梯形,AD∥BC,AF∥BE,DA⊥平面ABEF,AB⊥AF,AD=AB=2BC=2BE=2.
(1)已知点G为AF上一点,且AG=2,
求证:BG与平面DCE不平行;
(2)已知直线BF与平面DCE所成角的正弦值
为,求AF的长及四棱锥D-ABEF的体积.
[解] (1)证明:因为DA⊥平面ABEF,AB,AF 平面ABEF,
所以DA⊥AB,DA⊥AF,又AB⊥AF,所以AB,AF,DA两两垂直.
以A为坐标原点,AF,AB,AD所在直线分别为x,y,z轴,建立空间直角坐标系,
则B(0,2,0),E(1,2,0),
C(0,2,1),D(0,0,2),G(2,0,0),
所以=(-1,0,1),=(-1,-2,2),
=(2,-2,0).
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
设平面DCE的法向量为n=(x,y,z),
则
令x=2,则z=2,y=1,所以n=(2,1,2)为平面DCE的一个法向量,
因为n·=2×2+1×(-2)=2≠0,
所以与n不垂直,
所以BG与平面DCE不平行.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)设AF=a(a>0且a≠1),则F (a,0,0),所以=(a,-2,0),
∵直线BF与平面DCE所成角的正弦值为,
∴==
==,
化简得11a2-40a-16=0,解得a=4或a=-(舍去),故AF=4.
此时S梯形ABEF=×(1+4)×2=5,故VD-ABEF=S梯形ABEF·DA=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
19.(17分)(2024·嘉兴二模)春季流感对广大民众的健康生活带来一定的影响,为了有效预防流感,很多民众注射了流感疫苗.某市防疫部门从辖区居民中随机抽取了1 000人进行调查,发现其中注射疫苗的800人中有220人感染流感,另外没注射疫苗的200人中有80人感染流感.医学研究表明,流感的检测结果有错检的可能,已知患有流感的人其检
测结果有95%呈阳性(感染),而没有患流感的人其检测结果有99%呈阴性(未感染).
(1)估计该市流感感染率是多少?
(2)依据小概率值α=0.001的独立性检验,能否认为注射流感疫苗与预防流感有关?
(3)已知某人的流感检测结果呈阳性,求此人真的患有流感的概率.(精确到0.001)
附:χ2=,
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
[解] (1)估计流感的感染率P==0.3.
(2)根据题意,得到2×2列联表如下:
单位:人
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
疫苗 流感 合计
患流感 不患流感
打疫苗 220 580 800
不打疫苗 80 120 200
合计 300 700 1 000
零假设为
H0:注射流感疫苗与预防流感无关.
χ2==≈11.905,
因为11.905>10.828,
所以依据小概率值α=0.001的独立性检验,推断H0不成立,即认为注射流感疫苗与预防流感有关.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(3)设事件A为“一次检测结果呈阳性”,事件B为“被检测者确实患有流感”,
由题意得P(B)=0.3,P()=0.01,
由全概率公式得P(A)=P(B)·P(A|B)+P()=0.3×0.95+0.7×0.01=0.292,
所以P(B|A)===≈97.6%,
即此人真的患有流感的概率是97.6%.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
谢 谢 !
第十章 统计与成对数据的统计分析
滚动测试卷(七) 第一~十章
单元检测(一)
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.全集U=R,集合A={2,3,5,7,9},B={4,5,6,8},则阴影部分表示的集合是( )
A.{2,3,5,7,9} B.{2,3,4,5,6,7,8,9}
C.{4,6,8} D.{5}
√
C [Venn图的阴影部分表示的集合为( UA)∩B,而全集U=R,集合A={2,3,5,7,9},B={4,5,6,8},
所以( UA)∩B={4,6,8}.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
2.样本数据16,24,14,10,20,30,12,14,40的中位数为( )
A.14 B.16
C.18 D.20
B [将这些数据按从小到大排列可得:10,12,14,14,16,20,24,30,40,则其中位数为16.故选B.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
3.已知i为复数单位,=2+i,则z=1+ai的模为( )
A. B.1
C.2 D.4
A [由=2+i,可得3+ai=(2+i)(1-i)=3-i,所以a=-1,
所以z=1-i,则|z|==.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
4.(2025·青岛模拟)通过随机询问某中学110名中学生是否爱好跳绳,得到如下列联表:
单位:人
跳绳 性别 合计
男 女
爱好 40 20 60
不爱好 20 30 50
合计 60 50 110
已知χ2=,P(χ2≥10.828)=0.001,依据小概率值α
=0.001的χ2独立性检验,以下结论正确的为( )
A.爱好跳绳与性别有关
B.爱好跳绳与性别有关,这个结论犯错误的概率不超过0.001
C.爱好跳绳与性别无关
D.爱好跳绳与性别无关,这个结论犯错误的概率不超过0.001
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
C [χ2==≈7.822<10.828,
故爱好跳绳与性别无关,但不能推出这个结论犯错误的概率不超过0.001,故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
5.(2024·西安未央区校级期末)某高中为增强学生的海洋国防意识,组织本校1 000名学生参加了“逐梦深蓝,山河荣耀”的国防知识竞赛,从中随机抽取200名学生的竞赛成绩(单位:分),成绩的频率分布直方图如图所示,则下列说法正确的是( )
①频率分布直方图中a的值为0.005;
②估计这200名学生竞赛成绩的第60百分位数为80;
③估计这200名学生竞赛成绩的众数为78;
④估计总体中成绩落在[60,70)内的学生人数为150.
A.①②③ B.①②④
C.①③④ D.②④
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
B [对于①,∵(2a+3a+7a+6a+2a)×10=1,∴a=0.005,∴①正确;
对于②,前3组的频率和为0.1+0.15+0.35=0.6,
∴估计这200名学生竞赛成绩的第60百分位数为80,∴②正确;
对于③,由题干图可估计这200名学生竞赛成绩的众数为=75,∴③错误;
对于④,∵样本中成绩落在[60,70)内的频率为30a=0.15,
∴估计总体中成绩落在[60,70)内的学生人数为1 000×0.15=150,∴④正确.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
6.已知数列{an}和{bn}均为等差数列,数列{an}的前n项和为Sn,若为定值,S5=45,b3=6,b7=14,则a5=( )
A.15 B.56
C.72 D.104
A [在等差数列{an}中,由S5==5a3=45,得a3=9,
因为为定值,所以===,
即a7=21,
所以a5==15.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
7.(2024·常州武进区期末)已知某班级参与定点投篮比赛的学生共有20名,进球数的平均值和方差分别是4和3.6,其中男生进球数的平均值和方差分别是5和1.8,女生进球数的平均值为3,则女生进球数的方差为( )
A.3.2 B.3.4
C.3.6 D.3.8
B [设男生的人数为x,女生的人数为y,
由题意可知,解得
设女生进球数的方差为s2,
20名学生进球数的平均值和方差分别是4和3.6,其中男生进球数的
平均值和方差分别是5和1.8,女生进球数的平均值为3,则×[1.8+(5-4)2]+×[s2+(3-4)2]=3.6,解得s2=3.4.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
8.已知函数y=ex的图象在点P(0,1)处的切线与圆心为Q(1,0)的圆相切,则圆Q的面积是( )
A.π B.2π
C.3π D.4π
B [依题意,y′=ex,则函数y=ex的图象在点P(0,1)处的切线斜率为:k=y′|x=0=e0=1,
所以函数y=ex的图象在点P(0,1)处的切线方程为y-1=1×(x-0),即x-y+1=0,
因为该切线x-y+1=0与圆心为Q(1,0)的圆相切,所以圆的半径
r==,
所以圆Q的面积为πr2=2π.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.经过简单随机抽样获得的样本数据为x1,x2,…,xn,则下列说法正确的是( )
A.若数据x1,x2,…,xn的方差s2=0,则x1=x2=…=xn
B.若数据x1,x2,…,xn的均值为3,则数据y1,y2,…,yn(其中yi=2xi+1(i=1,2,…,n))的均值为6
C.若数据x1,x2,…,xn的中位数为90,则可以估计总体中至少有50%的数据不大于90
D.若数据x1,x2,…,xn的众数为78,则可以说总体中的众数为78
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
AC [对于A,数据x1,x2,…,xn的方差s2=0,则x1=x2=…=xn,所以选项A正确;对于B,数据x1,x2,…,xn的均值为3,则数据y1,y2,…,yn(其中yi=2xi+1(i=1,2,…,n))的均值为2×3+1=7,所以选项B错误;对于C,数据x1,x2,…,xn的中位数为90,则根据中位数的定义可以估计总体中至少有50%的数据不大于90,所以选项C正确;对于D,样本数据具有随机性,所以样本的众数不一定是总体的众数,所以选项D错误.故选AC.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
10.(2024·内江月考)为调研加工零件效率,调研员通过试验获得加工零件个数x与所用时间y(单位:min)的5组数据为:(1,5),(2,9),(3,12),(4,15),(5,19),根据以上数据可得经验回归方程为=3.4x+,则下列选项正确的有( )
A.=1.8
B.经验回归直线=3.4x+必过点(2,9)
C.加工6个零件的时间大约为22.2 min
D.若去掉(3,12),剩下4组数据的经验回归方程不会有变化
√
√
ACD [=(5+9+12+15+19)=
12,所以经验回归直线=3.4x+恒过点(3,12),所以12=3.4×3+,解得=1.8,故A正确;
当x=2时,=3.4×2+1.8=8.6≠9,故B错误;
由=3.4x+1.8,令x=6,则=3.4×6+1.8=22.2,
故加工6个零件的时间大约为22.2 min,故C正确;
因为经验回归直线=3.4x+1.8恒过点(3,12),所以剩下4组数据的经验回归方程不会有变化,故D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
11.若实数a
B.若a>1,则logaab>2
C.若a>0,则>
D.若m>,a,b∈(1,3),则(a3-b3)-m(a2-b2)+a-b>0
√
√
BCD [对于A,当a=0时,=,所以选项A错误;对于B,
因为a>1,b>a,所以ab>a2>1,又y=logax为增函数,
所以logaab>logaa2=2,所以选项B正确;
对于C,==
=,因为a>0,b>a,所以b>a>0,b-a>0,
所以(1+a)(1+b)>0,b2+a2+ab+a+b>0,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
所以>0,即>0,即>,所以选项C正确;对于D,(a3-b3)-m(a2-b2)+a-b=a3-ma2+a-,令f (x)=x3-mx2+x,则f ′(x)=x2-2mx+1,因为m>,所以f ′(1)=2-2m<2-<0,f ′(3)=10-6m<10-6×=0,所以f ′(x)<0在(1,3)上恒成立,所以函数f (x)在(1,3)上单调递减.又1
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
三、填空题:本题共3小题,每小题5分,共15分.
12.(2024·台州期末)某学校有高二学生600人,其中男生360人,女生240人.有人为了获得该校全体高二学生的身高信息,采用分层随机抽样的方法抽取了容量为100的总样本(观测数据单位:cm),若已知男生样本的平均数为172,女生样本的平均数为162,则总样本的平均数是________.
168
168 [男生样本的平均数为172,女生样本的平均数为162,
则总样本的平均数是:×172+×162=168.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
13.某老师很喜欢“学习强国”中“挑战答题”模块,他记录了自己连续七天每天一次最多答对的题数,如下表:
天数x 1 2 3 4 5 6 7
一次最多答 对题数y 12 15 16 18 21 24 27
由表中数据可知该老师每天一次最多答对题数y与天数x之间是________相关(填“正”或“负”),其样本相关系数r≈________(结果保留两位小数).
正
0.99
参考数据:=4,=19,=140,=2 695,
xiyi=600,≈2.45,
样本相关系数r=.
正 0.99 [由表中数据知,y随x的增大而增大,
所以该老师每天一次最多答对题数y与天数x之间是正相关.
r==≈0.99.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
14.已知双曲线方程为=1(a>0,b>0),左焦点F关于一条渐
近线的对称点在另一条渐近线上,则该双曲线的离心率为_______.
2 [如图,设F关于渐近线y=x对称的点A在渐近线y=-x上,
2
FA的中点B在渐近线y=x上,
则∠FOB=∠BOA,
又∠FOB=∠AOx,
所以∠FOB=∠BOA=∠AOx=60°,
所以tan 60°==,
所以e=====2.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)每年的11月9日为“119消防宣传日”.消防宣传日的设立,旨在提醒全民关注消防安全,学习消防知识,提高自救互救能力,减少火灾事故的发生.某高中学校为增强学生的消防安全意识,组织本校高一、高二共800名学生参加“消防安全,在我心中”的知识竞赛,现从每个年级分别随机抽取10名学生的竞赛成绩如下:
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
高一:90 85 82 85 97 83 88 95 90 85
高二:83 90 97 88 95 85 95 85 80 82
(1)请根据以上20个数据,估计此次参赛学生成绩的第60百分位数、众数和平均数;
(2)若规定95分及以上为一等奖,从一等奖的学生中任选2人作为宣讲代表,则这2人中至少有1人来自高一年级的概率是多少?
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
[解] (1)把20个数据由小到大排列为80,82,82,83,83,85,85,85,85,85,88,88,90,90,90,95,95,95,97,97,由20×60%=12,
估计此次参赛学生成绩的第60百分位数为=89,
估计此次参赛学生成绩的众数为85,
平均数为=(80+82×2+83×2+85×5+88×2+90×3+95×3+
97×2)=88.
(2)成绩在95分及以上的有5人,来自高一年级的有2人,记为1,2,
来自高二年级的有3人,记为a,b,c,
从5人中任选2人的样本空间为:
Ω={12,1a,1b,1c,2a,2b,2c,ab,ac,bc},共10个样本点,
设事件A表示“这2人中至少有1人来自高一年级”,
则A={12,1a,1b,1c,2a,2b,2c},共7个样本点,
∴这2人中至少有1人来自高一年级的概率是P(A)=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
16.(15分)(2024·北京西城区模拟)每年的4月23日是联合国教科文组织确定的“世界读书日”,又称“世界图书和版权日”.A校为了了解学生的课外阅读情况,随机调查了n名学生,发现这些学生的课外日均阅读时间(单位:分钟)均在[0,120].根据这n名学生的课外日均阅读时间,将样本数据分组为:[0,20),[20,40),[40,60),[60,80),[80,100),[100,120],并绘制出如下频率分布表.
分组 频数 频率
[0,20) 4 f1
[20,40) 10 0.1
[40,60) 46 f2
[60,80) a f3
[80,100) 20 f4
[100,120] 4 f5
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(1)求n,f3的值;
(2)若采用分层随机抽样的方法从课外日均阅读时间为[60,80),[80,100),[100,120]的学生中抽取10人,再从抽取的10名学生中随机抽取1名学生进行阅读经验分享,求抽到做阅读经验分享的学生的课外日均阅读时间不少于80分钟的概率;
(3)现从这n名学生中评出课外日均阅读时间较长的10人为“阅读达人”,请算出要成为“阅读达人”至少需要的课外日均阅读时间.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
[解] (1)因为数据在[20,40)内的频数为10,频率为0.1,
所以=0.1 n=100,
则4+10+46+a+20+4=100 a=16,所以f3==0.16.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)因为课外日均阅读时间在[60,80),[80,100),[100,120]的学生比例为16∶20∶4=4∶5∶1,
所以采用分层随机抽样的方法从课外日均阅读时间为[60,80),[80,100),[100,120]的学生中抽取10人,
日均阅读时间在[60,80),[80,100),[100,120]的人数分别为4,5,1,则课外日均阅读时间不少于80分钟的人数为6人,
抽到做阅读经验分享的学生的课外日均阅读时间不少于80分钟的概
率为=0.6.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(3)这n名学生中评出课外日均阅读时间较长的10人为“阅读达人”,日均阅读时间在[100,120]的学生人数为4人,
再从日均阅读时间在[80,100)的学生中选出6个阅读时间较长的人即可,
设6个人中阅读时间最短的是x分钟,则= x=94,
所以成为“阅读达人”需要的课外日均阅读时间至少94分钟.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
17.(15分)某电商平台统计了近七年小家电的年度广告费支出xi(单位:万元)与年度销售量yi(单位:万台)的数据,如表所示:
年份 2018 2019 2020 2021 2022 2023 2024
广告费支 出x/万元 1 2 4 6 11 13 19
销售量 y/万台 1.9 3.2 4.0 4.4 5.2 5.3 5.4
其中xiyi=279.4,=708.
(1)若用线性经验回归模型拟合y与x的关系,求出y关于x的经验回归方程;
(2)若用y=c+d模型拟合得到的非线性经验回归方程为=1.63+0.99,经计算线性经验回归模型及该模型的R2分别为0.75和0.88,请根据R2的数值选择更好的经验回归模型拟合y与x的关系,进而计算出年度广告费x为何值时,利润=200y-x的预报值最大?
参考公式:==,=-.
[解] (1)由题意可得:
==8,==4.2,
所以===0.17,
==4.2-0.17×8=2.84,
所以y关于x的经验回归方程为=0.17x+2.84.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)因为0.75<0.88,R2越大,拟合效果越好,所以选用非线性经验回归方程=1.63+0.99更好,
=200(1.63+0.99)-x=-x+198+326,
=-(-99)2+10 127,
所以当=99,即x=9 801时,利润的预报值最大.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
18.(17分)如图,在多面体ABCDEF中,四边形ABCD与ABEF均为直角梯形,AD∥BC,AF∥BE,DA⊥平面ABEF,AB⊥AF,AD=AB=2BC=2BE=2.
(1)已知点G为AF上一点,且AG=2,
求证:BG与平面DCE不平行;
(2)已知直线BF与平面DCE所成角的正弦值
为,求AF的长及四棱锥D-ABEF的体积.
[解] (1)证明:因为DA⊥平面ABEF,AB,AF 平面ABEF,
所以DA⊥AB,DA⊥AF,又AB⊥AF,所以AB,AF,DA两两垂直.
以A为坐标原点,AF,AB,AD所在直线分别为x,y,z轴,建立空间直角坐标系,
则B(0,2,0),E(1,2,0),
C(0,2,1),D(0,0,2),G(2,0,0),
所以=(-1,0,1),=(-1,-2,2),
=(2,-2,0).
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
设平面DCE的法向量为n=(x,y,z),
则
令x=2,则z=2,y=1,所以n=(2,1,2)为平面DCE的一个法向量,
因为n·=2×2+1×(-2)=2≠0,
所以与n不垂直,
所以BG与平面DCE不平行.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)设AF=a(a>0且a≠1),则F (a,0,0),所以=(a,-2,0),
∵直线BF与平面DCE所成角的正弦值为,
∴==
==,
化简得11a2-40a-16=0,解得a=4或a=-(舍去),故AF=4.
此时S梯形ABEF=×(1+4)×2=5,故VD-ABEF=S梯形ABEF·DA=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
19.(17分)(2024·嘉兴二模)春季流感对广大民众的健康生活带来一定的影响,为了有效预防流感,很多民众注射了流感疫苗.某市防疫部门从辖区居民中随机抽取了1 000人进行调查,发现其中注射疫苗的800人中有220人感染流感,另外没注射疫苗的200人中有80人感染流感.医学研究表明,流感的检测结果有错检的可能,已知患有流感的人其检
测结果有95%呈阳性(感染),而没有患流感的人其检测结果有99%呈阴性(未感染).
(1)估计该市流感感染率是多少?
(2)依据小概率值α=0.001的独立性检验,能否认为注射流感疫苗与预防流感有关?
(3)已知某人的流感检测结果呈阳性,求此人真的患有流感的概率.(精确到0.001)
附:χ2=,
α 0.1 0.05 0.01 0.005 0.001
xα 2.706 3.841 6.635 7.879 10.828
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
[解] (1)估计流感的感染率P==0.3.
(2)根据题意,得到2×2列联表如下:
单位:人
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
疫苗 流感 合计
患流感 不患流感
打疫苗 220 580 800
不打疫苗 80 120 200
合计 300 700 1 000
零假设为
H0:注射流感疫苗与预防流感无关.
χ2==≈11.905,
因为11.905>10.828,
所以依据小概率值α=0.001的独立性检验,推断H0不成立,即认为注射流感疫苗与预防流感有关.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(3)设事件A为“一次检测结果呈阳性”,事件B为“被检测者确实患有流感”,
由题意得P(B)=0.3,P()=0.01,
由全概率公式得P(A)=P(B)·P(A|B)+P()=0.3×0.95+0.7×0.01=0.292,
所以P(B|A)===≈97.6%,
即此人真的患有流感的概率是97.6%.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
谢 谢 !
同课章节目录
