《高考快车道》2026版高三一轮总复习数学(基础版)118 2026年普通高等学校招生全国统一考试仿真卷(一) 课件
文档属性
| 名称 | 《高考快车道》2026版高三一轮总复习数学(基础版)118 2026年普通高等学校招生全国统一考试仿真卷(一) 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 13:54:09 | ||
图片预览











文档简介
(共49张PPT)
2026年普通高等学校招生全国统一考试仿真卷(一)
单元检测(一)
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A=[0,a],B=(2,3),若A∩B= ,则( )
A.0<a≤2 B.0<a<2
C.0<a<3 D.0<a≤3
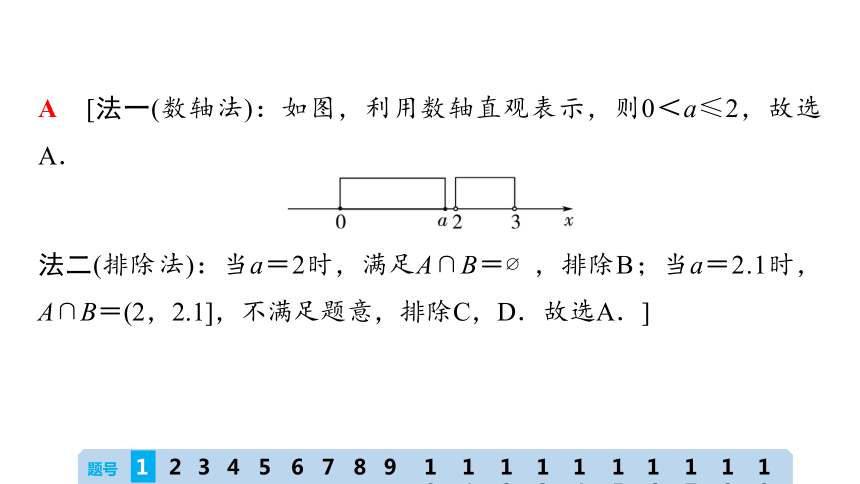
A [法一(数轴法):如图,利用数轴直观表示,则0<a≤2,故选A.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二(排除法):当a=2时,满足A∩B= ,排除B;当a=2.1时,A∩B=(2,2.1],不满足题意,排除C,D.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
2.设z=,则=( )
A.i B.-i
C.+i D.-i
A [因为z==-i,所以=i.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
3.(1-x)6的展开式中,x2的系数为( )
A.-5 B.5
C.15 D.35
A [(1-x)6的展开式的通项为Tk+1=,令k=2,得T3=x2,令k=3,得T4=-x3,所以(1-x)6的展开式中,x2的系数为+1×=-5.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
4.等差数列{an}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{an}的前5项和为( )
A.-15 B.-3 C.5 D.25
A [设等差数列{an}的公差为d,则d≠0,a2=1+d,a3=1+2d,a6=1+5d.由题意可知,(1+2d)2=(1+d)(1+5d),得d2=-2d,解得d=-2或d=0(舍去).记数列{an}的前n项和为Sn,则S5=5a1+d=5-20=-15.故选A.]
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
5.下列命题为真命题的是( )
A.若a>b,则>
B.若a>b,c>d,则a-d>b-c
C.若a<b<0,则a2<ab<b2
D.若a>b,则>
B [对于A,取a=2,b=1,满足a>b,当c=-1时,<,所以
A是假命题;对于B,若c>d,则-d>-c,又a>b,所以a-d>b-c,故B是真命题;对于C,取a=-2,b=-1,满足ab=-1,满足a>b,则<,故D是假命题.
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
6.两台车床加工同样的零件,第一台出现废品的概率为0.03,第二台出现废品的概率为0.02,加工出来的零件放在一起,现已知第一台加工的零件比第二台加工的零件多一倍,则任意取出一个零件是合格品的概率是( )
A. B.
C. D.
B [记事件A1为取出的一个零件是第一台车床加工的,事件A2为取出的一个零件是第二台车床加工的,事件B为取出的一个零件是合
格品,则P(A1)=,P(A2)=,,,P(A1)+P(B|A2)P(A2)=0.97×+0.98×.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
7.已知角α,β满足tan α=,2sin β=cos (α+β)sin α,则tan β=( )
A. B.
C. D.2
C [法一(利用同角三角函数的基本关系求解):由tan α=,得cos α=3sin α,①
又sin2α+cos2α=1,②
所以由①②得,sin2α=,所以cos(α+β)sin α=(cos αcos β-
sin αsin β)sin α=(3sin αcos β-sin αsin β)sin α=(3cos β-sin β)sin2α=(3cosβ-sin β)=2sin β,整理得,7sin β=cos β,所以tan β=.故选C.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二(凑角法):因为β=(α+β)-α,2sin β=cos (α+β)sin α,所以2sin[(α+β)-α]=cos (α+β)sin α,即2[sin (α+β)cos α-
cos (α+β)sin α]=cos (α+β)sin α,整理得2sin (α+β)cos α=3cos (α+
β)sin α,即tan (α+β)=tan α=,所以tan β=tan [(α+β)-α]=.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
8.已知双曲线C:=1(a>0,b>0)的右焦点为F,一条渐近线的方程为y=2x,直线y=kx与C在第一象限内的交点为P.若|PF|=|PO|,则k的值为( )
A. B.
C. D.
C [由题意知,双曲线C的渐近线方程为y=x.因为双曲线C的一条渐近线的方程是y=2x,所以b=2a.如图,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
设点P的坐标为(x1,y1),右焦点F (c,0),则c=a.由|PF|=
,解得x1=.将x1=代入双曲线C的方程,得=1,则=1,y=±a,即y1=±a.因为点P在第一象限内,所以P.因为点P在直线y=kx上,所以a=k×,解得k=.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知m,n是两条不同的直线,α,β是两个不同的平面,以下四个命题正确的是( )
A.若m∥n,n α,则m∥α
B.若m α,m⊥β,则α⊥β
C.若m⊥α,m⊥β,则α∥β
D.若α⊥β,m β,n α,则m⊥n
√
BC [当m∥n,n α时,m∥α或m α,所以A错误;当m α,m⊥β时,由面面垂直的判定定理可得α⊥β,所以B正确;当m⊥α,m⊥β时,有α∥β,所以C正确;当α⊥β,m β,n α时,如图所示,m∥n,所以D错误.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
10.已知函数f (x)=ax3+bx2+cx+d(a≠0),若y=|f (x)-2|的图象关于直线x=1对称,则下列说法正确的是( )
A.y=|f (x)|的图象也关于直线x=1对称
B.y=f (x)的图象关于(1,2)中心对称
C.a+b+c+d=2
D.3a+b=0
√
√
BCD [法一:因为函数y=|f (x)-2|的图象关于直线x=1对称,所以|f (1+x)-2|=|f (1-x)-2|,即f (1+x)-2=f (1-x)-2或f (1+x)-2=2-f (1-x).当f (1+x)-2=f (1-x)-2时,f (1+x)=f (1-x),即函数f (x)的图象关于直线x=1对称,又函数f (x)=ax3+bx2+cx+d(a≠0)的图象是中心对称图形,不是轴对称图形,所以f (1+x)≠f (1-x);当f (1+x)-2=2-f (1-x)时,f (1+x)+f (1-x)=4,所以函数f (x)的图象关于点(1,2)对称,所以f (1)=2,-=1,即a+b+c+d=2,3a+b=0,所以B,C,D均正确.若函数y=|f (x)|的图象关于直线x=1对称,则有|f (1-x)|=|f (1+x)|,又函数f (x)的图象是中心对称图形,所以f (1+x)+f (1-x)=0,即f (x)的图象关于(1,0)对称,与函数f (x)的图象关于点(1,2)对称矛盾,所以A错误.综上,选BCD.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二(数形结合法):因为三次函数的图象为中心对称图形,所以要使|f (x)-2|的图象关于直线x=1对称,则f (x)的图象的对称中心的横坐标也为1,且f (x)-2的图象关于(1,0)对称,所以f (x)的图象关于(1,2)对称,且|f (x)|的图象不关于直线x=1对称,所以A错误,B正
确.由f (x)的图象关于(1,2)对称可得所以a+b+c+d=
2,3a+b=0,故C,D正确.故选BCD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
11.已知直线l:ax+by+1=0(a,b不同时为0),圆C:x2+y2-2x=0,则下列说法正确的是( )
A.当b2-2a=1时,直线l与圆C相切
B.当a+b=-2时,直线l与圆C不可能相交
C.当a=1,b=-1时,与圆C外切且与直线l相切的动圆圆心的轨迹是一条抛物线
D.当a=1,b=-1时,直线l与坐标轴相交于A,B两点,则圆C上存在点P满足=0
√
√
ACD [圆C:x2+y2-2x=0即(x-1)2+y2=1,其圆心为C(1,0),半径r=1.
对于A,若b2-2a=1,则圆心C到直线l的距离d==1=r,所以直线l与圆C相切,故A正确;
对于B,当a=0,b=-2时,满足a+b=-2,此时直线l的方程为y
=,圆心C到直线l的距离为题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
对于C,当a=1,b=-1时,直线l:x-y+1=0,此时直线x-y+1
+=0与直线l平行,且两平行线间的距离d1==1,如
图,结合题意可知,动圆圆心到直线x-y+1+=0的距离与到C(1,0)的距离相等,显然点C(1,0)不在直线x-y+1+=0上,根据抛物线的定义可知动圆圆心的轨迹是一条抛物线,故C正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
对于D,不妨令A(-1,0),B(0,1),记AB的中点为D=,所以以AB为直径的圆的方程为=<+
1,所以圆D与圆C相交,所以圆C上存在点P满足=0,故D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量a,b满足|a|=2,(4a+b)·b=4,则|2a+b|=________.
2 [∵(4a+b)·b=4,∴4a·b+b2=4,又|a|=2,
所以|2a+b|=.]
2
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
13.为了解全市高三学生的体能素质情况,在全市高三学生中随机抽取了1 000名学生进行体能测试,并将这1 000名学生的体能测试成绩(单位:分)整理成如图所示的频率分布直方图.则频率分布直方图中实数a的值为________.
0.015
0.015 [由题图中频率分布直方图可得10×(0.005+a+0.020+0.040+0.020)=1,
解得a=0.015.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
14.已知△ABC中,点D在边AC上,∠ABC=60°,sin A=3sin C,AC=,则△ABC的面积为________;若,则BD=________.
[令BC=a,AC=b,AB=c,由正弦定理及sin A=
3sin C,得a=3c,由余弦定理得b2=a2+c2-2ac cos ∠ABC=a2+c2
-ac=7,所以c=1,a=3,所以S△ABC=ac sin ∠ABC=.
法一:因为,所以,所以BD2=|2 +2=,得BD=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二:cos A=.因为,所以AD=.在△ABD中,由余弦定理得BD2=AB2+AD2-2AB×AD×cos A=,所以BD=.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)在△ABC中,角A,B,C所对的边分别为a,b,c,c=4,ab=9.
(1)若sin C=,求sin A·sin B的值;
(2)求△ABC面积的最大值.
[解] (1)∵=6,∴sin A=,sin B=,
∴sin A·sin B=.
(2)∵ab=9,∴a2+b2≥2ab=18,当且仅当a=b=3时等号成立,
∴cos C=,又C∈(0,π),∴≤cos C<1,
∴0<1-cos2C≤,∴0sin C≤2,∴△ABC面积的最大值为2.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
16.(15分)如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD中,∠ABC=90°,AB∥CD,AB=1,BC=1,CD=2,点A在平面PCD内的射影恰好是△PCD的重心G.
(1)证明:平面PAB⊥平面PBC;
(2)求直线DG与平面PBC所成角的正弦值.
[解] (1)证明:因为PA⊥平面ABCD,BC 平面ABCD,所以PA⊥BC.
因为∠ABC=90°,所以BC⊥AB.
因为PA∩AB=A,PA 平面PAB,AB 平面PAB,
所以BC⊥平面PAB.
又BC 平面PBC,所以平面PAB⊥平面PBC.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)如图,取CD的中点E,连接AE.
因为∠ABC=90°,AB∥CD,AB=BC=1,CD=2,
所以四边形ABCE是矩形,所以AB⊥AE,AE=BC=1.
因为PA⊥平面ABCD,所以PA⊥AB,PA⊥AE,
所以直线AB,AE,AP两两垂直,
建立如图所示的空间直角坐标系,
则A(0,0,0),B(1,0,0),C(1,1,0),D(-1,1,0),
所以=(0,1,0).
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
连接PE,因为G为△PCD的重心,所以点G在线段PE上,且PE=3EG.
设P(0,0,t)(t>0),则G,
.
因为点A在平面PCD内的射影恰好是△PCD的重心G,所以AG⊥平面PCD,又DG 平面PCD,所以AG⊥DG,
所以=0,所以0-=0,得t=,所以P,所以=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
设m=(x,y,z)是平面PBC的法向量,
则即
令z=1,得m=为平面PBC的一个法向量.
设直线DG与平面PBC所成的角为θ,
则sin θ==,
即直线DG与平面PBC所成角的正弦值为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
17.(15分)春夏之交因昼夜温差大,细菌、病毒等活跃,是流感高发季节.某校高二年级某组团统计了流感发生前的半个月与发生后的半个月的学生请假情况,得到如下数据:
单位:人
流感 请假 合计
因发烧请假 非发烧请假
发生前 10 30
发生后 30
合计 70
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(1)完成2×2列联表,并依据小概率值α=0.001的独立性检验,判断能否认为流感发生对请假的同学中发烧的人数有影响;
(2)后经过了解,在全校因发烧请假的同学中男生占比为40%,且20%的因发烧请假的男生需要输液治疗,30%的因发烧请假的女生需要输液治疗.学校随机选择一名因发烧请假在医院输液的同学进行慰问,求这名同学是女生的概率.
附:χ2=.
α 0.05 0.01 0.001
xα 3.841 6.635 10.828
[解] (1)2×2列联表如下:
单位:人
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
流感 请假 合计
因发烧请假 非发烧请假
发生前 10 20 30
发生后 30 10 40
合计 40 30 70
零假设为
H0:流感发生与请假的同学中发烧的人数之间相互独立,
因为χ2=≈12.153>10.828,
所以依据小概率值α=0.001的独立性检验,我们推断H0不成立,即可以认为流感发生对请假的同学中发烧的人数有影响.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)设A事件表示请假的同学为女生,B事件表示需要输液治疗,
则P(A|B)==,
所以这名同学是女生的概率为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
18.(17分)已知函数f (x)=ex-1-a(其中a∈R),g(x)=ln x.
(1)当a=0时,求函数f (x)的图象在点(0,f (0))处的切线方程;
(2)当x>0时,若f (x)≥g(x)恒成立,求a的取值范围.
[解] (1)当a=0时,f (x)=ex-1,f (0)=e-1=,f ′(x)=ex-1,f ′(0)=e-1=,故函数f (x)的图象在点(0,f (0))处的切线方程为y-x,
即x-ey+1=0.
(2)当x>0时,ex-1-a≥ln x恒成立,即ex-1-ln x≥a恒成立,
令t(x)=ex-1-ln x,x∈(0,+∞),则t′(x)=ex-1-,
令w(x)=t′(x)=ex-1-,x∈(0,+∞),则w′(x)=ex-1+>0在(0,
+∞)上恒成立,故w(x)=t′(x)=ex-1-在(0,+∞)上单调递增,
又t′(1)=e1-1-1=0,故当x∈(0,1)时,t′(x)<0,当x∈(1,+∞)时,t′(x)>0,故t(x)=ex-1-ln x在(0,1)上单调递减,在(1,+∞)上单调递增,t(x)min=e1-1-ln 1=1,所以a的取值范围是(-∞,1].
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
19.(17分)已知双曲线C:=1(a>0,b>0)的左、右顶点分别
为A与B,点D在C上,且直线AD与BD的斜率之和为.
(1)求双曲线C的方程;
(2)过点P(3,0)的直线与C交于M,N两点(均异于点A,B),直线MA与直线x=1交于点Q,求证:B,N,Q三点共线.
[解] (1)由题意得A(-a,0),B(a,0),
则∴
∴双曲线C的方程为-y2=1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)证明:由(1)得A,B,易知直线MN的斜率不为0,故设直线MN的方程为x=ty+3,M(x1,y1),N(x2,y2),则=,
由消去x得(t2-3)y2+6ty+6=0,
Δ=12t2+72>0,∴y1+y2=-.
易知直线AM的方程为y=,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
令x=1,则y=,∴Q,
∴,∵·-y2=·[·y1-]=·y1-·]=·y1+]=(ty1y2+y1+y2)==0,
∴∥,∴B,N,Q三点共线.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
谢 谢 !
2026年普通高等学校招生全国统一考试仿真卷(一)
单元检测(一)
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A=[0,a],B=(2,3),若A∩B= ,则( )
A.0<a≤2 B.0<a<2
C.0<a<3 D.0<a≤3
A [法一(数轴法):如图,利用数轴直观表示,则0<a≤2,故选A.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二(排除法):当a=2时,满足A∩B= ,排除B;当a=2.1时,A∩B=(2,2.1],不满足题意,排除C,D.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
2.设z=,则=( )
A.i B.-i
C.+i D.-i
A [因为z==-i,所以=i.故选A.]
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
3.(1-x)6的展开式中,x2的系数为( )
A.-5 B.5
C.15 D.35
A [(1-x)6的展开式的通项为Tk+1=,令k=2,得T3=x2,令k=3,得T4=-x3,所以(1-x)6的展开式中,x2的系数为+1×=-5.故选A.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
4.等差数列{an}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{an}的前5项和为( )
A.-15 B.-3 C.5 D.25
A [设等差数列{an}的公差为d,则d≠0,a2=1+d,a3=1+2d,a6=1+5d.由题意可知,(1+2d)2=(1+d)(1+5d),得d2=-2d,解得d=-2或d=0(舍去).记数列{an}的前n项和为Sn,则S5=5a1+d=5-20=-15.故选A.]
√
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
5.下列命题为真命题的是( )
A.若a>b,则>
B.若a>b,c>d,则a-d>b-c
C.若a<b<0,则a2<ab<b2
D.若a>b,则>
B [对于A,取a=2,b=1,满足a>b,当c=-1时,<,所以
A是假命题;对于B,若c>d,则-d>-c,又a>b,所以a-d>b-c,故B是真命题;对于C,取a=-2,b=-1,满足a
故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
6.两台车床加工同样的零件,第一台出现废品的概率为0.03,第二台出现废品的概率为0.02,加工出来的零件放在一起,现已知第一台加工的零件比第二台加工的零件多一倍,则任意取出一个零件是合格品的概率是( )
A. B.
C. D.
B [记事件A1为取出的一个零件是第一台车床加工的,事件A2为取出的一个零件是第二台车床加工的,事件B为取出的一个零件是合
格品,则P(A1)=,P(A2)=,,,P(A1)+P(B|A2)P(A2)=0.97×+0.98×.故选B.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
7.已知角α,β满足tan α=,2sin β=cos (α+β)sin α,则tan β=( )
A. B.
C. D.2
C [法一(利用同角三角函数的基本关系求解):由tan α=,得cos α=3sin α,①
又sin2α+cos2α=1,②
所以由①②得,sin2α=,所以cos(α+β)sin α=(cos αcos β-
sin αsin β)sin α=(3sin αcos β-sin αsin β)sin α=(3cos β-sin β)sin2α=(3cosβ-sin β)=2sin β,整理得,7sin β=cos β,所以tan β=.故选C.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二(凑角法):因为β=(α+β)-α,2sin β=cos (α+β)sin α,所以2sin[(α+β)-α]=cos (α+β)sin α,即2[sin (α+β)cos α-
cos (α+β)sin α]=cos (α+β)sin α,整理得2sin (α+β)cos α=3cos (α+
β)sin α,即tan (α+β)=tan α=,所以tan β=tan [(α+β)-α]=.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
8.已知双曲线C:=1(a>0,b>0)的右焦点为F,一条渐近线的方程为y=2x,直线y=kx与C在第一象限内的交点为P.若|PF|=|PO|,则k的值为( )
A. B.
C. D.
C [由题意知,双曲线C的渐近线方程为y=x.因为双曲线C的一条渐近线的方程是y=2x,所以b=2a.如图,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
设点P的坐标为(x1,y1),右焦点F (c,0),则c=a.由|PF|=
,解得x1=.将x1=代入双曲线C的方程,得=1,则=1,y=±a,即y1=±a.因为点P在第一象限内,所以P.因为点P在直线y=kx上,所以a=k×,解得k=.故选C.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知m,n是两条不同的直线,α,β是两个不同的平面,以下四个命题正确的是( )
A.若m∥n,n α,则m∥α
B.若m α,m⊥β,则α⊥β
C.若m⊥α,m⊥β,则α∥β
D.若α⊥β,m β,n α,则m⊥n
√
BC [当m∥n,n α时,m∥α或m α,所以A错误;当m α,m⊥β时,由面面垂直的判定定理可得α⊥β,所以B正确;当m⊥α,m⊥β时,有α∥β,所以C正确;当α⊥β,m β,n α时,如图所示,m∥n,所以D错误.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
10.已知函数f (x)=ax3+bx2+cx+d(a≠0),若y=|f (x)-2|的图象关于直线x=1对称,则下列说法正确的是( )
A.y=|f (x)|的图象也关于直线x=1对称
B.y=f (x)的图象关于(1,2)中心对称
C.a+b+c+d=2
D.3a+b=0
√
√
BCD [法一:因为函数y=|f (x)-2|的图象关于直线x=1对称,所以|f (1+x)-2|=|f (1-x)-2|,即f (1+x)-2=f (1-x)-2或f (1+x)-2=2-f (1-x).当f (1+x)-2=f (1-x)-2时,f (1+x)=f (1-x),即函数f (x)的图象关于直线x=1对称,又函数f (x)=ax3+bx2+cx+d(a≠0)的图象是中心对称图形,不是轴对称图形,所以f (1+x)≠f (1-x);当f (1+x)-2=2-f (1-x)时,f (1+x)+f (1-x)=4,所以函数f (x)的图象关于点(1,2)对称,所以f (1)=2,-=1,即a+b+c+d=2,3a+b=0,所以B,C,D均正确.若函数y=|f (x)|的图象关于直线x=1对称,则有|f (1-x)|=|f (1+x)|,又函数f (x)的图象是中心对称图形,所以f (1+x)+f (1-x)=0,即f (x)的图象关于(1,0)对称,与函数f (x)的图象关于点(1,2)对称矛盾,所以A错误.综上,选BCD.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二(数形结合法):因为三次函数的图象为中心对称图形,所以要使|f (x)-2|的图象关于直线x=1对称,则f (x)的图象的对称中心的横坐标也为1,且f (x)-2的图象关于(1,0)对称,所以f (x)的图象关于(1,2)对称,且|f (x)|的图象不关于直线x=1对称,所以A错误,B正
确.由f (x)的图象关于(1,2)对称可得所以a+b+c+d=
2,3a+b=0,故C,D正确.故选BCD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
√
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
11.已知直线l:ax+by+1=0(a,b不同时为0),圆C:x2+y2-2x=0,则下列说法正确的是( )
A.当b2-2a=1时,直线l与圆C相切
B.当a+b=-2时,直线l与圆C不可能相交
C.当a=1,b=-1时,与圆C外切且与直线l相切的动圆圆心的轨迹是一条抛物线
D.当a=1,b=-1时,直线l与坐标轴相交于A,B两点,则圆C上存在点P满足=0
√
√
ACD [圆C:x2+y2-2x=0即(x-1)2+y2=1,其圆心为C(1,0),半径r=1.
对于A,若b2-2a=1,则圆心C到直线l的距离d==1=r,所以直线l与圆C相切,故A正确;
对于B,当a=0,b=-2时,满足a+b=-2,此时直线l的方程为y
=,圆心C到直线l的距离为
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
对于C,当a=1,b=-1时,直线l:x-y+1=0,此时直线x-y+1
+=0与直线l平行,且两平行线间的距离d1==1,如
图,结合题意可知,动圆圆心到直线x-y+1+=0的距离与到C(1,0)的距离相等,显然点C(1,0)不在直线x-y+1+=0上,根据抛物线的定义可知动圆圆心的轨迹是一条抛物线,故C正确;
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
对于D,不妨令A(-1,0),B(0,1),记AB的中点为D=,所以以AB为直径的圆的方程为=<+
1,所以圆D与圆C相交,所以圆C上存在点P满足=0,故D正确.故选ACD.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
三、填空题:本题共3小题,每小题5分,共15分.
12.已知向量a,b满足|a|=2,(4a+b)·b=4,则|2a+b|=________.
2 [∵(4a+b)·b=4,∴4a·b+b2=4,又|a|=2,
所以|2a+b|=.]
2
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
13.为了解全市高三学生的体能素质情况,在全市高三学生中随机抽取了1 000名学生进行体能测试,并将这1 000名学生的体能测试成绩(单位:分)整理成如图所示的频率分布直方图.则频率分布直方图中实数a的值为________.
0.015
0.015 [由题图中频率分布直方图可得10×(0.005+a+0.020+0.040+0.020)=1,
解得a=0.015.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
14.已知△ABC中,点D在边AC上,∠ABC=60°,sin A=3sin C,AC=,则△ABC的面积为________;若,则BD=________.
[令BC=a,AC=b,AB=c,由正弦定理及sin A=
3sin C,得a=3c,由余弦定理得b2=a2+c2-2ac cos ∠ABC=a2+c2
-ac=7,所以c=1,a=3,所以S△ABC=ac sin ∠ABC=.
法一:因为,所以,所以BD2=|2 +2=,得BD=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
法二:cos A=.因为,所以AD=.在△ABD中,由余弦定理得BD2=AB2+AD2-2AB×AD×cos A=,所以BD=.]
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)在△ABC中,角A,B,C所对的边分别为a,b,c,c=4,ab=9.
(1)若sin C=,求sin A·sin B的值;
(2)求△ABC面积的最大值.
[解] (1)∵=6,∴sin A=,sin B=,
∴sin A·sin B=.
(2)∵ab=9,∴a2+b2≥2ab=18,当且仅当a=b=3时等号成立,
∴cos C=,又C∈(0,π),∴≤cos C<1,
∴0<1-cos2C≤,∴0
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
16.(15分)如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD中,∠ABC=90°,AB∥CD,AB=1,BC=1,CD=2,点A在平面PCD内的射影恰好是△PCD的重心G.
(1)证明:平面PAB⊥平面PBC;
(2)求直线DG与平面PBC所成角的正弦值.
[解] (1)证明:因为PA⊥平面ABCD,BC 平面ABCD,所以PA⊥BC.
因为∠ABC=90°,所以BC⊥AB.
因为PA∩AB=A,PA 平面PAB,AB 平面PAB,
所以BC⊥平面PAB.
又BC 平面PBC,所以平面PAB⊥平面PBC.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)如图,取CD的中点E,连接AE.
因为∠ABC=90°,AB∥CD,AB=BC=1,CD=2,
所以四边形ABCE是矩形,所以AB⊥AE,AE=BC=1.
因为PA⊥平面ABCD,所以PA⊥AB,PA⊥AE,
所以直线AB,AE,AP两两垂直,
建立如图所示的空间直角坐标系,
则A(0,0,0),B(1,0,0),C(1,1,0),D(-1,1,0),
所以=(0,1,0).
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
连接PE,因为G为△PCD的重心,所以点G在线段PE上,且PE=3EG.
设P(0,0,t)(t>0),则G,
.
因为点A在平面PCD内的射影恰好是△PCD的重心G,所以AG⊥平面PCD,又DG 平面PCD,所以AG⊥DG,
所以=0,所以0-=0,得t=,所以P,所以=.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
设m=(x,y,z)是平面PBC的法向量,
则即
令z=1,得m=为平面PBC的一个法向量.
设直线DG与平面PBC所成的角为θ,
则sin θ==,
即直线DG与平面PBC所成角的正弦值为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
17.(15分)春夏之交因昼夜温差大,细菌、病毒等活跃,是流感高发季节.某校高二年级某组团统计了流感发生前的半个月与发生后的半个月的学生请假情况,得到如下数据:
单位:人
流感 请假 合计
因发烧请假 非发烧请假
发生前 10 30
发生后 30
合计 70
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(1)完成2×2列联表,并依据小概率值α=0.001的独立性检验,判断能否认为流感发生对请假的同学中发烧的人数有影响;
(2)后经过了解,在全校因发烧请假的同学中男生占比为40%,且20%的因发烧请假的男生需要输液治疗,30%的因发烧请假的女生需要输液治疗.学校随机选择一名因发烧请假在医院输液的同学进行慰问,求这名同学是女生的概率.
附:χ2=.
α 0.05 0.01 0.001
xα 3.841 6.635 10.828
[解] (1)2×2列联表如下:
单位:人
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
流感 请假 合计
因发烧请假 非发烧请假
发生前 10 20 30
发生后 30 10 40
合计 40 30 70
零假设为
H0:流感发生与请假的同学中发烧的人数之间相互独立,
因为χ2=≈12.153>10.828,
所以依据小概率值α=0.001的独立性检验,我们推断H0不成立,即可以认为流感发生对请假的同学中发烧的人数有影响.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)设A事件表示请假的同学为女生,B事件表示需要输液治疗,
则P(A|B)==,
所以这名同学是女生的概率为.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
18.(17分)已知函数f (x)=ex-1-a(其中a∈R),g(x)=ln x.
(1)当a=0时,求函数f (x)的图象在点(0,f (0))处的切线方程;
(2)当x>0时,若f (x)≥g(x)恒成立,求a的取值范围.
[解] (1)当a=0时,f (x)=ex-1,f (0)=e-1=,f ′(x)=ex-1,f ′(0)=e-1=,故函数f (x)的图象在点(0,f (0))处的切线方程为y-x,
即x-ey+1=0.
(2)当x>0时,ex-1-a≥ln x恒成立,即ex-1-ln x≥a恒成立,
令t(x)=ex-1-ln x,x∈(0,+∞),则t′(x)=ex-1-,
令w(x)=t′(x)=ex-1-,x∈(0,+∞),则w′(x)=ex-1+>0在(0,
+∞)上恒成立,故w(x)=t′(x)=ex-1-在(0,+∞)上单调递增,
又t′(1)=e1-1-1=0,故当x∈(0,1)时,t′(x)<0,当x∈(1,+∞)时,t′(x)>0,故t(x)=ex-1-ln x在(0,1)上单调递减,在(1,+∞)上单调递增,t(x)min=e1-1-ln 1=1,所以a的取值范围是(-∞,1].
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
19.(17分)已知双曲线C:=1(a>0,b>0)的左、右顶点分别
为A与B,点D在C上,且直线AD与BD的斜率之和为.
(1)求双曲线C的方程;
(2)过点P(3,0)的直线与C交于M,N两点(均异于点A,B),直线MA与直线x=1交于点Q,求证:B,N,Q三点共线.
[解] (1)由题意得A(-a,0),B(a,0),
则∴
∴双曲线C的方程为-y2=1.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
(2)证明:由(1)得A,B,易知直线MN的斜率不为0,故设直线MN的方程为x=ty+3,M(x1,y1),N(x2,y2),则=,
由消去x得(t2-3)y2+6ty+6=0,
Δ=12t2+72>0,∴y1+y2=-.
易知直线AM的方程为y=,
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
令x=1,则y=,∴Q,
∴,∵·-y2=·[·y1-]=·y1-·]=·y1+]=(ty1y2+y1+y2)==0,
∴∥,∴B,N,Q三点共线.
题号
1
3
5
2
4
6
8
7
9
10
11
12
13
14
15
16
17
18
19
谢 谢 !
同课章节目录
