人教版七年级数学下册 课件:第六章6.3实数 (共62张PPT)
文档属性
| 名称 | 人教版七年级数学下册 课件:第六章6.3实数 (共62张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-04 15:02:03 | ||
图片预览








文档简介
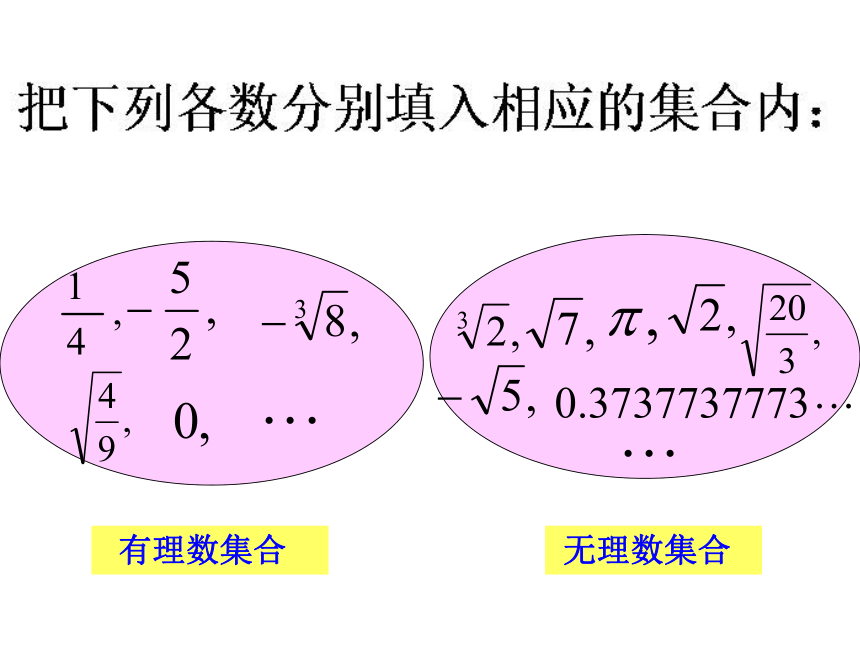
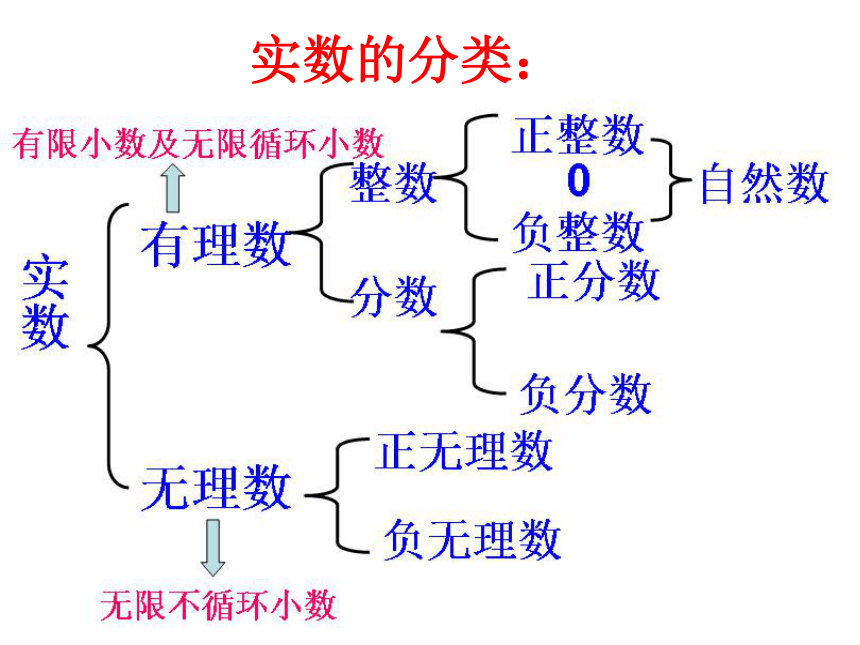
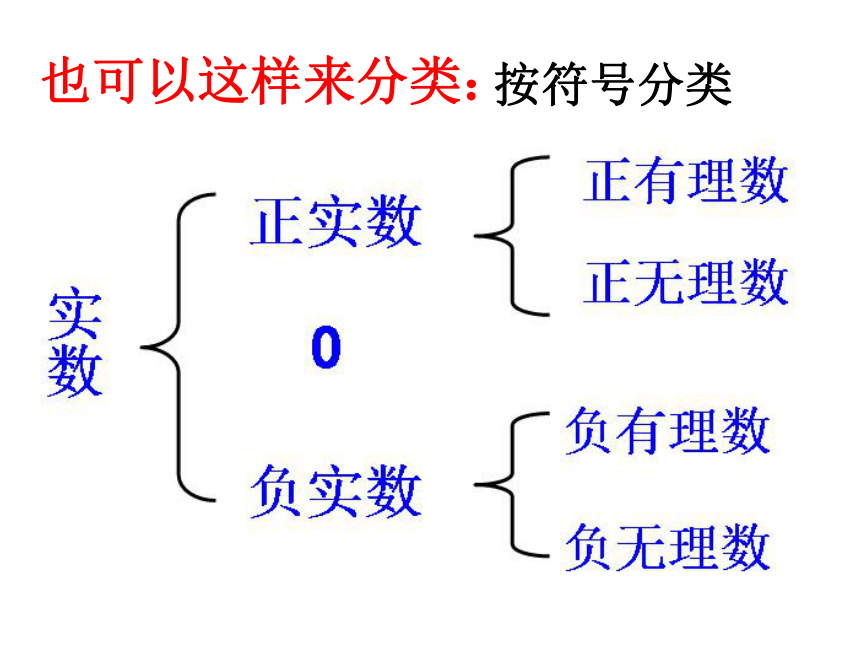
6.3 实 数 把下列各数写成小数的形式,你有什么发现? 事实上,任何一个有理数都可以写成有限小数或无限循环小数。 反过来,任何有限小数或无限循环小数也都是有理数。 除了有限小数和无限循环小数,还有什么其它类型的小数吗?无限不循环的小数---叫做无理数。有理数和无理数统称实数。 有理数集合 无理数集合实数的分类:也可以这样来分类:按符号分类一、判断:1.实数不是有理数就是无理数。( )分 析:一、判断:2.无理数都是无限不循环小数。( )分析:由定义 无限不循环的小数---叫做无理数。
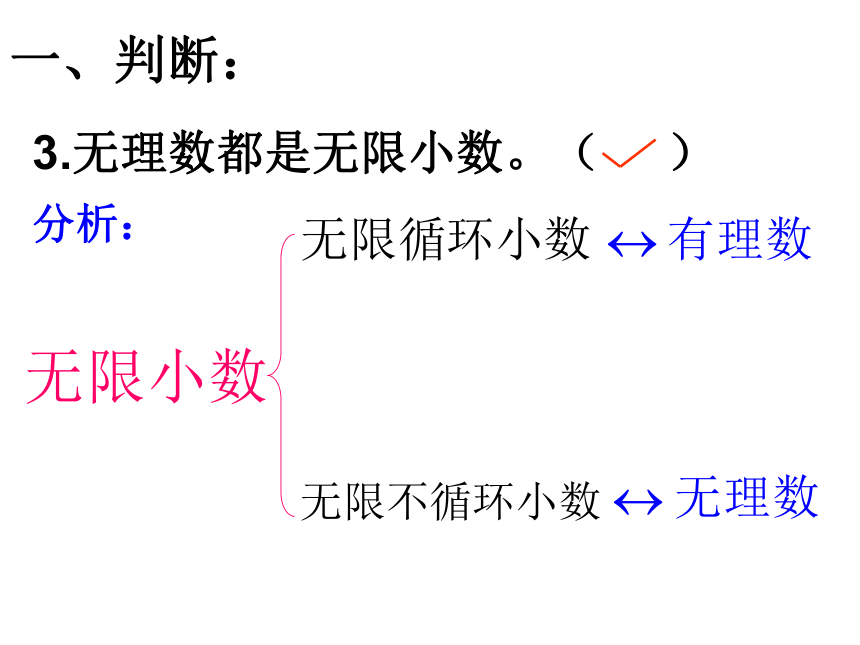
肯定正确,反过来也是正确的。一、判断:3.无理数都是无限小数。( )分析:第二课时 每个有理数都可以用数轴上的点表示,那么无理数是否也可以用数轴上的点来表示呢? 直径为1个单位长度的圆从原点沿数轴向右滚动一周.
圆上的一点由原点到达点O,点O\' 对应的数是多少?π直径为 1 的圆:公式:圆的周长=π×直径 能否用两个面积为1的小正方形拼成一个面积为2的大正方形?小正方形对角线用 表示。问题:已知大正方形的面积是2,
那么大正方形的边长是多少呢?x 2 = 2解:设大正方形的边长为x,
由题意得:
小正方形的对角线的长是多少呢?x =问题: 边长为 1 的正方形,对角线长为 也就是说:每一个无理数都可以用数轴上的一个点来表示.
但是数轴上的点:有些表示有理数,有些表示无理数.2.判断:
①一个实数不是有理数就是无理数;
②最小的实数是0;
③任何一个无理数都可以
用数轴上的点表示;
④两个无理数之和一定是无理数.
√×√×⑤数轴上的点都表示的是无理数。× 当数的范围,从有理数的基础上,添加无理数之后,第六章所指的数,全部默认为实数。
当然,从有理数的范围扩大到实数后,实数与数轴上的点是一一对应关系。DA.原点左侧
B.原点右侧
C.原点或原点左侧
D.原点或原点右侧已知:求:x的值。 ∵算术平方根的被开方数≥0,
∴ 1 – x ≥0 且 x - 1 ≥0
∴ x = 1解:② 化 简:第三课时 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。(2)如果a≠0,那么它的倒数为 。(1)a是一个实数,它的相反数 ,
绝对值为 ;相反数绝对值把课本上的三种情况,合并为两种情况。分析:①先把绝对值表示出来:②属于第几种情况?解:原式=解:原式解:原式解:原式化简求值:分析:是负数是正数是负数等于它的相反数等于本身等于它的相反数原式=( ) ( ) ( )第三课时已知:实数a、b、c,在数轴上的
位置如下图所示,试化简:
注意:去绝对值要看,
绝对值里面式子的符号。分析:①把这两个数的形式要统一起来②是写成带根号的形式?
还是整数的形式?写成根号的形式写成整数的形式第四课时 混合运算的运算顺序 :
① 从高到低:先算乘方、 开方,
再算乘除,最后算加减;
②同级运算,按照从左至右的顺序进行;
③从大大小:如果有括号,先算小括号
里的,再算中括号里的,最后算大括
号里的. 1、二次根式的加减:
同整式的加减类似:先把各个二次根式化成最简二次根式,再把同类二次根式分别合并。二次根式的加减乘除运算乘法分配律:2、二次根式相乘的法则:
两个二次根式相乘,被开方数相乘,根指数不变。二次根式的加减乘除运算3、二次根式相除的法则:
两个二次根式相除,被开方数相除,根指数不变。二次根式的加减乘除运算例:计算下列各式的值解:原式=解:原式=例:计算(结果保留小数点后两位)原式注意:计算过程中要多保留一位!例:计算(结果保留小数点后两位)原式注意:计算过程中要多保留一位!
