新疆乌鲁木齐市米东区2024-2025学年八年级上学期期末检测数学试卷(含解析)
文档属性
| 名称 | 新疆乌鲁木齐市米东区2024-2025学年八年级上学期期末检测数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 20:17:05 | ||
图片预览



文档简介
新疆乌鲁木齐市米东区2024-2025学年八年级上学期期末检测数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.古城最美四月天,学科融合促发展.某校七年级开展项目式学习课程—在剪纸中感受轴对称的美.以下剪纸作品不是轴对称图形的是( )
A. B. C. D.
2.杭州亚运会主火炬以零碳甲醇作为燃料,在亚运史上首次实现废碳再生、循环内零碳排放.甲醇的密度很小,甲醇的质量约为0.00079,将0.00079用科学记数法表示应为( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.在下列长度的三条线段中,不能组成三角形的是( )
A. B.
C. D.
5.如图,在中,是高,是中线,若,,则的长为( ).
A.1 B. C.2 D.4
6.已知一个多边形的每个内角都是,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
7.如果把分式中的、同时扩大为原来的2倍,那么分式的值( )
A.缩小为原来的 B.扩大为原来的2倍
C.扩大为原来的4倍 D.不变
8.某学校学生进行急行军训练,预计行60千米的路程在下午5时到达,后来由于把速度加快20%,结果于下午4时到达,求原计划行军的速度.设原计划行军的速度为,则可列方程( )
A. B.
C. D.
9.如图,在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,,作直线,交于点,连接.若的周长为12,,则的周长为( )
A.10 B.9 C.8 D.7
10.如图,在中,,于点D,平分,且于点E,与相交于点F,H是边的中点,连接与相交于G,下列结论:①;②;③;④;⑤是等腰三角形.其中正确的有( )
A.5个 B.2个 C.4个 D.3个
二、填空题
11.建高楼通常用吊塔来吊建筑材料,而吊塔的上部是三角形结构,这是应用了三角形的 .
12.若使分式有意义,则x的取值范围是 .
13.已知点与关于轴对称,则 .
14.已知,,则的值是 .
15.定义,当,则的值为 .
16.如图,在四边形中,,E,F分别是上的点,当的周长最小时,的度数为 .
三、解答题
17.分解因式:
(1)
(2)
18.先化简,再求值:,其中,.
19.先化简:,再选择一个你认为合适的值代入求值.
20.如图,四边形中,对角线、交于点,,点是上一点,且,,求证:.
21.如图所示的正方形网格中,每个小正方形的边长都为1,,的顶点都在网格线的交点上,在图中建立平面直角坐标系,使与关于y轴对称,点C的坐标为.
(1)在图中画出平面直角坐标系;
(2)①写出点B关于x轴的对称点的坐标;
②画出关于x轴对称的图形,其中点A的对称点是,点C的对称点是.
22.人工智能在物流行业有广泛的应用,其中自主移动机器人可以实现高效的搬运和拣货作业.某物流园区利用,两种自主移动机器人搬运化工原料,型机器人比型机器人每小时多搬运,型机器人搬运所用时间与型机器人搬运所用时间相等,两种机器人每小时分别搬运多少化工原料?
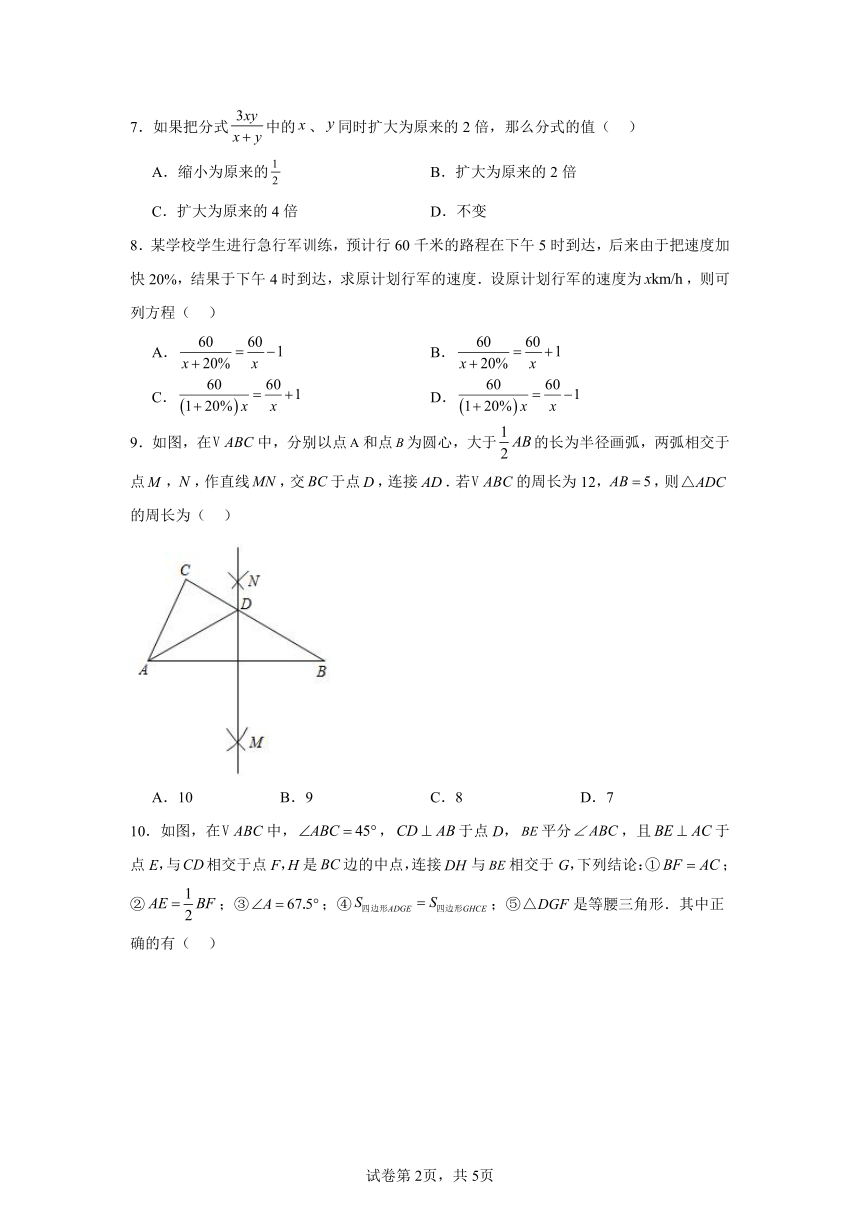
23.如图,某公园有一块长为,宽为的长方形空地,规划部门计划在其内部修建一个底座边长为的正方形雕像,左右两边修两条宽为am的长方形道路,其余部分(阴影)种植花卉.
(1)用含a,b,的式子表示种植花卉的面积;
(2)若,,请求出种植花卉的面积.
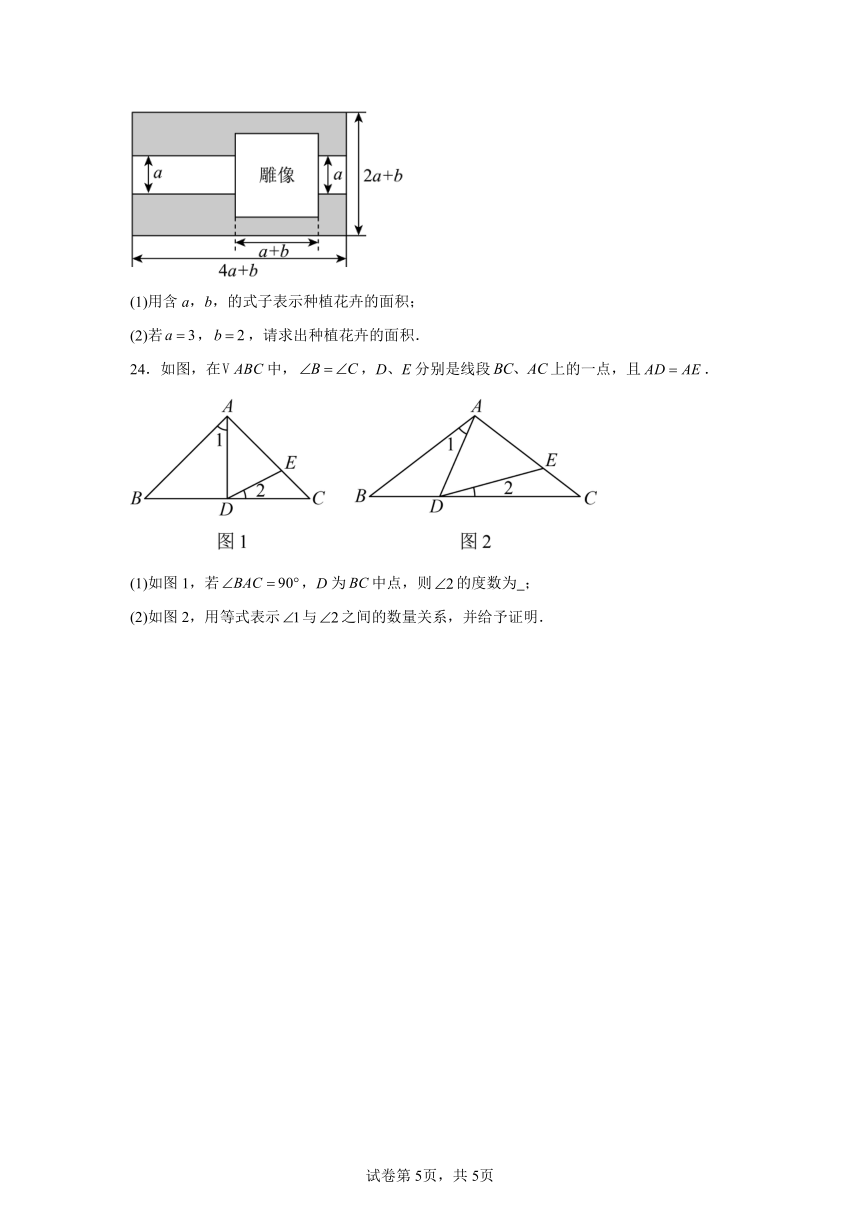
24.如图,在中,,D、E分别是线段上的一点,且.
(1)如图1,若,D为中点,则的度数为 ;
(2)如图2,用等式表示与之间的数量关系,并给予证明.
试卷第1页,共3页
试卷第1页,共3页
《新疆乌鲁木齐市米东区2024-2025学年八年级上学期期末检测数学试卷》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C C D D B D D C
1.B
【分析】本题考查了轴对称图形的定义;平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,就叫做轴对称图形;据此进行逐项分析,即可作答.
【详解】
解:A、 是轴对称图形,不符合题意,故该选项是错误的;
B、不是轴对称图形,符合题意,故该选项是正确的;
C、 是轴对称图形,不符合题意,故该选项是错误的;
D、 是轴对称图形,不符合题意,故该选项是错误的;
故选:B.
2.B
【分析】本题考查科学记数法,根据科学记数法的表示方法:为整数,进行表示即可.
【详解】解:;
故选B.
3.C
【分析】此题考查了幂的运算、合并同类项、平方差公式等知识,根据运算法则和乘法公式计算后即可得到答案.
【详解】解:A.,故选项错误,不符合题意;
B.,故选项错误,不符合题意;
C.,故选项正确,符合题意;
D.与不是同类项,不能合并,故选项错误,不符合题意.
故选:C.
4.C
【分析】本题考查了三角形的三边关系,熟练掌握三角形任意两边之和大于第三边是解题的关键.根据三角形任意两边之和大于第三边,对选项逐个分析即可.
【详解】解:,能组成三角形,故A选项错误;
,能组成三角形,故B选项错误;
,不能组成三角形,故C选项正确;
,能组成三角形,故D选项错误.
故选:C.
5.D
【分析】直接利用三角形面积公式求得,再根据中线的性质即可求解.
【详解】解:∵,,即,
∴
∵是中线,即点是的中点,
∴,
故选:D.
【点睛】本题考查三角形面积和中线的性质,解题的关键是熟练掌握三角形面积公式求得.
6.D
【分析】本题主要考查了多边形内角和外角综合,正多边形的一个内角度数与一个外角的度数之和为180度,据此可得这个多边形的每个外角的度数为,再根据外角和为即可求出边数.
【详解】解:∵一个多边形的每个内角都是,
∴这个多边形的每个外角的度数为,
∴这个多边形的边数为,
故选:D.
7.B
【分析】依题意,分别用和去代换原分式中的x和y,利用分式的基本性质化简即可.
【详解】解:把分式中的、同时扩大为原来的2倍得:,
∵,
∴把分式中的、同时扩大为原来的2倍,那么分式的值扩大为原来的2倍,
故选:B.
【点睛】本题主要考查了分式的基本性质,解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.
8.D
【分析】关键描述语是:“于下午4时到达”.等量关系为:原计划用的时间实际用的时间.
【详解】解:原计划用的时间,实际用的时间为,
则可列方程为:,即:.
故选:D.
【点睛】本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.本题的难点是得到实际用的时间,易错点是得到原计划用的时间与时间时间的差.
9.D
【分析】根据题意可知MN是AB的垂直平分线,可得AD=BD,再根据△ABC的周长和AB的长,求出AC+BC,即可得出△ADC的周长.
【详解】根据题意可知MN是AB的垂直平分线,
∴AD=BD.
∵△ABC的周长为12,
∴AB+BC+AC=12.
∵AB=5,
∴BC+AC=7,
即AC+CD+BD=7,
∴AC+CD+AD=7,
所以△ADC的周长为7.
故选:D.
【点睛】本题主要考查了尺规作线段垂直平分线,线段垂直平分线的性质,求三角形的周长等,将两边长的和转化为三角形的周长是解题的关键.
10.C
【分析】只要证明、,即可判断①②正确,根据角平分线的定义利用即可判断③;过G作于点M,根据角平分线定理,结合,可得,又可得,即可判断④错误,证明可判断⑤正确.
【详解】①,
,
,
又,
,
,
,
又,
,
∴是等腰直角三角形,
,
在和中,
,
,
.故①正确;
②平分,,
,,
在和中,
,
,
,
,
又,
,
即:,故②正确;
③,平分,
,
,
,
,故③正确;
④如图所示,过G作于点M,
为等腰直角斜边BC的中点,
,即,
又平分,,
,
又,
,
又
,
,,
,故④错误;
⑤,,,
,
又,
,
为等腰三角形,故⑤正确.
正确的为①②③⑤,共计4个,
故选:C.
【点睛】此题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,全等三角形的性质和判定,三角形的面积等知识点的综合运用,第四个问题难度比较大,添加辅助线是解题关键.
11.稳定性.
【分析】根据三角形具有稳定性解答.
【详解】解:吊塔的上部是三角形结构,这是利用了三角形的稳定性.
故答案为:稳定性.
【点睛】本题考查三角形的稳定性在实际生活中的应用,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
12.
【分析】由分母不为零可得,从而可得答案.
【详解】解:∵分式有意义,
∴,
解得:,
故答案为:.
【点睛】本题考查的是分式有意义的条件,掌握“分式的分母不为零”是解本题的关键.
13.
【分析】本题考查关于轴对称的点的坐标特征,解题的关键是掌握关于轴对称的点的坐标变化规律.
根据关于轴对称的点的坐标特征,求出a,b的值,再代入计算.
【详解】∵点与关于轴对称,
,
将代入,
,
故答案为.
14.
【分析】利用直接提取公因式进行分解因式,然后将已知代入即可得出答案.
【详解】解:∵,.
∴
.
故答案为:.
【点睛】本题主要考查了直接提取公因式法分解因式以及代数式求值,熟练掌握直接提取公因式法分解因式是解题关键.
15.2
【分析】本题考查新定义运算和解分式方程,解题的关键是根据新定义将等式转化为常规方程.
先根据新定义分别表示出和,再根据等式建立方程,最后求解方程得出的值.
【详解】,
.
解得:,
经检验,当时,,
是原方程的解,
故答案为:2.
16./度
【分析】本题考查了轴对称—最短路径问题,四边形内角和定理,三角形外角的性质.首先作点关于,的对称点,,延长到点,根据轴对称的性质可得,,,,由“两点之间线段最短”可知当,,,四点共线时,的周长最小,由四边形内角和为可得,再由三角形的外角等于不相邻的两个内角之和,进行角的和差计算,即可得到答案.
【详解】解:如图,作点关于,的对称点,,延长到点,
∴,,
∴,,
的周长,
当,,,四点共线时,的周长最小,
,,
,
,
,
,,
.
故答案为:.
17.(1)
(2)
【分析】本题考查因式分解,解题的关键是熟练运用提取公因式法和公式法进行因式分解.
(1)先提取公因式,再利用完全平方公式;
(2)把看成一个整体,利用完全平方公式进行因式分解.
【详解】(1)解:
;
(2)解:
.
18.;1
【分析】本题考查整式的化简求值,涉及多项式除以单项式以及平方差公式,解题的关键是正确运用运算法则对整式进行化简.
先根据多项式除以单项式的法则计算,再根据平方差公式计算,然后去括号,合并同类项进行化简,最后将x,y的值代入化简后的式子求值.
【详解】解:
,
当时,代入上式可得:
原式=
.
19.;当时,原式.
【分析】本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则进行化简,并注意代入的值要使原分式有意义.
先对括号内的式子进行通分计算,再将除法运算转化为乘法运算,然后对分子分母进行因式分解,最后约分得到最简形式,再选取合适的值代入求值.
【详解】解:
,
当,原式.
20.见解析
【分析】本题考查全等三角形的判定与性质,解题的关键是通过角的等量关系找到证明三角形全等的条件.
根据已知条件可得,结合,,可证明,从而得到.
【详解】证明:,
,
.
在和中,
,
,
.
21.(1)见解析
(2)①;②见解析
【分析】(1)先根据“与关于y轴对称”建立y轴,再根据C的坐标为建立x轴;
(2)①直接根据关于x轴对称的点的坐标规律作答即可;②先找到,的位置,再画图即可.
【详解】(1)解:平面直角坐标系如下图所示;
(2)解:①由(1)中建的平面直角坐标系可知点B的坐标为,
因此点B关于x轴的对称点的坐标为;
②如图所示.
【点睛】本题考查了轴对称的性质、关于x轴对称的点的坐标规律、作轴对称图形,正确画出坐标轴是解题的关键.
22.A种机器人每小时搬运化工原料,B种机器人每小时搬运化工原料.
【分析】设B种机器人每小时搬运化工原料,则A种机器人每小时搬运化工原料,由题意:A型机器人搬运所用时间与B型机器人搬运所用时间相等,列出分式方程,解方程即可.
【详解】解:设B种机器人每小时搬运化工原料,则A种机器人每小时搬运化工原料,
根据题意得:,
解得:,
经检验,为原方程的解,且符合题意,
则,
答:A种机器人每小时搬运化工原料,B种机器人每小时搬运化工原料.
【点睛】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解此题的关键.
23.(1)
(2)
【分析】此题考查了多项式的乘法与图形面积,完全平方公式的应用,熟练的利用图形面积差列出正确的代数式是解本题的关键.
(1)根据图形的面积之差列式:,再计算即可;
(2)把,代入(1)中化简后的代数式计算即可.
【详解】(1)解:种植花卉=,
,
;
(2)当,,
原式.
24.(1)
(2).证明见解析
【分析】本题主要考查了等腰三角形的性质,三角形外角的性质,熟知三角形一个外角的度数等于与其不相邻的两个内角之和是解题的关键.
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,,,再根据等边对等角的性质,,进而得出.进而得出.
(2)根据三角形的一个外角等于和它不相邻的两个内角的和,,,再根据等边对等角的性质,,进而得出.
【详解】(1)解:∵,
∴,
∵,D是中点,
∴,
∵,
∴,即,
∴;
故答案为:.
(2)解:,证明如下:
∵,
∴,
∵,,
∴,
∴,
即.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.古城最美四月天,学科融合促发展.某校七年级开展项目式学习课程—在剪纸中感受轴对称的美.以下剪纸作品不是轴对称图形的是( )
A. B. C. D.
2.杭州亚运会主火炬以零碳甲醇作为燃料,在亚运史上首次实现废碳再生、循环内零碳排放.甲醇的密度很小,甲醇的质量约为0.00079,将0.00079用科学记数法表示应为( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.在下列长度的三条线段中,不能组成三角形的是( )
A. B.
C. D.
5.如图,在中,是高,是中线,若,,则的长为( ).
A.1 B. C.2 D.4
6.已知一个多边形的每个内角都是,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
7.如果把分式中的、同时扩大为原来的2倍,那么分式的值( )
A.缩小为原来的 B.扩大为原来的2倍
C.扩大为原来的4倍 D.不变
8.某学校学生进行急行军训练,预计行60千米的路程在下午5时到达,后来由于把速度加快20%,结果于下午4时到达,求原计划行军的速度.设原计划行军的速度为,则可列方程( )
A. B.
C. D.
9.如图,在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,,作直线,交于点,连接.若的周长为12,,则的周长为( )
A.10 B.9 C.8 D.7
10.如图,在中,,于点D,平分,且于点E,与相交于点F,H是边的中点,连接与相交于G,下列结论:①;②;③;④;⑤是等腰三角形.其中正确的有( )
A.5个 B.2个 C.4个 D.3个
二、填空题
11.建高楼通常用吊塔来吊建筑材料,而吊塔的上部是三角形结构,这是应用了三角形的 .
12.若使分式有意义,则x的取值范围是 .
13.已知点与关于轴对称,则 .
14.已知,,则的值是 .
15.定义,当,则的值为 .
16.如图,在四边形中,,E,F分别是上的点,当的周长最小时,的度数为 .
三、解答题
17.分解因式:
(1)
(2)
18.先化简,再求值:,其中,.
19.先化简:,再选择一个你认为合适的值代入求值.
20.如图,四边形中,对角线、交于点,,点是上一点,且,,求证:.
21.如图所示的正方形网格中,每个小正方形的边长都为1,,的顶点都在网格线的交点上,在图中建立平面直角坐标系,使与关于y轴对称,点C的坐标为.
(1)在图中画出平面直角坐标系;
(2)①写出点B关于x轴的对称点的坐标;
②画出关于x轴对称的图形,其中点A的对称点是,点C的对称点是.
22.人工智能在物流行业有广泛的应用,其中自主移动机器人可以实现高效的搬运和拣货作业.某物流园区利用,两种自主移动机器人搬运化工原料,型机器人比型机器人每小时多搬运,型机器人搬运所用时间与型机器人搬运所用时间相等,两种机器人每小时分别搬运多少化工原料?
23.如图,某公园有一块长为,宽为的长方形空地,规划部门计划在其内部修建一个底座边长为的正方形雕像,左右两边修两条宽为am的长方形道路,其余部分(阴影)种植花卉.
(1)用含a,b,的式子表示种植花卉的面积;
(2)若,,请求出种植花卉的面积.
24.如图,在中,,D、E分别是线段上的一点,且.
(1)如图1,若,D为中点,则的度数为 ;
(2)如图2,用等式表示与之间的数量关系,并给予证明.
试卷第1页,共3页
试卷第1页,共3页
《新疆乌鲁木齐市米东区2024-2025学年八年级上学期期末检测数学试卷》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C C D D B D D C
1.B
【分析】本题考查了轴对称图形的定义;平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,就叫做轴对称图形;据此进行逐项分析,即可作答.
【详解】
解:A、 是轴对称图形,不符合题意,故该选项是错误的;
B、不是轴对称图形,符合题意,故该选项是正确的;
C、 是轴对称图形,不符合题意,故该选项是错误的;
D、 是轴对称图形,不符合题意,故该选项是错误的;
故选:B.
2.B
【分析】本题考查科学记数法,根据科学记数法的表示方法:为整数,进行表示即可.
【详解】解:;
故选B.
3.C
【分析】此题考查了幂的运算、合并同类项、平方差公式等知识,根据运算法则和乘法公式计算后即可得到答案.
【详解】解:A.,故选项错误,不符合题意;
B.,故选项错误,不符合题意;
C.,故选项正确,符合题意;
D.与不是同类项,不能合并,故选项错误,不符合题意.
故选:C.
4.C
【分析】本题考查了三角形的三边关系,熟练掌握三角形任意两边之和大于第三边是解题的关键.根据三角形任意两边之和大于第三边,对选项逐个分析即可.
【详解】解:,能组成三角形,故A选项错误;
,能组成三角形,故B选项错误;
,不能组成三角形,故C选项正确;
,能组成三角形,故D选项错误.
故选:C.
5.D
【分析】直接利用三角形面积公式求得,再根据中线的性质即可求解.
【详解】解:∵,,即,
∴
∵是中线,即点是的中点,
∴,
故选:D.
【点睛】本题考查三角形面积和中线的性质,解题的关键是熟练掌握三角形面积公式求得.
6.D
【分析】本题主要考查了多边形内角和外角综合,正多边形的一个内角度数与一个外角的度数之和为180度,据此可得这个多边形的每个外角的度数为,再根据外角和为即可求出边数.
【详解】解:∵一个多边形的每个内角都是,
∴这个多边形的每个外角的度数为,
∴这个多边形的边数为,
故选:D.
7.B
【分析】依题意,分别用和去代换原分式中的x和y,利用分式的基本性质化简即可.
【详解】解:把分式中的、同时扩大为原来的2倍得:,
∵,
∴把分式中的、同时扩大为原来的2倍,那么分式的值扩大为原来的2倍,
故选:B.
【点睛】本题主要考查了分式的基本性质,解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.
8.D
【分析】关键描述语是:“于下午4时到达”.等量关系为:原计划用的时间实际用的时间.
【详解】解:原计划用的时间,实际用的时间为,
则可列方程为:,即:.
故选:D.
【点睛】本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.本题的难点是得到实际用的时间,易错点是得到原计划用的时间与时间时间的差.
9.D
【分析】根据题意可知MN是AB的垂直平分线,可得AD=BD,再根据△ABC的周长和AB的长,求出AC+BC,即可得出△ADC的周长.
【详解】根据题意可知MN是AB的垂直平分线,
∴AD=BD.
∵△ABC的周长为12,
∴AB+BC+AC=12.
∵AB=5,
∴BC+AC=7,
即AC+CD+BD=7,
∴AC+CD+AD=7,
所以△ADC的周长为7.
故选:D.
【点睛】本题主要考查了尺规作线段垂直平分线,线段垂直平分线的性质,求三角形的周长等,将两边长的和转化为三角形的周长是解题的关键.
10.C
【分析】只要证明、,即可判断①②正确,根据角平分线的定义利用即可判断③;过G作于点M,根据角平分线定理,结合,可得,又可得,即可判断④错误,证明可判断⑤正确.
【详解】①,
,
,
又,
,
,
,
又,
,
∴是等腰直角三角形,
,
在和中,
,
,
.故①正确;
②平分,,
,,
在和中,
,
,
,
,
又,
,
即:,故②正确;
③,平分,
,
,
,
,故③正确;
④如图所示,过G作于点M,
为等腰直角斜边BC的中点,
,即,
又平分,,
,
又,
,
又
,
,,
,故④错误;
⑤,,,
,
又,
,
为等腰三角形,故⑤正确.
正确的为①②③⑤,共计4个,
故选:C.
【点睛】此题是三角形综合题,考查了等腰三角形的性质,直角三角形的性质,全等三角形的性质和判定,三角形的面积等知识点的综合运用,第四个问题难度比较大,添加辅助线是解题关键.
11.稳定性.
【分析】根据三角形具有稳定性解答.
【详解】解:吊塔的上部是三角形结构,这是利用了三角形的稳定性.
故答案为:稳定性.
【点睛】本题考查三角形的稳定性在实际生活中的应用,当三角形三边的长度确定后,三角形的形状和大小就能唯一确定下来,故三角形具有稳定性.
12.
【分析】由分母不为零可得,从而可得答案.
【详解】解:∵分式有意义,
∴,
解得:,
故答案为:.
【点睛】本题考查的是分式有意义的条件,掌握“分式的分母不为零”是解本题的关键.
13.
【分析】本题考查关于轴对称的点的坐标特征,解题的关键是掌握关于轴对称的点的坐标变化规律.
根据关于轴对称的点的坐标特征,求出a,b的值,再代入计算.
【详解】∵点与关于轴对称,
,
将代入,
,
故答案为.
14.
【分析】利用直接提取公因式进行分解因式,然后将已知代入即可得出答案.
【详解】解:∵,.
∴
.
故答案为:.
【点睛】本题主要考查了直接提取公因式法分解因式以及代数式求值,熟练掌握直接提取公因式法分解因式是解题关键.
15.2
【分析】本题考查新定义运算和解分式方程,解题的关键是根据新定义将等式转化为常规方程.
先根据新定义分别表示出和,再根据等式建立方程,最后求解方程得出的值.
【详解】,
.
解得:,
经检验,当时,,
是原方程的解,
故答案为:2.
16./度
【分析】本题考查了轴对称—最短路径问题,四边形内角和定理,三角形外角的性质.首先作点关于,的对称点,,延长到点,根据轴对称的性质可得,,,,由“两点之间线段最短”可知当,,,四点共线时,的周长最小,由四边形内角和为可得,再由三角形的外角等于不相邻的两个内角之和,进行角的和差计算,即可得到答案.
【详解】解:如图,作点关于,的对称点,,延长到点,
∴,,
∴,,
的周长,
当,,,四点共线时,的周长最小,
,,
,
,
,
,,
.
故答案为:.
17.(1)
(2)
【分析】本题考查因式分解,解题的关键是熟练运用提取公因式法和公式法进行因式分解.
(1)先提取公因式,再利用完全平方公式;
(2)把看成一个整体,利用完全平方公式进行因式分解.
【详解】(1)解:
;
(2)解:
.
18.;1
【分析】本题考查整式的化简求值,涉及多项式除以单项式以及平方差公式,解题的关键是正确运用运算法则对整式进行化简.
先根据多项式除以单项式的法则计算,再根据平方差公式计算,然后去括号,合并同类项进行化简,最后将x,y的值代入化简后的式子求值.
【详解】解:
,
当时,代入上式可得:
原式=
.
19.;当时,原式.
【分析】本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则进行化简,并注意代入的值要使原分式有意义.
先对括号内的式子进行通分计算,再将除法运算转化为乘法运算,然后对分子分母进行因式分解,最后约分得到最简形式,再选取合适的值代入求值.
【详解】解:
,
当,原式.
20.见解析
【分析】本题考查全等三角形的判定与性质,解题的关键是通过角的等量关系找到证明三角形全等的条件.
根据已知条件可得,结合,,可证明,从而得到.
【详解】证明:,
,
.
在和中,
,
,
.
21.(1)见解析
(2)①;②见解析
【分析】(1)先根据“与关于y轴对称”建立y轴,再根据C的坐标为建立x轴;
(2)①直接根据关于x轴对称的点的坐标规律作答即可;②先找到,的位置,再画图即可.
【详解】(1)解:平面直角坐标系如下图所示;
(2)解:①由(1)中建的平面直角坐标系可知点B的坐标为,
因此点B关于x轴的对称点的坐标为;
②如图所示.
【点睛】本题考查了轴对称的性质、关于x轴对称的点的坐标规律、作轴对称图形,正确画出坐标轴是解题的关键.
22.A种机器人每小时搬运化工原料,B种机器人每小时搬运化工原料.
【分析】设B种机器人每小时搬运化工原料,则A种机器人每小时搬运化工原料,由题意:A型机器人搬运所用时间与B型机器人搬运所用时间相等,列出分式方程,解方程即可.
【详解】解:设B种机器人每小时搬运化工原料,则A种机器人每小时搬运化工原料,
根据题意得:,
解得:,
经检验,为原方程的解,且符合题意,
则,
答:A种机器人每小时搬运化工原料,B种机器人每小时搬运化工原料.
【点睛】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解此题的关键.
23.(1)
(2)
【分析】此题考查了多项式的乘法与图形面积,完全平方公式的应用,熟练的利用图形面积差列出正确的代数式是解本题的关键.
(1)根据图形的面积之差列式:,再计算即可;
(2)把,代入(1)中化简后的代数式计算即可.
【详解】(1)解:种植花卉=,
,
;
(2)当,,
原式.
24.(1)
(2).证明见解析
【分析】本题主要考查了等腰三角形的性质,三角形外角的性质,熟知三角形一个外角的度数等于与其不相邻的两个内角之和是解题的关键.
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,,,再根据等边对等角的性质,,进而得出.进而得出.
(2)根据三角形的一个外角等于和它不相邻的两个内角的和,,,再根据等边对等角的性质,,进而得出.
【详解】(1)解:∵,
∴,
∵,D是中点,
∴,
∵,
∴,即,
∴;
故答案为:.
(2)解:,证明如下:
∵,
∴,
∵,,
∴,
∴,
即.
答案第1页,共2页
答案第1页,共2页
同课章节目录
