2.5角的度量(一)暑假预习练(含解析) 北师大版数学四年级上册
文档属性
| 名称 | 2.5角的度量(一)暑假预习练(含解析) 北师大版数学四年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 617.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 06:24:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.5角的度量(一)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.图中所有锐角的和是90°,那么∠AOB是( )。
A.15° B.30° C.45°
2.任意两个锐角的度数之和,与直角的度数相比,( )。
A.等于直角的度数 B.比直角的度数大
C.比直角的度数小 D.不确定
3.从3时到8时,时针旋转了( )。
A.120° B.150° C.170°
4.估一估,如图中台灯灯秆夹角大约是( )。
A.60° B.90° C.120° D.160°
5.下面说法正确的是( )。
A.射线是直线的一部分,所以射线比直线短。
B.把一个30度的角放在10倍放大镜下观察,角变成300°。
C.一个九位数,它的最高位的计数单位是亿位。
D.在6和7之间添上7个0,这个数才能成为六亿零七。
6.放风筝比赛时,规定用30米长的线,如果把每根风筝线的一端固定在地面上,风筝线和地面所形成的角如图,风筝( )放得最高。
A.① B.② C.③ D.不确定
7.把一个50°的角两边分别延长,得到的角的度数是( )。
A.100° B.50° C.不能确定
8.比一比,( )角大。
A.左边的 B.右边 C.一样 D.无法比较
9.20°的角中包含( )个1°的角。
A.20 B.10 C.45 D.2
10.下列情况中,角会变大的是( )。
A.用放大镜看角 B.把角的两边画得更长 C.让角的开口张大一些
二、填空题
11.分一分。
1° 15° 134° 78° 110° 23° 89°
锐角: ;
钝角: 。
12.钟面上,( )时整,时针与分针所成的角是平角,( )时整,时针与分针所成的角是周角。
13.钟表上的时间为10:50时,时针与分针形成的较小夹角是( )度。
14.一个角比直角大25°,它的度数是( ),它是( )角;一个角比直角小32°,它的度数是( ),它是( )角。
15.把一个半圆平均分成4份,每一份是( )度。
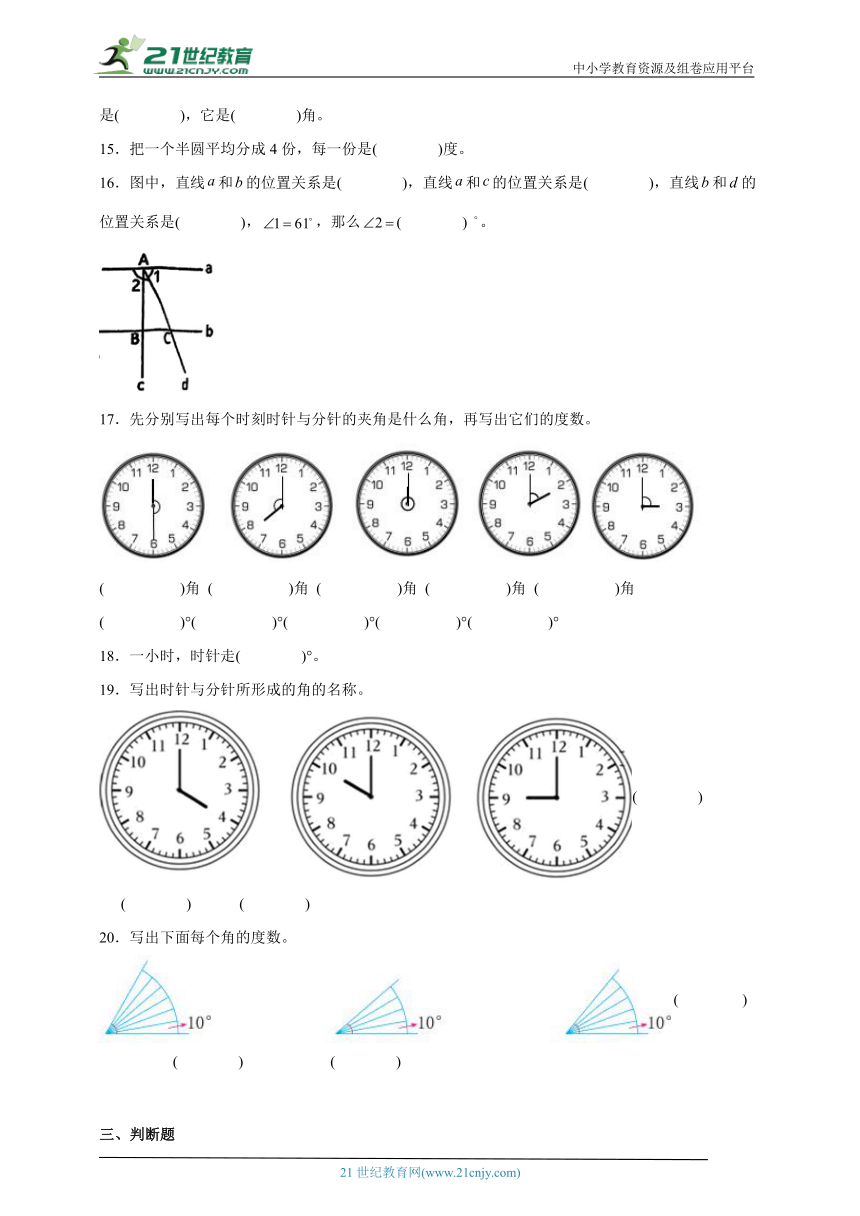
16.图中,直线和的位置关系是( ),直线和的位置关系是( ),直线和的位置关系是( ),,那么( )。
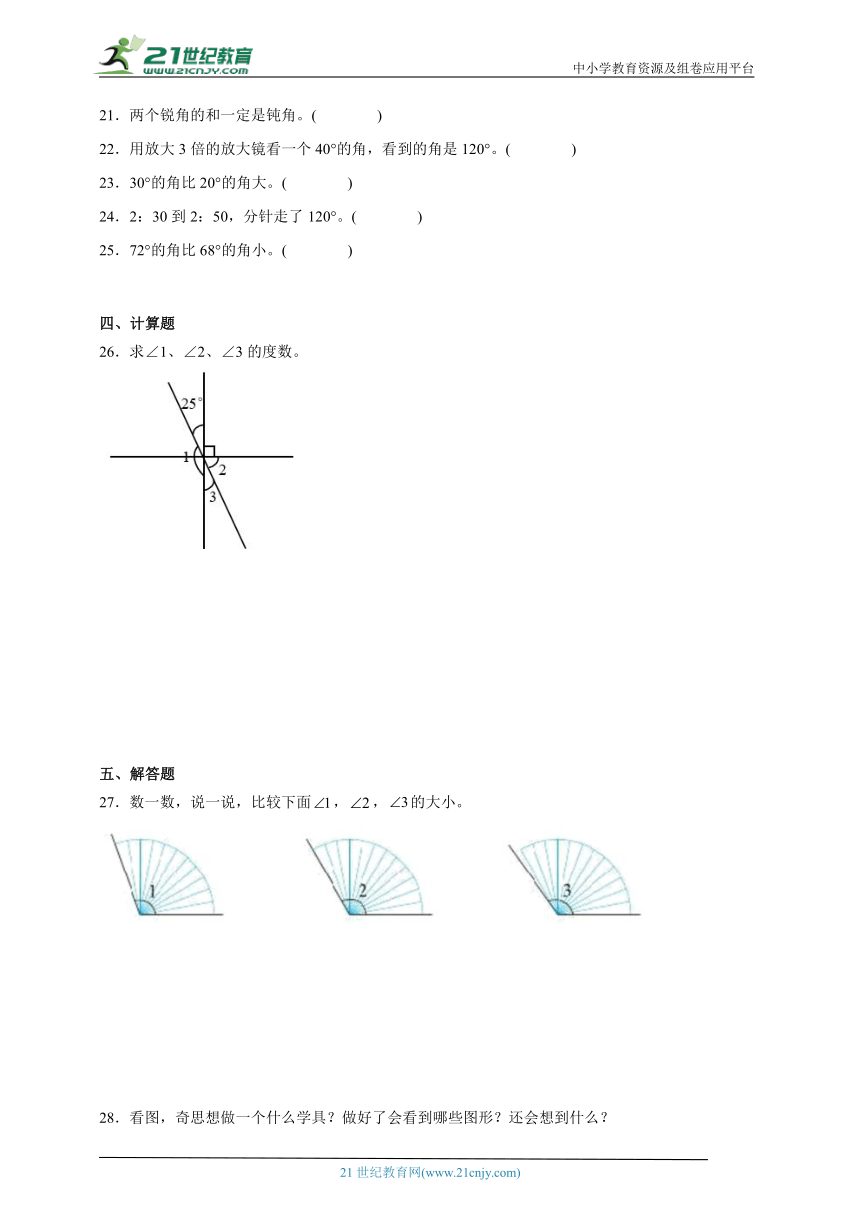
17.先分别写出每个时刻时针与分针的夹角是什么角,再写出它们的度数。
( )角 ( )角 ( )角 ( )角 ( )角
( )°( )°( )°( )°( )°
18.一小时,时针走( )°。
19.写出时针与分针所形成的角的名称。
( ) ( ) ( )
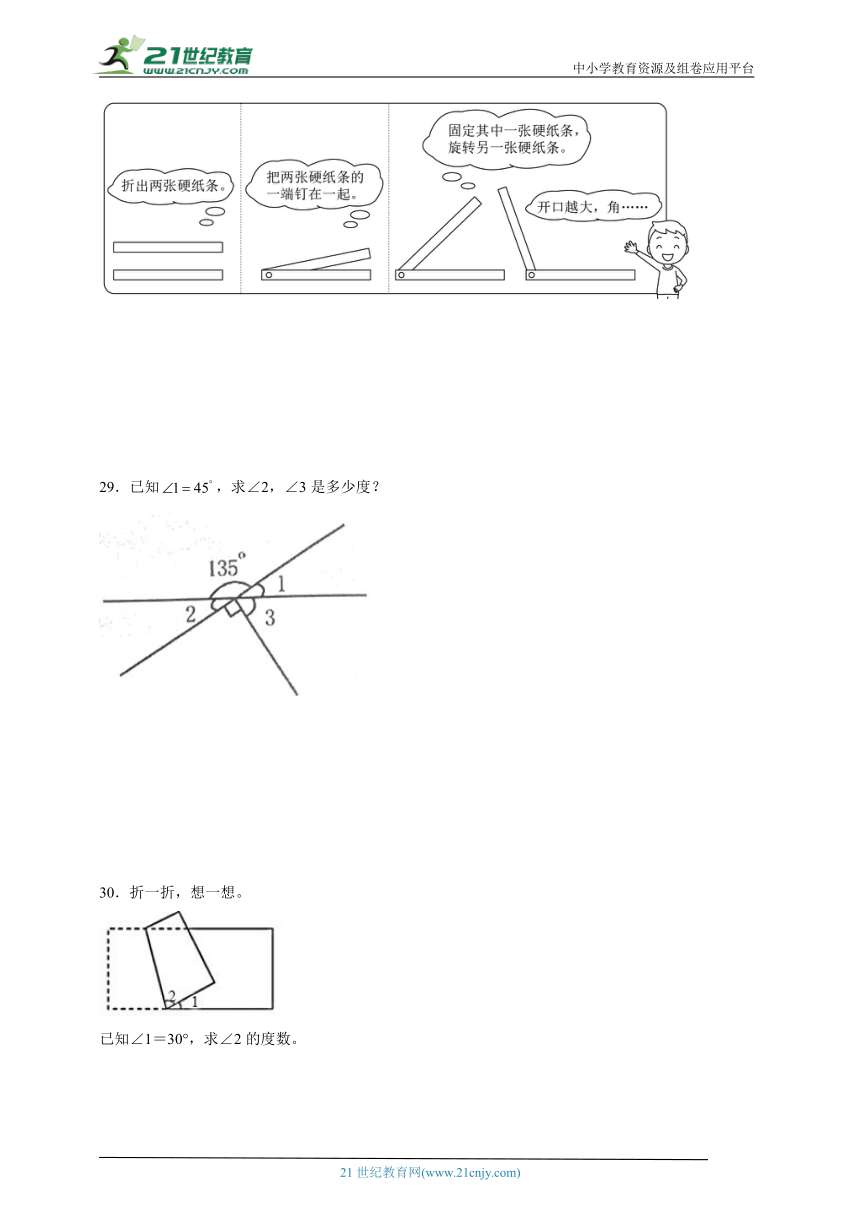
20.写出下面每个角的度数。
( ) ( ) ( )
三、判断题
21.两个锐角的和一定是钝角。( )
22.用放大3倍的放大镜看一个40°的角,看到的角是120°。( )
23.30°的角比20°的角大。( )
24.2:30到2:50,分针走了120°。( )
25.72°的角比68°的角小。( )
四、计算题
26.求∠1、∠2、∠3的度数。
五、解答题
27.数一数,说一说,比较下面,,的大小。
28.看图,奇思想做一个什么学具?做好了会看到哪些图形?还会想到什么?
29.已知,求∠2,∠3是多少度?
30.折一折,想一想。
已知∠1=30°,求∠2的度数。
31.下面是一把打开后的折扇,每相邻两条折痕的夹角的度数都是9°,不算两边,一共有12条折痕,这把折扇左右两个木条的夹角度数是多少?(木条与折痕的夹角也是9°)
《2.5角的度量(一)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C D A B C A C
1.C
【分析】解决本题时应先明确图中的锐角分别是哪几个角,进而明确这些锐角之间的关系,再进一步解答即可。如图所示,图中的锐角共3个,即∠AOC、∠COB和∠AOB。∠AOC+∠COB+∠AOB=90°,而∠AOC+∠COB=∠AOB,则∠AOB=90°÷2。
【详解】
∠AOB=90°÷2=45°
故答案为:C
2.D
【分析】锐角是指大于0°且小于90°的角,两个锐角之和有可能大于90°,也有可能小于90°,也有可能等于90°。
【详解】假如两个锐角是30°和40°,和就是70°,比直角度数小;假如两个锐角是70°和30°,和就是100°,比直角度数大;假如两个锐角分别都是45°,那么相加之和就等于直角度数。所以答案不确定。
故答案为:D
3.B
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°。从3时到8时,时针走了5个大格,旋转了5×30°。
【详解】5×30°=150°,从3时到8时,时针旋转了150°。
故答案为:B
【点睛】明确钟面上每个大格是30°,这是解决本题的关键。
4.C
【分析】观察图形可知,台灯灯杆夹角是一个钝角,所以,排除A、B,但是这个角的大小更接近直角,所以排除D,选择C即可。
【详解】根据分析可知,图中台灯灯杆夹角大约是120°。
故答案为:C
5.D
【分析】直线没有端点,可以向两端无限延伸,不能度量长度;射线有一个端点,可以向一端无限延伸,不能度量长度;
角的大小与两条边的长短无关,只与角两条边张开的大小有关;
从右边起,亿位在第九位,它的计数单位是“亿”;
读亿以上的数时,先读亿级,再读万级,最后读个级,亿级、万级的数要按照个级的数的读法来读,再在末尾加上“亿”、“万”,每级末尾不管有几个0,都不读,其余数位有一个0或连续几个0,都只读一个。据此解答。
【详解】A.由分析可知,直线和射线都不能度量长度,所以无法比较它们的长度关系,选项错误;
B.把角放在放大镜下观看,放大的角两边的长度,角两边张开大小不变,角的大小不变,选项错误;
C.由分析可知,九位数的最高位是亿位,计数单位是“亿”,选项错误;
D.6和7之间添上7个0,这个数变成600000007,读作六亿零七,选项正确。
故答案为:D
6.A
【分析】因为线的长度是固定的都是30米,所以谁与地面的夹角接近90度,谁的高度就高;观察上图可知,三条线中,①与地面的夹角最接近90度,所以①放的最高,据此解答。
【详解】根据分析得:①与地面的夹角最接近90度,所以①放的最高。
故答案为:A
7.B
【分析】把一个角两边分别延长,但没有改变角两边叉开的大小,则角的度数不变。
【详解】把一个50°的角两边分别延长,得到的角的度数是50°。
故答案为:B
【点睛】角的大小跟两边叉开的大小有关,跟边的长短无关。
8.C
【分析】观察上图可知,两个角都是直角,一样大,据此即可解答。
【详解】根据分析可知,两个角一样大。
故答案为:C
【点睛】本题主要考查学生对角的分类知识的掌握和灵活运用。
9.A
【分析】根据求一个数里面有几个另一个数,用除法列式计算即可。
【详解】20°÷1°=20(个),则20°的角中包含20个1°的角。
胡答案为:A
【点睛】一个角度数是几度,就包含几个1°的角。
10.C
【分析】角的大小取决于组成角的两条边张开的程度,张开的越大,角就越大,张开的越小,角就越小,与边的长短无关,放大镜不能改变角的两边张开的大小,因此不能改变角的度数,据此解答即可。
【详解】由题意经过分析,用放大镜看角和把角的两边画得更长,都不能改变角的大小,让角的开口张大一些可以使角变大。
故答案为:C
11. 1°、15°、78°、 23°、 89° 134°、110°
【分析】大于0°小于90°的角叫做锐角,大于90°小于180°的角叫做钝角,据此解答。
【详解】锐角:1°、15°、78°、 23°、 89°
钝角:134°、110°
【点睛】熟练掌握锐角和钝角的定义是解决本题的关键。
12. 6 12
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°。整时,分针指向12,要使时针和分针成平角,即180°,则分针指向6。要使分针与时针成周角,即360°,时针应指向12。
【详解】6×30°=180°,12×30°=360°
钟面上,6时整,时针与分针所成的角是平角,12时整,时针与分针所成的角是周角。
【点睛】本题考查钟面问题,明确钟面上每个大格是30°,这是解决本题的关键。
13.25
【分析】钟面上每相邻两个数字间的夹角是:360°÷12=30°,50分钟是1小时的,10:50时,分针指在10的位置,而时针走了两个数字之间(10和11之间)的,此时时针和分针的夹角是(30÷6×5)°。据此解答。
【详解】360°÷12=30°
50分钟是1小时的;
30°÷6×5
=5°×5
=25°
【点睛】本题考查的是求时针与分针夹角的问题,关键是明确时针走到10和11之间的什么位置。
14. 115° 钝 58° 锐
【分析】直角的度数为90°,一个角比直角大25°,它的度数用加法计算即可;一个角比直角小32°,它的度数用减法计算即可;大于90°,小于180°的角为钝角;大于0°,小于90°的角为锐角。
【详解】由于90°+25°=115°,180°>115°>90°;
90°-32°=58°,0°<58°<90°;
所以一个角比直角大25°,它的度数是115°,它是钝角;一个角比直角小32°,它的度数是58°,它是锐角。
【点睛】本题主要考查了角的分类及大小关系。
15.45
【分析】半圆也就是180度,把半圆平均分成4份,180度除以4等于一份的度数,据此即可解答。
【详解】180°÷4=45°
把一个半圆平均分成4份,每一份是45度。
【点睛】熟练掌握角的度数的表示方法是解答本题的关键。
16. 平行/互相平行 垂直/互相垂直 相交 119
【分析】在同一平面内,不相交的两条直线互相平行,其中一条直线是另一条直线的平行线;两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。据此判断几条直线的位置关系。由图可知,∠1和∠2组成了一个平角。∠1=61°,那么直接用180°减去61°即可算出∠2的度数。
【详解】由图可知,直线a和b没有交点,所以这两条直线互相平行。直线a和c相交成直角,所以这两条直线互相垂直。直线b和d有交点,所以这两条直线相交。
∠2=180°-∠1=180°-61°=119°
直线和的位置关系是平行,直线和的位置关系是垂直,直线和的位置关系是相交,,那么119°。
17. 平 钝 周 锐 直 180 120 360 60 90
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°。钟面上6时整,时针和分针之间有6个大格,则时针和分针的夹角是6×30°。钟面上8时整,时针和分针之间有4个大格,则时针和分针的夹角是4×30°。钟面上12时整,时针和分针之间有12个大格,则时针和分针的夹角是12×30°。钟面上2时整,时针和分针之间有2个大格,则时针和分针的夹角是2×30°。钟面上3时整,时针和分针之间有3个大格,则时针和分针的夹角是3×30°。再明确各个角的类型。
【详解】6×30°=180°
4×30°=120°
12×30°=360°
2×30°=60°
3×30°=90°
【点睛】本题考查角的度量和角的分类,明确钟面上每个大格是30°,这是解决本题的关键。
18.30
【分析】钟面上有12大格,每一大格对应的角是30度,一小时,时针走一大格,即走30°据此即可解答。
【详解】根据分析可知,一小时,时针走30°。
【点睛】熟练掌握钟面的相关知识是解答本题的关键。
19. 钝角 锐角 直角
【分析】钟面上有12个大格,每两个大格之间的夹角是30°,4时整时,时针和分针之间有4个大格,利用4×30°=120°,这是一个钝角;10时整时,时针和分针之间有2个大格,就用2×30°=60°,这是一个锐角;9时整时,时针和分针之间有3个大格,就用3×30°=90°,这是一个直角。
【详解】根据分析可知:
【点睛】本题考查了钟面角的认识,关键明白钟面上有12个大格,两个大格之间的夹角是30°。
20.
【分析】已知每个测量单位的度数是,分别数一数每个图中的大角中有几个单位,用测量单位的数量乘,据此可求出每个角的度数。
【详解】
第一个角是,第二个角是,第三角是。
21.×
【分析】小于90°的角叫做锐角,两个锐角的和小于180°,可能是锐角、直角或者钝角,据此判断。
【详解】例如10°+20°=30°,40°+50°=90°,60°+70°=130°,两个锐角的和可能是锐角、直角或者钝角,说法错误。
故答案为:×
【点睛】本题关键是熟记锐角、直角和钝角的定义,采用举反例的方法解答。
22.×
【分析】角的大小与角两边的长短无关,只与角开叉的大小有关,开叉越大,角就越大,据此即可解答。
【详解】用放大3倍的放大镜看一个40°的角,看到的角比原角的两边要长,但角的开叉大小没变,所以看到的角还是40°,原说法错误。
故答案为:×
【点睛】本题主要考查学生对影响角的大小因素的掌握和灵活运用。
23.√
【分析】比较两个角度数的大小,直接比较单位“°”前面数字的大小即可。
【详解】30°>20°,则30°的角比20°的角大。题干说法正确。
故答案为:√
【点睛】本题考查角的大小比较,需熟练掌握。
24.√
【分析】根据经过时间=结束时间-开始时间,可知从2:30到2:50,经过了20分钟。时钟上12个数字把钟面平均分成12个大格,每个大格是30°。经过20分钟则分针走4个大格,共走了4×30°。
【详解】2时50分-2时30分=20(分钟)
4×5=20(分钟)
4×30°=120°
则2:30到2:50,分针走了120°。
故答案为:√
【点睛】本题考查钟表问题,明确钟面上每个大格是30°,是解决本题的关键。
25.×
【分析】根据角的度数比较角的大小,度数越大的角就越大。
【详解】72°>68°,所以72°的角比68°的角小。
故答案为:×
【点睛】本题考查的是角的大小比较。
26.∠1=155°;∠2=65°;∠3=25°
【分析】观察可知,∠1与25°组成了一个平角(180°),那么∠1=180°-25°;∠1与∠3组成了一个平角,那么∠3=180°-∠1;∠2与∠3组成了一个直角(90°),那么∠2=90°-∠3。据此解答。
【详解】∠1=180°-25°=155°
∠3=180°-∠1=180°-155°=25°
∠2=90°-∠3=90°-25°=65°
27.∠3>∠2>∠1
【分析】结合所给图形,首先数出每个角中小刻度的个数,再根据角的大小与叉开的角度有关。结合每个角中小刻度的个数即可得出其答案。
【详解】∠1张开的角度是11个小刻度,∠2张开的角度是12个小刻度,∠3张开的角度是13个小刻度。因为每个刻度都相等,13>12>11,所以∠3>∠2>∠1。
28.见详解
【分析】从一点引出两条射线所形成的图形叫做角。这一点是角的顶点,两条射线是角的边。小于90°的角是锐角,90°的角叫做直角,大于90°小于180°的角叫做钝角,180°的角叫做平角,360°的角叫做周角,据此解答。
【详解】根据题目给出的信息可知,奇思想做一个关于角的学具,做好后会看到锐角、直角、钝角、平角和周角。能想到:角的大小跟两边叉开的大小有关,跟边的长短无关。
29.∠2=45°;∠3=45°
【分析】∠1与∠3组成了一个直角,那么∠3=90°-∠1;∠2与135°组成了一个平角,那么∠2=180°-135°。
【详解】∠3=90°-45°=45°
∠2=180°-135°=45°
【点睛】解答本题的关键是掌握直角等于90°,平角等于180°。
30.75°
【分析】
如图所示,将长方形纸折一折,得到的∠2=∠3,∠1、∠2和∠3组成一个平角,则∠2=(180°-∠1)÷2。
【详解】∠2=(180°-∠1)÷2=(180°-30°)÷2=150°÷2=75°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
31.117°
【分析】每相邻两条折痕形成一个夹角,12条折痕共形成13个夹角,每个夹角的度数是9°,则折扇左右两个木条的夹角是9°×13。
【详解】9°×(12+1)
=9°×13
=117°
答:这把折扇左右两个木条的夹角度数是117°。
【点睛】本题关键是明确夹角数量=折痕数+1,据此求出总的夹角数量,再乘每个夹角度数即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.5角的度量(一)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.图中所有锐角的和是90°,那么∠AOB是( )。
A.15° B.30° C.45°
2.任意两个锐角的度数之和,与直角的度数相比,( )。
A.等于直角的度数 B.比直角的度数大
C.比直角的度数小 D.不确定
3.从3时到8时,时针旋转了( )。
A.120° B.150° C.170°
4.估一估,如图中台灯灯秆夹角大约是( )。
A.60° B.90° C.120° D.160°
5.下面说法正确的是( )。
A.射线是直线的一部分,所以射线比直线短。
B.把一个30度的角放在10倍放大镜下观察,角变成300°。
C.一个九位数,它的最高位的计数单位是亿位。
D.在6和7之间添上7个0,这个数才能成为六亿零七。
6.放风筝比赛时,规定用30米长的线,如果把每根风筝线的一端固定在地面上,风筝线和地面所形成的角如图,风筝( )放得最高。
A.① B.② C.③ D.不确定
7.把一个50°的角两边分别延长,得到的角的度数是( )。
A.100° B.50° C.不能确定
8.比一比,( )角大。
A.左边的 B.右边 C.一样 D.无法比较
9.20°的角中包含( )个1°的角。
A.20 B.10 C.45 D.2
10.下列情况中,角会变大的是( )。
A.用放大镜看角 B.把角的两边画得更长 C.让角的开口张大一些
二、填空题
11.分一分。
1° 15° 134° 78° 110° 23° 89°
锐角: ;
钝角: 。
12.钟面上,( )时整,时针与分针所成的角是平角,( )时整,时针与分针所成的角是周角。
13.钟表上的时间为10:50时,时针与分针形成的较小夹角是( )度。
14.一个角比直角大25°,它的度数是( ),它是( )角;一个角比直角小32°,它的度数是( ),它是( )角。
15.把一个半圆平均分成4份,每一份是( )度。
16.图中,直线和的位置关系是( ),直线和的位置关系是( ),直线和的位置关系是( ),,那么( )。
17.先分别写出每个时刻时针与分针的夹角是什么角,再写出它们的度数。
( )角 ( )角 ( )角 ( )角 ( )角
( )°( )°( )°( )°( )°
18.一小时,时针走( )°。
19.写出时针与分针所形成的角的名称。
( ) ( ) ( )
20.写出下面每个角的度数。
( ) ( ) ( )
三、判断题
21.两个锐角的和一定是钝角。( )
22.用放大3倍的放大镜看一个40°的角,看到的角是120°。( )
23.30°的角比20°的角大。( )
24.2:30到2:50,分针走了120°。( )
25.72°的角比68°的角小。( )
四、计算题
26.求∠1、∠2、∠3的度数。
五、解答题
27.数一数,说一说,比较下面,,的大小。
28.看图,奇思想做一个什么学具?做好了会看到哪些图形?还会想到什么?
29.已知,求∠2,∠3是多少度?
30.折一折,想一想。
已知∠1=30°,求∠2的度数。
31.下面是一把打开后的折扇,每相邻两条折痕的夹角的度数都是9°,不算两边,一共有12条折痕,这把折扇左右两个木条的夹角度数是多少?(木条与折痕的夹角也是9°)
《2.5角的度量(一)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C D A B C A C
1.C
【分析】解决本题时应先明确图中的锐角分别是哪几个角,进而明确这些锐角之间的关系,再进一步解答即可。如图所示,图中的锐角共3个,即∠AOC、∠COB和∠AOB。∠AOC+∠COB+∠AOB=90°,而∠AOC+∠COB=∠AOB,则∠AOB=90°÷2。
【详解】
∠AOB=90°÷2=45°
故答案为:C
2.D
【分析】锐角是指大于0°且小于90°的角,两个锐角之和有可能大于90°,也有可能小于90°,也有可能等于90°。
【详解】假如两个锐角是30°和40°,和就是70°,比直角度数小;假如两个锐角是70°和30°,和就是100°,比直角度数大;假如两个锐角分别都是45°,那么相加之和就等于直角度数。所以答案不确定。
故答案为:D
3.B
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°。从3时到8时,时针走了5个大格,旋转了5×30°。
【详解】5×30°=150°,从3时到8时,时针旋转了150°。
故答案为:B
【点睛】明确钟面上每个大格是30°,这是解决本题的关键。
4.C
【分析】观察图形可知,台灯灯杆夹角是一个钝角,所以,排除A、B,但是这个角的大小更接近直角,所以排除D,选择C即可。
【详解】根据分析可知,图中台灯灯杆夹角大约是120°。
故答案为:C
5.D
【分析】直线没有端点,可以向两端无限延伸,不能度量长度;射线有一个端点,可以向一端无限延伸,不能度量长度;
角的大小与两条边的长短无关,只与角两条边张开的大小有关;
从右边起,亿位在第九位,它的计数单位是“亿”;
读亿以上的数时,先读亿级,再读万级,最后读个级,亿级、万级的数要按照个级的数的读法来读,再在末尾加上“亿”、“万”,每级末尾不管有几个0,都不读,其余数位有一个0或连续几个0,都只读一个。据此解答。
【详解】A.由分析可知,直线和射线都不能度量长度,所以无法比较它们的长度关系,选项错误;
B.把角放在放大镜下观看,放大的角两边的长度,角两边张开大小不变,角的大小不变,选项错误;
C.由分析可知,九位数的最高位是亿位,计数单位是“亿”,选项错误;
D.6和7之间添上7个0,这个数变成600000007,读作六亿零七,选项正确。
故答案为:D
6.A
【分析】因为线的长度是固定的都是30米,所以谁与地面的夹角接近90度,谁的高度就高;观察上图可知,三条线中,①与地面的夹角最接近90度,所以①放的最高,据此解答。
【详解】根据分析得:①与地面的夹角最接近90度,所以①放的最高。
故答案为:A
7.B
【分析】把一个角两边分别延长,但没有改变角两边叉开的大小,则角的度数不变。
【详解】把一个50°的角两边分别延长,得到的角的度数是50°。
故答案为:B
【点睛】角的大小跟两边叉开的大小有关,跟边的长短无关。
8.C
【分析】观察上图可知,两个角都是直角,一样大,据此即可解答。
【详解】根据分析可知,两个角一样大。
故答案为:C
【点睛】本题主要考查学生对角的分类知识的掌握和灵活运用。
9.A
【分析】根据求一个数里面有几个另一个数,用除法列式计算即可。
【详解】20°÷1°=20(个),则20°的角中包含20个1°的角。
胡答案为:A
【点睛】一个角度数是几度,就包含几个1°的角。
10.C
【分析】角的大小取决于组成角的两条边张开的程度,张开的越大,角就越大,张开的越小,角就越小,与边的长短无关,放大镜不能改变角的两边张开的大小,因此不能改变角的度数,据此解答即可。
【详解】由题意经过分析,用放大镜看角和把角的两边画得更长,都不能改变角的大小,让角的开口张大一些可以使角变大。
故答案为:C
11. 1°、15°、78°、 23°、 89° 134°、110°
【分析】大于0°小于90°的角叫做锐角,大于90°小于180°的角叫做钝角,据此解答。
【详解】锐角:1°、15°、78°、 23°、 89°
钝角:134°、110°
【点睛】熟练掌握锐角和钝角的定义是解决本题的关键。
12. 6 12
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°。整时,分针指向12,要使时针和分针成平角,即180°,则分针指向6。要使分针与时针成周角,即360°,时针应指向12。
【详解】6×30°=180°,12×30°=360°
钟面上,6时整,时针与分针所成的角是平角,12时整,时针与分针所成的角是周角。
【点睛】本题考查钟面问题,明确钟面上每个大格是30°,这是解决本题的关键。
13.25
【分析】钟面上每相邻两个数字间的夹角是:360°÷12=30°,50分钟是1小时的,10:50时,分针指在10的位置,而时针走了两个数字之间(10和11之间)的,此时时针和分针的夹角是(30÷6×5)°。据此解答。
【详解】360°÷12=30°
50分钟是1小时的;
30°÷6×5
=5°×5
=25°
【点睛】本题考查的是求时针与分针夹角的问题,关键是明确时针走到10和11之间的什么位置。
14. 115° 钝 58° 锐
【分析】直角的度数为90°,一个角比直角大25°,它的度数用加法计算即可;一个角比直角小32°,它的度数用减法计算即可;大于90°,小于180°的角为钝角;大于0°,小于90°的角为锐角。
【详解】由于90°+25°=115°,180°>115°>90°;
90°-32°=58°,0°<58°<90°;
所以一个角比直角大25°,它的度数是115°,它是钝角;一个角比直角小32°,它的度数是58°,它是锐角。
【点睛】本题主要考查了角的分类及大小关系。
15.45
【分析】半圆也就是180度,把半圆平均分成4份,180度除以4等于一份的度数,据此即可解答。
【详解】180°÷4=45°
把一个半圆平均分成4份,每一份是45度。
【点睛】熟练掌握角的度数的表示方法是解答本题的关键。
16. 平行/互相平行 垂直/互相垂直 相交 119
【分析】在同一平面内,不相交的两条直线互相平行,其中一条直线是另一条直线的平行线;两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫做垂足。据此判断几条直线的位置关系。由图可知,∠1和∠2组成了一个平角。∠1=61°,那么直接用180°减去61°即可算出∠2的度数。
【详解】由图可知,直线a和b没有交点,所以这两条直线互相平行。直线a和c相交成直角,所以这两条直线互相垂直。直线b和d有交点,所以这两条直线相交。
∠2=180°-∠1=180°-61°=119°
直线和的位置关系是平行,直线和的位置关系是垂直,直线和的位置关系是相交,,那么119°。
17. 平 钝 周 锐 直 180 120 360 60 90
【分析】时钟上12个数字把钟面平均分成12个大格,每个大格是30°。钟面上6时整,时针和分针之间有6个大格,则时针和分针的夹角是6×30°。钟面上8时整,时针和分针之间有4个大格,则时针和分针的夹角是4×30°。钟面上12时整,时针和分针之间有12个大格,则时针和分针的夹角是12×30°。钟面上2时整,时针和分针之间有2个大格,则时针和分针的夹角是2×30°。钟面上3时整,时针和分针之间有3个大格,则时针和分针的夹角是3×30°。再明确各个角的类型。
【详解】6×30°=180°
4×30°=120°
12×30°=360°
2×30°=60°
3×30°=90°
【点睛】本题考查角的度量和角的分类,明确钟面上每个大格是30°,这是解决本题的关键。
18.30
【分析】钟面上有12大格,每一大格对应的角是30度,一小时,时针走一大格,即走30°据此即可解答。
【详解】根据分析可知,一小时,时针走30°。
【点睛】熟练掌握钟面的相关知识是解答本题的关键。
19. 钝角 锐角 直角
【分析】钟面上有12个大格,每两个大格之间的夹角是30°,4时整时,时针和分针之间有4个大格,利用4×30°=120°,这是一个钝角;10时整时,时针和分针之间有2个大格,就用2×30°=60°,这是一个锐角;9时整时,时针和分针之间有3个大格,就用3×30°=90°,这是一个直角。
【详解】根据分析可知:
【点睛】本题考查了钟面角的认识,关键明白钟面上有12个大格,两个大格之间的夹角是30°。
20.
【分析】已知每个测量单位的度数是,分别数一数每个图中的大角中有几个单位,用测量单位的数量乘,据此可求出每个角的度数。
【详解】
第一个角是,第二个角是,第三角是。
21.×
【分析】小于90°的角叫做锐角,两个锐角的和小于180°,可能是锐角、直角或者钝角,据此判断。
【详解】例如10°+20°=30°,40°+50°=90°,60°+70°=130°,两个锐角的和可能是锐角、直角或者钝角,说法错误。
故答案为:×
【点睛】本题关键是熟记锐角、直角和钝角的定义,采用举反例的方法解答。
22.×
【分析】角的大小与角两边的长短无关,只与角开叉的大小有关,开叉越大,角就越大,据此即可解答。
【详解】用放大3倍的放大镜看一个40°的角,看到的角比原角的两边要长,但角的开叉大小没变,所以看到的角还是40°,原说法错误。
故答案为:×
【点睛】本题主要考查学生对影响角的大小因素的掌握和灵活运用。
23.√
【分析】比较两个角度数的大小,直接比较单位“°”前面数字的大小即可。
【详解】30°>20°,则30°的角比20°的角大。题干说法正确。
故答案为:√
【点睛】本题考查角的大小比较,需熟练掌握。
24.√
【分析】根据经过时间=结束时间-开始时间,可知从2:30到2:50,经过了20分钟。时钟上12个数字把钟面平均分成12个大格,每个大格是30°。经过20分钟则分针走4个大格,共走了4×30°。
【详解】2时50分-2时30分=20(分钟)
4×5=20(分钟)
4×30°=120°
则2:30到2:50,分针走了120°。
故答案为:√
【点睛】本题考查钟表问题,明确钟面上每个大格是30°,是解决本题的关键。
25.×
【分析】根据角的度数比较角的大小,度数越大的角就越大。
【详解】72°>68°,所以72°的角比68°的角小。
故答案为:×
【点睛】本题考查的是角的大小比较。
26.∠1=155°;∠2=65°;∠3=25°
【分析】观察可知,∠1与25°组成了一个平角(180°),那么∠1=180°-25°;∠1与∠3组成了一个平角,那么∠3=180°-∠1;∠2与∠3组成了一个直角(90°),那么∠2=90°-∠3。据此解答。
【详解】∠1=180°-25°=155°
∠3=180°-∠1=180°-155°=25°
∠2=90°-∠3=90°-25°=65°
27.∠3>∠2>∠1
【分析】结合所给图形,首先数出每个角中小刻度的个数,再根据角的大小与叉开的角度有关。结合每个角中小刻度的个数即可得出其答案。
【详解】∠1张开的角度是11个小刻度,∠2张开的角度是12个小刻度,∠3张开的角度是13个小刻度。因为每个刻度都相等,13>12>11,所以∠3>∠2>∠1。
28.见详解
【分析】从一点引出两条射线所形成的图形叫做角。这一点是角的顶点,两条射线是角的边。小于90°的角是锐角,90°的角叫做直角,大于90°小于180°的角叫做钝角,180°的角叫做平角,360°的角叫做周角,据此解答。
【详解】根据题目给出的信息可知,奇思想做一个关于角的学具,做好后会看到锐角、直角、钝角、平角和周角。能想到:角的大小跟两边叉开的大小有关,跟边的长短无关。
29.∠2=45°;∠3=45°
【分析】∠1与∠3组成了一个直角,那么∠3=90°-∠1;∠2与135°组成了一个平角,那么∠2=180°-135°。
【详解】∠3=90°-45°=45°
∠2=180°-135°=45°
【点睛】解答本题的关键是掌握直角等于90°,平角等于180°。
30.75°
【分析】
如图所示,将长方形纸折一折,得到的∠2=∠3,∠1、∠2和∠3组成一个平角,则∠2=(180°-∠1)÷2。
【详解】∠2=(180°-∠1)÷2=(180°-30°)÷2=150°÷2=75°
【点睛】解决此类问题时,要善于利用图中隐藏的特殊角(直角、平角、周角),以及它与各角之间的关系,利用已知角,求出未知角。
31.117°
【分析】每相邻两条折痕形成一个夹角,12条折痕共形成13个夹角,每个夹角的度数是9°,则折扇左右两个木条的夹角是9°×13。
【详解】9°×(12+1)
=9°×13
=117°
答:这把折扇左右两个木条的夹角度数是117°。
【点睛】本题关键是明确夹角数量=折痕数+1,据此求出总的夹角数量,再乘每个夹角度数即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
