4.4乘法结合律暑假预习练 (含解析) 北师大版数学四年级上册
文档属性
| 名称 | 4.4乘法结合律暑假预习练 (含解析) 北师大版数学四年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 09:55:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
4.4乘法结合律
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.与45×6×11的积相等的算式是( )。
A.45×6+11 B.11×(6×45) C.(45+6)×11
2.简算4×127×2.5=127×(4×2.5),用到的运算定律是( )
A.乘法结合律和乘法分配律
B.乘法分配律和乘法交换律
C.乘法交换律和乘法结合律
3.25×8×4×125=(25×4)×(8×125)这是运用了( )。
A.乘法交换律 B.乘法结合律
C.乘法交换律和结合律 D.加法结合律
4.2473+(6000-2632)= ( )
A.4862 B.5841 C.4702 D.4802
5.在计算23×25×4时,先算( )比较简便。
A.23×25 B.25×4 C.23×4
6.下列选项中,( )应用了乘法结合律。
A.(a+b)+c=a+(b+c) B.(4×3)×3=4×(3×3) C.a×b=b×a
7.3×4×5=3×(4×5)这样子计算( )。
A.正确 B.错误
8.计算44×25时,运用乘法结合律,最合理的简便方法是( )。
A.4×25×11 B.40×25+4×25
C.(4×5)×(11×5) D.44×5×5
9.用简便方法计算,选出正确答案.
=( )
A.0 B.1 C.2 D.
10.下面的算法应用了( )。
A.乘法结合律 B.加法交换律
C.乘法分配律 D.加法结合律
二、填空题
11.运用运算律在里填一填。
( + )+( + ) ( × )×
12.如果☆×△=45,那么(☆×104)×△=( );如果☆×△=60,那么(☆×4)×(△×5)=( )。
13.在□内填上合适的数,在○内填上合适的运算符号,并在横线上写出运用的运算律。
()运用了 。
()运用了 。
运用了 。
14.在括号里填上“>”“<”或“=”。
964370( )112087000 49亿( )499000000
240×30( )300×24 35×2×5( )35×(2×5)
15.运用乘法交换律和乘法结合律填空。
26×5×2=26×( × ) 78×125× = ×( ×8)
(29×25)×4=29×( × ) 400× ×8=400×(75×8)
16×125=2×( ×125) 25×24=( × )×6
25×125×4×80=( × )×( × )
16.已知12345679×9=111111111,那么12345679×54= .
17.计算.
34× +34× = .
18.三个数相乘,先把( )相乘,再和( )相乘;或者先把 ( )相乘,再和( )相乘,它们的结果不变,这叫做( ).用字母表示为( ).
19.56×8×125=56×(8×125),运用了乘法( )律;45+98+55=45+55+98,运用了加法( )律。(填“交换”“结合”或“分配”)
20.在横线上填合适的数。
(1)72×4×5=72×(4× )
(2)(3×8)×125=( × )×3
(3)3×4×25=( × )×
(4)125×5×8×20=( × )×( × )
三、判断题
21.24×25=6×(4×25)。( )
22.乘法的交换律和乘法结合律可以同时应用。 ( )
23.乘法结合律和乘法交换律能同时使用。( )
24.(45×a)×19=45×(a×19)。( )
25.25×13×4=13×(25×4)运用了乘法交换律和结合律。( )
四、计算题
26.简算。
125×99×8 32×25×4
3600÷25÷4 5×49×20
27.淘气是这样计算的。
(1)你能看懂吗?和同伴交流你的想法。
(2)试着运用乘法交换律和乘法结合律计算下面各题。
五、解答题
28.一个书架能摆56本书,25个这样的书架一共有多少本书?
29.学校买来4箱图书,每箱36本,每本25元。这些书一共多少元?
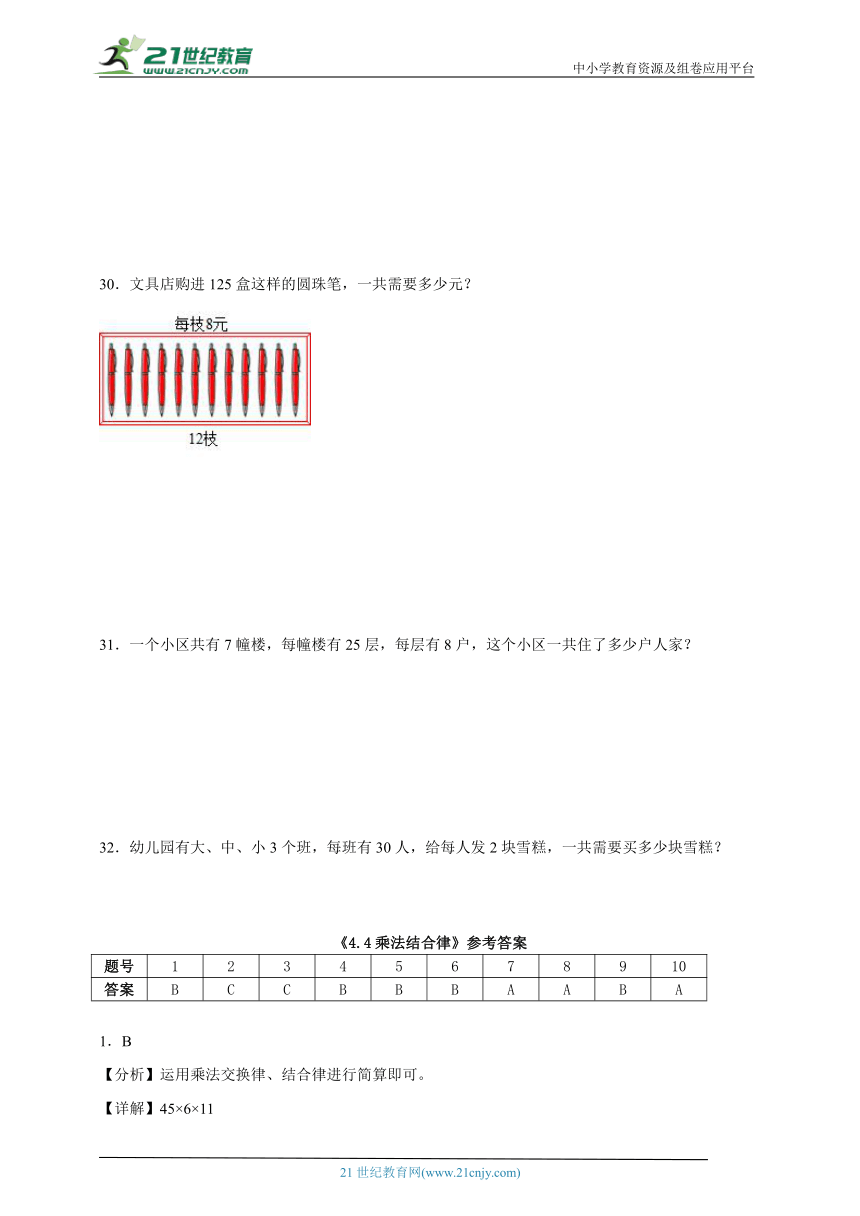
30.文具店购进125盒这样的圆珠笔,一共需要多少元?
31.一个小区共有7幢楼,每幢楼有25层,每层有8户,这个小区一共住了多少户人家?
32.幼儿园有大、中、小3个班,每班有30人,给每人发2块雪糕,一共需要买多少块雪糕?
《4.4乘法结合律》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C B B B A A B A
1.B
【分析】运用乘法交换律、结合律进行简算即可。
【详解】45×6×11
=11×6×45
=11×(6×45)
故答案为:B
【点睛】本题主要考查了乘法的交换律和结合律。
2.C
【解析】乘法运算:
①乘法交换律:两个因数交换位置,积不变.如a×b=b×a.
②乘法结合律:先乘前两个数,或先乘后两个数,积不变.如a×b×c=a×(b×c);据此解答即可,
【详解】4×127×2.5
=127×(4×2.5)
所以简算4×127×2.5时,要用到的运算定律是乘法交换律和乘法结合律;
故选:C.
【点睛】此题重点考查了学生对乘法交换律和结合律的掌握与运用情况.
3.C
【分析】乘法交换律:两个数相乘,交换两个因数的位置,积不变。乘法结合律:三个数相乘,先把前两个数相乘或先把后两个数相乘,积不变。根据乘法交换律和乘法结合律的定义进行分析即可。
【详解】根据分析可得:
25×8×4×125
=25×4×8×125(乘法交换律)
=(25×4)×(8×125)(乘法结合律)
=100×1000
=100000
故答案为:C。
【点睛】本题考查了利用运算定律进行简便运算,要熟练掌握。
4.B
【分析】算式中含有小括号,要先算小括号里面的减法,再算小括号外面的加法.
【详解】2473+(6000-2632)
=2473+3368
=5841
故答案为B
5.B
【分析】根据乘法结合律,先计算25×4,得到100,再乘23,据此进行简算。
【详解】23×25×4
=23×(25×4)
=23×100
=2300
则先算25×4比较简便。
故答案为:B
【点睛】本题考查乘法结合律的掌握和应用,乘法结合律不改变因数的位置,改变运算顺序。
6.B
【点睛】三个数相乘,先把前两个数相乘,或先把后两个数相乘,它们的积不变.可用字母a,b,c来表示这三个数:(a×b)×c=a×(b×c);根据加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加。和不变,这叫做加法结合律。用字母表示为(a+b)+c=a+(b+c);乘法交换律就是把两个数交换位置,据此判断。
【详解】A.运用了加法结合律,不符合题意;
B.运用了乘法结合律,符合题意;
C.运用了乘法交换律,不符合题意。
故答案为:B
7.A
【分析】乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。
【详解】根据分析可知,
3×4×5=3×(4×5)这样子计算正确。
故答案为:A
【点睛】熟练掌握乘法结合律的定义是解答此题的关键。
8.A
【分析】因为4×25=100,所以计算44×25时,先把44分解成4×11,然后再把4和25结合在一起先计算,据此解答。
【详解】44×25
=(4×11)×25
=4×11×25
=100×11
=1100
所以把把44×25变成4×25×11,是最简便合理的方法。
故答案为:A
【点睛】在乘法的简算中,明确4×25=100是解答本题的关键。
9.B
【分析】可以先去掉括号,由于括号前面是减号,所以要改变括号内的运算符号,然后按照从左到右的顺序计算,这样计算比较简便.
【详解】
=
=
=1
故答案为B
10.A
【分析】三个数相乘,先把前两个数相乘,再乘第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c)。据此解答即可。
【详解】由分析可知:算法应用了乘法结合律。
故答案为:A
11. 15 85 34 66 25 4 77
【分析】第1题,根据加法结合律填空;第2题,根据乘法结合律填空。
【详解】15+34+85+66=(15+85)+(34+66)
(25×77)×4=(25×4)×77
【点睛】加法结合律:(a+b)+c=a+(b+c),乘法结合律:(a×b)×c=a×(b×c)。
12. 4680 1200
【分析】将括号拆开,然后根据乘法的交换律和乘法结合律的特点进行计算即可。
乘法结合律的特点是三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
乘法交换律的特点是两个数相乘,交换两个因数的位置,积不变。
【详解】(☆×104)×△
=☆×104×△
=☆×△×104
=45×104
=4680
(☆×4)×(△×5)
=☆×4×△×5
=(☆×△)×(4×5)
=60×20
=1200
【点睛】熟练掌握乘法结合律与乘法交换律的特点是解答此题的关键。
13.82;+;18;加法交换律、加法结合律;
8;×;5;乘法结合律;
×;17;乘法交换律
【分析】根据加法交换律:,两数相加,交换两个加数的位置,和不变;
加法结合律:,三个数相加,先把前两个数相加,再和第三个数相加,或者先把后两个数相加,再和第一个相加,和不变;
乘法交换律:,交换两个乘数的位置,积不变;
乘法结合律:,三个数相乘,先把前两个数相乘,再和第三个数相乘,或者先把后两个数相乘,再和第一个相乘,积不变,据此解答。
【详解】()运用了加法交换律、加法结合律。
()运用了乘法结合律。
运用了乘法交换律。
14. < > = =
【分析】(1)(2)比较整数的大小,先看数位的多少,数位多的数就大,数位相同,从高位比较,高位上的数大则这个数大,高位上的数相同,就比较下一位,以此类推;
(3)积不变的规律:两个数相乘,一个因数乘(或除以)一个数(0除外),另一个因数同时除以(或乘)相同的数,它们的积不变;
(4)乘法结合律:三个数相乘,先把前两个数相乘或先把后两个数相乘,积不变;用字母表示为:(a×b)×c=a×(b×c);据此解答即可。
【详解】964370<112087000
因为49亿=4900000000,4900000000>499000000,所以49亿>499000000;
因为(240÷10)×(30×10)=24×300,所以240×30=300×24;
因为35×2×5=35×(2×5)=35×10=350,所以35×2×5=35×(2×5)。
15. 5 2 8 78 125 25 4 75 8 25 4 25 4 125 80
【分析】乘法交换律是指交换乘法中因数的位置,而不改变积的大小;乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变,据此作答。
【详解】根据上述分析可得:
26×5×2=26×(5×2),利用了乘法结合律;
78×125×8=78×(125×8),利用了乘法结合律;
(29×25)×4=29×(25×4),利用了乘法结合律;
400×75×8=400×(75×8),利用了乘法结合律;
16×125=2×(8×125),将16拆分为2×8,利用了乘法结合律;
25×24=(25×4)×6,将24拆分为4×6,利用了乘法结合律;
25×125×4×80=(25×4)×(125×80),利用了乘法交换律和乘法结合律。
16.666666666
【分析】因为12345679×9=111111111,所以12345679×54=12345679×9×6=111111111×6=666666666;据此解答即可.
【详解】12345679×54 =12345679×9×6
=111111111×6
=666666666;
故答案为666666666.
17.34
【分析】此题可以运用乘法分配律,用34乘两个分数的和,这样计算比较简便.
【详解】
=
=34
故答案为34
18. 前两个数 第三个数 后两个数 第一个数 乘法结合律 (ab)c=a(bc)
【详解】略
19. 结合 交换
【分析】根据乘法结合律的定义:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变;根据加法交换律,可得两个数相加,交换加数的位置,和不变,这叫加法交换律,由此进行填空即可。
【详解】56×8×125=56×(8×125),运用了乘法结合律;45+98+55=45+55+98,运用了加法交换律。
【点睛】本题主要考查了学生对运算定律的熟练掌握情况,牢记定律内容是解答本题的关键。
20. 5 8 125 4 25 3 125 8 5 20
【分析】根据乘法交换律和结合律进行解答即可。
【详解】(1)72×4×5=72×(4×5)
(2)(3×8)×125=(8×125)×3
(3)3×4×25=(4×25)×3
(4)125×5×8×20=(125×8)×(5×20)
【点睛】乘法交换律:两个数相乘,交换乘数的位置,它们的积不变,多个数依然通用;乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。要牢记这两个运算律。
21.√
【分析】可以将24看作是6和4相乘,然后先算4和25相乘,运用了乘法结合律。
【详解】24×25
=6×4×25
=6×(4×25)
所以判断正确。
【点睛】本题考查了学生对于乘法结合律的灵活运用。
22.√
【分析】乘法交换律和结合律可以同时应用,举例说明,即可解答。
【详解】如:25×32×4
=32×(25×4)
=32×100
=3200
所以乘法交换律和结合律可以同时应用。
故答案为:√
【点睛】本题考查乘法交换律和结合律可以同时应用。
23.√
【分析】乘法结合律和乘法交换律可以同时使用,可举例说明。
【详解】例如:
8×38×125
=38×(8×125)
=38×1000
=38000
其中第一步就是乘法交换律和乘法结合律同时使用。
所以乘法结合律和乘法交换律能同时使用。
故答案为:√
【点睛】熟练掌握乘法结合律和乘法交换律的定义是解答此题的关键。
24.√
【分析】乘法结合律:(a×b)×c=a×(b×c);据此即可解答。
【详解】根据乘法结合律,(45×a)×19=45×(a×19),原等式成立。
故答案为:√
【点睛】熟练掌握乘法结合律是解答本题的关键。
25.√
【分析】计算25×13×4时,交换因数25和13的位置,运用了乘法交换律,此时算式为13×25×4,应先计算13×25,而算式13×(25×4)先计算25×4,运用了乘法结合律。
【详解】根据分析可知,25×13×4=13×(25×4)运用了乘法交换律和结合律。
故答案为:√。
【点睛】本题考查乘法交换律和乘法结合律,需熟练掌握并能灵活运用。
26.99000;3200
36;4900
【分析】(1)利用乘法交换律进行简算;(2)利用乘法结合律进行简算;
(3)利用除法的性质进行简算;(4)利用乘法交换律进行简算。
【详解】125×99×8
=125×8×99
=1000×99
=99000
32×25×4
=32×(25×4)
=32×100
=3200
3600÷25÷4
=3600÷(25×4)
=3600÷100
=36
5×49×20
=5×20×49
=100×49
=4900
27.(1)见详解;
(2)8000;100000
【分析】(1)淘气首先将24拆分为6和4两个数的乘积,然后将4和25相乘得到100,最后将6和100相乘得到600。这个过程中,淘气运用了乘法结合律,使得计算过程更加简便。
(2)首先将64拆分为8和8两个数的乘积,然后将8和125相乘得到1000,最后将8和1000相乘得到 8000。首先将32拆分为8和4两个数的乘积,然后将125和8相乘得到1000,再将25和4相乘得到100,最后将1000和100相乘得到100000。
【详解】(1)因为4×25=100,24=4×6, 利用乘法结合律可以得到: 24×25 =6×4×25 =6×(4×25) =6×100 =600
(2)64×125
=8×8×125
=8×(8×125)
=8×1000
=8000
125×25×32
=125×25×8×4
=(125×8)×(25×4)
=1000×100
=100000
28.1400本
【分析】用每个书架能摆的本数乘书架的个数,把56拆分成4×14,然后运用乘法交换律简便计算即可。
【详解】56×25
=4×14×25
=4×25×14
=100×14
=1400(本)
答:一共有1400本书。
【点睛】考查用乘法解决实际问题。注意计算过程可以利用运算定律进行简便运算。
29.3600元
【分析】先求出4箱图书的总本数,用36乘4,1本25元,再用所得积乘25,计算时可以根据乘法结合律,先求出25与4的积,再乘36。
【详解】36×4×25
=36×(4×25)
=36×100
=3600(元)
答:一共要3600元。
【点睛】熟练掌握乘法结合律在解决实际问题中应用。
30.12000元
【分析】每盒有12支,用12乘8,求出购买1盒这样的圆珠笔需要的钱数,再乘125,求出一共需要多少元;因为8×125=1000,可以根据乘法结合律进行简算。
【详解】12×8×125
=12×(8×125)
=12×1000
=12000(元)
答:一共需要12000元。
【点睛】本题主要考查了学生对乘法结合律的掌握与灵活运用。
31.1400户
【分析】小区总共的幢数乘每幢楼的层数等于总共的层数,再乘每层的户数即可解答。
【详解】7×25×8
=7×(25×8)
=7×200
=1400(户)
答:这个小区一共住了1400户人家。
【点睛】本题主要考查学生对乘法结合律的掌握和灵活运用。
32.180块
【分析】可以先算出每个班发多少块雪糕,列式为30×2,然后再算3个班一共需要买多少块雪糕,列式为30×2×3,据此解答。
【详解】30×2×3
=60×3
=180(块)
答:一共需要买180块雪糕。
【点睛】本题考查了学生运用连乘解决实际问题的能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.4乘法结合律
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.与45×6×11的积相等的算式是( )。
A.45×6+11 B.11×(6×45) C.(45+6)×11
2.简算4×127×2.5=127×(4×2.5),用到的运算定律是( )
A.乘法结合律和乘法分配律
B.乘法分配律和乘法交换律
C.乘法交换律和乘法结合律
3.25×8×4×125=(25×4)×(8×125)这是运用了( )。
A.乘法交换律 B.乘法结合律
C.乘法交换律和结合律 D.加法结合律
4.2473+(6000-2632)= ( )
A.4862 B.5841 C.4702 D.4802
5.在计算23×25×4时,先算( )比较简便。
A.23×25 B.25×4 C.23×4
6.下列选项中,( )应用了乘法结合律。
A.(a+b)+c=a+(b+c) B.(4×3)×3=4×(3×3) C.a×b=b×a
7.3×4×5=3×(4×5)这样子计算( )。
A.正确 B.错误
8.计算44×25时,运用乘法结合律,最合理的简便方法是( )。
A.4×25×11 B.40×25+4×25
C.(4×5)×(11×5) D.44×5×5
9.用简便方法计算,选出正确答案.
=( )
A.0 B.1 C.2 D.
10.下面的算法应用了( )。
A.乘法结合律 B.加法交换律
C.乘法分配律 D.加法结合律
二、填空题
11.运用运算律在里填一填。
( + )+( + ) ( × )×
12.如果☆×△=45,那么(☆×104)×△=( );如果☆×△=60,那么(☆×4)×(△×5)=( )。
13.在□内填上合适的数,在○内填上合适的运算符号,并在横线上写出运用的运算律。
()运用了 。
()运用了 。
运用了 。
14.在括号里填上“>”“<”或“=”。
964370( )112087000 49亿( )499000000
240×30( )300×24 35×2×5( )35×(2×5)
15.运用乘法交换律和乘法结合律填空。
26×5×2=26×( × ) 78×125× = ×( ×8)
(29×25)×4=29×( × ) 400× ×8=400×(75×8)
16×125=2×( ×125) 25×24=( × )×6
25×125×4×80=( × )×( × )
16.已知12345679×9=111111111,那么12345679×54= .
17.计算.
34× +34× = .
18.三个数相乘,先把( )相乘,再和( )相乘;或者先把 ( )相乘,再和( )相乘,它们的结果不变,这叫做( ).用字母表示为( ).
19.56×8×125=56×(8×125),运用了乘法( )律;45+98+55=45+55+98,运用了加法( )律。(填“交换”“结合”或“分配”)
20.在横线上填合适的数。
(1)72×4×5=72×(4× )
(2)(3×8)×125=( × )×3
(3)3×4×25=( × )×
(4)125×5×8×20=( × )×( × )
三、判断题
21.24×25=6×(4×25)。( )
22.乘法的交换律和乘法结合律可以同时应用。 ( )
23.乘法结合律和乘法交换律能同时使用。( )
24.(45×a)×19=45×(a×19)。( )
25.25×13×4=13×(25×4)运用了乘法交换律和结合律。( )
四、计算题
26.简算。
125×99×8 32×25×4
3600÷25÷4 5×49×20
27.淘气是这样计算的。
(1)你能看懂吗?和同伴交流你的想法。
(2)试着运用乘法交换律和乘法结合律计算下面各题。
五、解答题
28.一个书架能摆56本书,25个这样的书架一共有多少本书?
29.学校买来4箱图书,每箱36本,每本25元。这些书一共多少元?
30.文具店购进125盒这样的圆珠笔,一共需要多少元?
31.一个小区共有7幢楼,每幢楼有25层,每层有8户,这个小区一共住了多少户人家?
32.幼儿园有大、中、小3个班,每班有30人,给每人发2块雪糕,一共需要买多少块雪糕?
《4.4乘法结合律》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C B B B A A B A
1.B
【分析】运用乘法交换律、结合律进行简算即可。
【详解】45×6×11
=11×6×45
=11×(6×45)
故答案为:B
【点睛】本题主要考查了乘法的交换律和结合律。
2.C
【解析】乘法运算:
①乘法交换律:两个因数交换位置,积不变.如a×b=b×a.
②乘法结合律:先乘前两个数,或先乘后两个数,积不变.如a×b×c=a×(b×c);据此解答即可,
【详解】4×127×2.5
=127×(4×2.5)
所以简算4×127×2.5时,要用到的运算定律是乘法交换律和乘法结合律;
故选:C.
【点睛】此题重点考查了学生对乘法交换律和结合律的掌握与运用情况.
3.C
【分析】乘法交换律:两个数相乘,交换两个因数的位置,积不变。乘法结合律:三个数相乘,先把前两个数相乘或先把后两个数相乘,积不变。根据乘法交换律和乘法结合律的定义进行分析即可。
【详解】根据分析可得:
25×8×4×125
=25×4×8×125(乘法交换律)
=(25×4)×(8×125)(乘法结合律)
=100×1000
=100000
故答案为:C。
【点睛】本题考查了利用运算定律进行简便运算,要熟练掌握。
4.B
【分析】算式中含有小括号,要先算小括号里面的减法,再算小括号外面的加法.
【详解】2473+(6000-2632)
=2473+3368
=5841
故答案为B
5.B
【分析】根据乘法结合律,先计算25×4,得到100,再乘23,据此进行简算。
【详解】23×25×4
=23×(25×4)
=23×100
=2300
则先算25×4比较简便。
故答案为:B
【点睛】本题考查乘法结合律的掌握和应用,乘法结合律不改变因数的位置,改变运算顺序。
6.B
【点睛】三个数相乘,先把前两个数相乘,或先把后两个数相乘,它们的积不变.可用字母a,b,c来表示这三个数:(a×b)×c=a×(b×c);根据加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加。和不变,这叫做加法结合律。用字母表示为(a+b)+c=a+(b+c);乘法交换律就是把两个数交换位置,据此判断。
【详解】A.运用了加法结合律,不符合题意;
B.运用了乘法结合律,符合题意;
C.运用了乘法交换律,不符合题意。
故答案为:B
7.A
【分析】乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。
【详解】根据分析可知,
3×4×5=3×(4×5)这样子计算正确。
故答案为:A
【点睛】熟练掌握乘法结合律的定义是解答此题的关键。
8.A
【分析】因为4×25=100,所以计算44×25时,先把44分解成4×11,然后再把4和25结合在一起先计算,据此解答。
【详解】44×25
=(4×11)×25
=4×11×25
=100×11
=1100
所以把把44×25变成4×25×11,是最简便合理的方法。
故答案为:A
【点睛】在乘法的简算中,明确4×25=100是解答本题的关键。
9.B
【分析】可以先去掉括号,由于括号前面是减号,所以要改变括号内的运算符号,然后按照从左到右的顺序计算,这样计算比较简便.
【详解】
=
=
=1
故答案为B
10.A
【分析】三个数相乘,先把前两个数相乘,再乘第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c)。据此解答即可。
【详解】由分析可知:算法应用了乘法结合律。
故答案为:A
11. 15 85 34 66 25 4 77
【分析】第1题,根据加法结合律填空;第2题,根据乘法结合律填空。
【详解】15+34+85+66=(15+85)+(34+66)
(25×77)×4=(25×4)×77
【点睛】加法结合律:(a+b)+c=a+(b+c),乘法结合律:(a×b)×c=a×(b×c)。
12. 4680 1200
【分析】将括号拆开,然后根据乘法的交换律和乘法结合律的特点进行计算即可。
乘法结合律的特点是三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
乘法交换律的特点是两个数相乘,交换两个因数的位置,积不变。
【详解】(☆×104)×△
=☆×104×△
=☆×△×104
=45×104
=4680
(☆×4)×(△×5)
=☆×4×△×5
=(☆×△)×(4×5)
=60×20
=1200
【点睛】熟练掌握乘法结合律与乘法交换律的特点是解答此题的关键。
13.82;+;18;加法交换律、加法结合律;
8;×;5;乘法结合律;
×;17;乘法交换律
【分析】根据加法交换律:,两数相加,交换两个加数的位置,和不变;
加法结合律:,三个数相加,先把前两个数相加,再和第三个数相加,或者先把后两个数相加,再和第一个相加,和不变;
乘法交换律:,交换两个乘数的位置,积不变;
乘法结合律:,三个数相乘,先把前两个数相乘,再和第三个数相乘,或者先把后两个数相乘,再和第一个相乘,积不变,据此解答。
【详解】()运用了加法交换律、加法结合律。
()运用了乘法结合律。
运用了乘法交换律。
14. < > = =
【分析】(1)(2)比较整数的大小,先看数位的多少,数位多的数就大,数位相同,从高位比较,高位上的数大则这个数大,高位上的数相同,就比较下一位,以此类推;
(3)积不变的规律:两个数相乘,一个因数乘(或除以)一个数(0除外),另一个因数同时除以(或乘)相同的数,它们的积不变;
(4)乘法结合律:三个数相乘,先把前两个数相乘或先把后两个数相乘,积不变;用字母表示为:(a×b)×c=a×(b×c);据此解答即可。
【详解】964370<112087000
因为49亿=4900000000,4900000000>499000000,所以49亿>499000000;
因为(240÷10)×(30×10)=24×300,所以240×30=300×24;
因为35×2×5=35×(2×5)=35×10=350,所以35×2×5=35×(2×5)。
15. 5 2 8 78 125 25 4 75 8 25 4 25 4 125 80
【分析】乘法交换律是指交换乘法中因数的位置,而不改变积的大小;乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变,据此作答。
【详解】根据上述分析可得:
26×5×2=26×(5×2),利用了乘法结合律;
78×125×8=78×(125×8),利用了乘法结合律;
(29×25)×4=29×(25×4),利用了乘法结合律;
400×75×8=400×(75×8),利用了乘法结合律;
16×125=2×(8×125),将16拆分为2×8,利用了乘法结合律;
25×24=(25×4)×6,将24拆分为4×6,利用了乘法结合律;
25×125×4×80=(25×4)×(125×80),利用了乘法交换律和乘法结合律。
16.666666666
【分析】因为12345679×9=111111111,所以12345679×54=12345679×9×6=111111111×6=666666666;据此解答即可.
【详解】12345679×54 =12345679×9×6
=111111111×6
=666666666;
故答案为666666666.
17.34
【分析】此题可以运用乘法分配律,用34乘两个分数的和,这样计算比较简便.
【详解】
=
=34
故答案为34
18. 前两个数 第三个数 后两个数 第一个数 乘法结合律 (ab)c=a(bc)
【详解】略
19. 结合 交换
【分析】根据乘法结合律的定义:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变;根据加法交换律,可得两个数相加,交换加数的位置,和不变,这叫加法交换律,由此进行填空即可。
【详解】56×8×125=56×(8×125),运用了乘法结合律;45+98+55=45+55+98,运用了加法交换律。
【点睛】本题主要考查了学生对运算定律的熟练掌握情况,牢记定律内容是解答本题的关键。
20. 5 8 125 4 25 3 125 8 5 20
【分析】根据乘法交换律和结合律进行解答即可。
【详解】(1)72×4×5=72×(4×5)
(2)(3×8)×125=(8×125)×3
(3)3×4×25=(4×25)×3
(4)125×5×8×20=(125×8)×(5×20)
【点睛】乘法交换律:两个数相乘,交换乘数的位置,它们的积不变,多个数依然通用;乘法结合律:三个数相乘,先把前两个数相乘,再和另外一个数相乘,或先把后两个数相乘,再和另外一个数相乘,积不变。要牢记这两个运算律。
21.√
【分析】可以将24看作是6和4相乘,然后先算4和25相乘,运用了乘法结合律。
【详解】24×25
=6×4×25
=6×(4×25)
所以判断正确。
【点睛】本题考查了学生对于乘法结合律的灵活运用。
22.√
【分析】乘法交换律和结合律可以同时应用,举例说明,即可解答。
【详解】如:25×32×4
=32×(25×4)
=32×100
=3200
所以乘法交换律和结合律可以同时应用。
故答案为:√
【点睛】本题考查乘法交换律和结合律可以同时应用。
23.√
【分析】乘法结合律和乘法交换律可以同时使用,可举例说明。
【详解】例如:
8×38×125
=38×(8×125)
=38×1000
=38000
其中第一步就是乘法交换律和乘法结合律同时使用。
所以乘法结合律和乘法交换律能同时使用。
故答案为:√
【点睛】熟练掌握乘法结合律和乘法交换律的定义是解答此题的关键。
24.√
【分析】乘法结合律:(a×b)×c=a×(b×c);据此即可解答。
【详解】根据乘法结合律,(45×a)×19=45×(a×19),原等式成立。
故答案为:√
【点睛】熟练掌握乘法结合律是解答本题的关键。
25.√
【分析】计算25×13×4时,交换因数25和13的位置,运用了乘法交换律,此时算式为13×25×4,应先计算13×25,而算式13×(25×4)先计算25×4,运用了乘法结合律。
【详解】根据分析可知,25×13×4=13×(25×4)运用了乘法交换律和结合律。
故答案为:√。
【点睛】本题考查乘法交换律和乘法结合律,需熟练掌握并能灵活运用。
26.99000;3200
36;4900
【分析】(1)利用乘法交换律进行简算;(2)利用乘法结合律进行简算;
(3)利用除法的性质进行简算;(4)利用乘法交换律进行简算。
【详解】125×99×8
=125×8×99
=1000×99
=99000
32×25×4
=32×(25×4)
=32×100
=3200
3600÷25÷4
=3600÷(25×4)
=3600÷100
=36
5×49×20
=5×20×49
=100×49
=4900
27.(1)见详解;
(2)8000;100000
【分析】(1)淘气首先将24拆分为6和4两个数的乘积,然后将4和25相乘得到100,最后将6和100相乘得到600。这个过程中,淘气运用了乘法结合律,使得计算过程更加简便。
(2)首先将64拆分为8和8两个数的乘积,然后将8和125相乘得到1000,最后将8和1000相乘得到 8000。首先将32拆分为8和4两个数的乘积,然后将125和8相乘得到1000,再将25和4相乘得到100,最后将1000和100相乘得到100000。
【详解】(1)因为4×25=100,24=4×6, 利用乘法结合律可以得到: 24×25 =6×4×25 =6×(4×25) =6×100 =600
(2)64×125
=8×8×125
=8×(8×125)
=8×1000
=8000
125×25×32
=125×25×8×4
=(125×8)×(25×4)
=1000×100
=100000
28.1400本
【分析】用每个书架能摆的本数乘书架的个数,把56拆分成4×14,然后运用乘法交换律简便计算即可。
【详解】56×25
=4×14×25
=4×25×14
=100×14
=1400(本)
答:一共有1400本书。
【点睛】考查用乘法解决实际问题。注意计算过程可以利用运算定律进行简便运算。
29.3600元
【分析】先求出4箱图书的总本数,用36乘4,1本25元,再用所得积乘25,计算时可以根据乘法结合律,先求出25与4的积,再乘36。
【详解】36×4×25
=36×(4×25)
=36×100
=3600(元)
答:一共要3600元。
【点睛】熟练掌握乘法结合律在解决实际问题中应用。
30.12000元
【分析】每盒有12支,用12乘8,求出购买1盒这样的圆珠笔需要的钱数,再乘125,求出一共需要多少元;因为8×125=1000,可以根据乘法结合律进行简算。
【详解】12×8×125
=12×(8×125)
=12×1000
=12000(元)
答:一共需要12000元。
【点睛】本题主要考查了学生对乘法结合律的掌握与灵活运用。
31.1400户
【分析】小区总共的幢数乘每幢楼的层数等于总共的层数,再乘每层的户数即可解答。
【详解】7×25×8
=7×(25×8)
=7×200
=1400(户)
答:这个小区一共住了1400户人家。
【点睛】本题主要考查学生对乘法结合律的掌握和灵活运用。
32.180块
【分析】可以先算出每个班发多少块雪糕,列式为30×2,然后再算3个班一共需要买多少块雪糕,列式为30×2×3,据此解答。
【详解】30×2×3
=60×3
=180(块)
答:一共需要买180块雪糕。
【点睛】本题考查了学生运用连乘解决实际问题的能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
