24.3锐角三角函数暑假预习练(含解析) 华东师大版数学九年级上册
文档属性
| 名称 | 24.3锐角三角函数暑假预习练(含解析) 华东师大版数学九年级上册 | 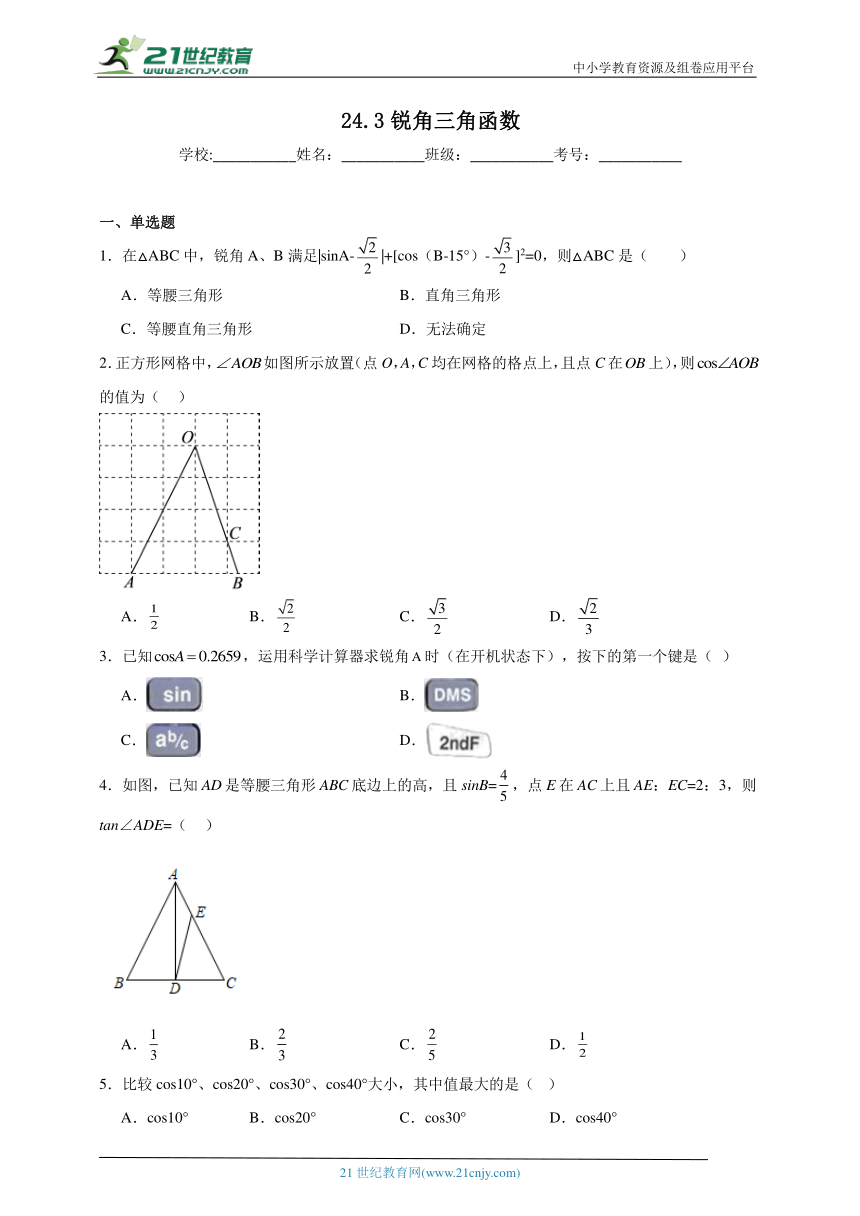 | |
| 格式 | docx | ||
| 文件大小 | 794.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 20:20:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.3锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,锐角A、B满足|sinA-|+[cos(B-15°)-]2=0,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.无法确定
2.正方形网格中,如图所示放置(点O,A,C均在网格的格点上,且点C在上),则的值为( )
A. B. C. D.
3.已知,运用科学计算器求锐角时(在开机状态下),按下的第一个键是( )
A. B.
C. D.
4.如图,已知AD是等腰三角形ABC底边上的高,且sinB=,点E在AC上且AE:EC=2:3,则tan∠ADE=( )
A. B. C. D.
5.比较cos10°、cos20°、cos30°、cos40°大小,其中值最大的是( )
A.cos10° B.cos20° C.cos30° D.cos40°
6.在Rt△ABC中,∠C=90°,若,则的值为( )
A.1 B. C. D.
7.在△ABC中,∠C=90°,sinA=,则BC∶AC等于( )
A.3∶4 B.4∶3 C.3∶5 D.4∶5
8.如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,cos∠AOB=反比例函数在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
A.15 B.20 C.30 D.40
9.已知为锐角,且,则( )
A. B. C. D.
10.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于( )
A.1 B. C. D.
11.当锐角时,则的值是( )
A. B. C. D.
12.在中,,,则的值为( )
A.1 B. C. D.
二、填空题
13.若等腰三角形的两边长分别为和,则底角的正切值为 .
14.计算: .
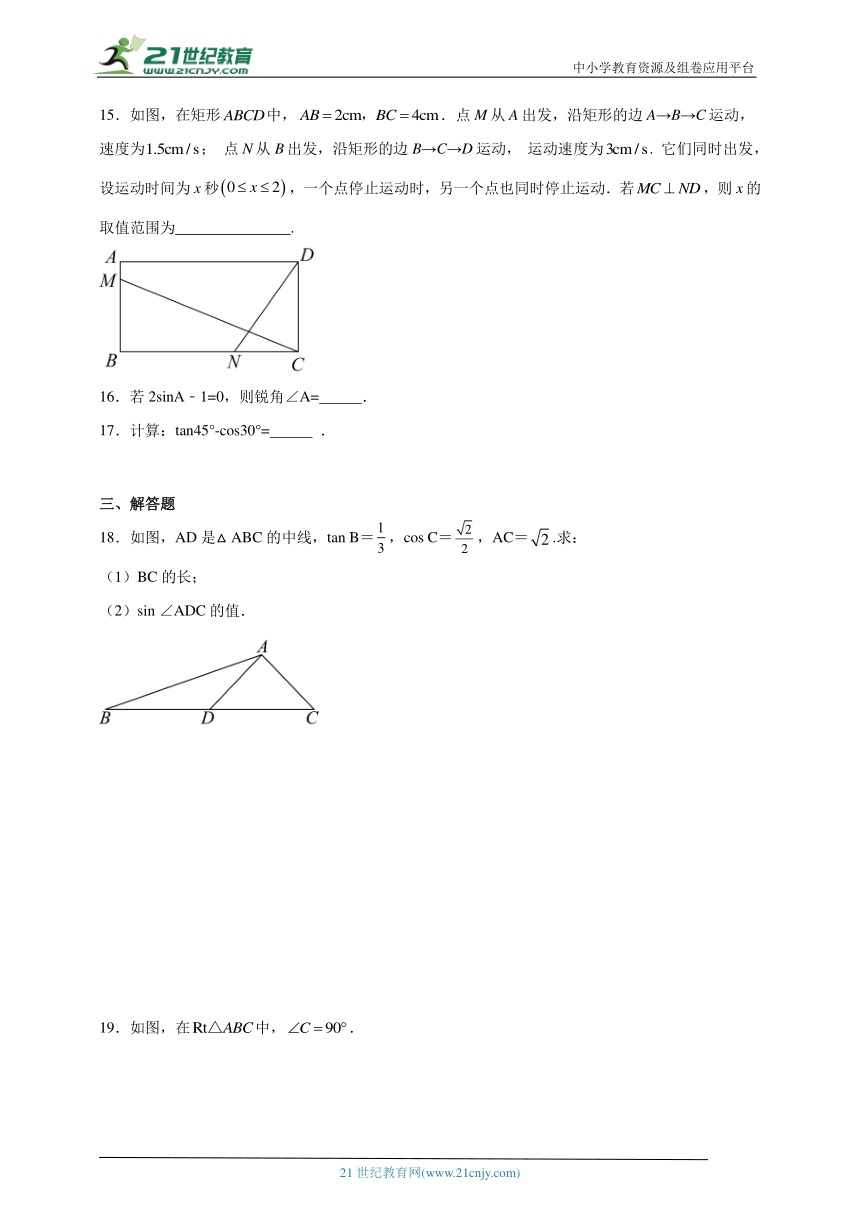
15.如图,在矩形中,.点M从A出发,沿矩形的边A→B→C运动,速度为; 点N从B出发,沿矩形的边B→C→D运动, 运动速度为. 它们同时出发,设运动时间为x秒,一个点停止运动时,另一个点也同时停止运动.若,则x的取值范围为 .
16.若2sinA﹣1=0,则锐角∠A= .
17.计算:tan45°-cos30°= .
三、解答题
18.如图,AD是△ABC的中线,tan B=,cos C=,AC=.求:
(1)BC的长;
(2)sin ∠ADC的值.
19.如图,在中,.
(1)求证:.
(2)若,求的值.
20.计算:
(1);
(2).
21.计算:(sin30°)﹣1+﹣tan45°.
22.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
23.如图,在的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,线段的端点均在格点上,仅用无刻度的直尺,按下列要求完成画图,并保留作图痕迹.
(1)在图①中画一条射线,使.
(2)在图②中画一条射线,使.
24.先化简,再求值:﹣1,其中a=2sin60°﹣tan45°,b=1.
《24.3锐角三角函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D D A B A B C B
题号 11 12
答案 A C
1.C
【分析】根据非负数的性质求出sinA和cos(B-15°)的值,然后求出∠A和∠B的度数,即可判断△ABC的形状.
【详解】∵|sinA-|+[cos(B-15°)-]2=0,
∴,且,
∴sinA=,
∴∠A=45°,
∵,
∴cos(B-15°)=,
∴∠B-15°=30°,
∴∠B=45°,
∴∠C=90°,
∴△ABC为等腰直角三角形,
故选:C.
【点睛】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
2.B
【分析】作交于点D,首先得到,然后根据勾股定理求出的长度,然后即可求出的值.
【详解】作交于点D,
由网格的特点可得,
∵,
∴.
故选:B.
【点睛】本题主要考查了求特殊角三角函数值,解题的关键在于根据题意构造直角三角形求解.
3.D
【分析】根据计算器求锐角的方法即可得结论.
【详解】∵cosA=0.2659,运用科学计算器求锐角A时(在开机状态下)的按键顺序是:2ndF,cos,0.2659,∴按下的第一个键是2ndF.
故选:D.
【点睛】本题考查了计算器﹣三角函数,解决本题的关键是熟练利用计算器.
4.D
【分析】作EF∥CD,根据设AD=4x、AC=5x,知CD=3x,再由AE:EC=2:3分别表示出DF、AF、EF的长,继而可得∠ADE的正切值.
【详解】解:如图.作EF∥CD交AD于F点.
∵,
∴设AD=4x,则AC=5x,CD=3x,
∵
∴.
∵,
∴.
∴,
故选:D.
【点睛】本题考查了解直角三角形、勾股定理、比例线段的性质等知识点,构建以∠ADE为内角的直角三角形是解题的出发点,根据已知条件表示出所需线段的长度是关键.
5.A
【分析】根据同名三角函数大小的比较方法比较即可.
【详解】∵,
∴.
故选:A.
【点睛】本题考查了同名三角函数大小的比较方法,熟记锐角的正弦、正切值随角度的增大而增大;锐角的余弦、余切值随角度的增大而减小.
6.B
【分析】根据互余角的三角函数间的关系:sin(90°-α)=cosα,cos(90°-α)=sinα解答即可.
【详解】解:解:∵在△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴sinA= cosB=,
故选:B.
【点睛】本题考查了互余两角的三角函数关系式,掌握当∠A+∠B=90°时, sinA= cosB是解题的关键.
7.A
【详解】
,设a=3x,则c=5x,
∴,
∴b=4x,
故选A.
8.B
【分析】过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,结合反比例函数图象上点的坐标特征即可求出a的值,再根据四边形OACB是菱形、点F在边BC上,即可得出,结合菱形的面积公式即可得出结论.
【详解】解:过点A作AM⊥x轴于点M,如图所示.
设OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,cos∠AOB=,
∴OM=OA cos∠AOB=a,AM==a,
∴点A的坐标为(a,a).
∵点A在反比例函数y=的图象上,
∴a×a=24,
解得:a=5,或a=-5(舍去).
∴OM=3,AM=4,OB=OA=5.
∵四边形OBCA是菱形,点F在边BC上,
∴.
故选:B.
【点睛】本题考查了菱形的性质、解直角三角形以及反比例函数图象上点的坐标特征,解题的关键是找出.
9.C
【分析】根据特殊三角函数值可直接得出答案.
【详解】已知为锐角,且,
,即.
故选C.
【点睛】本题主要考查特殊三角函数值,熟记特殊三角函数值是解题的关键.
10.B
【详解】试题解析:
由题知,
所以
故应选:B.
11.A
【分析】由30°角的正弦值直接可得答案.
【详解】解:∵sin30°=;
故选A.
【点睛】本题考查了特殊角的三角函数值,熟记特殊角的三角函数值是解题关键.
12.C
【分析】本题考查了锐角三角函数的定义,根据特殊角三角函数值,可得答案.熟练掌握锐角三角函数的正弦,余弦,正切是解题的关键.
【详解】解:由中,, ,由是锐角,得,
∴,
则,
故选:C.
13.或
【分析】已知边长6和8,故腰为6,6,8或者8,8,6两种情况讨论.
【详解】
如图,在△ABC中,AB=AC,∠B=∠C=∠α,过A作AD⊥BC于D.
(1)当AB=6,BC=8时,
则CD=4,
在Rt△ACD中,AD为.
则底角tanα==;
(2)当AB=8,BC=6时,则CD=3,
在Rt△ACD中,AD为.
则底角tanα=.
故答案为或.
【点睛】本题考查了解直角三角形,等腰三角形边的讨论是解题的关键.
14.
【分析】根据特殊角的三角函数值直接书写即可.
【详解】
故答案为:.
【点睛】本题考查了特殊角的三角函数值,牢固记忆是解题的关键.
15.
【分析】如果点M在上,点N在上,时,易证,则,求出,即,解得,当时,,则M运动到B点,N运动到C点,以后N在上运动,M在上运动,由,则,即可得出结果.
【详解】解:如果点M在上,点N在上,时,
则,
∴,则,
∴,即,
∴,
即:,
解得:,
当时,,
∴M运动到B点,N运动到C点,
以后N在上运动,M在上运动,
∵,
∴,
∵,一个点停止运动时,另一个点也同时停止运动,
∴若,x的值为:,
故答案为:.
【点睛】本题考查了矩形的性质、一元一次方程的应用、三角函数等知识;熟练掌握矩形的性质,列出一元一次方程是解题的关键.
16.30°.
【分析】直接利用特殊角的三角函数值求出答案.
【详解】解:∵2sinA﹣1=0,
∴2sinA=1,
则sinA=,
则锐角∠A=30°.
故答案为:30°.
【点评】此题主要考查了特殊角的三角函数值,正确记忆有关特殊角的三角函数值是解题关键.
17.1-
【分析】根据特殊角三角函数值代入求解即可.
【详解】解:tan45°-cos30°=1-
故答案为:1-
【点睛】本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.
18.(1)BC=4;(2)sin ∠ADC=.
【详解】(1)如图,作AE⊥BC,
∴CE=AC cosC=1,∴AE=CE=1,,
∴BE=3AE=3,∴BC=4;
(2)∵AD是△ABC的中线,∴DE=1,
∴∠ADC=45°,∴.
19.(1)见解析
(2)
【分析】本题考查锐角三角形函数的知识,解题的关键是掌握正弦,余弦的应用,勾股定理的应用,利用完全平方公式,对式子进行变形,进行解答,即可.
(1)根据正弦,余弦,勾股定理,可得,,,通过变形可得,,,再进行计算即可;
(2)根据题意,,变形可得,再根据,即可求出.
【详解】(1)解:证明如下:
∵中,,
∴,,,
∴,,
∴.
(2)解:∵,
∴,
∴,
∵,
∴,
∴.
20.(1);(2)0.
【分析】将特殊角的三角函数值代入计算即可.
【详解】解:(1);
(2).
【点睛】本题考查了特殊角的三角函数值,掌握几个特殊角的三角函数值是解答本题的关键.
21.
【详解】试题分析:把特殊角的三角函数值代入进行运算即可.
试题解析:原式
22..
【分析】易证得△AMN∽△ABC,根据相似三角形的性质得到==,设AC=3x,AB=4x,由勾股定理得:BC=x,在Rt△ABC中,根据三角函数可求cosB.
【详解】∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠A=∠A,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==,
在Rt△ABC中,cosB=.
【点评】本题考查了锐角三角函数的定义,相似三角形的判定和性质,勾股定理,本题关键是表示出BC,AB.
23.(1)见解析;(2)见解析
【分析】(1)先确定直角三角形的直角,①当∠ACB为直角时,需要保证AC=2BC;②当∠ABC为直角时,需要保证AB=2BC;
(2)∠ABD是直角,需要保证BD=即可.
【详解】解:(1)如图所示.
(2)如图所示.
【点睛】本题考查的是锐角三角函数的定义,能够找到合适的直角三角形进行转换是解题的关键.
24.
【分析】对待求式的分子、分母进行因式分解,并将除法化为乘法可得×-1,通过约分即可得到化简结果;先利用特殊角的三角函数值求出a的值,再将a、b的值代入化简结果中计算即可解答本题.
【详解】原式=×-1
=-1
=
=,
当a═2sin60°﹣tan45°=2×﹣1=﹣1,b=1时,
原式=.
【点睛】本题考查了分式的化简求值,解题的关键是熟练的掌握分式的化简求值运算法则.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.3锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在△ABC中,锐角A、B满足|sinA-|+[cos(B-15°)-]2=0,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.无法确定
2.正方形网格中,如图所示放置(点O,A,C均在网格的格点上,且点C在上),则的值为( )
A. B. C. D.
3.已知,运用科学计算器求锐角时(在开机状态下),按下的第一个键是( )
A. B.
C. D.
4.如图,已知AD是等腰三角形ABC底边上的高,且sinB=,点E在AC上且AE:EC=2:3,则tan∠ADE=( )
A. B. C. D.
5.比较cos10°、cos20°、cos30°、cos40°大小,其中值最大的是( )
A.cos10° B.cos20° C.cos30° D.cos40°
6.在Rt△ABC中,∠C=90°,若,则的值为( )
A.1 B. C. D.
7.在△ABC中,∠C=90°,sinA=,则BC∶AC等于( )
A.3∶4 B.4∶3 C.3∶5 D.4∶5
8.如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,cos∠AOB=反比例函数在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
A.15 B.20 C.30 D.40
9.已知为锐角,且,则( )
A. B. C. D.
10.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于( )
A.1 B. C. D.
11.当锐角时,则的值是( )
A. B. C. D.
12.在中,,,则的值为( )
A.1 B. C. D.
二、填空题
13.若等腰三角形的两边长分别为和,则底角的正切值为 .
14.计算: .
15.如图,在矩形中,.点M从A出发,沿矩形的边A→B→C运动,速度为; 点N从B出发,沿矩形的边B→C→D运动, 运动速度为. 它们同时出发,设运动时间为x秒,一个点停止运动时,另一个点也同时停止运动.若,则x的取值范围为 .
16.若2sinA﹣1=0,则锐角∠A= .
17.计算:tan45°-cos30°= .
三、解答题
18.如图,AD是△ABC的中线,tan B=,cos C=,AC=.求:
(1)BC的长;
(2)sin ∠ADC的值.
19.如图,在中,.
(1)求证:.
(2)若,求的值.
20.计算:
(1);
(2).
21.计算:(sin30°)﹣1+﹣tan45°.
22.如图,在Rt△ABC中,∠C=90°,M是直角边AC上一点,MN⊥AB于点N,AN=3,AM=4,求cosB的值.
23.如图,在的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1,线段的端点均在格点上,仅用无刻度的直尺,按下列要求完成画图,并保留作图痕迹.
(1)在图①中画一条射线,使.
(2)在图②中画一条射线,使.
24.先化简,再求值:﹣1,其中a=2sin60°﹣tan45°,b=1.
《24.3锐角三角函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D D A B A B C B
题号 11 12
答案 A C
1.C
【分析】根据非负数的性质求出sinA和cos(B-15°)的值,然后求出∠A和∠B的度数,即可判断△ABC的形状.
【详解】∵|sinA-|+[cos(B-15°)-]2=0,
∴,且,
∴sinA=,
∴∠A=45°,
∵,
∴cos(B-15°)=,
∴∠B-15°=30°,
∴∠B=45°,
∴∠C=90°,
∴△ABC为等腰直角三角形,
故选:C.
【点睛】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
2.B
【分析】作交于点D,首先得到,然后根据勾股定理求出的长度,然后即可求出的值.
【详解】作交于点D,
由网格的特点可得,
∵,
∴.
故选:B.
【点睛】本题主要考查了求特殊角三角函数值,解题的关键在于根据题意构造直角三角形求解.
3.D
【分析】根据计算器求锐角的方法即可得结论.
【详解】∵cosA=0.2659,运用科学计算器求锐角A时(在开机状态下)的按键顺序是:2ndF,cos,0.2659,∴按下的第一个键是2ndF.
故选:D.
【点睛】本题考查了计算器﹣三角函数,解决本题的关键是熟练利用计算器.
4.D
【分析】作EF∥CD,根据设AD=4x、AC=5x,知CD=3x,再由AE:EC=2:3分别表示出DF、AF、EF的长,继而可得∠ADE的正切值.
【详解】解:如图.作EF∥CD交AD于F点.
∵,
∴设AD=4x,则AC=5x,CD=3x,
∵
∴.
∵,
∴.
∴,
故选:D.
【点睛】本题考查了解直角三角形、勾股定理、比例线段的性质等知识点,构建以∠ADE为内角的直角三角形是解题的出发点,根据已知条件表示出所需线段的长度是关键.
5.A
【分析】根据同名三角函数大小的比较方法比较即可.
【详解】∵,
∴.
故选:A.
【点睛】本题考查了同名三角函数大小的比较方法,熟记锐角的正弦、正切值随角度的增大而增大;锐角的余弦、余切值随角度的增大而减小.
6.B
【分析】根据互余角的三角函数间的关系:sin(90°-α)=cosα,cos(90°-α)=sinα解答即可.
【详解】解:解:∵在△ABC中,∠C=90°,
∴∠A+∠B=90°,
∴sinA= cosB=,
故选:B.
【点睛】本题考查了互余两角的三角函数关系式,掌握当∠A+∠B=90°时, sinA= cosB是解题的关键.
7.A
【详解】
,设a=3x,则c=5x,
∴,
∴b=4x,
故选A.
8.B
【分析】过点A作AM⊥x轴于点M,设OA=a,通过解直角三角形找出点A的坐标,结合反比例函数图象上点的坐标特征即可求出a的值,再根据四边形OACB是菱形、点F在边BC上,即可得出,结合菱形的面积公式即可得出结论.
【详解】解:过点A作AM⊥x轴于点M,如图所示.
设OA=a,
在Rt△OAM中,∠AMO=90°,OA=a,cos∠AOB=,
∴OM=OA cos∠AOB=a,AM==a,
∴点A的坐标为(a,a).
∵点A在反比例函数y=的图象上,
∴a×a=24,
解得:a=5,或a=-5(舍去).
∴OM=3,AM=4,OB=OA=5.
∵四边形OBCA是菱形,点F在边BC上,
∴.
故选:B.
【点睛】本题考查了菱形的性质、解直角三角形以及反比例函数图象上点的坐标特征,解题的关键是找出.
9.C
【分析】根据特殊三角函数值可直接得出答案.
【详解】已知为锐角,且,
,即.
故选C.
【点睛】本题主要考查特殊三角函数值,熟记特殊三角函数值是解题的关键.
10.B
【详解】试题解析:
由题知,
所以
故应选:B.
11.A
【分析】由30°角的正弦值直接可得答案.
【详解】解:∵sin30°=;
故选A.
【点睛】本题考查了特殊角的三角函数值,熟记特殊角的三角函数值是解题关键.
12.C
【分析】本题考查了锐角三角函数的定义,根据特殊角三角函数值,可得答案.熟练掌握锐角三角函数的正弦,余弦,正切是解题的关键.
【详解】解:由中,, ,由是锐角,得,
∴,
则,
故选:C.
13.或
【分析】已知边长6和8,故腰为6,6,8或者8,8,6两种情况讨论.
【详解】
如图,在△ABC中,AB=AC,∠B=∠C=∠α,过A作AD⊥BC于D.
(1)当AB=6,BC=8时,
则CD=4,
在Rt△ACD中,AD为.
则底角tanα==;
(2)当AB=8,BC=6时,则CD=3,
在Rt△ACD中,AD为.
则底角tanα=.
故答案为或.
【点睛】本题考查了解直角三角形,等腰三角形边的讨论是解题的关键.
14.
【分析】根据特殊角的三角函数值直接书写即可.
【详解】
故答案为:.
【点睛】本题考查了特殊角的三角函数值,牢固记忆是解题的关键.
15.
【分析】如果点M在上,点N在上,时,易证,则,求出,即,解得,当时,,则M运动到B点,N运动到C点,以后N在上运动,M在上运动,由,则,即可得出结果.
【详解】解:如果点M在上,点N在上,时,
则,
∴,则,
∴,即,
∴,
即:,
解得:,
当时,,
∴M运动到B点,N运动到C点,
以后N在上运动,M在上运动,
∵,
∴,
∵,一个点停止运动时,另一个点也同时停止运动,
∴若,x的值为:,
故答案为:.
【点睛】本题考查了矩形的性质、一元一次方程的应用、三角函数等知识;熟练掌握矩形的性质,列出一元一次方程是解题的关键.
16.30°.
【分析】直接利用特殊角的三角函数值求出答案.
【详解】解:∵2sinA﹣1=0,
∴2sinA=1,
则sinA=,
则锐角∠A=30°.
故答案为:30°.
【点评】此题主要考查了特殊角的三角函数值,正确记忆有关特殊角的三角函数值是解题关键.
17.1-
【分析】根据特殊角三角函数值代入求解即可.
【详解】解:tan45°-cos30°=1-
故答案为:1-
【点睛】本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.
18.(1)BC=4;(2)sin ∠ADC=.
【详解】(1)如图,作AE⊥BC,
∴CE=AC cosC=1,∴AE=CE=1,,
∴BE=3AE=3,∴BC=4;
(2)∵AD是△ABC的中线,∴DE=1,
∴∠ADC=45°,∴.
19.(1)见解析
(2)
【分析】本题考查锐角三角形函数的知识,解题的关键是掌握正弦,余弦的应用,勾股定理的应用,利用完全平方公式,对式子进行变形,进行解答,即可.
(1)根据正弦,余弦,勾股定理,可得,,,通过变形可得,,,再进行计算即可;
(2)根据题意,,变形可得,再根据,即可求出.
【详解】(1)解:证明如下:
∵中,,
∴,,,
∴,,
∴.
(2)解:∵,
∴,
∴,
∵,
∴,
∴.
20.(1);(2)0.
【分析】将特殊角的三角函数值代入计算即可.
【详解】解:(1);
(2).
【点睛】本题考查了特殊角的三角函数值,掌握几个特殊角的三角函数值是解答本题的关键.
21.
【详解】试题分析:把特殊角的三角函数值代入进行运算即可.
试题解析:原式
22..
【分析】易证得△AMN∽△ABC,根据相似三角形的性质得到==,设AC=3x,AB=4x,由勾股定理得:BC=x,在Rt△ABC中,根据三角函数可求cosB.
【详解】∵∠C=90°,MN⊥AB,
∴∠C=∠ANM=90°,
又∵∠A=∠A,
∴△AMN∽△ABC,
∴==,
设AC=3x,AB=4x,
由勾股定理得:BC==,
在Rt△ABC中,cosB=.
【点评】本题考查了锐角三角函数的定义,相似三角形的判定和性质,勾股定理,本题关键是表示出BC,AB.
23.(1)见解析;(2)见解析
【分析】(1)先确定直角三角形的直角,①当∠ACB为直角时,需要保证AC=2BC;②当∠ABC为直角时,需要保证AB=2BC;
(2)∠ABD是直角,需要保证BD=即可.
【详解】解:(1)如图所示.
(2)如图所示.
【点睛】本题考查的是锐角三角函数的定义,能够找到合适的直角三角形进行转换是解题的关键.
24.
【分析】对待求式的分子、分母进行因式分解,并将除法化为乘法可得×-1,通过约分即可得到化简结果;先利用特殊角的三角函数值求出a的值,再将a、b的值代入化简结果中计算即可解答本题.
【详解】原式=×-1
=-1
=
=,
当a═2sin60°﹣tan45°=2×﹣1=﹣1,b=1时,
原式=.
【点睛】本题考查了分式的化简求值,解题的关键是熟练的掌握分式的化简求值运算法则.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
