24.4解直角三角形暑假预习练(含解析) 华东师大版数学九年级上册
文档属性
| 名称 | 24.4解直角三角形暑假预习练(含解析) 华东师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 20:21:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知直角三角形ABC中,斜边AB的长为m,∠B=40°,则直角边BC的长是( )
A.m·sin40° B.m·cos40° C.m·tan40° D.
2.某水坝的坡度 i =1∶,坡长AB=20 m,则坝的高度为( )
A.10 m B.20 m C.40 m D.2m
3.如图所示,一架飞机在空中A点处测得飞行高度为h米,从飞机上看到地面指挥站B的俯角为α,则飞机与地面指挥站间的水平距离为( )
A.h·sinα米 B.h·cosα米 C.h·tanα米 D.米
4.如图,为测量建筑物CD的高度,在A点测得建筑物顶部D点的仰角为45°,再向建筑物CD前进30米到达B点,测得建筑物顶部D点的仰角为60°(A,B,C三点在一条直线上),则建筑物CD的高度为( )
A. B. C. D.
5.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米 B.10米 C.10米 D.20米
6.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A. B. C. D.
7.在下列情况下,可解的直角三角形是( )
A.已知b=3,∠C=90° B.已知∠C=90°,∠B=46°
C.已知a=3,b=6,∠C=90° D.已知∠B=15°,∠A=65°
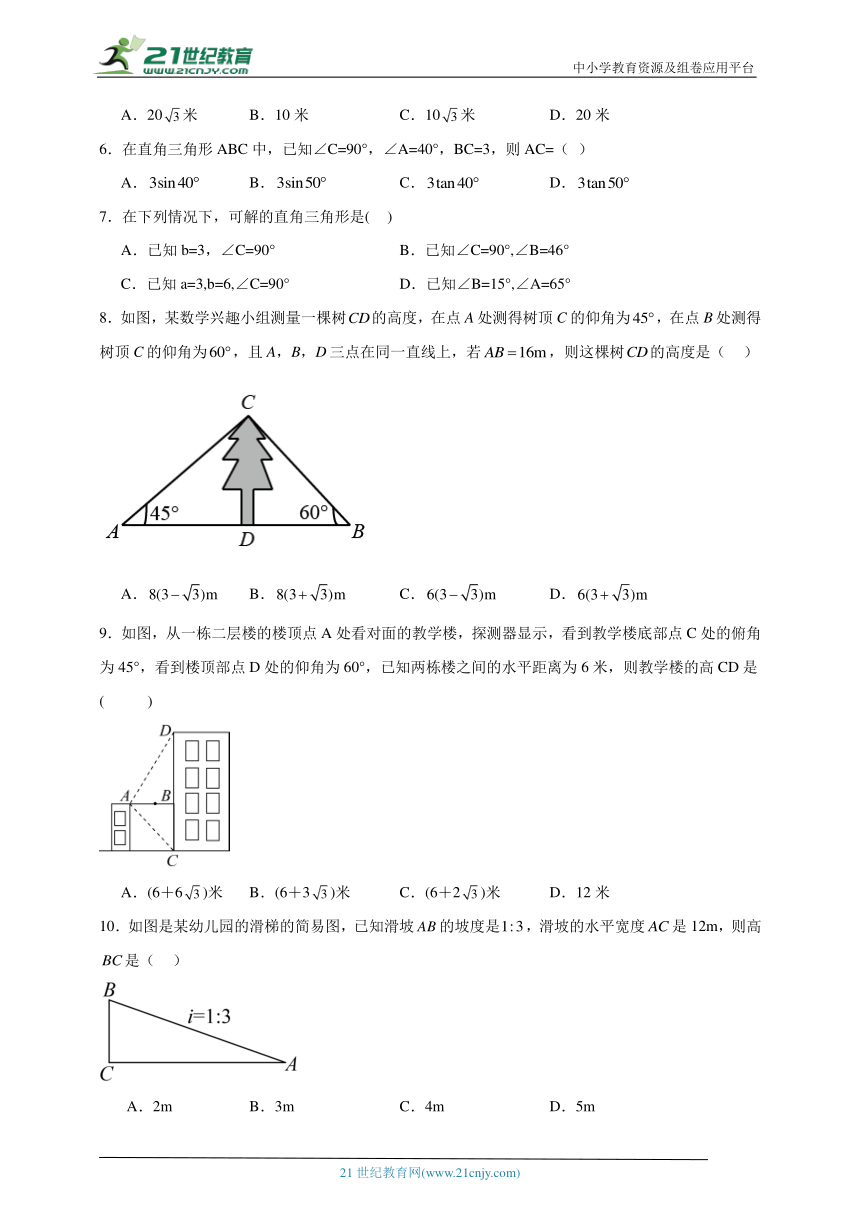
8.如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为,在点B处测得树顶C的仰角为,且A,B,D三点在同一直线上,若,则这棵树的高度是( )
A. B. C. D.
9.如图,从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是( )
A.(6+6)米 B.(6+3)米 C.(6+2)米 D.12米
10.如图是某幼儿园的滑梯的简易图,已知滑坡的坡度是,滑坡的水平宽度是12m,则高是( )
A.2m B.3m C.4m D.5m
11.如图,在高米,坡角为的楼梯表面铺地毯,地毯的长至少需( )
A.米 B.米 C.米 D.无法确定
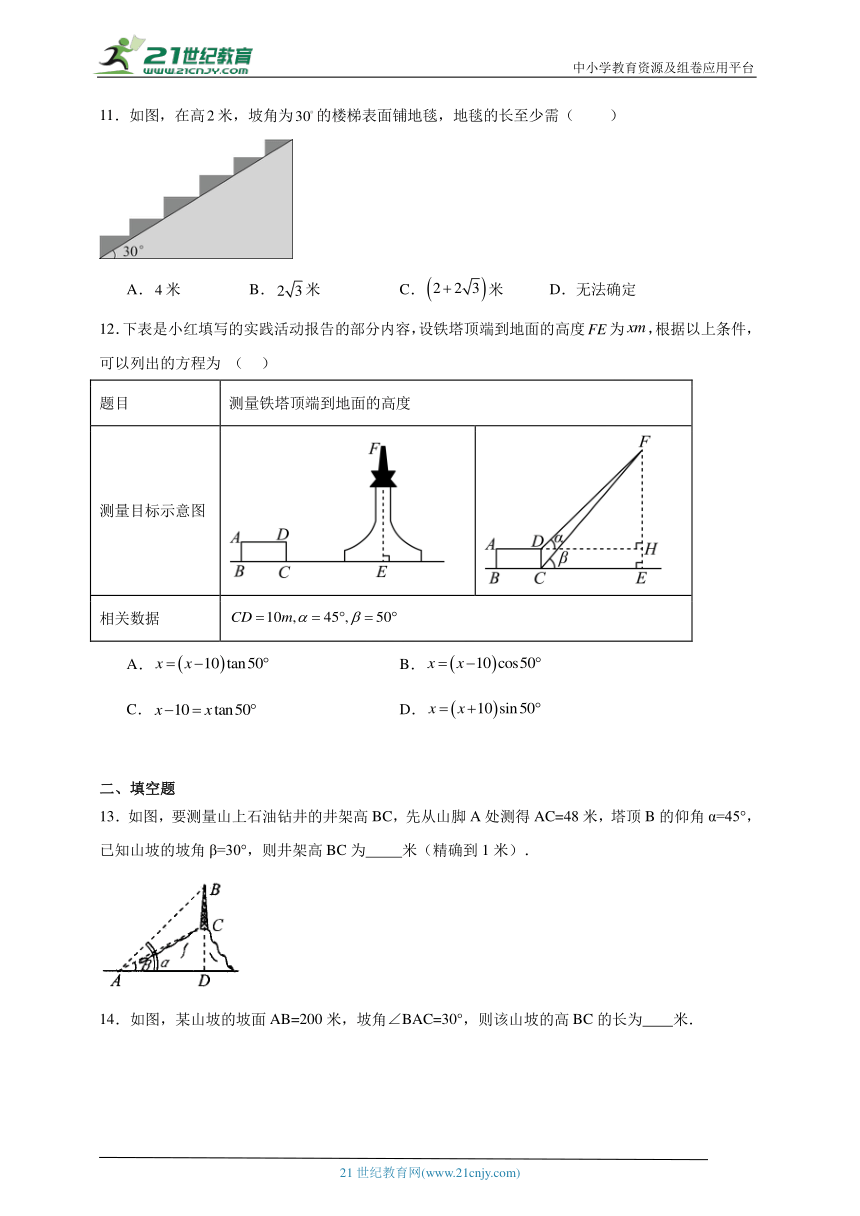
12.下表是小红填写的实践活动报告的部分内容,设铁塔顶端到地面的高度为,根据以上条件,可以列出的方程为 ( )
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据
A. B.
C. D.
二、填空题
13.如图,要测量山上石油钻井的井架高BC,先从山脚A处测得AC=48米,塔顶B的仰角α=45°,已知山坡的坡角β=30°,则井架高BC为 米(精确到1米).
14.如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为 米.
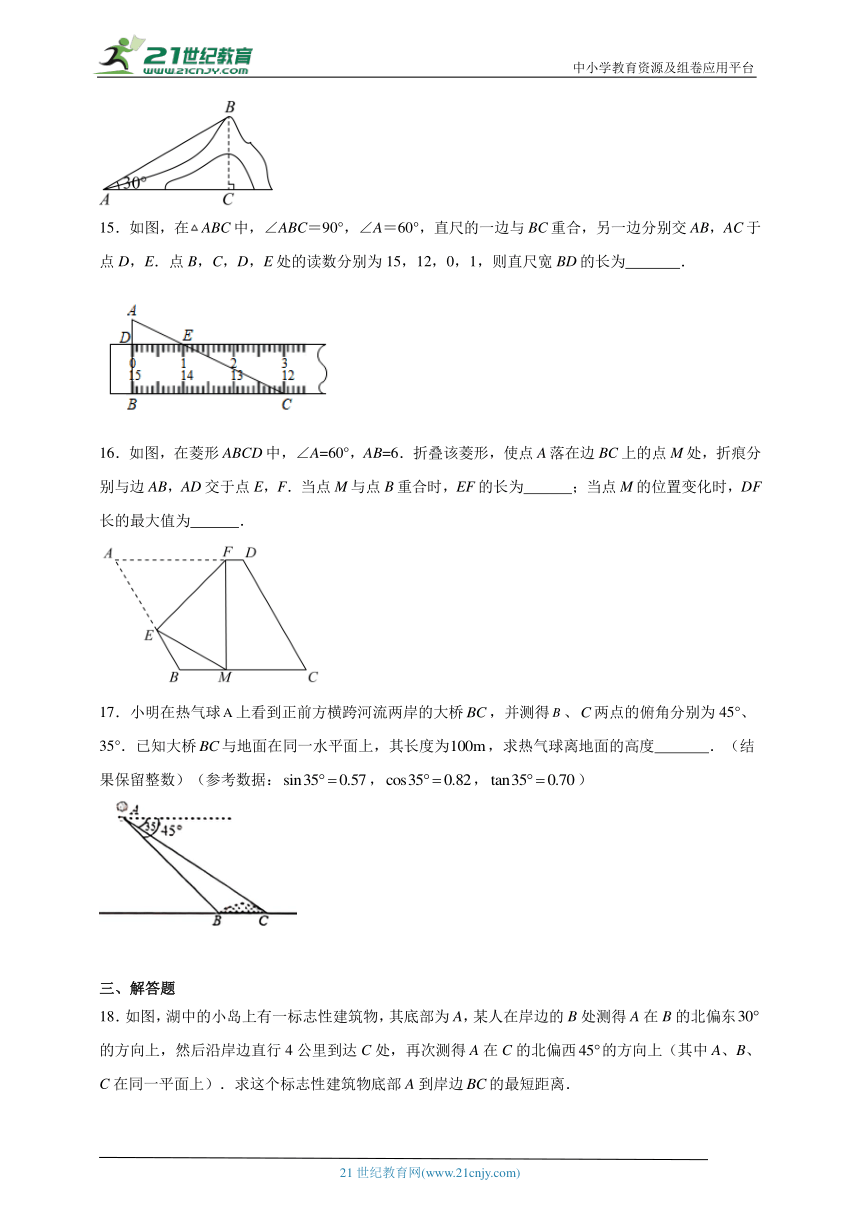
15.如图,在ABC中,∠ABC=90°,∠A=60°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺宽BD的长为 .
16.如图,在菱形ABCD中,∠A=60°,AB=6.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M与点B重合时,EF的长为 ;当点M的位置变化时,DF长的最大值为 .
17.小明在热气球上看到正前方横跨河流两岸的大桥,并测得、两点的俯角分别为45°、35°.已知大桥与地面在同一水平面上,其长度为,求热气球离地面的高度 .(结果保留整数)(参考数据:,,)
三、解答题
18.如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边的最短距离.
19.已知:△ABC中,∠C=90°.
(1)a=6,b=2,求∠A,∠B,c;
(2)a=24,c=24,求∠A,∠B,b.
20.如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=18°,∠ACD=14°.求电子警察安装在悬臂灯杆上的高度AD的长.
(参考数据:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
21.在等腰△ABC中,AC=BC,是直角三角形,∠DAE=90°,∠ADE=∠ACB,连接BD,BE,点F是BD的中点,连接CF.
(1)当∠CAB=45°时.
①如图1,当顶点D在边AC上时,请直接写出∠EAB与∠CBA的数量关系是 .线段BE与线段CF的数量关系是 ;
②如图2,当顶点D在边AB上时,(1)中线段BE与线段CF的数量关系是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
学生经过讨论,探究出以下解决问题的思路,仅供大家参考:
思路一:作等腰△ABC底边上的高CM,并取BE的中点N,再利用三角形全等或相似有关知识来解决问题;
思路二:取DE的中点G,连接AG,CG,并把绕点C逆时针旋转90°,再利用旋转性质、三角形全等或相似有关知识来解快问题.
(2)当∠CAB=30°时,如图3,当顶点D在边AC上时,写出线段BE与线段CF的数量关系,并说明理由.
22.如图,在△ABC中,∠ABC=90°,∠A=30°,D是边AB上一点,∠BDC=45°,AD=4,求BC的长.(结果保留根号)
23.某校教室A位于一地O的正西方向,OA=200米,一部拖拉机从O出发,以5米/秒的速度沿北偏西60°方向行驶,设拖拉机噪音污染半径为125米,试问:教室A是否在噪音污染范围内?若不在,说明理由,若在,求教室A受污染的时间.
24.如图所示,一堤坝的坡角,坡面长度米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角,则此时应将坝底向外拓宽多少米?(结果保留到 米)(参考数据:,,)
《24.4解直角三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D B C D C A A C
题号 11 12
答案 C A
1.B
【详解】根据∠B的余弦的定义得,cosB=,所以BC=ABcosB,即BC=mcos40°,
故选B.
2.A
【详解】如图,因为tanA=,又tanA=,所以=,设BC=x,则AC=x,由勾股定理得,AC2+BC2=AB2,即(x)2+x2=202,解得x=10,故选A.
3.D
【分析】由锐角三角函数的定义直接进行解答即可.
【详解】解:如图所示,
∵AC=h,∠ABC=α,
∴BC= 米.
故选D.
【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,根据题意画出图形,利用数形结合求解是解答此题的关键.
4.B
【分析】分别在与中表示出与的长,由建立等量关系,列方程求解.
【详解】解:在中,;
在中,.
,
解得.
故选:B.
【点睛】本题考查了三角函数的简单应用,根据题目所给信息列出等量关系是解题的关键.
5.C
【分析】首先证明BD=AD=20米,解直角三角形求出BC即可.
【详解】解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD sin60°=10(米),
故选:C.
【点睛】本题考查解直角三角形的应用,等腰三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.D
【详解】试题分析:∵∠C=90°,∠A=40°,∴∠B=50°.
∵BC=3,,∴.
故选D.
考点:1.直角三角形两锐角的关系;2.锐角三角函数定义.
7.C
【分析】要解直角三角形,必须求出直角三角形的三个内角和三边长.
【详解】A项中,缺少∠A或∠B的值,故不能解直角三角形;
B项中,知道角的关系,但是没有边的大小,故不能解直角三角形;
C项中,利用勾股定理求出c的值,然后利用锐角三角函数的定义求出∠A和∠B.
D项中,∠C=100°,不是直角三角形.
故选C.
【点睛】本题考查解直角三角形的应用,解题的关键是掌握直角三角形的性质.
8.A
【分析】设CD=x,在Rt△ADC中,∠A=45°,可得CD=AD=x,BD=16-x,在Rt△BCD中,用∠B的正切函数值即可求解.
【详解】设CD=x,在Rt△ADC中,∠A=45°,
∴CD=AD=x,
∴BD=16-x,
在Rt△BCD中,∠B=60°,
∴,
即:,
解得,
故选A.
【点睛】本题考查三角函数,根据直角三角形的边的关系,建立三角函数模型是解题的关键.
9.A
【分析】在Rt△ABC求出CB,在Rt△ABD中求出BD,继而可求出CD.
【详解】解:在Rt△ACB中,∠CAB=45°,AB⊥DC,AB=6米,
∴BC=6米,
在Rt△ABD中,
∵tan∠BAD=,
∴BD=AB tan∠BAD=6米,
∴DC=CB+BD=6+6(米).
故选:A.
【点睛】本题考查解直角三角形的应用-仰角俯角问题,熟练掌握三角函数的定义是解题关键.
10.C
【分析】本题考查了解直角三角形的应用 坡度坡角问题,解题的关键是根据题意得,代入即可求解.
【详解】解:∵滑坡的坡度是,
∴在中,,
∵,
∴,
故选:C.
11.C
【分析】地毯水平的部分的和是水平边的和,竖直的部分的和是竖直边,因此根据勾股定理求出直角三角形两直角边即可.
【详解】解:已知直角三角形的高是米,根据三角函数得到:水平的直角边是,
则地毯水平的部分的和是水平边的和,竖直的部分的和是竖直边,
则地毯的长是米.
故选.
【点睛】本题考查了勾股定理的知识,与实际生活相联系,加深了学生学习数学的积极性.
12.A
【分析】过D作DH⊥EF于H,则四边形DCEH是矩形,根据矩形的性质得到HE=CD=10,CE=DH,求得FH=x 10,得到CE=x 10,根据三角函数的定义列方程即可得到结论.
【详解】过D作DH⊥EF于H,
则四边形DCEH是矩形,
∴HE=CD=10,CE=DH,
∴FH=x 10,
∵∠FDH=α=45°,
∴DH=FH=x 10,
∴CE=x 10,
∵tanβ=tan50°==,
∴x=(x 10)tan 50°,
故选:A.
【点睛】本题考查了解直角三角形的应用,由实际问题抽象出边角关系的等式,正确的识别图形是解题的关键.
13.18
【分析】由已知得∠β=30,∠BDA=90°,AC=48解Rt△CDA求出AD,DC
此时在△ADB中可求出BD的长,观察图形可知BC=BD-CD.
【详解】∵ ∠CDA=90° AC=48 β=30°
∴ CD=sinα×AC=24 (三角函数定义)
AD=cosα×AC=24× (三角函数定义)
∵ ∠BDA=90° ,∠α=45°
∴ tanα==1 (三角函数定义)
∴ BD=24×
∴ BC=24× 24≈18
即井架高BC为18米.
【点睛】本题考查解直角三角形的应用,解题的关键是根据特殊角度的三角函数的知识分别得出AD、DC和BD的长.
14.100.
【详解】由题意得,∠BCA=90°,∠BAC=30°,AB=200米,
∴BC=AB=100米.
15.
【分析】先求解 再利用线段的和差可得答案.
【详解】解:由题意可得:
同理:
故答案为:
【点睛】本题考查的是锐角的正切的应用,二次根式的减法运算,掌握“利用锐角的正切求解三角形的边长”是解本题的关键.
16.
【分析】当点M与点B重合时,EF垂直平分AB,利用三角函数即可求得EF的长;根据折叠的性质可知,AF=FM,若DF取最大值,则FM取最小值,即为边AD与BC的距离DG,即可求解.
【详解】解:当点M与点B重合时,由折叠的性质知EF垂直平分AB,
∴AE=EB=AB=3,
在Rt△AEF中,∠A=60°,AE=3,
tan60°=,
∴EF=3;
当AF长取得最小值时,DF长取得最大值,
由折叠的性质知EF垂直平分AM,则AF=FM,
∴FM⊥BC时,FM长取得最小值,此时DF长取得最大值,
过点D作DG⊥BC于点C,则四边形DGMF为矩形,
∴FM=DG,
在Rt△DGC中,∠C=∠A=60°,DC=AB=6,
∴DG=DCsin60°=3,
∴DF长的最大值为AD-AF=AD-FM=AD-DG=6-3,
故答案为:3;6-3.
【点睛】本题考查了菱形的性质,折叠的性质,解直角三角形,解题的关键是灵活运用所学知识解决问题.
17.233m
【分析】作AD⊥BC交CB的延长线于D,设AD为x,表示出DB和DC,根据正切的概念求出x的值即可.
【详解】解:作AD⊥BC交CB的延长线于D,设AD为x,
由题意得,∠ABD=45°,∠ACD=35°,
在Rt△ADB中,∠ABD=45°,
∴DB=x,
在Rt△ADC中,∠ACD=35°,
,
,
解得,x≈233.
所以,热气球离地面的高度约为233米.
故答案为:233.
【点睛】本题考查的是解直角三角形的应用,理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键,解答时,注意正确作出辅助线构造直角三角形.
18.这个标志性建筑物底部A到岸边的最短距离为公里.
【分析】题目主要考查解直角三角形的应用及垂线的性质,根据题意,作出辅助线,熟练掌握运用解三角形是解题关键.
要求这个标志性建筑物底部A到岸边的最短距离也就是要求出点A到直线的最短距离,过点A作于D,然后利用所给条件求出的长即可.
【详解】解:过A作于D,则的长度就是A到岸边的最短距离.
在中,,设,则,
在中,,
由,即,
所以,
又,即,
所以,
解得.
答:这个标志性建筑物底部A到岸边的最短距离为公里.
19.(1)∠A=60°,∠B=30°,c=4;(2) b=24,∠A=∠B=45°.
【详解】试题分析:
(1)由tanA=,可得∠A=30°,从而可得∠B=60°,再由c=2b可得c=;
(2)由勾股定理可得:b=24,由tanA=可得∠A=45°,从而可得∠B=45°.
试题解析:
(1)∵在Rt△ ABC中,tanA=,
∴tanA==,
∴∠A=60°,∠B=90°-60°=30°,
∴c=2b=2×2=4;
(2)∵在Rt△ABC中,根据勾股定理有b2=c2-a2,
∴b=24,
∴ tanA==1,
∴∠A=∠B=45°.
20.AD的长为6.5 m.
【分析】设电子警察安装在悬臂灯杆上的高度AD的长为xm.通过解Rt△ADB和Rt△ACD求得BD、CD的长度,然后结合BC=CD﹣BD列出方程,并解答.
【详解】设电子警察安装在悬臂灯杆上的高度AD的长为x m.
在Rt△ADB中,tan∠ABD= ,
∴BD=,
在Rt△ACD中,tan∠ACD= ,
∴CD=,
∵BC=CD﹣BD,
∴﹣=6,
∴4x﹣x=6.
解这个方程,得x=6.5.
答:电子警察安装在悬臂灯杆上的高度AD的长为6.5 m.
【点睛】本题考查的是解直角三角形的应﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
21.(1)①,;②仍然成立,证明见解析;(2),理由见解析.
【分析】(1)①如图1中,连接BE,设DE交AB于T.首先证明再利用直角三角形斜边中线的性质解决问题即可.②解法一:如图2﹣1中,取AB的中点M,BE的中点N,连接CM,MN.证明(SAS),可得结论.解法二:如图2﹣2中,取DE的中点G,连接AG,CG,并把绕点C逆时针旋转90°得到,连接DT,GT,BG.证明四边形BEGT是平行四边形,四边形DGBT是平行四边形,可得结论.
(2)结论:BE=.如图3中,取AB的中点T,连接CT,FT.证明,可得结论.
【详解】解:(1)①如图1中,连接BE,设DE交AB于T.
∵CA=CB,∠CAB=45°,
∴∠CAB=∠ABC=45°,
∴∠ACB=90°,
∵∠ADE=∠ACB=45°,∠DAE=90°,
∴∠ADE=∠AED=45°,
∴AD=AE,
∴AT⊥DE,DT=ET,
∴AB垂直平分DE,
∴BD=BE,
∵∠BCD=90°,DF=FB,
∴CF=BD,
∴CF=BE.
故答案为:∠EAB=∠ABC,CF=BE.
②结论不变.
解法一:如图2﹣1中,取AB的中点M,BE的中点N,连接CM,MN.
∵∠ACB=90°,CA=CB,AM=BM,
∴CM⊥AB,CM=BM=AM,
由①得:
设AD=AE=y.FM=x,DM=a,
点F是BD的中点,
则DF=FB=a+x,
∵AM=BM,
∴y+a=a+2x,
∴y=2x,即AD=2FM,
∵AM=BM,EN=BN,
∴AE=2MN,MN∥AE,
∴MN=FM,∠BMN=∠EAB=90°,
∴∠CMF=∠BMN=90°,
∴(SAS),
∴CF=BN,
∵BE=2BN,
∴CF=BE.
解法二:如图2﹣2中,取DE的中点G,连接AG,CG,并把△CAG绕点C逆时针旋转90°得到,连接DT,GT,BG.
∵AD=AE,∠EAD=90°,EG=DG,
∴AG⊥DE,∠EAG=∠DAG=45°,AG=DG=EG,
∵∠CAB=45°,
∴∠CAG=90°,
∴AC⊥AG,
∴AC∥DE,
∵∠ACB=∠CBT=90°,
∴AC∥BT∥,
∵AG=BT,
∴DG=BT=EG,
∴四边形BEGT是平行四边形,四边形DGBT是平行四边形,
∴BD与GT互相平分,
∵点F是BD的中点,
∴BD与GT交于点F,
∴GF=FT,
由旋转可得;
是等腰直角三角形,
∴CF=FG=FT,
∴CF=BE.
(2)结论:BE=.
理由:如图3中,取AB的中点T,连接CT,FT.
∵CA=CB,
∴∠CAB=∠CBA=30°,∠ACB=120°,
∵AT=TB,
∴CT⊥AB,
∴AT=,
∴AB=,
∵DF=FB,AT=TB,
∴TF∥AD,AD=2FT,
∴∠FTB=∠CAB=30°,
∵∠CTB=∠DAE=90°,
∴∠CTF=∠BAE=60°,
∵∠ADE=∠ACB=60°,
∴AE=AD=FT,
∴,
∴,
∴,
∴.
【点睛】本题属于相似形综合题,考查了等腰三角形的性质,全等三角形的判定和性质,平行四边形的判定和性质,相似三角形的判定和性质,锐角三角函数的应用,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.
22.BC=2(+1).
【详解】试题分析:由题意可得△BCD为等腰直角三角形,从而BD=BC,在Rt△ABC中,由∠A的正切值可求出BC的长.
试题解析:∵∠B=90°,∠BDC=45°,
∴△BCD为等腰直角三角形,
∴BD=BC,
在Rt△ABC中,tanA=tan30°=,即,
解得:BC=2(+1).
考点: 解直角三角形
23.受到污染;30s
【分析】问教室A是否在拖拉机的噪声污染范围内,其实就是问A到OM的距离是否大于污染半径125m,如果大于则不受影响,反之则受影响.如果过A作AB⊥OM于B,那么AB就是所求的线段.直角三角形AOB中,∠AOB的度数容易求得,又已知了OA的值,那么AB便可求出了.然后进行判断即可.
如果设拖拉机从C到D教室受影响,那么要求教室受影响的时间,其实就是求CD的值,直角三角形ABC中,AB的值已经求得.又有AC的值,那么BC的值就能求出了.CD也就能求出了,然后根据时间=路程÷速度即可得出时间是多少.
【详解】解:如图,过点A作AB⊥OM于点B,
∵∠MON=60°,
∴∠AOM=90°-60°=30°.
在Rt△ABO中,∠ABO=90°,
∵sin∠AOB=,
∴AB=AO sin∠AOB=200×sin30°=100(m).
∵100m<125m.
∴教室A在拖拉机的噪声污染范围内.
根据题意,在OM上取C,D两点,连接AC,AD,使AC=AD=125m,
∵AB⊥OM,
∴B为CD的中点,即BC=DB,
∴BC===75(m),
∴CD=2BC=150(m).
即影响的时间为=30s.
【点睛】本题主要考查了解直角三角形的知识,解题的关键是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.
24.米
【分析】本题考查了解直角三角形的应用—坡度坡角问题.解题的关键是正确作出辅助线,构造直角三角形求解.
过A点作于E.在中,根据三角函数可得,,在中,根据三角函数可得,再根据即可求解.
【详解】解:过A点作于E.
在中,.
∴米,米,
在中,,
∴米,
∴米.
故此时应将坝底向外拓宽大约米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
24.4解直角三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知直角三角形ABC中,斜边AB的长为m,∠B=40°,则直角边BC的长是( )
A.m·sin40° B.m·cos40° C.m·tan40° D.
2.某水坝的坡度 i =1∶,坡长AB=20 m,则坝的高度为( )
A.10 m B.20 m C.40 m D.2m
3.如图所示,一架飞机在空中A点处测得飞行高度为h米,从飞机上看到地面指挥站B的俯角为α,则飞机与地面指挥站间的水平距离为( )
A.h·sinα米 B.h·cosα米 C.h·tanα米 D.米
4.如图,为测量建筑物CD的高度,在A点测得建筑物顶部D点的仰角为45°,再向建筑物CD前进30米到达B点,测得建筑物顶部D点的仰角为60°(A,B,C三点在一条直线上),则建筑物CD的高度为( )
A. B. C. D.
5.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米 B.10米 C.10米 D.20米
6.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A. B. C. D.
7.在下列情况下,可解的直角三角形是( )
A.已知b=3,∠C=90° B.已知∠C=90°,∠B=46°
C.已知a=3,b=6,∠C=90° D.已知∠B=15°,∠A=65°
8.如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为,在点B处测得树顶C的仰角为,且A,B,D三点在同一直线上,若,则这棵树的高度是( )
A. B. C. D.
9.如图,从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是( )
A.(6+6)米 B.(6+3)米 C.(6+2)米 D.12米
10.如图是某幼儿园的滑梯的简易图,已知滑坡的坡度是,滑坡的水平宽度是12m,则高是( )
A.2m B.3m C.4m D.5m
11.如图,在高米,坡角为的楼梯表面铺地毯,地毯的长至少需( )
A.米 B.米 C.米 D.无法确定
12.下表是小红填写的实践活动报告的部分内容,设铁塔顶端到地面的高度为,根据以上条件,可以列出的方程为 ( )
题目 测量铁塔顶端到地面的高度
测量目标示意图
相关数据
A. B.
C. D.
二、填空题
13.如图,要测量山上石油钻井的井架高BC,先从山脚A处测得AC=48米,塔顶B的仰角α=45°,已知山坡的坡角β=30°,则井架高BC为 米(精确到1米).
14.如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为 米.
15.如图,在ABC中,∠ABC=90°,∠A=60°,直尺的一边与BC重合,另一边分别交AB,AC于点D,E.点B,C,D,E处的读数分别为15,12,0,1,则直尺宽BD的长为 .
16.如图,在菱形ABCD中,∠A=60°,AB=6.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M与点B重合时,EF的长为 ;当点M的位置变化时,DF长的最大值为 .
17.小明在热气球上看到正前方横跨河流两岸的大桥,并测得、两点的俯角分别为45°、35°.已知大桥与地面在同一水平面上,其长度为,求热气球离地面的高度 .(结果保留整数)(参考数据:,,)
三、解答题
18.如图,湖中的小岛上有一标志性建筑物,其底部为A,某人在岸边的B处测得A在B的北偏东的方向上,然后沿岸边直行4公里到达C处,再次测得A在C的北偏西的方向上(其中A、B、C在同一平面上).求这个标志性建筑物底部A到岸边的最短距离.
19.已知:△ABC中,∠C=90°.
(1)a=6,b=2,求∠A,∠B,c;
(2)a=24,c=24,求∠A,∠B,b.
20.如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=18°,∠ACD=14°.求电子警察安装在悬臂灯杆上的高度AD的长.
(参考数据:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
21.在等腰△ABC中,AC=BC,是直角三角形,∠DAE=90°,∠ADE=∠ACB,连接BD,BE,点F是BD的中点,连接CF.
(1)当∠CAB=45°时.
①如图1,当顶点D在边AC上时,请直接写出∠EAB与∠CBA的数量关系是 .线段BE与线段CF的数量关系是 ;
②如图2,当顶点D在边AB上时,(1)中线段BE与线段CF的数量关系是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
学生经过讨论,探究出以下解决问题的思路,仅供大家参考:
思路一:作等腰△ABC底边上的高CM,并取BE的中点N,再利用三角形全等或相似有关知识来解决问题;
思路二:取DE的中点G,连接AG,CG,并把绕点C逆时针旋转90°,再利用旋转性质、三角形全等或相似有关知识来解快问题.
(2)当∠CAB=30°时,如图3,当顶点D在边AC上时,写出线段BE与线段CF的数量关系,并说明理由.
22.如图,在△ABC中,∠ABC=90°,∠A=30°,D是边AB上一点,∠BDC=45°,AD=4,求BC的长.(结果保留根号)
23.某校教室A位于一地O的正西方向,OA=200米,一部拖拉机从O出发,以5米/秒的速度沿北偏西60°方向行驶,设拖拉机噪音污染半径为125米,试问:教室A是否在噪音污染范围内?若不在,说明理由,若在,求教室A受污染的时间.
24.如图所示,一堤坝的坡角,坡面长度米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角,则此时应将坝底向外拓宽多少米?(结果保留到 米)(参考数据:,,)
《24.4解直角三角形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D B C D C A A C
题号 11 12
答案 C A
1.B
【详解】根据∠B的余弦的定义得,cosB=,所以BC=ABcosB,即BC=mcos40°,
故选B.
2.A
【详解】如图,因为tanA=,又tanA=,所以=,设BC=x,则AC=x,由勾股定理得,AC2+BC2=AB2,即(x)2+x2=202,解得x=10,故选A.
3.D
【分析】由锐角三角函数的定义直接进行解答即可.
【详解】解:如图所示,
∵AC=h,∠ABC=α,
∴BC= 米.
故选D.
【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,根据题意画出图形,利用数形结合求解是解答此题的关键.
4.B
【分析】分别在与中表示出与的长,由建立等量关系,列方程求解.
【详解】解:在中,;
在中,.
,
解得.
故选:B.
【点睛】本题考查了三角函数的简单应用,根据题目所给信息列出等量关系是解题的关键.
5.C
【分析】首先证明BD=AD=20米,解直角三角形求出BC即可.
【详解】解:∵∠BDC=∠A+∠ABD,∠A=30°,∠BDC=60°,
∴∠ABD=60°30°=30°,
∴∠A=∠ABD,
∴BD=AD=20米,
∴BC=BD sin60°=10(米),
故选:C.
【点睛】本题考查解直角三角形的应用,等腰三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
6.D
【详解】试题分析:∵∠C=90°,∠A=40°,∴∠B=50°.
∵BC=3,,∴.
故选D.
考点:1.直角三角形两锐角的关系;2.锐角三角函数定义.
7.C
【分析】要解直角三角形,必须求出直角三角形的三个内角和三边长.
【详解】A项中,缺少∠A或∠B的值,故不能解直角三角形;
B项中,知道角的关系,但是没有边的大小,故不能解直角三角形;
C项中,利用勾股定理求出c的值,然后利用锐角三角函数的定义求出∠A和∠B.
D项中,∠C=100°,不是直角三角形.
故选C.
【点睛】本题考查解直角三角形的应用,解题的关键是掌握直角三角形的性质.
8.A
【分析】设CD=x,在Rt△ADC中,∠A=45°,可得CD=AD=x,BD=16-x,在Rt△BCD中,用∠B的正切函数值即可求解.
【详解】设CD=x,在Rt△ADC中,∠A=45°,
∴CD=AD=x,
∴BD=16-x,
在Rt△BCD中,∠B=60°,
∴,
即:,
解得,
故选A.
【点睛】本题考查三角函数,根据直角三角形的边的关系,建立三角函数模型是解题的关键.
9.A
【分析】在Rt△ABC求出CB,在Rt△ABD中求出BD,继而可求出CD.
【详解】解:在Rt△ACB中,∠CAB=45°,AB⊥DC,AB=6米,
∴BC=6米,
在Rt△ABD中,
∵tan∠BAD=,
∴BD=AB tan∠BAD=6米,
∴DC=CB+BD=6+6(米).
故选:A.
【点睛】本题考查解直角三角形的应用-仰角俯角问题,熟练掌握三角函数的定义是解题关键.
10.C
【分析】本题考查了解直角三角形的应用 坡度坡角问题,解题的关键是根据题意得,代入即可求解.
【详解】解:∵滑坡的坡度是,
∴在中,,
∵,
∴,
故选:C.
11.C
【分析】地毯水平的部分的和是水平边的和,竖直的部分的和是竖直边,因此根据勾股定理求出直角三角形两直角边即可.
【详解】解:已知直角三角形的高是米,根据三角函数得到:水平的直角边是,
则地毯水平的部分的和是水平边的和,竖直的部分的和是竖直边,
则地毯的长是米.
故选.
【点睛】本题考查了勾股定理的知识,与实际生活相联系,加深了学生学习数学的积极性.
12.A
【分析】过D作DH⊥EF于H,则四边形DCEH是矩形,根据矩形的性质得到HE=CD=10,CE=DH,求得FH=x 10,得到CE=x 10,根据三角函数的定义列方程即可得到结论.
【详解】过D作DH⊥EF于H,
则四边形DCEH是矩形,
∴HE=CD=10,CE=DH,
∴FH=x 10,
∵∠FDH=α=45°,
∴DH=FH=x 10,
∴CE=x 10,
∵tanβ=tan50°==,
∴x=(x 10)tan 50°,
故选:A.
【点睛】本题考查了解直角三角形的应用,由实际问题抽象出边角关系的等式,正确的识别图形是解题的关键.
13.18
【分析】由已知得∠β=30,∠BDA=90°,AC=48解Rt△CDA求出AD,DC
此时在△ADB中可求出BD的长,观察图形可知BC=BD-CD.
【详解】∵ ∠CDA=90° AC=48 β=30°
∴ CD=sinα×AC=24 (三角函数定义)
AD=cosα×AC=24× (三角函数定义)
∵ ∠BDA=90° ,∠α=45°
∴ tanα==1 (三角函数定义)
∴ BD=24×
∴ BC=24× 24≈18
即井架高BC为18米.
【点睛】本题考查解直角三角形的应用,解题的关键是根据特殊角度的三角函数的知识分别得出AD、DC和BD的长.
14.100.
【详解】由题意得,∠BCA=90°,∠BAC=30°,AB=200米,
∴BC=AB=100米.
15.
【分析】先求解 再利用线段的和差可得答案.
【详解】解:由题意可得:
同理:
故答案为:
【点睛】本题考查的是锐角的正切的应用,二次根式的减法运算,掌握“利用锐角的正切求解三角形的边长”是解本题的关键.
16.
【分析】当点M与点B重合时,EF垂直平分AB,利用三角函数即可求得EF的长;根据折叠的性质可知,AF=FM,若DF取最大值,则FM取最小值,即为边AD与BC的距离DG,即可求解.
【详解】解:当点M与点B重合时,由折叠的性质知EF垂直平分AB,
∴AE=EB=AB=3,
在Rt△AEF中,∠A=60°,AE=3,
tan60°=,
∴EF=3;
当AF长取得最小值时,DF长取得最大值,
由折叠的性质知EF垂直平分AM,则AF=FM,
∴FM⊥BC时,FM长取得最小值,此时DF长取得最大值,
过点D作DG⊥BC于点C,则四边形DGMF为矩形,
∴FM=DG,
在Rt△DGC中,∠C=∠A=60°,DC=AB=6,
∴DG=DCsin60°=3,
∴DF长的最大值为AD-AF=AD-FM=AD-DG=6-3,
故答案为:3;6-3.
【点睛】本题考查了菱形的性质,折叠的性质,解直角三角形,解题的关键是灵活运用所学知识解决问题.
17.233m
【分析】作AD⊥BC交CB的延长线于D,设AD为x,表示出DB和DC,根据正切的概念求出x的值即可.
【详解】解:作AD⊥BC交CB的延长线于D,设AD为x,
由题意得,∠ABD=45°,∠ACD=35°,
在Rt△ADB中,∠ABD=45°,
∴DB=x,
在Rt△ADC中,∠ACD=35°,
,
,
解得,x≈233.
所以,热气球离地面的高度约为233米.
故答案为:233.
【点睛】本题考查的是解直角三角形的应用,理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键,解答时,注意正确作出辅助线构造直角三角形.
18.这个标志性建筑物底部A到岸边的最短距离为公里.
【分析】题目主要考查解直角三角形的应用及垂线的性质,根据题意,作出辅助线,熟练掌握运用解三角形是解题关键.
要求这个标志性建筑物底部A到岸边的最短距离也就是要求出点A到直线的最短距离,过点A作于D,然后利用所给条件求出的长即可.
【详解】解:过A作于D,则的长度就是A到岸边的最短距离.
在中,,设,则,
在中,,
由,即,
所以,
又,即,
所以,
解得.
答:这个标志性建筑物底部A到岸边的最短距离为公里.
19.(1)∠A=60°,∠B=30°,c=4;(2) b=24,∠A=∠B=45°.
【详解】试题分析:
(1)由tanA=,可得∠A=30°,从而可得∠B=60°,再由c=2b可得c=;
(2)由勾股定理可得:b=24,由tanA=可得∠A=45°,从而可得∠B=45°.
试题解析:
(1)∵在Rt△ ABC中,tanA=,
∴tanA==,
∴∠A=60°,∠B=90°-60°=30°,
∴c=2b=2×2=4;
(2)∵在Rt△ABC中,根据勾股定理有b2=c2-a2,
∴b=24,
∴ tanA==1,
∴∠A=∠B=45°.
20.AD的长为6.5 m.
【分析】设电子警察安装在悬臂灯杆上的高度AD的长为xm.通过解Rt△ADB和Rt△ACD求得BD、CD的长度,然后结合BC=CD﹣BD列出方程,并解答.
【详解】设电子警察安装在悬臂灯杆上的高度AD的长为x m.
在Rt△ADB中,tan∠ABD= ,
∴BD=,
在Rt△ACD中,tan∠ACD= ,
∴CD=,
∵BC=CD﹣BD,
∴﹣=6,
∴4x﹣x=6.
解这个方程,得x=6.5.
答:电子警察安装在悬臂灯杆上的高度AD的长为6.5 m.
【点睛】本题考查的是解直角三角形的应﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.
21.(1)①,;②仍然成立,证明见解析;(2),理由见解析.
【分析】(1)①如图1中,连接BE,设DE交AB于T.首先证明再利用直角三角形斜边中线的性质解决问题即可.②解法一:如图2﹣1中,取AB的中点M,BE的中点N,连接CM,MN.证明(SAS),可得结论.解法二:如图2﹣2中,取DE的中点G,连接AG,CG,并把绕点C逆时针旋转90°得到,连接DT,GT,BG.证明四边形BEGT是平行四边形,四边形DGBT是平行四边形,可得结论.
(2)结论:BE=.如图3中,取AB的中点T,连接CT,FT.证明,可得结论.
【详解】解:(1)①如图1中,连接BE,设DE交AB于T.
∵CA=CB,∠CAB=45°,
∴∠CAB=∠ABC=45°,
∴∠ACB=90°,
∵∠ADE=∠ACB=45°,∠DAE=90°,
∴∠ADE=∠AED=45°,
∴AD=AE,
∴AT⊥DE,DT=ET,
∴AB垂直平分DE,
∴BD=BE,
∵∠BCD=90°,DF=FB,
∴CF=BD,
∴CF=BE.
故答案为:∠EAB=∠ABC,CF=BE.
②结论不变.
解法一:如图2﹣1中,取AB的中点M,BE的中点N,连接CM,MN.
∵∠ACB=90°,CA=CB,AM=BM,
∴CM⊥AB,CM=BM=AM,
由①得:
设AD=AE=y.FM=x,DM=a,
点F是BD的中点,
则DF=FB=a+x,
∵AM=BM,
∴y+a=a+2x,
∴y=2x,即AD=2FM,
∵AM=BM,EN=BN,
∴AE=2MN,MN∥AE,
∴MN=FM,∠BMN=∠EAB=90°,
∴∠CMF=∠BMN=90°,
∴(SAS),
∴CF=BN,
∵BE=2BN,
∴CF=BE.
解法二:如图2﹣2中,取DE的中点G,连接AG,CG,并把△CAG绕点C逆时针旋转90°得到,连接DT,GT,BG.
∵AD=AE,∠EAD=90°,EG=DG,
∴AG⊥DE,∠EAG=∠DAG=45°,AG=DG=EG,
∵∠CAB=45°,
∴∠CAG=90°,
∴AC⊥AG,
∴AC∥DE,
∵∠ACB=∠CBT=90°,
∴AC∥BT∥,
∵AG=BT,
∴DG=BT=EG,
∴四边形BEGT是平行四边形,四边形DGBT是平行四边形,
∴BD与GT互相平分,
∵点F是BD的中点,
∴BD与GT交于点F,
∴GF=FT,
由旋转可得;
是等腰直角三角形,
∴CF=FG=FT,
∴CF=BE.
(2)结论:BE=.
理由:如图3中,取AB的中点T,连接CT,FT.
∵CA=CB,
∴∠CAB=∠CBA=30°,∠ACB=120°,
∵AT=TB,
∴CT⊥AB,
∴AT=,
∴AB=,
∵DF=FB,AT=TB,
∴TF∥AD,AD=2FT,
∴∠FTB=∠CAB=30°,
∵∠CTB=∠DAE=90°,
∴∠CTF=∠BAE=60°,
∵∠ADE=∠ACB=60°,
∴AE=AD=FT,
∴,
∴,
∴,
∴.
【点睛】本题属于相似形综合题,考查了等腰三角形的性质,全等三角形的判定和性质,平行四边形的判定和性质,相似三角形的判定和性质,锐角三角函数的应用,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.
22.BC=2(+1).
【详解】试题分析:由题意可得△BCD为等腰直角三角形,从而BD=BC,在Rt△ABC中,由∠A的正切值可求出BC的长.
试题解析:∵∠B=90°,∠BDC=45°,
∴△BCD为等腰直角三角形,
∴BD=BC,
在Rt△ABC中,tanA=tan30°=,即,
解得:BC=2(+1).
考点: 解直角三角形
23.受到污染;30s
【分析】问教室A是否在拖拉机的噪声污染范围内,其实就是问A到OM的距离是否大于污染半径125m,如果大于则不受影响,反之则受影响.如果过A作AB⊥OM于B,那么AB就是所求的线段.直角三角形AOB中,∠AOB的度数容易求得,又已知了OA的值,那么AB便可求出了.然后进行判断即可.
如果设拖拉机从C到D教室受影响,那么要求教室受影响的时间,其实就是求CD的值,直角三角形ABC中,AB的值已经求得.又有AC的值,那么BC的值就能求出了.CD也就能求出了,然后根据时间=路程÷速度即可得出时间是多少.
【详解】解:如图,过点A作AB⊥OM于点B,
∵∠MON=60°,
∴∠AOM=90°-60°=30°.
在Rt△ABO中,∠ABO=90°,
∵sin∠AOB=,
∴AB=AO sin∠AOB=200×sin30°=100(m).
∵100m<125m.
∴教室A在拖拉机的噪声污染范围内.
根据题意,在OM上取C,D两点,连接AC,AD,使AC=AD=125m,
∵AB⊥OM,
∴B为CD的中点,即BC=DB,
∴BC===75(m),
∴CD=2BC=150(m).
即影响的时间为=30s.
【点睛】本题主要考查了解直角三角形的知识,解题的关键是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.
24.米
【分析】本题考查了解直角三角形的应用—坡度坡角问题.解题的关键是正确作出辅助线,构造直角三角形求解.
过A点作于E.在中,根据三角函数可得,,在中,根据三角函数可得,再根据即可求解.
【详解】解:过A点作于E.
在中,.
∴米,米,
在中,,
∴米,
∴米.
故此时应将坝底向外拓宽大约米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
