3.1用字母表示数暑假预习练(含解析) 北师大版数学七年级上册
文档属性
| 名称 | 3.1用字母表示数暑假预习练(含解析) 北师大版数学七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 619.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.1用字母表示数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个两位数,它的十位数字是,个位数字是,那么这个两位数是( ).
A. B. C. D.
2.有一组数:,它们是按一定规律排列的,这一组数的第n个数是( )
A. B. C. D.
3.设n为整数,下列式子中表示偶数的是( ).
A. B. C. D.
4.下列是一组按一定规律排列的数: ,则第2019个数是( )
A. B. C. D.4039
5.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出9千克大米放入乙袋,那么甲、乙两袋质量相等.列成等式是( ).
A. B. C. D.
6.设n为整数,下列式子中表示偶数的是( ).
A. B. C. D.
7.用表示的数一定是( )
A.负数 B.正数或负数 C.0或负数 D.以上全不对
8.夏明今年a岁了,爸爸比夏明大21岁,则6年后,爸爸比夏明大( )岁.
A. B.21 C. D.6
9.(代数式应用)一个两位数,十位上的数字是a,个位上的数字是6,表示这个两位数的式子是( )
A. B. C. D.
10.如图,图中的三角形是有规律地从里到外逐层排列的,设N为第n层(n为自然数)三角形的个数,则下列函数表达式中正确的是( )
A. B.
C. D.
11.若b是有理数,则( )
A.b一定是正数 B.b正数,负数,0均有可能
C.一定是负数 D.b一定是0
12.如图图形都是由同样大小的“○”按- -定的规律组成,其中第1个图形中一共有5个“○”,第2个图形中一共有12个“○”,第3个图形中一共有21个“○”,……,则第7个图形中“○”的个数是( )
A.60 B.66 C.77 D.96
二、填空题
13.现有5元面值人民币m张,10元面值人民币n张,共有人民币 元(用含m、n的代数式表示).
14.古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数;
图形 …
五边形数 1 5 12 22 35 51 …
将五边形数1,5,12,22,35,51,…,排成如下数表;
1 第一行
5 12 第二行
22 35 51 第三行
… … … … …
观察这个数表,则这个数表中的第八行从左至右第2个数为 .
15.观察下列各式:12+1=1×2,22+2=2×3,32+3=3×4…,按此规律写出第n个等式 .
16.用字母表示数时需注意:(1)在同一问题中,同一字母只能表示 数量,不同的数量要用不同的字母表示;(2)用字母表示实际问题中某一数量时,字母的取值必须使这个问题 ,并且符合实际;(3)只要是学过的公式、法则,都可以用 表示;(4)字母“π”一般来说只表示一种量:圆周率;(5)对于用字母表示的数,如果没有特别说明,就应理解为它可以是任何一个数.
17.一组按规律排列的式子:,其中第7个式子是 ,第n个式子是 (n为正整数).
三、解答题
18.某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆形内部由三根等长的木条分隔,下部是用木条围成的边长相等的四个小正方形,木条的宽度和厚度不计.已知下部每个小正方形的边长为a米.
(1)用含a的代数式分别表示窗户的面积和所用木条的总长度;
(2)若米,窗户上安装的是玻璃,玻璃25元/平方米,木条20元/米,求制作这个窗户需要的总钱数(值取3,计算结果精确到个位).
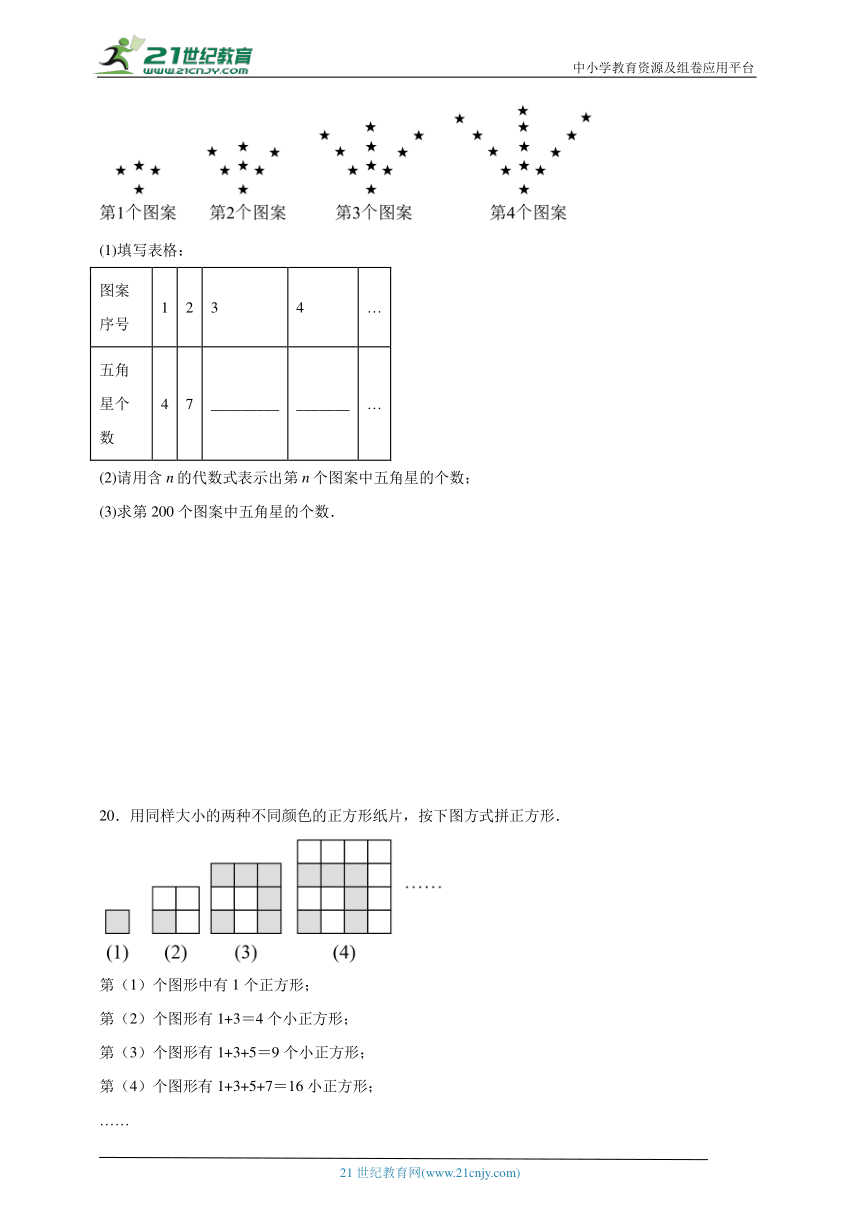
19.按如下规律摆放五角星:
(1)填写表格:
图案序号 1 2 3 4 …
五角星个数 4 7 _________ _______ …
(2)请用含n的代数式表示出第n个图案中五角星的个数;
(3)求第200个图案中五角星的个数.
20.用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)=______(用含n的代数式表示);
(2)请根据你的发现计算:
①1+3+5+7+…+99;
②101+103+105+…+199.
21.观察下列等式:
①
②
③
……
(1)请写出第四个等式:___________﹔
(2)观察上述等式的规律,猜想第n个等式.(用含n的式子表示)
22.用字母表示图中阴影部分的面积.
23.对于密码L dp d vwxghqw,你能看出它代表什么意思吗?如果给你一把破译它的“钥匙”,联想英语字母表中字母的顺序,你再试试能不能解读它.英语字母表中字母是按以下顺序排列的:
a b c d e f g h i j k l m n o p q r s t u v w x y z
如果规定a又接在z的后面,使26个字母排成圈,并能想到可以代表“把一个字母换成字母表中从它向前移动3位的字母”,按这个规律就有
L dp d vwxghqw→I am a student.
这样你就能解读它的意思了.
为了保密,许多情况下都要采用密码,这时就需要有破译密码的“钥匙”.上面的例子中,如果写和读密码的双方事先约定了作为“钥匙”的式子的含义,那么他们就可以用一种保密方式通信了.你和同伴不妨也利用数学式子来制定一种类似的“钥匙”,并互相合作,通过游戏试试如何进行保密通信.
24.计算2021个连续自然数1、2、3、……、2019、2020、2021的和,可以用下列方法:
先把以上这列数写成2021、2020、……、3、2、1,再把这两列数的第一项和第一项相加、第二项和第二项相加、第三项和第三项相加、……倒数第三项和倒数第三项相加、倒数第二项和倒数第二项相加、倒数第一项和倒数第一项相加,可以得到以下解法:
解:
所以
通过阅读以上解法,计算下列各题(结果用含有的代数式表示):
(1)求连续自然数1、2、3、……、的和;
(2)求连续奇数1、3、5、……、的和.
《3.1用字母表示数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A B B A D B D B
题号 11 12
答案 B C
1.D
【分析】根据两位数的表示方法:十位数字个位数字,即可解答.
【详解】解:∵一个两位数,它的十位数是,个位数字是,
∴根据两位数的表示方法,这个两位数表示为:.
故选:
【点睛】本题考查了用字母表示数的方法,会用含有字母的式子表示数量是解题的关键.
2.C
【分析】根据题目中的数字,可以发现数字的分子和分母的变化特点,从而可以写出第n个数.
【详解】解:一组数为
∴这组数据第1个数为:,
第2个数为:,
第3个数为:
…
∴第n个数为:
故选:C
【点睛】本题考查数字的变化类,解答本题的关键是明确题意,发现数字的变化特点,写出相应的数字.
3.A
【分析】本题考查列代数式,掌握能被2整除的数是偶数和代数式的书写要求是解题的关键.
根据偶数的定义,列出代数式即可.
【详解】解:∵偶数是2的倍数,
∴用(n为整数)表示偶数,
故选:A.
4.B
【分析】找出数据的排列规律即可得.
【详解】解:根据题意可知数据的排列规律是,…,所以第2019个数是,
故选B.
【点睛】本题考查了数字排列的规律,解题的关键是找出所给数据的排列规律.
5.B
【分析】根据题意,找出数量关系,即可而出等式.
【详解】解:根据题意可得:
,
故选:B.
【点睛】本题主要考查了用字母表示数,解题的关键是正确理解题意,根据题意找出等量关系列出等式.
6.A
【解析】略
7.D
【分析】本题主要考查用字母可以表示数,既可以是正数,也可以是负数和0,带有负号的数不一定就是负数.
【详解】解:A、当为非正数时,则表示的数是非负数,故此选项不符合题意;
B、当时,,即此时表示的数既不是负数,也不是正数,故此选项不符合题意;
C、当时,,即此时表示正数,故此选项不符合题意;
综上所述,表示的数可以是负数,正数或0.
故选D.
8.B
【分析】本题题考查的是用字母表示数,熟练掌握用字母表示数及数量关系是解题的关键.
根据夏明今年a岁了,爸爸比夏明大21岁,分别用含有字母的式子表示出爸爸今年的岁数、夏明6年后的岁数、爸爸6年后的岁数,用减法即可计算出爸爸6年后比夏明大的岁数.本题还可以根据“年龄差不变”直接得出答案.
【详解】爸爸今年:岁;
6年后,夏明岁;
爸爸:岁;
爸爸比夏明大:
(岁);
故答案为:B
9.D
【分析】本题考查列代数式,解决问题的关键是读懂题意,掌握两位数=十位数字个位数字.
根据:两位数=十位数字×10+个位数字,代入数值,解答即可.
【详解】解:;
故选:D.
10.B
【分析】根据图示可知,第一层是4个,第二层是8个,第三层是12,…第n层是4n,所以,即可确定N与n的关系.
【详解】解:由图可知:n=1时,三角形有4个,即N=4;
n=2时,三角形有8个,即N=8;
n=3时,三角形有12个,即N=12;
∴N=4n.
故选:B.
【点睛】本题主要考查了列代数式,有一定难度.解题的关键是根据图象找到点的排列规律.
11.B
【分析】根据有理数,逐一进行判定,即可解答.
【详解】解:A、b一定是正数,错误;例如当b=0时,b不是正数;
B、正确;
C、一定是负数,错误;例如当b=0时,不是负数;
D、因为有理数包括正数、负数、0,所以b不一定是0,错误;
故选:B.
【点睛】本题考查了用字母表示数,一个用字母表示的数,既可以是正数、0,也可以是负数.
12.C
【分析】先找到前三个图形中的规律,得到第n个图形中“○”的个数是n×(4+n),即可计算第7个图形中“○”的个数.
【详解】第1个图形中一共有5个,即1×(4+1),
第2个图形中一共有12个,即2×(4+2),
第3个图形中一共有21个,即3×(4+3),……,
∴第n个图形中“○”的个数是n×(4+n),
∴第7个图形中“○”的个数是7×(4+7)=77,
故选:C.
【点睛】本题考查图形与数字规律,是基础考点,掌握相关知识是解题关键.
13.
【分析】由5元面值人民币m张,可得人民币元,由10元面值人民币n张,可得人民币元,从而可得答案.
【详解】解:由题意得:共有人民币元,
故答案为:
【点睛】本题考查的是列代数式,掌握列代数式的方法是解题的关键.
14.1335
【分析】分析表格中的图形和五边形数之间的规律,再找到排成数表中五边形数和行数之间的规律.
【详解】解:由图形规律可知,第n个图形是一个由n个点为边长的等边三角形和一个长为n个点,宽为(n-1)个点的矩形组成,则第n个图形一共有个点,化简得,即第n个图形的五边形数为.
分析排成数表,结合图形可知:
第一行从左至右第1个数,是第1个图形的五边形数;
第二行从左至右第1个数,是第2个图形的五边形数;
第三行从左至右第1个数,是第4个图形的五边形数;
第四行从左至右第1个数,是第7个图形的五边形数;
…
∴第n行从左至右第1个数,是第 个图形的五边形数.
∴第八行从左至右第2个数,是第30个图形的五边形数.
第30个图形的五边形数为:.
故答案为:1335.
【点睛】本题是找规律题,解此题的关键是分析表格中的图形个数与五边形数,排成数表中的五边形数和行数,得出规律.
15.:n2+n=n×(n+1).
【分析】根据算式可发现一个数的平方加上它本身,等于这个数与这个数加1的积.
【详解】解:观察各式可知,第几个算式就是几的平方加几,等于等于这个数与这个数加1的积,
所以,第n个等式为:n2+n=n×(n+1),
故答案为:n2+n=n×(n+1).
【点睛】本题考查了用代数式表示规律,解题关键是准确分析题意,找到规律.
16. 同一 有意义 字母
【分析】根据字母表示数的注意事项逐一填写即可.
【详解】解:用字母表示数时需注意:(1)在同一问题中,同一字母只能表示同一数量,不同的数量要用不同的字母表示;(2)用字母表示实际问题中某一数量时,字母的取值必须使这个问题有意义,并且符合实际;(3)只要是学过的公式、法则,都可以用字母表示;(4)字母“π”一般来说只表示一种量:圆周率;(5)对于用字母表示的数,如果没有特别说明,就应理解为它可以是任何一个数.
故答案为:同一;有意义;字母.
【点睛】本题考查字母表示数的注意事项,在理解的基础上记忆是解题的关键.
17.
【分析】根据分子的变化得出分子变化的规律,根据分母的变化得出分母变化的规律,根据分数符号的变化规律得出分数符号的变化规律,即可得到该组式子的变化规律.
【详解】分子为b,指数为2,5,8,11,...,
分子指数的规律为3n – 1,
分母为a,指数为1,2,3,4,...,
分母指数的规律为n,
分数符号为-,+,-,+,….,
其规律为,
于是,第7个式子为,
第n个式子为,
故答案为:,.
【点睛】此题考查了列代数式表示数字变化规律,先根据分子、分母的变化得出规律,再根据分式符号的变化得出规律是解题的关键.
18.(1)窗户的面积为(4a2πa2)米2,总长度(15+π)a(米)
(2)498(元)
【分析】(1)窗户的面积包括一个正方形面积一个半圆面积,相加即可.材料总长度就是求图形中线段的总长度,将所有线段长度相加即可;
(2)将a=1代入25(4a2πa2)+20(15+π)a计算可得.
【详解】(1)S=2a×2aπa2=4a2πa2
即窗户的面积为(4a2πa2)米2.
15a+πa=(15+π)a(米)
即制作这种窗户所需材料的总长度(15+π)a(米).
(2)a=1时,25(4a2πa2)+20(15+π)a
≈25×(4×13×1)+20×(15+3)×1
=137.5+360
=497.5
≈498(元),即制作这扇窗户需要498元.
【点睛】本题考查了根据实际情况列代数式,一方面要掌握面积和周长的计算公式,另一方面要做好计算准确,不遗漏.
19.(1)10,13
(2)3n+1
(3)601
【分析】()观察图形规律数出个数即可;
(2)把五角星分成两部分,顶点处的一个不变,其它的分三条线,每一条线上后一个图形比前一个图形多一个,根据此规律找出第n个图形中五角星的个数的关系式为3n+1;
(3)将n=20代入3n+1解答即可;
【详解】(1)解:观察图形规律:
第一个图形有4个五角星,
第二个图形比第一个图形多3个五角星,即有4+3=7个五角星,
第三个图形比第二个图形多3个五角星,即有4+3+3=10个五角星,
故答案为:10,13;
(2)解:观察图形规律:
第一个图形有4个五角星,
第二个图形比第一个图形多3个五角星,即有4+3=7个五角星,
第三个图形比第二个图形多3个五角星,即有4+3+3=10个五角星,
第四个图形比第三个图形多3个五角星,即有4+3+3+3=13个五角星,
…………
以此类推,第n个图形中的五角星有4+3(n﹣1)=(3n+1)个五角星,
(3)解:将n=200代入3n+1中,得3×200+1=601(个).
【点睛】本题考查了图形变化规律的问题,把五角星分成两部分进行考虑,并找出第n个图形五角星的个数的表达式是解题的关键.
20.(1)n2
(2)①1+3+5+7+…+99=2500;②101+103+105+…+199=7500
【分析】(1)观察图形的变化可得规律,根据发现的规律即可猜想1+3+5+7+…+(2n-1)的值;
(2)①根据(1)中的规律即可求解;②根据(1)中的规律和①的结果,即可求得101+103+105+…+199的值.
【详解】(1)解:∵第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
∴1+3+5+7+…+(2n﹣1)
=()2
=n2;
故答案为:n2;
(2)解:①1+3+5+7+…+99
=()2
=502
=2500;
②∵1+3+5+7+…+199
=()2
=10000,
∴101+103+105+…+199
=10000﹣2500
=7500.
【点睛】本题考查了规律型-图形的变化类,解决本题的关键是观察图形的变化寻找规律.
21.(1);(2)
【分析】(1)把前三个等式都看作减法算式的话,每个算式的被减数分别是1,2,3,减数的分母分别是6=1+5,7=2+5,8=3+5,减数的分子分别是5=51,10=52,15=53,差分别是被减数的平方和以减数的分母作分母,以1作分子的分数的差;据此判断出第四个等式的被减数是4,减数的分母是9,分子是5的4倍,差等于4与的乘积;
(2)根据上述等式的规律,猜想第n个等式为:=,然后把等式的左边化简,根据左边=右边,证明等式的准确性即可.
【详解】解:(1)把前三个等式左边都看作减法算式的话,每个算式的被减数分别是1,2,3,减数的分母分别是6=1+5,7=2+5,8=3+5,减数的分子分别是5=51,10=52,15=53;右边分别是被减数的平方和以减数的分母作分母,以1作分子的分数的差;据此判断出第四个等式的被减数是4,减数的分母是9,分子是5的4倍,差等于4与的乘积;
∴第四个等式为:4-=42×;
(2)猜想:=(其中n为正整数).
验证:n-==,所以左式=右式,所以猜想成立.
【点睛】此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出::第n个等式为:=.
22.(1)ab﹣bx;(2)R2πR2
【分析】(1)读图可得,阴影部分的面积=大长方形的面积﹣小长方形的面积;
(2)阴影部分的面积=正方形的面积﹣扇形的面积.
【详解】解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2πR2.
【点睛】本题考查代数式的应用,解决问题的关键是看懂图,找到所求的阴影部分的面积和各部分之间的等量关系.
23.答案见解析
【分析】可以根据自己的喜好利用数学式子来制定一种类似的“钥匙”,比如说,然后写上一句话,比如“study well and make progress every day”,根据题干中的方式,自己先利用秘钥x+2将这句话变成密码文字“uvwfa ygnn cpf ocmg rtqitguu gxgta fca”,然后再让同伴破译.
【详解】解:可设置秘钥,
密码为:uvwfa ygnn cpf ocmg rtqitguu gxgta fca,
破译后的文字为:study well and make progress every day.
(学生可尝试自己制定,本题答案不唯一)
【点睛】本题考查探索与表达规律.能读懂题意,得出题例中制定的制定规律是解题关键.
24.(1)n(n+1)
(2)(n+1)2
【分析】(1)根据题目中的方法进行求解即可;
(2)仿照题目中的方法进行求解即可.
【详解】(1)解:由题意得:
1+2+3+…+(n-2)+(n-1)+n=n(n+1);
(2)1+3+5+…+(2n+1)
=×(1+2n+1)(n+1)
=(n+1)2.
【点睛】本题主要考查规律型:数字的变化类,列代数式,解答的关键是总结出存在的规律.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.1用字母表示数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个两位数,它的十位数字是,个位数字是,那么这个两位数是( ).
A. B. C. D.
2.有一组数:,它们是按一定规律排列的,这一组数的第n个数是( )
A. B. C. D.
3.设n为整数,下列式子中表示偶数的是( ).
A. B. C. D.
4.下列是一组按一定规律排列的数: ,则第2019个数是( )
A. B. C. D.4039
5.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出9千克大米放入乙袋,那么甲、乙两袋质量相等.列成等式是( ).
A. B. C. D.
6.设n为整数,下列式子中表示偶数的是( ).
A. B. C. D.
7.用表示的数一定是( )
A.负数 B.正数或负数 C.0或负数 D.以上全不对
8.夏明今年a岁了,爸爸比夏明大21岁,则6年后,爸爸比夏明大( )岁.
A. B.21 C. D.6
9.(代数式应用)一个两位数,十位上的数字是a,个位上的数字是6,表示这个两位数的式子是( )
A. B. C. D.
10.如图,图中的三角形是有规律地从里到外逐层排列的,设N为第n层(n为自然数)三角形的个数,则下列函数表达式中正确的是( )
A. B.
C. D.
11.若b是有理数,则( )
A.b一定是正数 B.b正数,负数,0均有可能
C.一定是负数 D.b一定是0
12.如图图形都是由同样大小的“○”按- -定的规律组成,其中第1个图形中一共有5个“○”,第2个图形中一共有12个“○”,第3个图形中一共有21个“○”,……,则第7个图形中“○”的个数是( )
A.60 B.66 C.77 D.96
二、填空题
13.现有5元面值人民币m张,10元面值人民币n张,共有人民币 元(用含m、n的代数式表示).
14.古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数;
图形 …
五边形数 1 5 12 22 35 51 …
将五边形数1,5,12,22,35,51,…,排成如下数表;
1 第一行
5 12 第二行
22 35 51 第三行
… … … … …
观察这个数表,则这个数表中的第八行从左至右第2个数为 .
15.观察下列各式:12+1=1×2,22+2=2×3,32+3=3×4…,按此规律写出第n个等式 .
16.用字母表示数时需注意:(1)在同一问题中,同一字母只能表示 数量,不同的数量要用不同的字母表示;(2)用字母表示实际问题中某一数量时,字母的取值必须使这个问题 ,并且符合实际;(3)只要是学过的公式、法则,都可以用 表示;(4)字母“π”一般来说只表示一种量:圆周率;(5)对于用字母表示的数,如果没有特别说明,就应理解为它可以是任何一个数.
17.一组按规律排列的式子:,其中第7个式子是 ,第n个式子是 (n为正整数).
三、解答题
18.某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆形内部由三根等长的木条分隔,下部是用木条围成的边长相等的四个小正方形,木条的宽度和厚度不计.已知下部每个小正方形的边长为a米.
(1)用含a的代数式分别表示窗户的面积和所用木条的总长度;
(2)若米,窗户上安装的是玻璃,玻璃25元/平方米,木条20元/米,求制作这个窗户需要的总钱数(值取3,计算结果精确到个位).
19.按如下规律摆放五角星:
(1)填写表格:
图案序号 1 2 3 4 …
五角星个数 4 7 _________ _______ …
(2)请用含n的代数式表示出第n个图案中五角星的个数;
(3)求第200个图案中五角星的个数.
20.用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)=______(用含n的代数式表示);
(2)请根据你的发现计算:
①1+3+5+7+…+99;
②101+103+105+…+199.
21.观察下列等式:
①
②
③
……
(1)请写出第四个等式:___________﹔
(2)观察上述等式的规律,猜想第n个等式.(用含n的式子表示)
22.用字母表示图中阴影部分的面积.
23.对于密码L dp d vwxghqw,你能看出它代表什么意思吗?如果给你一把破译它的“钥匙”,联想英语字母表中字母的顺序,你再试试能不能解读它.英语字母表中字母是按以下顺序排列的:
a b c d e f g h i j k l m n o p q r s t u v w x y z
如果规定a又接在z的后面,使26个字母排成圈,并能想到可以代表“把一个字母换成字母表中从它向前移动3位的字母”,按这个规律就有
L dp d vwxghqw→I am a student.
这样你就能解读它的意思了.
为了保密,许多情况下都要采用密码,这时就需要有破译密码的“钥匙”.上面的例子中,如果写和读密码的双方事先约定了作为“钥匙”的式子的含义,那么他们就可以用一种保密方式通信了.你和同伴不妨也利用数学式子来制定一种类似的“钥匙”,并互相合作,通过游戏试试如何进行保密通信.
24.计算2021个连续自然数1、2、3、……、2019、2020、2021的和,可以用下列方法:
先把以上这列数写成2021、2020、……、3、2、1,再把这两列数的第一项和第一项相加、第二项和第二项相加、第三项和第三项相加、……倒数第三项和倒数第三项相加、倒数第二项和倒数第二项相加、倒数第一项和倒数第一项相加,可以得到以下解法:
解:
所以
通过阅读以上解法,计算下列各题(结果用含有的代数式表示):
(1)求连续自然数1、2、3、……、的和;
(2)求连续奇数1、3、5、……、的和.
《3.1用字母表示数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A B B A D B D B
题号 11 12
答案 B C
1.D
【分析】根据两位数的表示方法:十位数字个位数字,即可解答.
【详解】解:∵一个两位数,它的十位数是,个位数字是,
∴根据两位数的表示方法,这个两位数表示为:.
故选:
【点睛】本题考查了用字母表示数的方法,会用含有字母的式子表示数量是解题的关键.
2.C
【分析】根据题目中的数字,可以发现数字的分子和分母的变化特点,从而可以写出第n个数.
【详解】解:一组数为
∴这组数据第1个数为:,
第2个数为:,
第3个数为:
…
∴第n个数为:
故选:C
【点睛】本题考查数字的变化类,解答本题的关键是明确题意,发现数字的变化特点,写出相应的数字.
3.A
【分析】本题考查列代数式,掌握能被2整除的数是偶数和代数式的书写要求是解题的关键.
根据偶数的定义,列出代数式即可.
【详解】解:∵偶数是2的倍数,
∴用(n为整数)表示偶数,
故选:A.
4.B
【分析】找出数据的排列规律即可得.
【详解】解:根据题意可知数据的排列规律是,…,所以第2019个数是,
故选B.
【点睛】本题考查了数字排列的规律,解题的关键是找出所给数据的排列规律.
5.B
【分析】根据题意,找出数量关系,即可而出等式.
【详解】解:根据题意可得:
,
故选:B.
【点睛】本题主要考查了用字母表示数,解题的关键是正确理解题意,根据题意找出等量关系列出等式.
6.A
【解析】略
7.D
【分析】本题主要考查用字母可以表示数,既可以是正数,也可以是负数和0,带有负号的数不一定就是负数.
【详解】解:A、当为非正数时,则表示的数是非负数,故此选项不符合题意;
B、当时,,即此时表示的数既不是负数,也不是正数,故此选项不符合题意;
C、当时,,即此时表示正数,故此选项不符合题意;
综上所述,表示的数可以是负数,正数或0.
故选D.
8.B
【分析】本题题考查的是用字母表示数,熟练掌握用字母表示数及数量关系是解题的关键.
根据夏明今年a岁了,爸爸比夏明大21岁,分别用含有字母的式子表示出爸爸今年的岁数、夏明6年后的岁数、爸爸6年后的岁数,用减法即可计算出爸爸6年后比夏明大的岁数.本题还可以根据“年龄差不变”直接得出答案.
【详解】爸爸今年:岁;
6年后,夏明岁;
爸爸:岁;
爸爸比夏明大:
(岁);
故答案为:B
9.D
【分析】本题考查列代数式,解决问题的关键是读懂题意,掌握两位数=十位数字个位数字.
根据:两位数=十位数字×10+个位数字,代入数值,解答即可.
【详解】解:;
故选:D.
10.B
【分析】根据图示可知,第一层是4个,第二层是8个,第三层是12,…第n层是4n,所以,即可确定N与n的关系.
【详解】解:由图可知:n=1时,三角形有4个,即N=4;
n=2时,三角形有8个,即N=8;
n=3时,三角形有12个,即N=12;
∴N=4n.
故选:B.
【点睛】本题主要考查了列代数式,有一定难度.解题的关键是根据图象找到点的排列规律.
11.B
【分析】根据有理数,逐一进行判定,即可解答.
【详解】解:A、b一定是正数,错误;例如当b=0时,b不是正数;
B、正确;
C、一定是负数,错误;例如当b=0时,不是负数;
D、因为有理数包括正数、负数、0,所以b不一定是0,错误;
故选:B.
【点睛】本题考查了用字母表示数,一个用字母表示的数,既可以是正数、0,也可以是负数.
12.C
【分析】先找到前三个图形中的规律,得到第n个图形中“○”的个数是n×(4+n),即可计算第7个图形中“○”的个数.
【详解】第1个图形中一共有5个,即1×(4+1),
第2个图形中一共有12个,即2×(4+2),
第3个图形中一共有21个,即3×(4+3),……,
∴第n个图形中“○”的个数是n×(4+n),
∴第7个图形中“○”的个数是7×(4+7)=77,
故选:C.
【点睛】本题考查图形与数字规律,是基础考点,掌握相关知识是解题关键.
13.
【分析】由5元面值人民币m张,可得人民币元,由10元面值人民币n张,可得人民币元,从而可得答案.
【详解】解:由题意得:共有人民币元,
故答案为:
【点睛】本题考查的是列代数式,掌握列代数式的方法是解题的关键.
14.1335
【分析】分析表格中的图形和五边形数之间的规律,再找到排成数表中五边形数和行数之间的规律.
【详解】解:由图形规律可知,第n个图形是一个由n个点为边长的等边三角形和一个长为n个点,宽为(n-1)个点的矩形组成,则第n个图形一共有个点,化简得,即第n个图形的五边形数为.
分析排成数表,结合图形可知:
第一行从左至右第1个数,是第1个图形的五边形数;
第二行从左至右第1个数,是第2个图形的五边形数;
第三行从左至右第1个数,是第4个图形的五边形数;
第四行从左至右第1个数,是第7个图形的五边形数;
…
∴第n行从左至右第1个数,是第 个图形的五边形数.
∴第八行从左至右第2个数,是第30个图形的五边形数.
第30个图形的五边形数为:.
故答案为:1335.
【点睛】本题是找规律题,解此题的关键是分析表格中的图形个数与五边形数,排成数表中的五边形数和行数,得出规律.
15.:n2+n=n×(n+1).
【分析】根据算式可发现一个数的平方加上它本身,等于这个数与这个数加1的积.
【详解】解:观察各式可知,第几个算式就是几的平方加几,等于等于这个数与这个数加1的积,
所以,第n个等式为:n2+n=n×(n+1),
故答案为:n2+n=n×(n+1).
【点睛】本题考查了用代数式表示规律,解题关键是准确分析题意,找到规律.
16. 同一 有意义 字母
【分析】根据字母表示数的注意事项逐一填写即可.
【详解】解:用字母表示数时需注意:(1)在同一问题中,同一字母只能表示同一数量,不同的数量要用不同的字母表示;(2)用字母表示实际问题中某一数量时,字母的取值必须使这个问题有意义,并且符合实际;(3)只要是学过的公式、法则,都可以用字母表示;(4)字母“π”一般来说只表示一种量:圆周率;(5)对于用字母表示的数,如果没有特别说明,就应理解为它可以是任何一个数.
故答案为:同一;有意义;字母.
【点睛】本题考查字母表示数的注意事项,在理解的基础上记忆是解题的关键.
17.
【分析】根据分子的变化得出分子变化的规律,根据分母的变化得出分母变化的规律,根据分数符号的变化规律得出分数符号的变化规律,即可得到该组式子的变化规律.
【详解】分子为b,指数为2,5,8,11,...,
分子指数的规律为3n – 1,
分母为a,指数为1,2,3,4,...,
分母指数的规律为n,
分数符号为-,+,-,+,….,
其规律为,
于是,第7个式子为,
第n个式子为,
故答案为:,.
【点睛】此题考查了列代数式表示数字变化规律,先根据分子、分母的变化得出规律,再根据分式符号的变化得出规律是解题的关键.
18.(1)窗户的面积为(4a2πa2)米2,总长度(15+π)a(米)
(2)498(元)
【分析】(1)窗户的面积包括一个正方形面积一个半圆面积,相加即可.材料总长度就是求图形中线段的总长度,将所有线段长度相加即可;
(2)将a=1代入25(4a2πa2)+20(15+π)a计算可得.
【详解】(1)S=2a×2aπa2=4a2πa2
即窗户的面积为(4a2πa2)米2.
15a+πa=(15+π)a(米)
即制作这种窗户所需材料的总长度(15+π)a(米).
(2)a=1时,25(4a2πa2)+20(15+π)a
≈25×(4×13×1)+20×(15+3)×1
=137.5+360
=497.5
≈498(元),即制作这扇窗户需要498元.
【点睛】本题考查了根据实际情况列代数式,一方面要掌握面积和周长的计算公式,另一方面要做好计算准确,不遗漏.
19.(1)10,13
(2)3n+1
(3)601
【分析】()观察图形规律数出个数即可;
(2)把五角星分成两部分,顶点处的一个不变,其它的分三条线,每一条线上后一个图形比前一个图形多一个,根据此规律找出第n个图形中五角星的个数的关系式为3n+1;
(3)将n=20代入3n+1解答即可;
【详解】(1)解:观察图形规律:
第一个图形有4个五角星,
第二个图形比第一个图形多3个五角星,即有4+3=7个五角星,
第三个图形比第二个图形多3个五角星,即有4+3+3=10个五角星,
故答案为:10,13;
(2)解:观察图形规律:
第一个图形有4个五角星,
第二个图形比第一个图形多3个五角星,即有4+3=7个五角星,
第三个图形比第二个图形多3个五角星,即有4+3+3=10个五角星,
第四个图形比第三个图形多3个五角星,即有4+3+3+3=13个五角星,
…………
以此类推,第n个图形中的五角星有4+3(n﹣1)=(3n+1)个五角星,
(3)解:将n=200代入3n+1中,得3×200+1=601(个).
【点睛】本题考查了图形变化规律的问题,把五角星分成两部分进行考虑,并找出第n个图形五角星的个数的表达式是解题的关键.
20.(1)n2
(2)①1+3+5+7+…+99=2500;②101+103+105+…+199=7500
【分析】(1)观察图形的变化可得规律,根据发现的规律即可猜想1+3+5+7+…+(2n-1)的值;
(2)①根据(1)中的规律即可求解;②根据(1)中的规律和①的结果,即可求得101+103+105+…+199的值.
【详解】(1)解:∵第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有1+3+5+7=16小正方形;
……
∴1+3+5+7+…+(2n﹣1)
=()2
=n2;
故答案为:n2;
(2)解:①1+3+5+7+…+99
=()2
=502
=2500;
②∵1+3+5+7+…+199
=()2
=10000,
∴101+103+105+…+199
=10000﹣2500
=7500.
【点睛】本题考查了规律型-图形的变化类,解决本题的关键是观察图形的变化寻找规律.
21.(1);(2)
【分析】(1)把前三个等式都看作减法算式的话,每个算式的被减数分别是1,2,3,减数的分母分别是6=1+5,7=2+5,8=3+5,减数的分子分别是5=51,10=52,15=53,差分别是被减数的平方和以减数的分母作分母,以1作分子的分数的差;据此判断出第四个等式的被减数是4,减数的分母是9,分子是5的4倍,差等于4与的乘积;
(2)根据上述等式的规律,猜想第n个等式为:=,然后把等式的左边化简,根据左边=右边,证明等式的准确性即可.
【详解】解:(1)把前三个等式左边都看作减法算式的话,每个算式的被减数分别是1,2,3,减数的分母分别是6=1+5,7=2+5,8=3+5,减数的分子分别是5=51,10=52,15=53;右边分别是被减数的平方和以减数的分母作分母,以1作分子的分数的差;据此判断出第四个等式的被减数是4,减数的分母是9,分子是5的4倍,差等于4与的乘积;
∴第四个等式为:4-=42×;
(2)猜想:=(其中n为正整数).
验证:n-==,所以左式=右式,所以猜想成立.
【点睛】此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出::第n个等式为:=.
22.(1)ab﹣bx;(2)R2πR2
【分析】(1)读图可得,阴影部分的面积=大长方形的面积﹣小长方形的面积;
(2)阴影部分的面积=正方形的面积﹣扇形的面积.
【详解】解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2πR2.
【点睛】本题考查代数式的应用,解决问题的关键是看懂图,找到所求的阴影部分的面积和各部分之间的等量关系.
23.答案见解析
【分析】可以根据自己的喜好利用数学式子来制定一种类似的“钥匙”,比如说,然后写上一句话,比如“study well and make progress every day”,根据题干中的方式,自己先利用秘钥x+2将这句话变成密码文字“uvwfa ygnn cpf ocmg rtqitguu gxgta fca”,然后再让同伴破译.
【详解】解:可设置秘钥,
密码为:uvwfa ygnn cpf ocmg rtqitguu gxgta fca,
破译后的文字为:study well and make progress every day.
(学生可尝试自己制定,本题答案不唯一)
【点睛】本题考查探索与表达规律.能读懂题意,得出题例中制定的制定规律是解题关键.
24.(1)n(n+1)
(2)(n+1)2
【分析】(1)根据题目中的方法进行求解即可;
(2)仿照题目中的方法进行求解即可.
【详解】(1)解:由题意得:
1+2+3+…+(n-2)+(n-1)+n=n(n+1);
(2)1+3+5+…+(2n+1)
=×(1+2n+1)(n+1)
=(n+1)2.
【点睛】本题主要考查规律型:数字的变化类,列代数式,解答的关键是总结出存在的规律.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
