2024-2025学年下学期小学数学人教版四年级暑假分层作业5.1三角形的特性(含解析)
文档属性
| 名称 | 2024-2025学年下学期小学数学人教版四年级暑假分层作业5.1三角形的特性(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 288.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 10:04:02 | ||
图片预览




文档简介
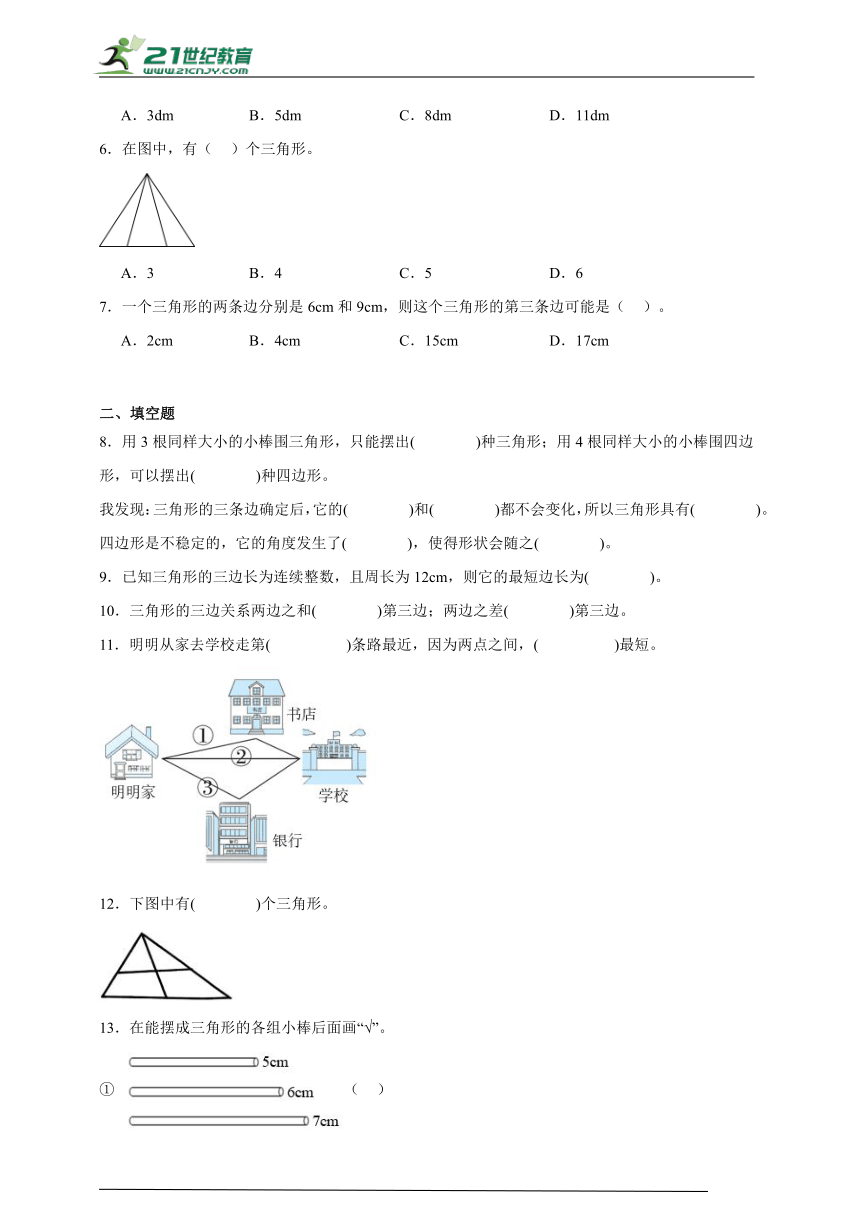
2024-2025学年下学期小学数学人教版四年级暑假分层作业5.1三角形的特性
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面( )组小棒可以围成一个三角形。
A.3cm、4cm、5cm B.2cm、6cm、8cm
C.5cm、5cm、12cm D.8cm、10cm、20cm
2.下面三角形中,底边对应的高的画法,正确的是( )。
A. B. C. D.
3.在( )处建桥可以使小南家到小宇家的距离最近。
A.A B.B C.C
4.下面每个盒子里都有两根小棒,把其中的一根小棒剪成两段,与另一根小棒围成一个三角形,能围成三角形的是( )。
A. B. C.
5.一个三角形两条边的长度分别是3dm、8dm,第三条边的长度可能是( )。
A.3dm B.5dm C.8dm D.11dm
6.在图中,有( )个三角形。
A.3 B.4 C.5 D.6
7.一个三角形的两条边分别是6cm和9cm,则这个三角形的第三条边可能是( )。
A.2cm B.4cm C.15cm D.17cm
二、填空题
8.用3根同样大小的小棒围三角形,只能摆出( )种三角形;用4根同样大小的小棒围四边形,可以摆出( )种四边形。
我发现:三角形的三条边确定后,它的( )和( )都不会变化,所以三角形具有( )。
四边形是不稳定的,它的角度发生了( ),使得形状会随之( )。
9.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )。
10.三角形的三边关系两边之和( )第三边;两边之差( )第三边。
11.明明从家去学校走第( )条路最近,因为两点之间,( )最短。
12.下图中有( )个三角形。
13.在能摆成三角形的各组小棒后面画“√”。
①( )
②( )
③( )
我发现:
(1)三角形任意两边之和( )。
(2)最快的方法判断:只要看( )两根的长度和是否大于第三边的长度。
14.下面两个框架中,( )不容易变形,因为( )具有稳定性。
15.用两根6厘米长的小棒和另一个小棒围成一个三角形(三条边的长都是整厘米数),另一根小棒最长是( )厘米,最短是( )厘米。
16.小丁准备把一根长10cm的细纸棍剪成3段围成三角形,如果第一次在4cm处剪了一刀(如图),第二次不能剪在( )处。(填A、B、C)
三、判断题
17.一个等腰三角形的两条边是5厘米、10厘米,那么它的周长可能是20厘米或25厘米。( )
18.小李家里的木桌子松动了,按下图的方法处理比较牢固,是利用了三角形具有稳定性的特性。( )
19.任意三条线段都可以围成(每相邻两条线段的端点相连)一个三角形。( )
20.用三条线段一定能拼成一个三角形。( )
21.如图,电线杆上有三角形,这是根据三角形的稳定性来设计的。( )
22.以下三根小棒能围成一个等腰三角形:6厘米、6厘米、12厘米。( )
23.一个三角形的两条边分别是3cm和4cm,第三边的长度不可能是8cm。( )
24.三角形具有稳定性,平行四边形也具有稳定性。( )
四、作图题
25.下面是一个梯形,把它分成一个三角形和一个梯形。
五、解答题
26.空调的室外机需要一个支架。王叔叔根据三角形的稳定性决定将其做成三角形形状。已经有两根铝合金,它们的长度分别是7分米和12分米,第三根铝合金最长是多少分米?(取整数)
27.如果一个三角形的两条边分别长4厘米和7厘米,另一条边可能是几厘米?(取整厘米数)
28.李大伯家的三角形菜地的两条边分别长6米和8米,你知道这个三角形菜地的第三条边可能是多少米吗?(第三条边是整米数,写出所有答案)
29.用下面的六根小棒,你能摆出几种三角形?请画一画。
《2024-2025学年下学期小学数学人教版四年级暑假分层作业5.1三角形的特性》参考答案
题号 1 2 3 4 5 6 7
答案 A B B B C D B
1.A
【分析】三角形三边关系指的是在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。据此解答。
【详解】A.因为,,符合三角形三边关系,所以可以围成三角形;
B.因为,不符合三角形任意两边之和大于第三边,所以不能围成三角形;
C.因为,不符合三角形任意两边之和大于第三边,所以不能围成三角形;
D.因为,不符合三角形任意两边之和大于第三边,所以不能围成三角形;
故答案为:A
2.B
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高。据此选择即可。
【详解】A.选项中所画高没有垂直于底边,不正确;
B.高经过顶点且垂直于底边,正确;
C.高垂直于底边,但没有经过顶点,不正确;
D.高没有垂直于底边且没有经过顶点,不正确。
底边对应的高的画法,正确的是选项B。
故答案为:B
3.B
【分析】根据三角形的特性:三角形的两边之和大于第三边,两边之差小于第三边,所以在点B处建桥小南家到小宇家的距离最近。据此解答即可。
【详解】由分析可知,在B处建桥可以使小南家到小宇家的距离最近。
故答案为:B
4.B
【分析】根据观察三个选项,只有B符合三角形的特性,任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【详解】根据三角形的特性:任意两边之和大于第三边,任意两边之差小于第三边,只有B符合。
故答案为:B
【点睛】解答本体的关键根据三角形的特性分析、解答。
5.C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边。以此答题即可。
【详解】根据分析可知:
83=5(dm)
8+3=11(dm)
那么这个三角形的第三条边大于5dm,小于11dm。
3<5=5<8<11=11
一个三角形两条边的长度分别是3dm、8dm,第三条边的长度可能是8dm。
故答案为:C
6.D
【分析】由三条边首尾依次连接组成的封闭图形是三角形。依次数出小三角形的个数,再数出组合的个数,解答即可。
【详解】单独的小三角形,有3个;由2个小三角形组成的三角形,有2个;由3个小三角形组成的三角形,有1个。
3+2+1=6(个)
一共有6个三角形。
故答案为:D
7.B
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】6+9=15(cm)
9-6=3(cm)
第三条边的长度应比15cm短,比3cm长。
A.2cm<3cm;
B.3cm <4cm<15cm;
C.15cm=15cm;
D.17cm>15cm;
这个三角形的第三条边可能是4cm。
故答案为:B
8. 1 无数 大小 形状 稳定性 变化 变化
【详解】用3根同样大小的小棒围三角形,只能摆出1种三角形;用4根同样大小的小棒围四边形,可以摆出无数种四边形。
我发现:三角形的三条边确定后,它的大小和形状都不会变化,所以三角形具有稳定性。
四边形是不稳定的,它的角度发生了变化,使得形状会随之变化。房屋梁做成三角形、摄影师用的三角支架、自行车的三角架都利用了三角形的稳定性;伸缩门和升降梯则是利用了四边形的不稳定性。
9.3cm/3厘米
【分析】连续的自然数之间,前一个数比后一个数少1,三角形的三边之和为三角形的周长,用12除以3,计算出三条边中间长度的边长是多少,再分别减1和加1,即可算出这另外两条边的长度分别是多少。据此解答。
【详解】12÷3=4(cm)
4-1=3(cm)
4+1=5(cm)
3<4<5
已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为3cm。
10. 大于 小于
【详解】三角形三条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边;
所以,三角形的三边关系两边之和大于第三边;两边之差小于第三边。
11. ② 线段
【分析】直线上任意两点之间的一段叫做线段。连接两点的线段的长度叫做两点间的距离。两点之间,线段最短;据此即可解答。
【详解】根据分析可知,明明从家去学校走第②条路最近,因为两点之间,线段最短。
【点睛】本题主要考查学生对线段特点的掌握和灵活运用。
12.6
【分析】先数单个三角形的,再数两个组合的,再数多个组合的,最后相加即可解答。
【详解】单个:2个
两个组合:3个
多个组合:1个
2+3+1
=5+1
=6(个)
即题图中有6个三角形。
13.①√;②√;③
(1)大于第三边
(2)较短
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边;较短的两根小棒长度和大于最长的小棒,这三根小棒就能摆成三角形;据此即可解答。
【详解】①5+6>13,可以摆成三角形。
( √ )
②5+5>5,可以摆成三角形。
( √ )
③4+4<10,不能摆成三角形。
( )
(1)三角形任意两边之和大于第三边。
(2)最快的方法判断:只要看较短两根的长度和是否大于第三边的长度。
【点睛】熟练掌握三角形三边之间的关系是解答本题的关键。
14. ② 三角形
【分析】根据三角形具有稳定性,解答此题即可。
【详解】根据分析可知,
②不容易变形,因为三角形具有稳定性。
【点睛】熟练掌握三角形的特性,是解答此题的关键。
15. 11 1
【分析】根据三角形三边关系:任意两边之和大于第三边,要使另一根小棒最长,则这根小棒的长度应比两根6厘米长的小棒长度和小1厘米,即(6+6-1)厘米;要使另一根小棒最短,则最长的边为6厘米,则这根小棒的长度加上6厘米的和应比6厘米至少大1厘米,即这根小棒的长度为(6+1-6)厘米;据此解答。
【详解】6+6-1
=12-1
=11(厘米)
6+1-6
=7-6
=1(厘米)
所以,用两根6厘米长的小棒和另一个小棒围成一个三角形(三条边的长都是整厘米数),另一根小棒最长是11厘米,最短是1厘米。
16.A
【分析】三角形的三边关系:三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此即可选择。
【详解】A处是5厘米,第一次在4厘米处剪了一刀,如果第二次剪A处,第二条边长为:,,三角形边的长度之和等于第三边;所以不能剪在A处。
17.×
【分析】在三角形中,任意的两边之和大于第三边,任意的两边之差小于第三边,先判断求出等腰三角形的腰长和底,再求出三角形的周长,据此解答。
【详解】当等腰三角形的腰等于5厘米时,5+5=10,不符合三角形的三边关系,所以三角形的腰等于10厘米,底等于5厘米,因此三角形的周长:10+10+5=25(厘米),周长不可能是20厘米,所以题目说法错误。
故答案为:×
18.√
【分析】三角形具有稳定性,生活中很多设计都是利用这一特性,如:自行车的车架是三角形的,篮球架上篮板的支架是三角形的,电线杆的支架是三角形的,上述物体中的三角形都能使物体更加稳固。
【详解】据分析可得:
小李家里的木桌子松动了,按上图的方法处理比较牢固,是利用了三角形具有稳定性的特性,故此说法正确。
故答案为:√
19.×
【分析】三条线段要想围成三角形,就得满足:三角形任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【详解】据分析可知:只有满足任意两条线段的和大于第三条线段的三条线段才能构成三角形。
故答案为:×
20.×
【分析】根据三角形的任意两边之和大于第三边,三角形两边之差小于第三边。所以并不是任意三条线段能围成一个三角形的,据此解答。
【详解】因为三条线段要组成三角形;
必须任意两条线段之和大于第三条线段,任意两条线段之差小于第三条线段;
比如三条线段分别是2、2、4,2+2=4,这样的三条线段并不能拼成一个三角形。
所以原题的说法错误。
故答案为:×
【点睛】本题考查了三角形的三边关系,是基础题,熟记三边关系是解题的关键。
21.√
【分析】从电线杠上看出有一个三角形,根据三角形的特性:三角形具有稳定性。即可解答本题。
【详解】为了使电线架在电线杆上更稳固,设计电线杆时根据了三角形的稳定性来设计。
故答案为:√
22.×
【分析】根据三角形的特性:两边之和大于第三边,两边之差小于第三边;进行解答即可。
【详解】6+6=12(厘米),不符合三角形的三边关系:任意两边之和大于第三边,所以用6厘米、6厘米、12厘米三根小棒不能围成一个等腰三角形。所以原题说法错误。
故答案为:×
23.√
【分析】根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,据此判断即可。
【详解】3+4=7cm,7cm<8cm,不能围成三角形。
一个三角形的两条边分别是3cm和4cm,第三边的长度不可能是8cm。原题说法正确,
故答案为:√
24.×
【分析】根据三角形的特性、平行四边形的特性,三角形具有稳定性,而平行四边形容易变形;据此判断。
【详解】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,例如:埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造;
平行四边形具有不稳定性,生活中也有广泛应用,例如:活动挂架,伸缩门等;所以原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握三角形、平行四边形的特性及应用。
25.见详解
【分析】因为梯形的一组对边平行,所以要分成一个梯形和一个三角形,就要用原来梯形一组平行的边,作为新梯形的一组对边,再连接梯形的上底一个顶点和下底上的一点(不要作梯形一条腰的平行线),即可得到一个梯形和一个三角形,解答即可。
【详解】画图如下:
【点睛】熟练掌握梯形、三角形的特征,是解答此题的关键。
26.18分米
【分析】三角形三边的关系:任意两边之和大于第三边,任意两边之差小于第三边;据此解答。
【详解】7+12=19(分米),19分米>18分米
12-7=5(分米),5分米<6分米
第三边长度大于6分米小于18分米,最长为18分米
答:第三根铝合金最长是18分米。
【点睛】掌握三角形三边的关系是解答本题的关键。
27.4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、10厘米
【分析】根据任意三角形的两边之和必须大于第三边,两边之差小于第三边,代入数据,即可解题。
【详解】由分析可知:
4+7=11(厘米)
7-4=3(厘米)
因此另一条边大于3厘米小于11厘米,可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、10厘米。
答:另一条边可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、10厘米。
28.3米、4米、5米、6米、7米、8米、9米、10米、11米、12米、13米
【分析】三角形三边之间的关系:三角形两边之和大于第三边,两边之差小于第三边;据此解答。
【详解】6+8=14(米)
8-6=2(米)
因此第三条边大于2米小于14米;又因为第三条边是整米数,所以第三条边可能是3米、4米、5米、6米、7米、8米、9米、10米、11米、12米、13米。
答:这个三角形菜地的第三条边可能是3米、4米、5米、6米、7米、8米、9米、10米、11米、12米、13米。
29.6种
【分析】根据三角形的任意两边之和大于第三边进行判断即可。
【详解】最短边是3厘米有以下可能:
3厘米、3厘米、4厘米,3+3=6(厘米),4<6,能构成三角形;
3厘米、3厘米、5厘米,3+3=6(厘米),5<6,能构成三角形;
3厘米、4厘米、5厘米,3+4=7(厘米),5<7,能构成三角形;
3厘米、5厘米、5厘米,3+5=8(厘米),5<8,能构成三角形。
最短边是4厘米有以下可能:
4厘米、5厘米、5厘米,4+5=9(厘米),5<9,能构成三角形。
最短边是5厘米有以下可能:
5厘米、5厘米、5厘米,5+5=10(厘米),5<10,能构成三角形。
4+1+1=6(种)
答:能围出6种三角形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.下面( )组小棒可以围成一个三角形。
A.3cm、4cm、5cm B.2cm、6cm、8cm
C.5cm、5cm、12cm D.8cm、10cm、20cm
2.下面三角形中,底边对应的高的画法,正确的是( )。
A. B. C. D.
3.在( )处建桥可以使小南家到小宇家的距离最近。
A.A B.B C.C
4.下面每个盒子里都有两根小棒,把其中的一根小棒剪成两段,与另一根小棒围成一个三角形,能围成三角形的是( )。
A. B. C.
5.一个三角形两条边的长度分别是3dm、8dm,第三条边的长度可能是( )。
A.3dm B.5dm C.8dm D.11dm
6.在图中,有( )个三角形。
A.3 B.4 C.5 D.6
7.一个三角形的两条边分别是6cm和9cm,则这个三角形的第三条边可能是( )。
A.2cm B.4cm C.15cm D.17cm
二、填空题
8.用3根同样大小的小棒围三角形,只能摆出( )种三角形;用4根同样大小的小棒围四边形,可以摆出( )种四边形。
我发现:三角形的三条边确定后,它的( )和( )都不会变化,所以三角形具有( )。
四边形是不稳定的,它的角度发生了( ),使得形状会随之( )。
9.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为( )。
10.三角形的三边关系两边之和( )第三边;两边之差( )第三边。
11.明明从家去学校走第( )条路最近,因为两点之间,( )最短。
12.下图中有( )个三角形。
13.在能摆成三角形的各组小棒后面画“√”。
①( )
②( )
③( )
我发现:
(1)三角形任意两边之和( )。
(2)最快的方法判断:只要看( )两根的长度和是否大于第三边的长度。
14.下面两个框架中,( )不容易变形,因为( )具有稳定性。
15.用两根6厘米长的小棒和另一个小棒围成一个三角形(三条边的长都是整厘米数),另一根小棒最长是( )厘米,最短是( )厘米。
16.小丁准备把一根长10cm的细纸棍剪成3段围成三角形,如果第一次在4cm处剪了一刀(如图),第二次不能剪在( )处。(填A、B、C)
三、判断题
17.一个等腰三角形的两条边是5厘米、10厘米,那么它的周长可能是20厘米或25厘米。( )
18.小李家里的木桌子松动了,按下图的方法处理比较牢固,是利用了三角形具有稳定性的特性。( )
19.任意三条线段都可以围成(每相邻两条线段的端点相连)一个三角形。( )
20.用三条线段一定能拼成一个三角形。( )
21.如图,电线杆上有三角形,这是根据三角形的稳定性来设计的。( )
22.以下三根小棒能围成一个等腰三角形:6厘米、6厘米、12厘米。( )
23.一个三角形的两条边分别是3cm和4cm,第三边的长度不可能是8cm。( )
24.三角形具有稳定性,平行四边形也具有稳定性。( )
四、作图题
25.下面是一个梯形,把它分成一个三角形和一个梯形。
五、解答题
26.空调的室外机需要一个支架。王叔叔根据三角形的稳定性决定将其做成三角形形状。已经有两根铝合金,它们的长度分别是7分米和12分米,第三根铝合金最长是多少分米?(取整数)
27.如果一个三角形的两条边分别长4厘米和7厘米,另一条边可能是几厘米?(取整厘米数)
28.李大伯家的三角形菜地的两条边分别长6米和8米,你知道这个三角形菜地的第三条边可能是多少米吗?(第三条边是整米数,写出所有答案)
29.用下面的六根小棒,你能摆出几种三角形?请画一画。
《2024-2025学年下学期小学数学人教版四年级暑假分层作业5.1三角形的特性》参考答案
题号 1 2 3 4 5 6 7
答案 A B B B C D B
1.A
【分析】三角形三边关系指的是在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。据此解答。
【详解】A.因为,,符合三角形三边关系,所以可以围成三角形;
B.因为,不符合三角形任意两边之和大于第三边,所以不能围成三角形;
C.因为,不符合三角形任意两边之和大于第三边,所以不能围成三角形;
D.因为,不符合三角形任意两边之和大于第三边,所以不能围成三角形;
故答案为:A
2.B
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高。据此选择即可。
【详解】A.选项中所画高没有垂直于底边,不正确;
B.高经过顶点且垂直于底边,正确;
C.高垂直于底边,但没有经过顶点,不正确;
D.高没有垂直于底边且没有经过顶点,不正确。
底边对应的高的画法,正确的是选项B。
故答案为:B
3.B
【分析】根据三角形的特性:三角形的两边之和大于第三边,两边之差小于第三边,所以在点B处建桥小南家到小宇家的距离最近。据此解答即可。
【详解】由分析可知,在B处建桥可以使小南家到小宇家的距离最近。
故答案为:B
4.B
【分析】根据观察三个选项,只有B符合三角形的特性,任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【详解】根据三角形的特性:任意两边之和大于第三边,任意两边之差小于第三边,只有B符合。
故答案为:B
【点睛】解答本体的关键根据三角形的特性分析、解答。
5.C
【分析】根据三角形两边之和大于第三边,两边之差小于第三边。以此答题即可。
【详解】根据分析可知:
83=5(dm)
8+3=11(dm)
那么这个三角形的第三条边大于5dm,小于11dm。
3<5=5<8<11=11
一个三角形两条边的长度分别是3dm、8dm,第三条边的长度可能是8dm。
故答案为:C
6.D
【分析】由三条边首尾依次连接组成的封闭图形是三角形。依次数出小三角形的个数,再数出组合的个数,解答即可。
【详解】单独的小三角形,有3个;由2个小三角形组成的三角形,有2个;由3个小三角形组成的三角形,有1个。
3+2+1=6(个)
一共有6个三角形。
故答案为:D
7.B
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此解答即可。
【详解】6+9=15(cm)
9-6=3(cm)
第三条边的长度应比15cm短,比3cm长。
A.2cm<3cm;
B.3cm <4cm<15cm;
C.15cm=15cm;
D.17cm>15cm;
这个三角形的第三条边可能是4cm。
故答案为:B
8. 1 无数 大小 形状 稳定性 变化 变化
【详解】用3根同样大小的小棒围三角形,只能摆出1种三角形;用4根同样大小的小棒围四边形,可以摆出无数种四边形。
我发现:三角形的三条边确定后,它的大小和形状都不会变化,所以三角形具有稳定性。
四边形是不稳定的,它的角度发生了变化,使得形状会随之变化。房屋梁做成三角形、摄影师用的三角支架、自行车的三角架都利用了三角形的稳定性;伸缩门和升降梯则是利用了四边形的不稳定性。
9.3cm/3厘米
【分析】连续的自然数之间,前一个数比后一个数少1,三角形的三边之和为三角形的周长,用12除以3,计算出三条边中间长度的边长是多少,再分别减1和加1,即可算出这另外两条边的长度分别是多少。据此解答。
【详解】12÷3=4(cm)
4-1=3(cm)
4+1=5(cm)
3<4<5
已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为3cm。
10. 大于 小于
【详解】三角形三条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边;
所以,三角形的三边关系两边之和大于第三边;两边之差小于第三边。
11. ② 线段
【分析】直线上任意两点之间的一段叫做线段。连接两点的线段的长度叫做两点间的距离。两点之间,线段最短;据此即可解答。
【详解】根据分析可知,明明从家去学校走第②条路最近,因为两点之间,线段最短。
【点睛】本题主要考查学生对线段特点的掌握和灵活运用。
12.6
【分析】先数单个三角形的,再数两个组合的,再数多个组合的,最后相加即可解答。
【详解】单个:2个
两个组合:3个
多个组合:1个
2+3+1
=5+1
=6(个)
即题图中有6个三角形。
13.①√;②√;③
(1)大于第三边
(2)较短
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边;较短的两根小棒长度和大于最长的小棒,这三根小棒就能摆成三角形;据此即可解答。
【详解】①5+6>13,可以摆成三角形。
( √ )
②5+5>5,可以摆成三角形。
( √ )
③4+4<10,不能摆成三角形。
( )
(1)三角形任意两边之和大于第三边。
(2)最快的方法判断:只要看较短两根的长度和是否大于第三边的长度。
【点睛】熟练掌握三角形三边之间的关系是解答本题的关键。
14. ② 三角形
【分析】根据三角形具有稳定性,解答此题即可。
【详解】根据分析可知,
②不容易变形,因为三角形具有稳定性。
【点睛】熟练掌握三角形的特性,是解答此题的关键。
15. 11 1
【分析】根据三角形三边关系:任意两边之和大于第三边,要使另一根小棒最长,则这根小棒的长度应比两根6厘米长的小棒长度和小1厘米,即(6+6-1)厘米;要使另一根小棒最短,则最长的边为6厘米,则这根小棒的长度加上6厘米的和应比6厘米至少大1厘米,即这根小棒的长度为(6+1-6)厘米;据此解答。
【详解】6+6-1
=12-1
=11(厘米)
6+1-6
=7-6
=1(厘米)
所以,用两根6厘米长的小棒和另一个小棒围成一个三角形(三条边的长都是整厘米数),另一根小棒最长是11厘米,最短是1厘米。
16.A
【分析】三角形的三边关系:三角形任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此即可选择。
【详解】A处是5厘米,第一次在4厘米处剪了一刀,如果第二次剪A处,第二条边长为:,,三角形边的长度之和等于第三边;所以不能剪在A处。
17.×
【分析】在三角形中,任意的两边之和大于第三边,任意的两边之差小于第三边,先判断求出等腰三角形的腰长和底,再求出三角形的周长,据此解答。
【详解】当等腰三角形的腰等于5厘米时,5+5=10,不符合三角形的三边关系,所以三角形的腰等于10厘米,底等于5厘米,因此三角形的周长:10+10+5=25(厘米),周长不可能是20厘米,所以题目说法错误。
故答案为:×
18.√
【分析】三角形具有稳定性,生活中很多设计都是利用这一特性,如:自行车的车架是三角形的,篮球架上篮板的支架是三角形的,电线杆的支架是三角形的,上述物体中的三角形都能使物体更加稳固。
【详解】据分析可得:
小李家里的木桌子松动了,按上图的方法处理比较牢固,是利用了三角形具有稳定性的特性,故此说法正确。
故答案为:√
19.×
【分析】三条线段要想围成三角形,就得满足:三角形任意两边之和大于第三边,任意两边之差小于第三边,据此解答。
【详解】据分析可知:只有满足任意两条线段的和大于第三条线段的三条线段才能构成三角形。
故答案为:×
20.×
【分析】根据三角形的任意两边之和大于第三边,三角形两边之差小于第三边。所以并不是任意三条线段能围成一个三角形的,据此解答。
【详解】因为三条线段要组成三角形;
必须任意两条线段之和大于第三条线段,任意两条线段之差小于第三条线段;
比如三条线段分别是2、2、4,2+2=4,这样的三条线段并不能拼成一个三角形。
所以原题的说法错误。
故答案为:×
【点睛】本题考查了三角形的三边关系,是基础题,熟记三边关系是解题的关键。
21.√
【分析】从电线杠上看出有一个三角形,根据三角形的特性:三角形具有稳定性。即可解答本题。
【详解】为了使电线架在电线杆上更稳固,设计电线杆时根据了三角形的稳定性来设计。
故答案为:√
22.×
【分析】根据三角形的特性:两边之和大于第三边,两边之差小于第三边;进行解答即可。
【详解】6+6=12(厘米),不符合三角形的三边关系:任意两边之和大于第三边,所以用6厘米、6厘米、12厘米三根小棒不能围成一个等腰三角形。所以原题说法错误。
故答案为:×
23.√
【分析】根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,据此判断即可。
【详解】3+4=7cm,7cm<8cm,不能围成三角形。
一个三角形的两条边分别是3cm和4cm,第三边的长度不可能是8cm。原题说法正确,
故答案为:√
24.×
【分析】根据三角形的特性、平行四边形的特性,三角形具有稳定性,而平行四边形容易变形;据此判断。
【详解】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点,例如:埃及金字塔、钢轨、三角形框架、起重机、三角形吊臂、屋顶、三角形钢架、钢架桥和埃菲尔铁塔都以三角形形状建造;
平行四边形具有不稳定性,生活中也有广泛应用,例如:活动挂架,伸缩门等;所以原题说法错误。
故答案为:×
【点睛】此题考查的目的是理解掌握三角形、平行四边形的特性及应用。
25.见详解
【分析】因为梯形的一组对边平行,所以要分成一个梯形和一个三角形,就要用原来梯形一组平行的边,作为新梯形的一组对边,再连接梯形的上底一个顶点和下底上的一点(不要作梯形一条腰的平行线),即可得到一个梯形和一个三角形,解答即可。
【详解】画图如下:
【点睛】熟练掌握梯形、三角形的特征,是解答此题的关键。
26.18分米
【分析】三角形三边的关系:任意两边之和大于第三边,任意两边之差小于第三边;据此解答。
【详解】7+12=19(分米),19分米>18分米
12-7=5(分米),5分米<6分米
第三边长度大于6分米小于18分米,最长为18分米
答:第三根铝合金最长是18分米。
【点睛】掌握三角形三边的关系是解答本题的关键。
27.4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、10厘米
【分析】根据任意三角形的两边之和必须大于第三边,两边之差小于第三边,代入数据,即可解题。
【详解】由分析可知:
4+7=11(厘米)
7-4=3(厘米)
因此另一条边大于3厘米小于11厘米,可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、10厘米。
答:另一条边可能是4厘米、5厘米、6厘米、7厘米、8厘米、9厘米、10厘米。
28.3米、4米、5米、6米、7米、8米、9米、10米、11米、12米、13米
【分析】三角形三边之间的关系:三角形两边之和大于第三边,两边之差小于第三边;据此解答。
【详解】6+8=14(米)
8-6=2(米)
因此第三条边大于2米小于14米;又因为第三条边是整米数,所以第三条边可能是3米、4米、5米、6米、7米、8米、9米、10米、11米、12米、13米。
答:这个三角形菜地的第三条边可能是3米、4米、5米、6米、7米、8米、9米、10米、11米、12米、13米。
29.6种
【分析】根据三角形的任意两边之和大于第三边进行判断即可。
【详解】最短边是3厘米有以下可能:
3厘米、3厘米、4厘米,3+3=6(厘米),4<6,能构成三角形;
3厘米、3厘米、5厘米,3+3=6(厘米),5<6,能构成三角形;
3厘米、4厘米、5厘米,3+4=7(厘米),5<7,能构成三角形;
3厘米、5厘米、5厘米,3+5=8(厘米),5<8,能构成三角形。
最短边是4厘米有以下可能:
4厘米、5厘米、5厘米,4+5=9(厘米),5<9,能构成三角形。
最短边是5厘米有以下可能:
5厘米、5厘米、5厘米,5+5=10(厘米),5<10,能构成三角形。
4+1+1=6(种)
答:能围出6种三角形。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
