湖北省郧西县2024—2025学年下学期期末学业水平监测七年级数学试题(含答案)
文档属性
| 名称 | 湖北省郧西县2024—2025学年下学期期末学业水平监测七年级数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-04 22:20:31 | ||
图片预览



文档简介
郧西县2024—2025学年(下)期末学业水平监测
七年级数学试题
一、选择题(共10小题,每小题3分,共30分)
下列各题有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
1.9的算术平方根是( )
A.±3 B.﹣3 C.3 D.9
2.以下调查中,适合进行抽样调查的是( )
A.火箭发射前对重要零部件的检查 B.调查全班同学每周体育锻炼时间
C.了解某批次节能灯的使用寿命 D.乘坐飞机前,对乘客进行安全检查
3.一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集是( )
A.﹣3≤x<8 B.x<﹣3
C.x≤8 D.﹣3<x≤8
4.若a>b,则下列式子一定成立的是( )
A.a+2<b+2 B.﹣4a>﹣4b C. D.a2>b2
5.如图,下列条件中能判断∠3=∠C的是( )
A.∠1=∠2 B.∠1=∠B
C.∠EDB+∠2=180° D.∠3=∠2
6.若是关于x,y的二元一次方程ax+y=2的解,则a的值是( )
A.﹣1 B.1 C.2 D.﹣2
7.在平面直角坐标系中,点A(﹣3,2),B(3,4),过点A作直线l∥x轴,点C是直线l上的一个动点,当线段BC长度最小时,点C的坐标是( )
A.(﹣3,4) B.(3,2) C.(3,0) D.(4,2)
8.如图,直线AB∥CD,GE⊥EF于点E.若∠BGE=60°,则∠EFD的度数是( )
A.30° B.40°
C.60° D.70°
9.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B. C. D.
10.如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2025次相遇地点的坐标是
A.(1,﹣1) B.(﹣1,1) C.(﹣1,﹣1) D.(2,0)
二、填空题(每小题3分,共15分.请直接将答案填写在答题卡中,不写过程)
11.化简: .
12.在画频数分布直方图时,一组数据的最小值为149,最大值为172,若确定组距为3,则分成的组数是 .
13.如图,有一条平直的等宽纸带按图折叠时,则图中∠α= °.
14.已知关于x的不等式组 的整数解共有4个,则a的取值范围是__________.
15.甲、乙、丙三人共解100道数学题,每人都只会做其中的60道题,且三人合在一起,这100道都能解答出来.将其中只有一人会做的题目叫难题,三人都会做的题叫容易题,则难题比容易题多 .
三、解答题(本题有9个小题,共75分)
16.(8分)(1)计算:;
(2)解方程组:.
17.(6分)求满足不等式组的整数解.
18.(6分)已知:如图,∠1=∠2,∠A=∠E.求证:AD∥BE.
19.(8分)为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间t(单位:分钟),按照完成时间分成五组:A组“t≤45”,B组“45<t≤60”,C组“60<t≤75”,D组“75<t≤90”,E组“t>90”.将收集的数据整理后,绘制成如图所示两幅不完整的统计图.根据以上信息,解答下列问题:
(1)这次调查的样本容量是 ,请补全条形统计图;
(2)在扇形统计图中,B组的圆心角是 度;
(3)若该校有1800名学生,请你估计该校每天完成书面作业不超过90分钟的学生人数.
20.(7分)为表彰在“经典阅读伴成长”读书活动中表现优异的同学,学校计划购进甲、乙两种成套的图书作为活动奖品。已知甲种图书每套60元,乙种图书每套45元,经评选有200名同学在活动中获奖,学校对每位获奖同学奖励1套甲种或乙种图书。如果学校用于购买奖品的资金不超过11500元,那么甲种图书最多能买多少套?
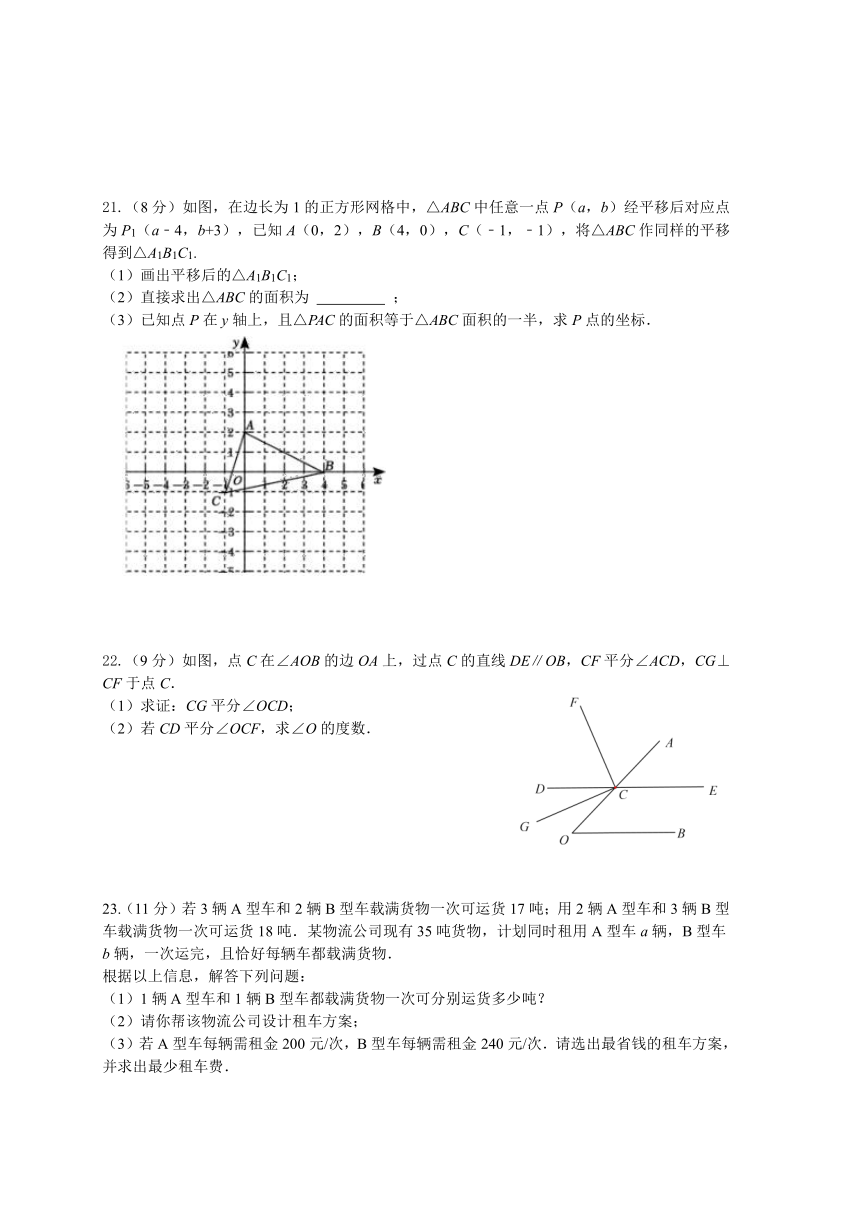
21.(8分)如图,在边长为1的正方形网格中,△ABC中任意一点P(a,b)经平移后对应点为P1(a﹣4,b+3),已知A(0,2),B(4,0),C(﹣1,﹣1),将△ABC作同样的平移得到△A1B1C1.
(1)画出平移后的△A1B1C1;
(2)直接求出△ABC的面积为 ;
(3)已知点P在y轴上,且△PAC的面积等于△ABC面积的一半,求P点的坐标.
22.(9分)如图,点C在∠AOB的边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)求证:CG平分∠OCD;
(2)若CD平分∠OCF,求∠O的度数.
23.(11分)若3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货18吨.某物流公司现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金200元/次,B型车每辆需租金240元/次.请选出最省钱的租车方案,并求出最少租车费.
24.(12分)如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(2,0),且满足
,线段AB交y轴于点F.
(1)填空:a=_______,b=_______;
(2)如图2,点D为y轴正半轴上一点,ED∥AB,且AM,DM分别平分∠CAB,∠ODE,
求∠AMD度数;
(3)如图1,在坐标轴上是否存在点P,使得△ABP的面积与△ABC的面积相等?若存在,求出点P坐标;若不存在,请说明理由.
郧西县2023—2024下学期期末学业水平监测
七年级数学试题参考答案及评分标准
一.选择题:
1---10:CCDC BABA BD
二.填空题:
11. -2 12.8 13.70 14.-2三、解答题:
16.(1)原式=3+3(2)………………………………3分
=3+32
=4;………………………………………………………………4分
(2),
①+②得:9x=18,
解得:x=2,……………………………………………………5分
把x=2代入①得:6+2y=7,
解得:y,……………………………………………………7分
则方程组的解为.…………………………………………8分
17. ,
解不等式①,得:x≤4,…………………………………………1分
解不等式②,得:x,…………………………………………2分
∴该不等式组的解集为x≤4,………………………………4分
∴该不等式组的整数解为1,2,3,4.……………………6分
18.∵ ∠1=∠2 (已知)………………………………………………1分
∴AC//DE (内错角相等,两直线平行)…………………………………2分
∴ ∠3=∠E (两直线平行,内错角相等)…………………………3分
又∠A=∠E(已知)…………………………………………………4分
∴ ∠A =∠3 (等量代换)…………………………………………5分
∴AD∥BE (同位角相等,两直线平行)………………………………6分
19.(1)100;……………………………………………………………………2分
补全的条形统计图如图所示:………………………………………………4分
(2)72;……………………………………………………………………6分
(3)18001710(人),…………………………………………7分
答:估计该校每天完成书面作业不超过90分钟的学生有1710人.………………8分
20.设甲种图书最多能买n套,
则60n+45(200-n)≤11500…………………………………………………………3分
解得 ……………………………………………………………………5分
由n应为正整数,可得n≤166,………………………………………………6分
所以甲种图书最多能买166套。………………………………………………7分
21.(1)由题意知,△ABC是向左平移4个单位长度,向上平移3个单位长度得到的△A1B1C1,
如图,△A1B1C1即为所求.……………………………………………………2分
(2)7,……………………………………………………………………4分
(△ABC的面积为(2+3)×54=7.
故答案为7)
(3)设点P的坐标为(0,m),
∵△PAC的面积等于△ABC面积的一半,
∴,
解得m=9或﹣5,
∴点P的坐标为(0,9)或(0,﹣5).……………………8分
(正确计算出一个点坐标得2分)
22.(1)证明:
∵CG⊥CF,
∴∠FCG=90°,
∴∠ACF+∠OCG=90°,
又∵CF平分∠ACD,
∴∠ACF=∠FCD
∴∠ACF+∠DCG=90°,
而∠FCD+∠DCG=90°,
∴∠DCG=∠OCG,
∴CG平分∠OCD.…………………………………………………………4分
(2)CF平分∠ACD,
∴∠ACF=∠FCD,
又CD平分∠OCF
∠FCD=∠OCD,
∴∠ACF=∠DCF=∠OCD,
∠ACF+∠DCF+∠OCD=180°,
∴∠ACF=∠DCF=∠OCD=60°
DE∥OB
∴∠O=∠OCD=60°,………………………………………………9分
23. (1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,
依题意列方程组得:
,………………………………………………………………2分
解方程组,得:,
答:1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.
……………………………………………………………3分
(2)结合题意和(1)得:3a+4b=35,……………………………………………………4分
∴
∵a,,b都是正整数
∴或或.………………………………………………………6分
答:有3种租车方案:
方案一:A型车1辆,B型车8辆;
方案二:A型车5辆,B型车5辆;
方案三:A型车9辆,B型车2辆.…………………………………………8分
(3)∵A型车每辆需租金200元/次,B型车每辆需租金240元/次,
∴方案一需租金:1×200+8×240=2120(元)
方案二需租金:5×200+5×240=2200(元)
方案三需租金:9×200+2×240=2280(元)………………………………………10分
∵2280>2200>2120,
∴最省钱的租车方案是方案一:A型车1辆,B型车8辆,最少租车费为2120元.
………………………………………11分
24.(12分) 解:(1) a=–3, b=3;…………………………………2分
(2)设∠BAM=∠CAM=,∠ODM=∠EDM=β
由三角形内角和等于180 ,得
∠PAO+∠APO+∠AOP=∠DPM+∠PDM+∠M=180
即+90 =β+∠M
∴∠M=90 +-β……………………………………………………4分
∵ED∥AB
∴∠EDF=∠AFD
即2β=2+90
∴β-=45 ……………………………………………………………6分
∴∠M=90 +-β=45 …………………………………………………………………7分
(3)存在符合要求的点P.
①当点P在x轴上时,过点B作BG⊥x轴于点G.
由S△ABP=S△ABC 得AP·BG=AC·BG
∴AP=AC=5……………………………………………………8分
∴P1(2,0),P2(–8,0); ………………………………9分
②当点P在y 轴上时,将△AFO沿x轴向右平移,使点A与点O重合,
得△OF'O',则点B在O'F'的延长线上,四边形OFBF'是平行四边形.
∴OF=BF'=O'F'=BO'=………………………………10分
过点B作BH⊥y轴于点H.
由S△ABP=S△APF+S△BPF=S△ABC得
PF·AO+PF·BH=AC·BO'
即3PF+3PF=15
∴PF=………………………………………………………11分
∴P3(0,4),P4(0,–1)
综上,符合要求的点P坐标分别为P1(2,0),P2(–8,0),P3(0,4),P4(0,–1) ………12分
【说明】本题用其它方法,只要过程完整,均可酌情给分.
七年级数学试题
一、选择题(共10小题,每小题3分,共30分)
下列各题有且只有一个正确答案,请在答题卡上将正确答案的标号涂黑.
1.9的算术平方根是( )
A.±3 B.﹣3 C.3 D.9
2.以下调查中,适合进行抽样调查的是( )
A.火箭发射前对重要零部件的检查 B.调查全班同学每周体育锻炼时间
C.了解某批次节能灯的使用寿命 D.乘坐飞机前,对乘客进行安全检查
3.一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集是( )
A.﹣3≤x<8 B.x<﹣3
C.x≤8 D.﹣3<x≤8
4.若a>b,则下列式子一定成立的是( )
A.a+2<b+2 B.﹣4a>﹣4b C. D.a2>b2
5.如图,下列条件中能判断∠3=∠C的是( )
A.∠1=∠2 B.∠1=∠B
C.∠EDB+∠2=180° D.∠3=∠2
6.若是关于x,y的二元一次方程ax+y=2的解,则a的值是( )
A.﹣1 B.1 C.2 D.﹣2
7.在平面直角坐标系中,点A(﹣3,2),B(3,4),过点A作直线l∥x轴,点C是直线l上的一个动点,当线段BC长度最小时,点C的坐标是( )
A.(﹣3,4) B.(3,2) C.(3,0) D.(4,2)
8.如图,直线AB∥CD,GE⊥EF于点E.若∠BGE=60°,则∠EFD的度数是( )
A.30° B.40°
C.60° D.70°
9.《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有x人,y辆车,可列方程组为( )
A. B. C. D.
10.如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2025次相遇地点的坐标是
A.(1,﹣1) B.(﹣1,1) C.(﹣1,﹣1) D.(2,0)
二、填空题(每小题3分,共15分.请直接将答案填写在答题卡中,不写过程)
11.化简: .
12.在画频数分布直方图时,一组数据的最小值为149,最大值为172,若确定组距为3,则分成的组数是 .
13.如图,有一条平直的等宽纸带按图折叠时,则图中∠α= °.
14.已知关于x的不等式组 的整数解共有4个,则a的取值范围是__________.
15.甲、乙、丙三人共解100道数学题,每人都只会做其中的60道题,且三人合在一起,这100道都能解答出来.将其中只有一人会做的题目叫难题,三人都会做的题叫容易题,则难题比容易题多 .
三、解答题(本题有9个小题,共75分)
16.(8分)(1)计算:;
(2)解方程组:.
17.(6分)求满足不等式组的整数解.
18.(6分)已知:如图,∠1=∠2,∠A=∠E.求证:AD∥BE.
19.(8分)为落实“双减”政策,优化作业管理,某中学从全体学生中随机抽取部分学生,调查他们每天完成书面作业的时间t(单位:分钟),按照完成时间分成五组:A组“t≤45”,B组“45<t≤60”,C组“60<t≤75”,D组“75<t≤90”,E组“t>90”.将收集的数据整理后,绘制成如图所示两幅不完整的统计图.根据以上信息,解答下列问题:
(1)这次调查的样本容量是 ,请补全条形统计图;
(2)在扇形统计图中,B组的圆心角是 度;
(3)若该校有1800名学生,请你估计该校每天完成书面作业不超过90分钟的学生人数.
20.(7分)为表彰在“经典阅读伴成长”读书活动中表现优异的同学,学校计划购进甲、乙两种成套的图书作为活动奖品。已知甲种图书每套60元,乙种图书每套45元,经评选有200名同学在活动中获奖,学校对每位获奖同学奖励1套甲种或乙种图书。如果学校用于购买奖品的资金不超过11500元,那么甲种图书最多能买多少套?
21.(8分)如图,在边长为1的正方形网格中,△ABC中任意一点P(a,b)经平移后对应点为P1(a﹣4,b+3),已知A(0,2),B(4,0),C(﹣1,﹣1),将△ABC作同样的平移得到△A1B1C1.
(1)画出平移后的△A1B1C1;
(2)直接求出△ABC的面积为 ;
(3)已知点P在y轴上,且△PAC的面积等于△ABC面积的一半,求P点的坐标.
22.(9分)如图,点C在∠AOB的边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)求证:CG平分∠OCD;
(2)若CD平分∠OCF,求∠O的度数.
23.(11分)若3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货18吨.某物流公司现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金200元/次,B型车每辆需租金240元/次.请选出最省钱的租车方案,并求出最少租车费.
24.(12分)如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(2,0),且满足
,线段AB交y轴于点F.
(1)填空:a=_______,b=_______;
(2)如图2,点D为y轴正半轴上一点,ED∥AB,且AM,DM分别平分∠CAB,∠ODE,
求∠AMD度数;
(3)如图1,在坐标轴上是否存在点P,使得△ABP的面积与△ABC的面积相等?若存在,求出点P坐标;若不存在,请说明理由.
郧西县2023—2024下学期期末学业水平监测
七年级数学试题参考答案及评分标准
一.选择题:
1---10:CCDC BABA BD
二.填空题:
11. -2 12.8 13.70 14.-2
16.(1)原式=3+3(2)………………………………3分
=3+32
=4;………………………………………………………………4分
(2),
①+②得:9x=18,
解得:x=2,……………………………………………………5分
把x=2代入①得:6+2y=7,
解得:y,……………………………………………………7分
则方程组的解为.…………………………………………8分
17. ,
解不等式①,得:x≤4,…………………………………………1分
解不等式②,得:x,…………………………………………2分
∴该不等式组的解集为x≤4,………………………………4分
∴该不等式组的整数解为1,2,3,4.……………………6分
18.∵ ∠1=∠2 (已知)………………………………………………1分
∴AC//DE (内错角相等,两直线平行)…………………………………2分
∴ ∠3=∠E (两直线平行,内错角相等)…………………………3分
又∠A=∠E(已知)…………………………………………………4分
∴ ∠A =∠3 (等量代换)…………………………………………5分
∴AD∥BE (同位角相等,两直线平行)………………………………6分
19.(1)100;……………………………………………………………………2分
补全的条形统计图如图所示:………………………………………………4分
(2)72;……………………………………………………………………6分
(3)18001710(人),…………………………………………7分
答:估计该校每天完成书面作业不超过90分钟的学生有1710人.………………8分
20.设甲种图书最多能买n套,
则60n+45(200-n)≤11500…………………………………………………………3分
解得 ……………………………………………………………………5分
由n应为正整数,可得n≤166,………………………………………………6分
所以甲种图书最多能买166套。………………………………………………7分
21.(1)由题意知,△ABC是向左平移4个单位长度,向上平移3个单位长度得到的△A1B1C1,
如图,△A1B1C1即为所求.……………………………………………………2分
(2)7,……………………………………………………………………4分
(△ABC的面积为(2+3)×54=7.
故答案为7)
(3)设点P的坐标为(0,m),
∵△PAC的面积等于△ABC面积的一半,
∴,
解得m=9或﹣5,
∴点P的坐标为(0,9)或(0,﹣5).……………………8分
(正确计算出一个点坐标得2分)
22.(1)证明:
∵CG⊥CF,
∴∠FCG=90°,
∴∠ACF+∠OCG=90°,
又∵CF平分∠ACD,
∴∠ACF=∠FCD
∴∠ACF+∠DCG=90°,
而∠FCD+∠DCG=90°,
∴∠DCG=∠OCG,
∴CG平分∠OCD.…………………………………………………………4分
(2)CF平分∠ACD,
∴∠ACF=∠FCD,
又CD平分∠OCF
∠FCD=∠OCD,
∴∠ACF=∠DCF=∠OCD,
∠ACF+∠DCF+∠OCD=180°,
∴∠ACF=∠DCF=∠OCD=60°
DE∥OB
∴∠O=∠OCD=60°,………………………………………………9分
23. (1)设每辆A型车、B型车都装满货物一次可以分别运货x吨、y吨,
依题意列方程组得:
,………………………………………………………………2分
解方程组,得:,
答:1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨.
……………………………………………………………3分
(2)结合题意和(1)得:3a+4b=35,……………………………………………………4分
∴
∵a,,b都是正整数
∴或或.………………………………………………………6分
答:有3种租车方案:
方案一:A型车1辆,B型车8辆;
方案二:A型车5辆,B型车5辆;
方案三:A型车9辆,B型车2辆.…………………………………………8分
(3)∵A型车每辆需租金200元/次,B型车每辆需租金240元/次,
∴方案一需租金:1×200+8×240=2120(元)
方案二需租金:5×200+5×240=2200(元)
方案三需租金:9×200+2×240=2280(元)………………………………………10分
∵2280>2200>2120,
∴最省钱的租车方案是方案一:A型车1辆,B型车8辆,最少租车费为2120元.
………………………………………11分
24.(12分) 解:(1) a=–3, b=3;…………………………………2分
(2)设∠BAM=∠CAM=,∠ODM=∠EDM=β
由三角形内角和等于180 ,得
∠PAO+∠APO+∠AOP=∠DPM+∠PDM+∠M=180
即+90 =β+∠M
∴∠M=90 +-β……………………………………………………4分
∵ED∥AB
∴∠EDF=∠AFD
即2β=2+90
∴β-=45 ……………………………………………………………6分
∴∠M=90 +-β=45 …………………………………………………………………7分
(3)存在符合要求的点P.
①当点P在x轴上时,过点B作BG⊥x轴于点G.
由S△ABP=S△ABC 得AP·BG=AC·BG
∴AP=AC=5……………………………………………………8分
∴P1(2,0),P2(–8,0); ………………………………9分
②当点P在y 轴上时,将△AFO沿x轴向右平移,使点A与点O重合,
得△OF'O',则点B在O'F'的延长线上,四边形OFBF'是平行四边形.
∴OF=BF'=O'F'=BO'=………………………………10分
过点B作BH⊥y轴于点H.
由S△ABP=S△APF+S△BPF=S△ABC得
PF·AO+PF·BH=AC·BO'
即3PF+3PF=15
∴PF=………………………………………………………11分
∴P3(0,4),P4(0,–1)
综上,符合要求的点P坐标分别为P1(2,0),P2(–8,0),P3(0,4),P4(0,–1) ………12分
【说明】本题用其它方法,只要过程完整,均可酌情给分.
同课章节目录
