1.1 第2课时 验证勾股定理及其简单应用 课件(共27张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 1.1 第2课时 验证勾股定理及其简单应用 课件(共27张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
第2课时 验证勾股定理及其简单应用
第 一 章 勾股定理
1.探索勾股定理
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
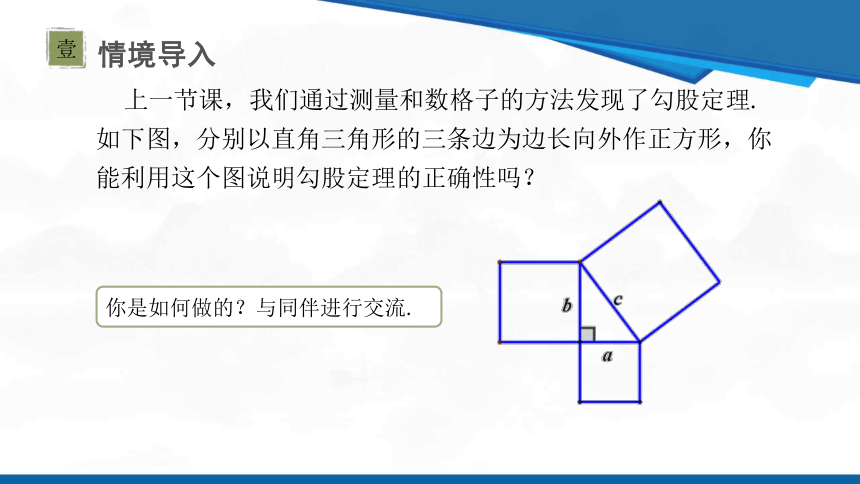
你是如何做的?与同伴进行交流.
上一节课,我们通过测量和数格子的方法发现了勾股定理.如下图,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?
新知初探
贰
新知初探
探究一:勾股定理的验证
贰
据不完全统计,验证的方法有500多种,你有自己的方法吗?
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢 ?
新知初探
贰
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
新知初探
贰
c
a
b
c
a
b
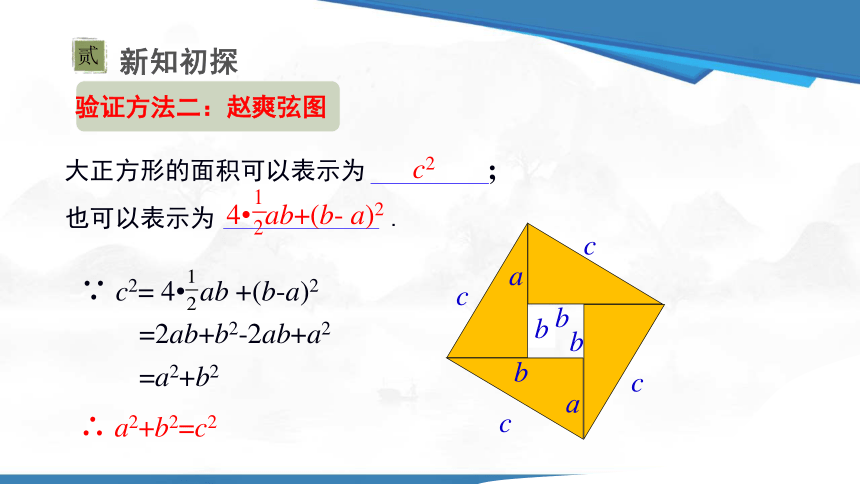
验证方法二:赵爽弦图
b
c
a
b
c
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4 ab+(b- a)2
新知初探
贰
b
c
a
b
c
a
A
B
C
D
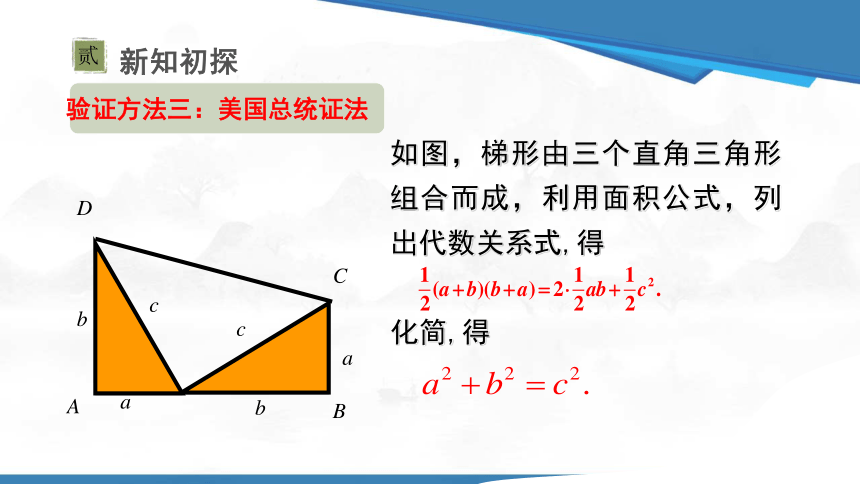
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
验证方法三:美国总统证法
新知初探
贰
a
b
c
青入
青方
青
出
青出
青入
朱入
朱方
朱出
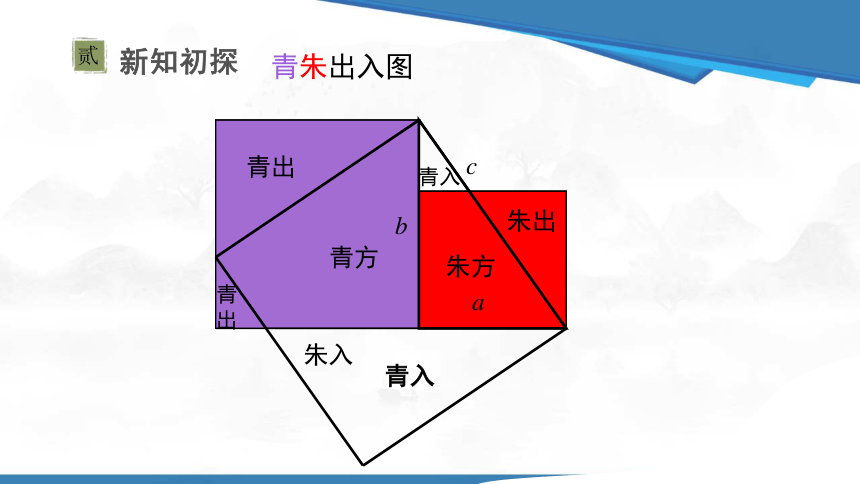
青朱出入图
新知初探
贰
a
b
c
A
B
C
D
E
F
O
达·芬奇对勾股定理的证明
新知初探
贰
新知初探
贰
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
新知初探
贰
如图,过 A 点画一直线 AL 使其垂直于 DE, 并交 DE 于 L,交 BC 于 M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与 矩形MLEC也等积,于是推得
欧几里得证明勾股定理
新知初探
探究二:勾股定理简单应用
贰
例:在一次军事演习中,红方侦查员王叔叔在距离东西向公路400m处侦查,发现一辆蓝方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算蓝方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,得AB2=BC2+AC2,
即 5002=BC2+4002,
所以,BC=300.
蓝方汽车10s行驶了300m,那么它1s行驶的距离为300÷10=30(m)
即蓝方汽车行驶的速度为30m/s.
新知初探
贰
1.如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少走( )
A.140米 B.120米 C.100米 D.90米
随堂练习
C
新知初探
贰
2.如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别是3,5,2,3,则最大正方形E的面积是( )
A.10 B.13 C.15 D.26
B
新知初探
贰
3.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端到地面的距离2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙上,其顶端距离地面1.5米,那么小巷的宽度为 米。
2
新知初探
贰
4.如图,某人划船横渡一条河,由于水流的影响,实际上岸地点偏离欲到达点25 m,结果他在水中实际划了65 m,求该河流的宽度。
解:根据题中数据,由勾股定理可得,
AB2=AC2-BC2=652-252=3 600,
则AB=60 m。
答:该河流的宽度是60米。
新知初探
贰
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2.说说你的判断和理由,并与同伴进行交流。
当堂达标
叁
当堂达标
叁
1.在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可)
2.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
当堂达标
叁
3.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
解:设旗杆顶部到折断处的距离为x m,
根据勾股定理得
解得x=15, 15+9=24(m).
答:旗杆原来高24 m.
当堂达标
叁
4.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,AD=13m,∠B=∠ACD=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
解:在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2,∴AC=5m,
在Rt△ACD中,由勾股定理,
得 CD2=AD2-AC2,∴CD=12m,
S草坪=SRt△ABC+SRt△ACD= AB BC+ AC DC
= (3×4+5×12)=36 m2.
故需要的费用为36×100=3600元.
课堂小结
肆
课堂小结
肆
探索勾股定理
勾股定理的验证
勾股定理的简单运用
课后作业
基础题:1.随堂练习第 1题。
提高题:2.习题第7、8题。
谢
谢
第2课时 验证勾股定理及其简单应用
第 一 章 勾股定理
1.探索勾股定理
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
你是如何做的?与同伴进行交流.
上一节课,我们通过测量和数格子的方法发现了勾股定理.如下图,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?
新知初探
贰
新知初探
探究一:勾股定理的验证
贰
据不完全统计,验证的方法有500多种,你有自己的方法吗?
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢 ?
新知初探
贰
a
a
a
a
b
b
b
b
c
c
c
c
方法小结:我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
验证方法一:毕达哥拉斯证法
大正方形的面积可以表示为 ;
也可以表示为 .
(a+b)2
c2 +4 ab
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
新知初探
贰
c
a
b
c
a
b
验证方法二:赵爽弦图
b
c
a
b
c
大正方形的面积可以表示为 ;
也可以表示为 .
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∴ a2+b2=c2
c2
4 ab+(b- a)2
新知初探
贰
b
c
a
b
c
a
A
B
C
D
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
验证方法三:美国总统证法
新知初探
贰
a
b
c
青入
青方
青
出
青出
青入
朱入
朱方
朱出
青朱出入图
新知初探
贰
a
b
c
A
B
C
D
E
F
O
达·芬奇对勾股定理的证明
新知初探
贰
新知初探
贰
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
新知初探
贰
如图,过 A 点画一直线 AL 使其垂直于 DE, 并交 DE 于 L,交 BC 于 M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与 矩形MLEC也等积,于是推得
欧几里得证明勾股定理
新知初探
探究二:勾股定理简单应用
贰
例:在一次军事演习中,红方侦查员王叔叔在距离东西向公路400m处侦查,发现一辆蓝方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算蓝方汽车的速度吗
公路
B
C
A
400m
500m
解:由勾股定理,得AB2=BC2+AC2,
即 5002=BC2+4002,
所以,BC=300.
蓝方汽车10s行驶了300m,那么它1s行驶的距离为300÷10=30(m)
即蓝方汽车行驶的速度为30m/s.
新知初探
贰
1.如图是我校的长方形水泥操场,如果一学生要从A角走到C角,至少走( )
A.140米 B.120米 C.100米 D.90米
随堂练习
C
新知初探
贰
2.如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别是3,5,2,3,则最大正方形E的面积是( )
A.10 B.13 C.15 D.26
B
新知初探
贰
3.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端到地面的距离2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙上,其顶端距离地面1.5米,那么小巷的宽度为 米。
2
新知初探
贰
4.如图,某人划船横渡一条河,由于水流的影响,实际上岸地点偏离欲到达点25 m,结果他在水中实际划了65 m,求该河流的宽度。
解:根据题中数据,由勾股定理可得,
AB2=AC2-BC2=652-252=3 600,
则AB=60 m。
答:该河流的宽度是60米。
新知初探
贰
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2.说说你的判断和理由,并与同伴进行交流。
当堂达标
叁
当堂达标
叁
1.在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可)
2.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
当堂达标
叁
3.如图,一根旗杆在离地面9 m处折断,旗杆顶部落在离旗杆底部12 m处.旗杆原来有多高
12 m
9 m
解:设旗杆顶部到折断处的距离为x m,
根据勾股定理得
解得x=15, 15+9=24(m).
答:旗杆原来高24 m.
当堂达标
叁
4.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,AD=13m,∠B=∠ACD=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
解:在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2,∴AC=5m,
在Rt△ACD中,由勾股定理,
得 CD2=AD2-AC2,∴CD=12m,
S草坪=SRt△ABC+SRt△ACD= AB BC+ AC DC
= (3×4+5×12)=36 m2.
故需要的费用为36×100=3600元.
课堂小结
肆
课堂小结
肆
探索勾股定理
勾股定理的验证
勾股定理的简单运用
课后作业
基础题:1.随堂练习第 1题。
提高题:2.习题第7、8题。
谢
谢
同课章节目录
