1.1 第1课时 探索勾股定理 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 1.1 第1课时 探索勾股定理 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:05:54 | ||
图片预览





文档简介
(共24张PPT)
第1课时 探索勾股定理
第 一 章 勾股定理
1.探索勾股定理
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
如图,这是一幅美丽的图案,仔细观察,你能发现这幅图中的奥秘吗?带着疑问我们来一起探索吧.
新知初探
贰
新知初探
探究一:勾股定理的初步认识
贰
(图中每一格代表
一平方厘米)
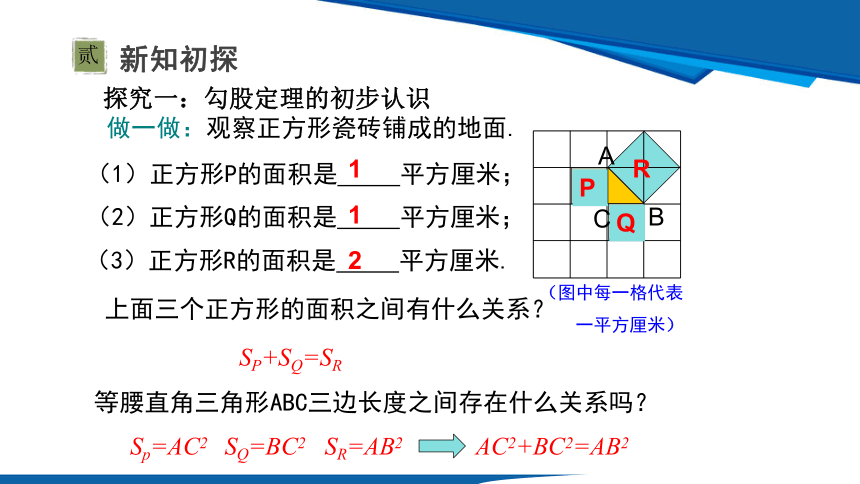
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
做一做:观察正方形瓷砖铺成的地面.
新知初探
贰
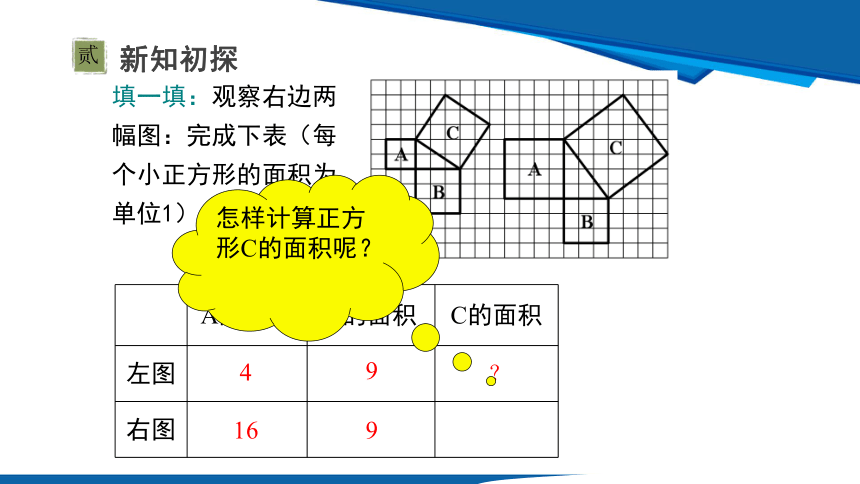
填一填:观察右边两幅图:完成下表(每个小正方形的面积为单位1).
A的面积 B的面积 C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
新知初探
贰
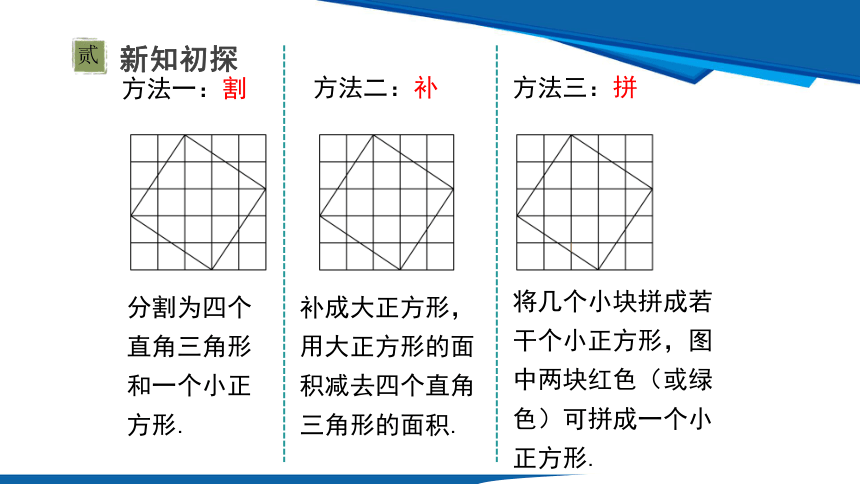
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
新知初探
贰
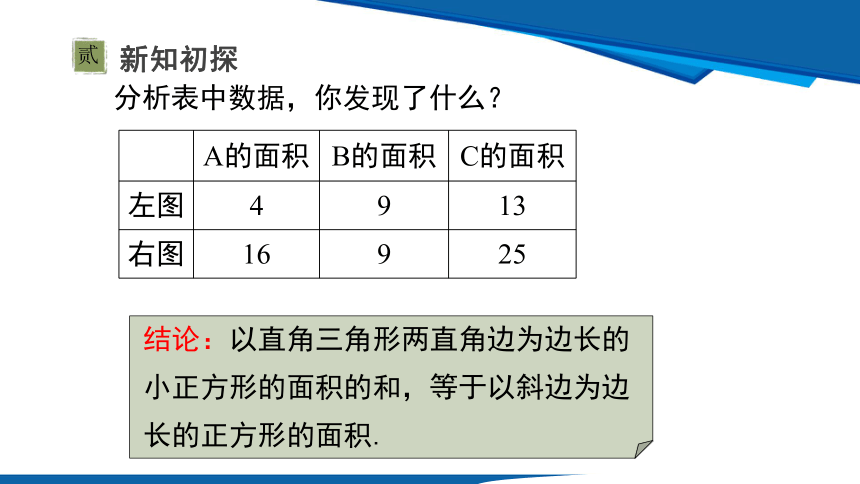
分析表中数据,你发现了什么?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
新知初探
贰
分别以5cm、12cm为直角三角形的直角边作出一个直角三角形ABC,测量斜边的长度,然后验证上述关系对这个直角三角形是否成立.
13
5
12
A
B
C
做一做
新知初探
贰
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
总结归纳
定理揭示了直角三角形三边之间的关系.
直角三角形两直角边的平方和等于斜边的平方.如果a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
勾股定理
新知初探
探究二:初步运用勾股定理求直角三角形的边长
贰
例.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42=0.49,
所以BC=0.7.
答:梯脚与墙的距离是0.7米.
新知初探
贰
1.如图,在△ABC中,∠B=90°,AB=1,BC=2,
四边形ADEC是正方形,则正方形ADEC的面积是( )
A.3 B.4 C.5 D.6
随堂练习
C
新知初探
贰
2.如图,点C是线段AB上的一点分别以AC,BC为边向两侧作正方形。设AB=6,两个正方形的面积和S1+S2=20,则图中△BCD的面积为( )
A.4 B.6 C.8 D.10
A
新知初探
贰
3.求下图中字母所代表的正方形面积。
解:SA=16+9=25;SB=169-25=144。
新知初探
贰
4.求出下列直角三角形中未知边的长度。
解:x2=152+202=625,x=25;
y2=132-52=144,y=12。
当堂达标
叁
当堂达标
叁
1.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
当堂达标
叁
2. 求下列图中未知数x、y的值:
解:由勾股定理可得:
81+ 144=x2
即:x2=225
x=15
解:由勾股定理可得:
y2+ 144=169
即:y2=25
y=5
当堂达标
叁
3.在△ABC中,∠C=90°.
(1)若a=6,b=8,则c= .
(2)若c=13,b=12,则a= .
4.若直角三角形中,有两边长是3和4,则第三
边长的平方为( )
A 25 B 14 C 7 D 7或25
10
5
D
当堂达标
叁
5.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
所以 x=±8(负值舍去),
所以另一直角边长为8 cm,
直角三角形的面积是:
(cm2).
课堂小结
肆
课堂小结
肆
认识勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
课后作业
基础题:1.课堂练习 第 1、2题,习题1.1第1、2、3。
提高题:习题1.1第4、6
谢
谢
第1课时 探索勾股定理
第 一 章 勾股定理
1.探索勾股定理
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
如图,这是一幅美丽的图案,仔细观察,你能发现这幅图中的奥秘吗?带着疑问我们来一起探索吧.
新知初探
贰
新知初探
探究一:勾股定理的初步认识
贰
(图中每一格代表
一平方厘米)
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
做一做:观察正方形瓷砖铺成的地面.
新知初探
贰
填一填:观察右边两幅图:完成下表(每个小正方形的面积为单位1).
A的面积 B的面积 C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
新知初探
贰
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
新知初探
贰
分析表中数据,你发现了什么?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
新知初探
贰
分别以5cm、12cm为直角三角形的直角边作出一个直角三角形ABC,测量斜边的长度,然后验证上述关系对这个直角三角形是否成立.
13
5
12
A
B
C
做一做
新知初探
贰
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
总结归纳
定理揭示了直角三角形三边之间的关系.
直角三角形两直角边的平方和等于斜边的平方.如果a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
勾股定理
新知初探
探究二:初步运用勾股定理求直角三角形的边长
贰
例.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42=0.49,
所以BC=0.7.
答:梯脚与墙的距离是0.7米.
新知初探
贰
1.如图,在△ABC中,∠B=90°,AB=1,BC=2,
四边形ADEC是正方形,则正方形ADEC的面积是( )
A.3 B.4 C.5 D.6
随堂练习
C
新知初探
贰
2.如图,点C是线段AB上的一点分别以AC,BC为边向两侧作正方形。设AB=6,两个正方形的面积和S1+S2=20,则图中△BCD的面积为( )
A.4 B.6 C.8 D.10
A
新知初探
贰
3.求下图中字母所代表的正方形面积。
解:SA=16+9=25;SB=169-25=144。
新知初探
贰
4.求出下列直角三角形中未知边的长度。
解:x2=152+202=625,x=25;
y2=132-52=144,y=12。
当堂达标
叁
当堂达标
叁
1.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
当堂达标
叁
2. 求下列图中未知数x、y的值:
解:由勾股定理可得:
81+ 144=x2
即:x2=225
x=15
解:由勾股定理可得:
y2+ 144=169
即:y2=25
y=5
当堂达标
叁
3.在△ABC中,∠C=90°.
(1)若a=6,b=8,则c= .
(2)若c=13,b=12,则a= .
4.若直角三角形中,有两边长是3和4,则第三
边长的平方为( )
A 25 B 14 C 7 D 7或25
10
5
D
当堂达标
叁
5.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.
由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
所以 x=±8(负值舍去),
所以另一直角边长为8 cm,
直角三角形的面积是:
(cm2).
课堂小结
肆
课堂小结
肆
认识勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
课后作业
基础题:1.课堂练习 第 1、2题,习题1.1第1、2、3。
提高题:习题1.1第4、6
谢
谢
同课章节目录
