1.2 一定是直角三角形吗 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 1.2 一定是直角三角形吗 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:19:11 | ||
图片预览






文档简介
(共23张PPT)
第一章 勾股定理
2 一定是直角三角形吗
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
问题:同学们你们知道古埃及人用什么方法得到直角的吗
用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第9个结,拉紧绳子就得到一个直角三角形, 其直角在第1个结处.
新知初探
贰
新知初探
探究一:探究勾股定理的逆定理
贰
探究:下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
回答下列问题:
1.这三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
新知初探
贰
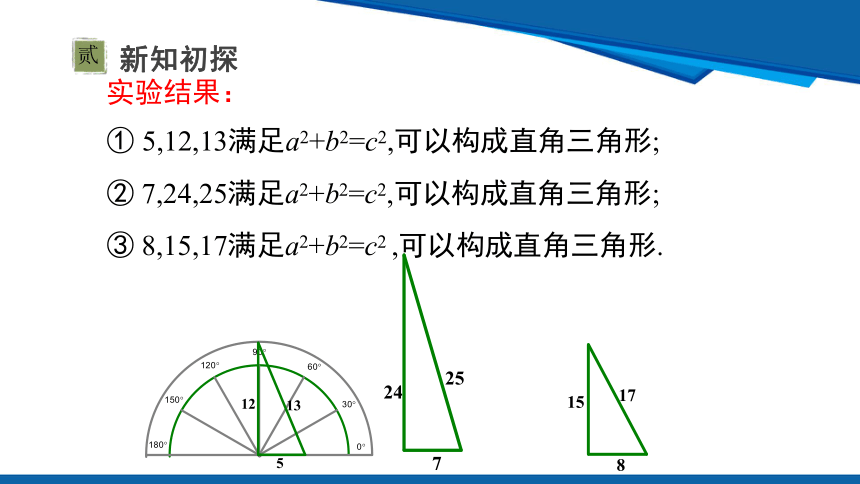
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
新知初探
贰
思考:从上述问题中,能发现什么结论吗?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
有同学认为测量结果可能有误差,不同意
这个发现.你觉得这个发现正确吗 你能给
出一个更有说服力的理由吗
新知初探
贰
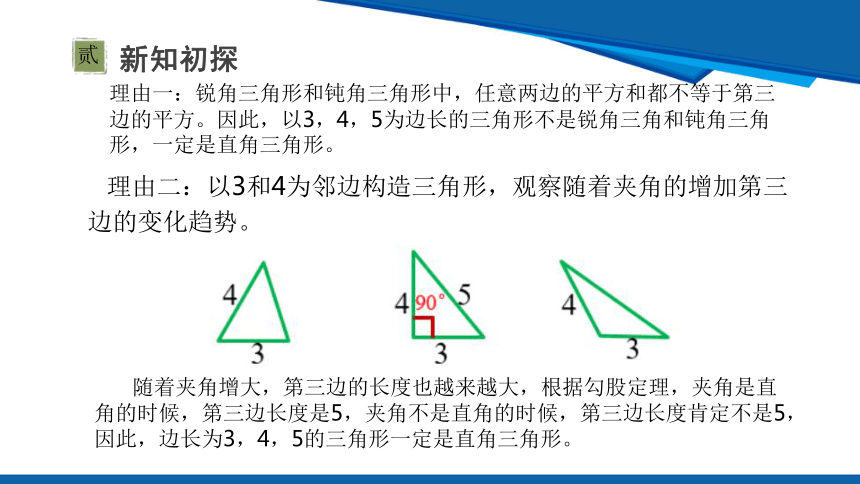
理由一:锐角三角形和钝角三角形中,任意两边的平方和都不等于第三边的平方。因此,以3,4,5为边长的三角形不是锐角三角和钝角三角形,一定是直角三角形。
理由二:以3和4为邻边构造三角形,观察随着夹角的增加第三边的变化趋势。
随着夹角增大,第三边的长度也越来越大,根据勾股定理,夹角是直角的时候,第三边长度是5,夹角不是直角的时候,第三边长度肯定不是5,因此,边长为3,4,5的三角形一定是直角三角形。
新知初探
贰
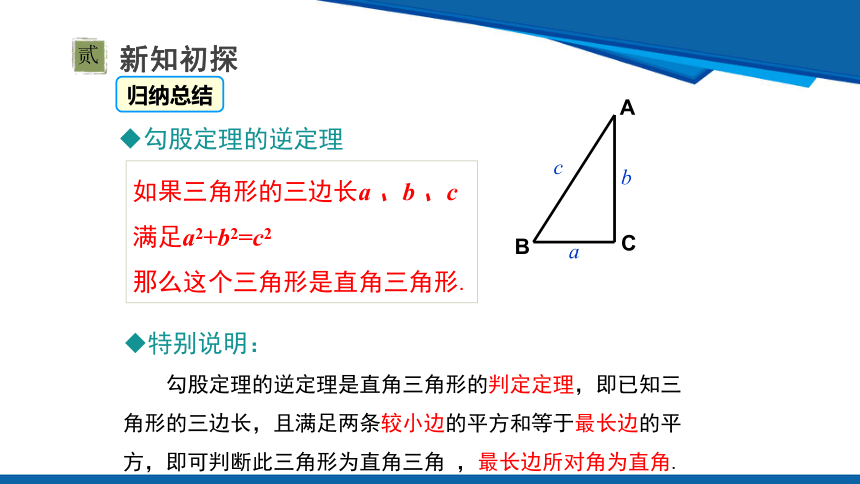
勾股定理的逆定理
归纳总结
如果三角形的三边长a 、b 、c
满足a2+b2=c2
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角 ,最长边所对角为直角.
特别说明:
新知初探
贰
如果三角形的三边长a,b,c满足a2+b2=c
那么这个三角形是直角三角形.
满足a2+b2=c2的三个正整数,称为勾股数.
概念学习
新知初探
贰
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数k,得到一组新数,这组数同样是勾股数.
新知初探
探究二:勾股定理逆定理的应用
贰
例:一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
新知初探
贰
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
新知初探
贰
1.木工师傅想利用木条制作一个直角三角形,那么下列各组数据不符合直角三角形的三边长的是( )
A.3,4,5 B.6,8,10
C.5,12,13 D.7,15,17
2.下列各组数中,为勾股数的是( )
A.0.6,0.8,1 B.2,3,4
D
D
3.若三角形的三边长满足|c2-a2-b2|+(a-b)2=0,则此三角形的形状是 。
等腰直角三角形
随堂练习
新知初探
贰
4.一艘在海上朝正北方向航行的轮船,航行240海里时方位仪坏了,凭经验,船长指挥船左转90°,继续航行70海里,则距出发地250海里,你能判断船转弯后,是否沿正西方向航行?
解:由题意画出相应的图形,如图。
当堂达标
叁
当堂达标
叁
1.如果线段a,b,c能组成直角三角形,则它们的比可以是 ( )
A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
将直角三角形的三边长扩大同样的倍数,则得到
的三角形 ( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
B
A
叁
当堂达标
叁
4.如果三条线段a,b,c满足a2=c2-b2,这三条线段组成的三角形是直角三角形吗 为什么
解:是直角三角形.因为a2+b2=c2满足勾股定理的逆定理.
3.以△ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
直角
叁
当堂达标
叁
5.如图,在正方形ABCD中,AB=4,AE=2,DF=1,
图中有几个直角三角形,你是如何判断的?
与你的同伴交流.
4
1
2
2
4
3
解:△ABE,△DEF,△FCB △BEF均为直角三角形.
由勾股定理知
BE2=22+42=20,
EF2=22+12=5,
BF2=32+42=25,
∴BE2+EF2=BF2,
∴ △BEF是直角三角形.
叁
课堂小结
肆
课堂小结
肆
一定是直角三角形吗
勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
勾股数:满足a2+b2=c2的三个正整数
肆
课后作业
基础题:1.随堂练习 第 1,2题;习题1.2第1,2,3题
提高题:2. 习题1.2第3, 5题。
谢
谢
第一章 勾股定理
2 一定是直角三角形吗
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
问题:同学们你们知道古埃及人用什么方法得到直角的吗
用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第9个结,拉紧绳子就得到一个直角三角形, 其直角在第1个结处.
新知初探
贰
新知初探
探究一:探究勾股定理的逆定理
贰
探究:下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
回答下列问题:
1.这三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
新知初探
贰
实验结果:
① 5,12,13满足a2+b2=c2,可以构成直角三角形;
③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
② 7,24,25满足a2+b2=c2,可以构成直角三角形;
新知初探
贰
思考:从上述问题中,能发现什么结论吗?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
有同学认为测量结果可能有误差,不同意
这个发现.你觉得这个发现正确吗 你能给
出一个更有说服力的理由吗
新知初探
贰
理由一:锐角三角形和钝角三角形中,任意两边的平方和都不等于第三边的平方。因此,以3,4,5为边长的三角形不是锐角三角和钝角三角形,一定是直角三角形。
理由二:以3和4为邻边构造三角形,观察随着夹角的增加第三边的变化趋势。
随着夹角增大,第三边的长度也越来越大,根据勾股定理,夹角是直角的时候,第三边长度是5,夹角不是直角的时候,第三边长度肯定不是5,因此,边长为3,4,5的三角形一定是直角三角形。
新知初探
贰
勾股定理的逆定理
归纳总结
如果三角形的三边长a 、b 、c
满足a2+b2=c2
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角 ,最长边所对角为直角.
特别说明:
新知初探
贰
如果三角形的三边长a,b,c满足a2+b2=c
那么这个三角形是直角三角形.
满足a2+b2=c2的三个正整数,称为勾股数.
概念学习
新知初探
贰
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数k,得到一组新数,这组数同样是勾股数.
新知初探
探究二:勾股定理逆定理的应用
贰
例:一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图1
图2
新知初探
贰
在△BCD中,
所以△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
所以△ABD 是直角三角形,∠A是直角.
新知初探
贰
1.木工师傅想利用木条制作一个直角三角形,那么下列各组数据不符合直角三角形的三边长的是( )
A.3,4,5 B.6,8,10
C.5,12,13 D.7,15,17
2.下列各组数中,为勾股数的是( )
A.0.6,0.8,1 B.2,3,4
D
D
3.若三角形的三边长满足|c2-a2-b2|+(a-b)2=0,则此三角形的形状是 。
等腰直角三角形
随堂练习
新知初探
贰
4.一艘在海上朝正北方向航行的轮船,航行240海里时方位仪坏了,凭经验,船长指挥船左转90°,继续航行70海里,则距出发地250海里,你能判断船转弯后,是否沿正西方向航行?
解:由题意画出相应的图形,如图。
当堂达标
叁
当堂达标
叁
1.如果线段a,b,c能组成直角三角形,则它们的比可以是 ( )
A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
将直角三角形的三边长扩大同样的倍数,则得到
的三角形 ( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
B
A
叁
当堂达标
叁
4.如果三条线段a,b,c满足a2=c2-b2,这三条线段组成的三角形是直角三角形吗 为什么
解:是直角三角形.因为a2+b2=c2满足勾股定理的逆定理.
3.以△ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
直角
叁
当堂达标
叁
5.如图,在正方形ABCD中,AB=4,AE=2,DF=1,
图中有几个直角三角形,你是如何判断的?
与你的同伴交流.
4
1
2
2
4
3
解:△ABE,△DEF,△FCB △BEF均为直角三角形.
由勾股定理知
BE2=22+42=20,
EF2=22+12=5,
BF2=32+42=25,
∴BE2+EF2=BF2,
∴ △BEF是直角三角形.
叁
课堂小结
肆
课堂小结
肆
一定是直角三角形吗
勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
勾股数:满足a2+b2=c2的三个正整数
肆
课后作业
基础题:1.随堂练习 第 1,2题;习题1.2第1,2,3题
提高题:2. 习题1.2第3, 5题。
谢
谢
同课章节目录
