2.2 第4课时 估算 (共22张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 2.2 第4课时 估算 (共22张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:22:15 | ||
图片预览






文档简介
(共26张PPT)
第 4 课时 估算
第二章 实数
2.平方根与立方根
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
观察与思考
某地开辟了一块长方形荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400000m2.
(1)公园的宽大约是多少?它有1000m吗?
1000
2000
S=400000
∵2000×1000=2000000 >400000,
∴公园的宽没有1 000m.
壹
情境导入
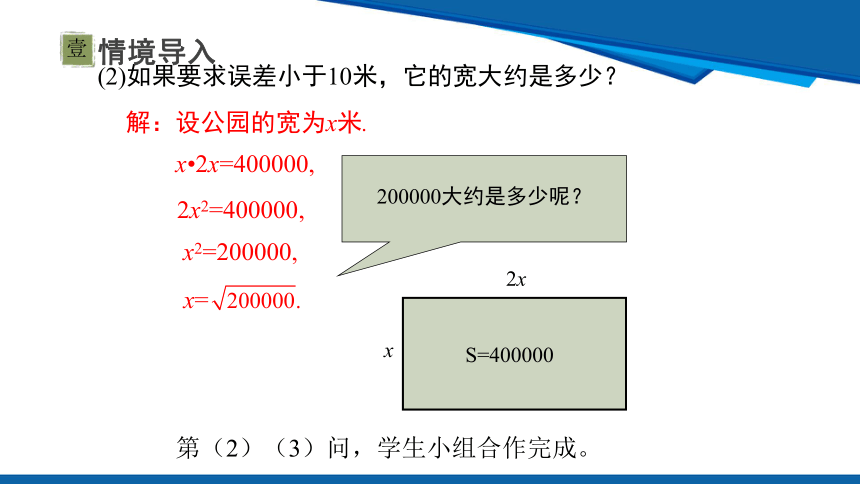
(2)如果要求误差小于10米,它的宽大约是多少?
x
2x
S=400000
x 2x=400000,
2x2=400000,
x2=200000,
x=
200000大约是多少呢?
解:设公园的宽为x米.
第(2)(3)问,学生小组合作完成。
壹
情境导入
由(1)知 x<1 000,
当 x = 500 时,2x2 = 500 000 > 400 000.
当 x = 400 时,2x2 = 320 000 < 400 000.
当 x = 450 时,2x2 = 405 000 > 400 000.
大约是多少呢?
当 x = 440 时,2x2 = 387 200 < 400 000.
所以 x = ≈ 450.
答:它的宽大约是 450 米.
壹
情境导入
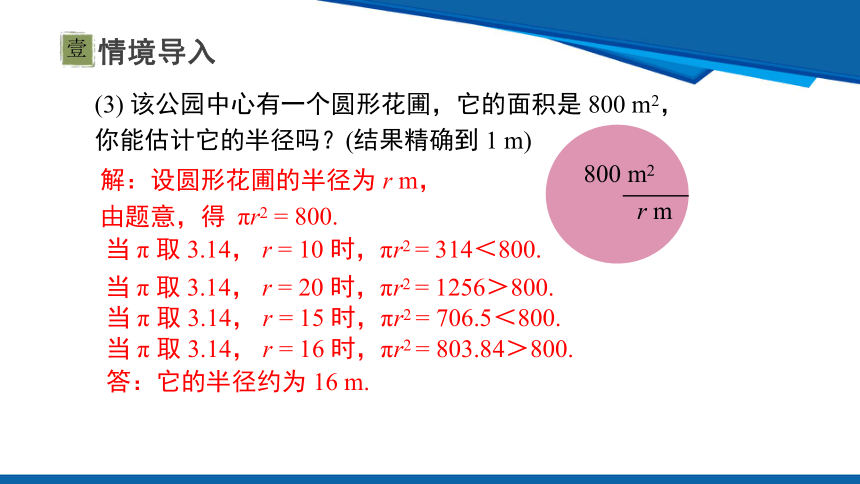
(3) 该公园中心有一个圆形花圃,它的面积是 800 m2,你能估计它的半径吗?(结果精确到 1 m)
800 m2
r m
解:设圆形花圃的半径为 r m,由题意,得
πr2 = 800.
当 π 取 3.14, r = 10 时,πr2 = 314<800.
当 π 取 3.14, r = 20 时,πr2 = 1256>800.
当 π 取 3.14, r = 15 时,πr2 = 706.5<800.
当 π 取 3.14, r = 16 时,πr2 = 803.84>800.
答:它的半径约为 16 m.
壹
新知初探
贰
新知初探
贰
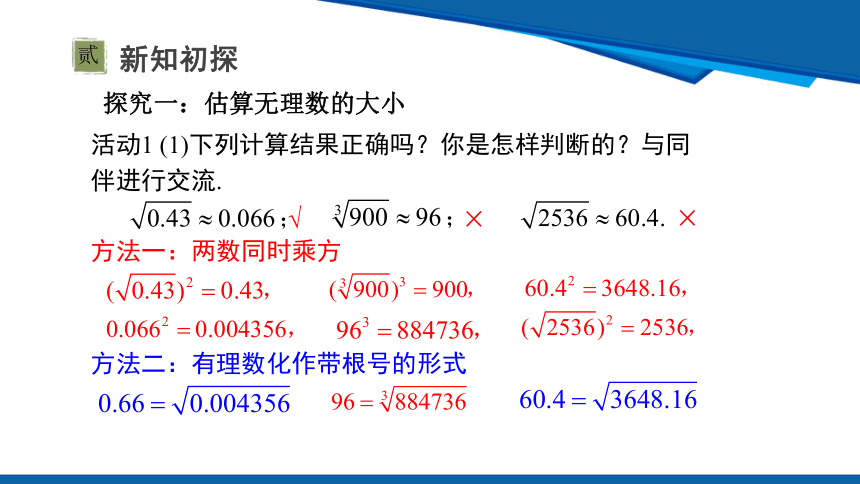
活动1 (1)下列计算结果正确吗?你是怎样判断的?与同伴进行交流.
√
×
×
方法一:两数同时乘方
方法二:有理数化作带根号的形式
探究一:估算无理数的大小
新知初探
贰
(2) 你能估算 的大小吗?(结果精确到 1)
解:因为 93 <900<103 ,
所以 .
估算无理数大小的方法:
(1) 利用乘方与开方互为逆运算来确定无理数的整数部分;
(2) 根据所要求的误差确定小数部分.
且 900 更接近 1000,
所以 .
新知初探
贰
(3)宽与长之比为 的长方形称为“黄金矩形”,你能比较比较 与 的大小吗?你是怎样想的?
解:
新知初探
贰
对于含根号的数比较大小,一般可采取下列方法:
1. 先估算含根号的数的近似值,再和另一个数进行比较;
2. 当符号相同时,把不含根号的数平方,和被开方数比较,本方法的实质是比较被开方数,被开方数越大,其算术平方根越大;
3. 若同分母或同分子的,可比较它们的分子或分母的大小.
归纳总结
新知初探
活动2 典例精析
贰
例2 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的 ,则梯子比较稳定.现有一长为 6 m 的梯子,当梯子稳定摆放时,它的顶端能达到 5.6 m 高的墙头吗
新知初探
贰
解:设梯子稳定摆放时的高度为 x m,此时梯子底端离墙的距离恰为梯子长度的 ,根据勾股定理
6
所以梯子稳定摆放时,它的顶端能够达到 5.6 m 高的墙头.
新知初探
贰
探究二:用计算器估算无理数
活动3 尝试 思考
(1)观察你的计算器面板,对于开方运算,可能用到哪些按键,利用计算器求下列各式的值(结果精确到0.0001):
① ②
新知初探
贰
用计算器开方
1
对于开平方运算,按键顺序为:
被开方数
=
对于开立方运算,按键顺序为:
被开方数
SHIFT
=
3
第二功能
对于小数与分数可以按:
S D
新知初探
贰
用计算器计算:
(1) ; (2) .
解:(1)
5.89 =
(2)
,显示 2.426 932 22.
,显示 -10.871 789 69.
-1285 =
SHIFT
新知初探
贰
(2) 任意找一个你认为很大的正数,利用计算器对它进行开平方运算,对所得结果再进行开平方运算……随着开方次数的增加,你发现了什么?
计算的结果越来越接近 1.
新知初探
贰
(2) 改用另一个小于 1 的正数试一试,看看是否仍有类似规律?
是的,结果也越来越接近 1.
道生一,一生二,二生三, 三生万物.
——《道德经》
当堂达标
叁
当堂达标
叁
1. 通过估算,比较下面各组数的大小:
解:(1) 因为
所以
所以
(2) 因为 3.852 =14.8225,
所以
叁
当堂达标
叁
2. 利用计算器求下列各式的值 (结果保留 4 个有效数字):
(2) ;
(3) ;
(4) .
(1)
解:(1)28.28.
(2)1.639.
(3)0.7616.
(4)-0.7560.
叁
叁
当堂达标
叁
3. 一个人一生平均要饮用的液体总量大约为 40 m3. 如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高?(结果精确到 1 m)
解:设圆柱的高为 x m,那么它的底面半径为 0.5x m,
则
答:这个容器大约有 4 m 高.
叁
叁
课堂小结
肆
课堂小结
肆
估算
估算的基本方法
估算在生活中的应用
使用计算器进行开方运算
用计算器开方比较数的大小
叁
肆
课后作业
基础题:1.课后习题 第 8,9,10,11,14题。
提高题:2.请学有余力的同学完成课后习题第23题
谢
谢
第 4 课时 估算
第二章 实数
2.平方根与立方根
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
观察与思考
某地开辟了一块长方形荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400000m2.
(1)公园的宽大约是多少?它有1000m吗?
1000
2000
S=400000
∵2000×1000=2000000 >400000,
∴公园的宽没有1 000m.
壹
情境导入
(2)如果要求误差小于10米,它的宽大约是多少?
x
2x
S=400000
x 2x=400000,
2x2=400000,
x2=200000,
x=
200000大约是多少呢?
解:设公园的宽为x米.
第(2)(3)问,学生小组合作完成。
壹
情境导入
由(1)知 x<1 000,
当 x = 500 时,2x2 = 500 000 > 400 000.
当 x = 400 时,2x2 = 320 000 < 400 000.
当 x = 450 时,2x2 = 405 000 > 400 000.
大约是多少呢?
当 x = 440 时,2x2 = 387 200 < 400 000.
所以 x = ≈ 450.
答:它的宽大约是 450 米.
壹
情境导入
(3) 该公园中心有一个圆形花圃,它的面积是 800 m2,你能估计它的半径吗?(结果精确到 1 m)
800 m2
r m
解:设圆形花圃的半径为 r m,由题意,得
πr2 = 800.
当 π 取 3.14, r = 10 时,πr2 = 314<800.
当 π 取 3.14, r = 20 时,πr2 = 1256>800.
当 π 取 3.14, r = 15 时,πr2 = 706.5<800.
当 π 取 3.14, r = 16 时,πr2 = 803.84>800.
答:它的半径约为 16 m.
壹
新知初探
贰
新知初探
贰
活动1 (1)下列计算结果正确吗?你是怎样判断的?与同伴进行交流.
√
×
×
方法一:两数同时乘方
方法二:有理数化作带根号的形式
探究一:估算无理数的大小
新知初探
贰
(2) 你能估算 的大小吗?(结果精确到 1)
解:因为 93 <900<103 ,
所以 .
估算无理数大小的方法:
(1) 利用乘方与开方互为逆运算来确定无理数的整数部分;
(2) 根据所要求的误差确定小数部分.
且 900 更接近 1000,
所以 .
新知初探
贰
(3)宽与长之比为 的长方形称为“黄金矩形”,你能比较比较 与 的大小吗?你是怎样想的?
解:
新知初探
贰
对于含根号的数比较大小,一般可采取下列方法:
1. 先估算含根号的数的近似值,再和另一个数进行比较;
2. 当符号相同时,把不含根号的数平方,和被开方数比较,本方法的实质是比较被开方数,被开方数越大,其算术平方根越大;
3. 若同分母或同分子的,可比较它们的分子或分母的大小.
归纳总结
新知初探
活动2 典例精析
贰
例2 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的 ,则梯子比较稳定.现有一长为 6 m 的梯子,当梯子稳定摆放时,它的顶端能达到 5.6 m 高的墙头吗
新知初探
贰
解:设梯子稳定摆放时的高度为 x m,此时梯子底端离墙的距离恰为梯子长度的 ,根据勾股定理
6
所以梯子稳定摆放时,它的顶端能够达到 5.6 m 高的墙头.
新知初探
贰
探究二:用计算器估算无理数
活动3 尝试 思考
(1)观察你的计算器面板,对于开方运算,可能用到哪些按键,利用计算器求下列各式的值(结果精确到0.0001):
① ②
新知初探
贰
用计算器开方
1
对于开平方运算,按键顺序为:
被开方数
=
对于开立方运算,按键顺序为:
被开方数
SHIFT
=
3
第二功能
对于小数与分数可以按:
S D
新知初探
贰
用计算器计算:
(1) ; (2) .
解:(1)
5.89 =
(2)
,显示 2.426 932 22.
,显示 -10.871 789 69.
-1285 =
SHIFT
新知初探
贰
(2) 任意找一个你认为很大的正数,利用计算器对它进行开平方运算,对所得结果再进行开平方运算……随着开方次数的增加,你发现了什么?
计算的结果越来越接近 1.
新知初探
贰
(2) 改用另一个小于 1 的正数试一试,看看是否仍有类似规律?
是的,结果也越来越接近 1.
道生一,一生二,二生三, 三生万物.
——《道德经》
当堂达标
叁
当堂达标
叁
1. 通过估算,比较下面各组数的大小:
解:(1) 因为
所以
所以
(2) 因为 3.852 =14.8225,
所以
叁
当堂达标
叁
2. 利用计算器求下列各式的值 (结果保留 4 个有效数字):
(2) ;
(3) ;
(4) .
(1)
解:(1)28.28.
(2)1.639.
(3)0.7616.
(4)-0.7560.
叁
叁
当堂达标
叁
3. 一个人一生平均要饮用的液体总量大约为 40 m3. 如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高?(结果精确到 1 m)
解:设圆柱的高为 x m,那么它的底面半径为 0.5x m,
则
答:这个容器大约有 4 m 高.
叁
叁
课堂小结
肆
课堂小结
肆
估算
估算的基本方法
估算在生活中的应用
使用计算器进行开方运算
用计算器开方比较数的大小
叁
肆
课后作业
基础题:1.课后习题 第 8,9,10,11,14题。
提高题:2.请学有余力的同学完成课后习题第23题
谢
谢
同课章节目录
