2.3 第1课时 二次根式与二次根式的乘除运算 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 2.3 第1课时 二次根式与二次根式的乘除运算 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:22:32 | ||
图片预览








文档简介
(共24张PPT)
第1课时 二次根式与二次根式的乘除运算
第二章 实数
3.二次根式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
问题1 什么叫作平方根?
一般地,如果一个数的平方等于 a,那么这个数叫作 a 的平方根.
问题2 什么叫作算术平方根?怎么表示它?
如果 x2 = a(x≥0),那么 x 称为 a 的算术平方根,用 表示.
问题3 什么数有平方根?
我们知道,负数没有平方根. 因此,在实数范围内开平方时,被开方数只能是非负数.
壹
新知初探
贰
新知初探
探究一:二次根式的概念及性质
贰
可以发现,这些式子我们在前面都已学习过,它们的共同特征是:
观察下列代数式:
都含有开平方运算,
并且被开方数都是非负数.
新知初探
贰
一般地,我们把形如 的式子叫作二次根式. “ a ”叫作被开方数.
注意:a 可以是数,也可以是式子.
两个必备特征
① 外形特征:含有“ ”
② 内在特征:被开方数 a≥0
二次根式的概念
新知初探
贰
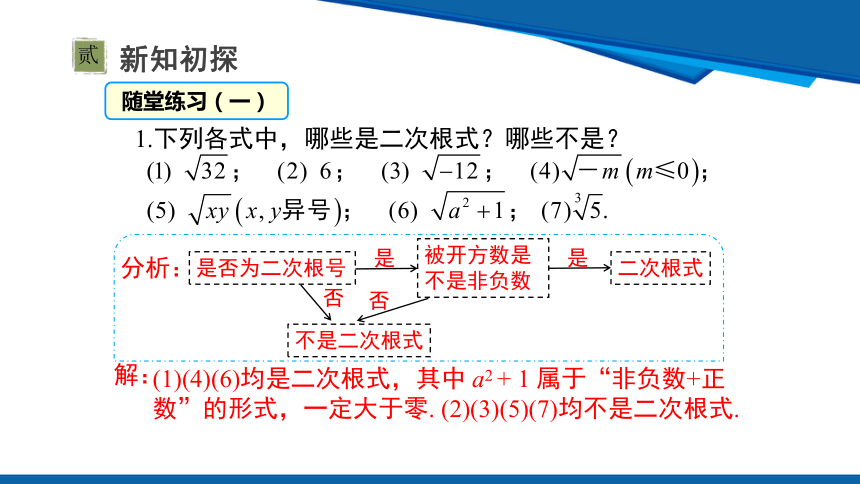
1.下列各式中,哪些是二次根式?哪些不是?
解:
(1)(4)(6)均是二次根式,其中 a2 + 1 属于“非负数+正数”的形式,一定大于零. (2)(3)(5)(7)均不是二次根式.
是否为二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
随堂练习(一)
新知初探
贰
2. 当 x 是怎样的实数时, 在实数范围内有意义
解:由 x - 2≥0,得
x≥2.
当 x≥2 时, 在实数范围内有意义.
【变式】当 x 是怎样的实数时,下列各式在实数范围内有意义?
解:由题意得 x - 1>0,
所以 x>1.
新知初探
贰
(1) 单个二次根式如 有意义的条件:
(2) 多个二次根式相加如 有意义的
条件:
(3) 二次根式作为分母如 有意义的条件:
(4) 形如 或 的式子有意义的条件:
A≥0,B≥0,… ,N≥0.
A≥0 且 B ≠ 0.
A>0.
A≥0.
(3)、(4) 表示分母与被开方数都要考虑.
归纳总结
新知初探
贰
问题1 当 x 是怎样的实数时, 在实数范围内有意义? 呢?
前者 x 为全体实数,后者 x 为非负数.
当 a>0 时, 表示 a 的算术平方根,因此 >0;当 a = 0 时, 表示 0 的算术平方根,因此 = 0. 这就是说,当 a≥0 时, ≥0.
问题2 二次根式 的被开方数 a 的取值范围是什么?它本身的取值范围又是什么?
二次根式的双重非负性
新知初探
贰
二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式 ,我们知道:
(1)a 为被开方数或式,为保证其有意义,必有 a≥0;
(2) 表示一个数或式的算术平方根,故 ≥0.
二次根式的被开方数或被开方式非负
二次根式的值非负
二次根式的双重非负性
归纳总结
新知初探
探究二:二次根式的乘除
贰
(1)计算下列各式,你能得到什么猜想
= ,
= ;
= ,
= ;
= ,
= .
6
6
新知初探
贰
= ,
6.480
= ;
(2)根据上面的猜想,估计下面每组两个式子是否相等,借助计算器验证,并与同伴进行交流.
= ,
= .
6.480
0.9255
0.9255
新知初探
贰
(a≥0,b≥0)
.
(a≥0,b>0).
商的算术平方根。
积的算术平方根。
算术平方根的积等于
算术平方根的商,
归纳总结
新知初探
贰
典例精析
例1 计算:
新知初探
贰
解:(1)原式 =
例2 计算:
(2)原式 =
(3)原式 =
(4)原式 =
新知初探
贰
解:(5)原式 =
(6)原式 =
当堂达标
叁
当堂达标
叁
1. 在括号中填写适当的数或式子使等式成立.
( )=10;
( )= 4;
2. 下列式子一定是二次根式的是( )
A. B. C. D.
A
叁
当堂达标
叁
解: (1)原式 =
3. 计算:
(2)
叁
课堂小结
肆
课堂小结
肆
二次根式
定义
带有二次根号
被开方数为非负数
二次根式的双重非负性
二次根式 中,a≥0且 ≥0
乘除法则
叁
肆
课后作业
基础题:1.课后习题 第 1,4题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
第1课时 二次根式与二次根式的乘除运算
第二章 实数
3.二次根式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
问题1 什么叫作平方根?
一般地,如果一个数的平方等于 a,那么这个数叫作 a 的平方根.
问题2 什么叫作算术平方根?怎么表示它?
如果 x2 = a(x≥0),那么 x 称为 a 的算术平方根,用 表示.
问题3 什么数有平方根?
我们知道,负数没有平方根. 因此,在实数范围内开平方时,被开方数只能是非负数.
壹
新知初探
贰
新知初探
探究一:二次根式的概念及性质
贰
可以发现,这些式子我们在前面都已学习过,它们的共同特征是:
观察下列代数式:
都含有开平方运算,
并且被开方数都是非负数.
新知初探
贰
一般地,我们把形如 的式子叫作二次根式. “ a ”叫作被开方数.
注意:a 可以是数,也可以是式子.
两个必备特征
① 外形特征:含有“ ”
② 内在特征:被开方数 a≥0
二次根式的概念
新知初探
贰
1.下列各式中,哪些是二次根式?哪些不是?
解:
(1)(4)(6)均是二次根式,其中 a2 + 1 属于“非负数+正数”的形式,一定大于零. (2)(3)(5)(7)均不是二次根式.
是否为二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
随堂练习(一)
新知初探
贰
2. 当 x 是怎样的实数时, 在实数范围内有意义
解:由 x - 2≥0,得
x≥2.
当 x≥2 时, 在实数范围内有意义.
【变式】当 x 是怎样的实数时,下列各式在实数范围内有意义?
解:由题意得 x - 1>0,
所以 x>1.
新知初探
贰
(1) 单个二次根式如 有意义的条件:
(2) 多个二次根式相加如 有意义的
条件:
(3) 二次根式作为分母如 有意义的条件:
(4) 形如 或 的式子有意义的条件:
A≥0,B≥0,… ,N≥0.
A≥0 且 B ≠ 0.
A>0.
A≥0.
(3)、(4) 表示分母与被开方数都要考虑.
归纳总结
新知初探
贰
问题1 当 x 是怎样的实数时, 在实数范围内有意义? 呢?
前者 x 为全体实数,后者 x 为非负数.
当 a>0 时, 表示 a 的算术平方根,因此 >0;当 a = 0 时, 表示 0 的算术平方根,因此 = 0. 这就是说,当 a≥0 时, ≥0.
问题2 二次根式 的被开方数 a 的取值范围是什么?它本身的取值范围又是什么?
二次根式的双重非负性
新知初探
贰
二次根式的实质是表示一个非负数(或式)的算术平方根.对于任意一个二次根式 ,我们知道:
(1)a 为被开方数或式,为保证其有意义,必有 a≥0;
(2) 表示一个数或式的算术平方根,故 ≥0.
二次根式的被开方数或被开方式非负
二次根式的值非负
二次根式的双重非负性
归纳总结
新知初探
探究二:二次根式的乘除
贰
(1)计算下列各式,你能得到什么猜想
= ,
= ;
= ,
= ;
= ,
= .
6
6
新知初探
贰
= ,
6.480
= ;
(2)根据上面的猜想,估计下面每组两个式子是否相等,借助计算器验证,并与同伴进行交流.
= ,
= .
6.480
0.9255
0.9255
新知初探
贰
(a≥0,b≥0)
.
(a≥0,b>0).
商的算术平方根。
积的算术平方根。
算术平方根的积等于
算术平方根的商,
归纳总结
新知初探
贰
典例精析
例1 计算:
新知初探
贰
解:(1)原式 =
例2 计算:
(2)原式 =
(3)原式 =
(4)原式 =
新知初探
贰
解:(5)原式 =
(6)原式 =
当堂达标
叁
当堂达标
叁
1. 在括号中填写适当的数或式子使等式成立.
( )=10;
( )= 4;
2. 下列式子一定是二次根式的是( )
A. B. C. D.
A
叁
当堂达标
叁
解: (1)原式 =
3. 计算:
(2)
叁
课堂小结
肆
课堂小结
肆
二次根式
定义
带有二次根号
被开方数为非负数
二次根式的双重非负性
二次根式 中,a≥0且 ≥0
乘除法则
叁
肆
课后作业
基础题:1.课后习题 第 1,4题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
同课章节目录
