2.3 第2课时 最简二次根式与二次根式的加减运算 课件 (共20张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 2.3 第2课时 最简二次根式与二次根式的加减运算 课件 (共20张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:22:55 | ||
图片预览








文档简介
(共20张PPT)
第2课时 最简二次根式与二次根式的加减运算
第二章 实数
3.二次根式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
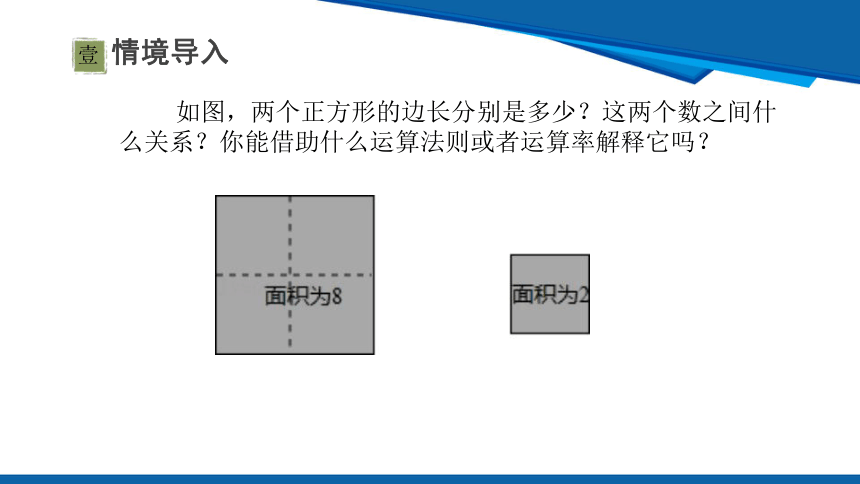
如图,两个正方形的边长分别是多少?这两个数之间什么关系?你能借助什么运算法则或者运算率解释它吗?
壹
新知初探
贰
新知初探
探究一:最简二次根式
贰
二次根式的化简
二次根式的乘法法则和除法法则
(a≥0,b≥0)
(a≥0,b>0).
(a≥0,b≥0)
(a≥0,b>0).
新知初探
贰
例3 化简:
解:(1)
(2)
(3)
(1) ; (2) ; (3) .
新知初探
贰
最简二次根式
一般地,被开方数不含分母,也不含能开得尽方的因数或因式,这样的二次根式,叫作最简二次根式.
化简时,通常要求最终结果中分母不含有根号,而且各个二次根式是最简二次根式.
新知初探
贰
例4 化简:
解:
新知初探
贰
(1) 你是怎么发现 的被开方数含有开得尽方的因数的?你是怎么判断 是最简二次根式的?
思考交流
(2) 将二次根式化成最简二次根式时,你有哪些经验与体会?与同伴进行交流
的被开方数不含分母,也不含能开得尽方的因数.
的被开方数 50 = 2×25,其中 25 开方开得尽;
新知初探
探究二:二次根式的加减
贰
解:(1)原式 =
例5 计算:
(2)原式 =
(3)原式 =
新知初探
贰
归纳总结
二次根式的加减法法则
一般地,二次根式相加减时,可以先将各个二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
2. 加减法的运算步骤:“一化简二判断三合并”.
1. 合并的前提条件:只有被开方数相同的最简二次根式才能进行合并.
要点提醒
新知初探
贰
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、乘法分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
新知初探
贰
若最简根式 与 可以合并,求 的值.
解:由题意得 2n + 1 = 2,3m - 2n = 3,
确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为 2 ,列关于待定字母的方程求解即可.
归纳
即
解得
能力提升
当堂达标
叁
当堂达标
叁
解:
计算:
叁
当堂达标
叁
解:
叁
叁
课堂小结
肆
课堂小结
肆
二次根式
的加减
二次根式的化简
最简二次根式
二次根式的加减
叁
肆
课后作业
基础题:1.课后习题 第 2,5,6题。
提高题:2.请学有余力的同学完成课后习题第9,11题
谢
谢
第2课时 最简二次根式与二次根式的加减运算
第二章 实数
3.二次根式
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
如图,两个正方形的边长分别是多少?这两个数之间什么关系?你能借助什么运算法则或者运算率解释它吗?
壹
新知初探
贰
新知初探
探究一:最简二次根式
贰
二次根式的化简
二次根式的乘法法则和除法法则
(a≥0,b≥0)
(a≥0,b>0).
(a≥0,b≥0)
(a≥0,b>0).
新知初探
贰
例3 化简:
解:(1)
(2)
(3)
(1) ; (2) ; (3) .
新知初探
贰
最简二次根式
一般地,被开方数不含分母,也不含能开得尽方的因数或因式,这样的二次根式,叫作最简二次根式.
化简时,通常要求最终结果中分母不含有根号,而且各个二次根式是最简二次根式.
新知初探
贰
例4 化简:
解:
新知初探
贰
(1) 你是怎么发现 的被开方数含有开得尽方的因数的?你是怎么判断 是最简二次根式的?
思考交流
(2) 将二次根式化成最简二次根式时,你有哪些经验与体会?与同伴进行交流
的被开方数不含分母,也不含能开得尽方的因数.
的被开方数 50 = 2×25,其中 25 开方开得尽;
新知初探
探究二:二次根式的加减
贰
解:(1)原式 =
例5 计算:
(2)原式 =
(3)原式 =
新知初探
贰
归纳总结
二次根式的加减法法则
一般地,二次根式相加减时,可以先将各个二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
2. 加减法的运算步骤:“一化简二判断三合并”.
1. 合并的前提条件:只有被开方数相同的最简二次根式才能进行合并.
要点提醒
新知初探
贰
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、乘法分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
新知初探
贰
若最简根式 与 可以合并,求 的值.
解:由题意得 2n + 1 = 2,3m - 2n = 3,
确定可以合并的二次根式中字母取值的方法:利用被开方数相同,指数都为 2 ,列关于待定字母的方程求解即可.
归纳
即
解得
能力提升
当堂达标
叁
当堂达标
叁
解:
计算:
叁
当堂达标
叁
解:
叁
叁
课堂小结
肆
课堂小结
肆
二次根式
的加减
二次根式的化简
最简二次根式
二次根式的加减
叁
肆
课后作业
基础题:1.课后习题 第 2,5,6题。
提高题:2.请学有余力的同学完成课后习题第9,11题
谢
谢
同课章节目录
