4.2 第1课时 “均匀”的量 课件(共20张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 4.2 第1课时 “均匀”的量 课件(共20张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第1课时 “均匀”变化的量
第四章 一次函数
2.认识一次函数
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
一个滴水的水龙头一年漏水量大约有多少?够一个人一年使用吗?先猜一猜,再设计一个方案具体估算一下,并与同伴交流。
2020年,我国人均生活用水量:城镇(含公共用水)207L/d,农村100L/d。
壹
新知初探
贰
新知初探
探究一:认识一次函数
贰
将水龙头拧到适当位置,造成滴漏现象,在下方放一个量杯,每隔 1min 记录量杯中的水量,填入表格,并在坐标纸上描出(t,V)对应的点。思考漏水量变化规律,估计一天漏水量。
时间 t/min 1 2 3 4 5 6 7 8 9 10
漏水量v/ml
新知初探
贰
展示小明的实验数据。请你根据小明得到的数据,在坐标纸上描出(t,v)对应的点,并据此估计,小明实验用的这个水龙头一天漏水量有多少?一年呢?够一个人一年使用的吗?
时间t/min 1 2 3 4 5 6 7 8 9 10
漏水量/ml 5.5 11 16.5 22.0 27.5 33.0 38.5 44.0 49.5 55.0
问题2:你的实验结果与小明的实验结果有何异同?
问题1:分析小明实验数据,你能帮他写出漏水量V与时间t 之间的关系吗?
v = 5.5t
新知初探
贰
(3)假如漏水严重一些,表格、图像和表达式可能会发生什么变化?为什么?
活动2 思考交流
分享各组的实验结果,并交流下列问题:
(1)比较各组的实验数据与结果,有什么共同之处,又有什么不同之处?
(2)引起各组数据不一致的因素有哪些?这些因素的差别
对表格、图象和表达式的影响分别体现在哪些方面?
新知初探
探究二:均匀变化的量
贰
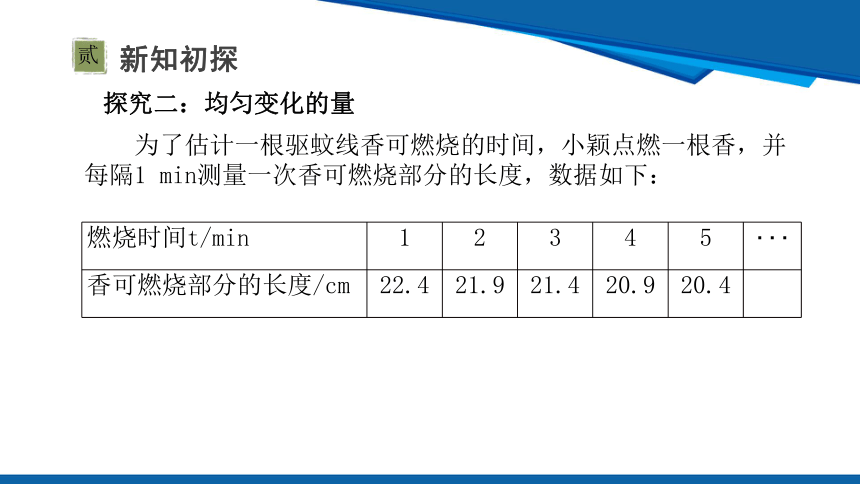
燃烧时间t/min 1 2 3 4 5
香可燃烧部分的长度/cm 22.4 21.9 21.4 20.9 20.4
为了估计一根驱蚊线香可燃烧的时间,小颖点燃一根香,并
每隔1 min测量一次香可燃烧部分的长度,数据如下:
新知初探
贰
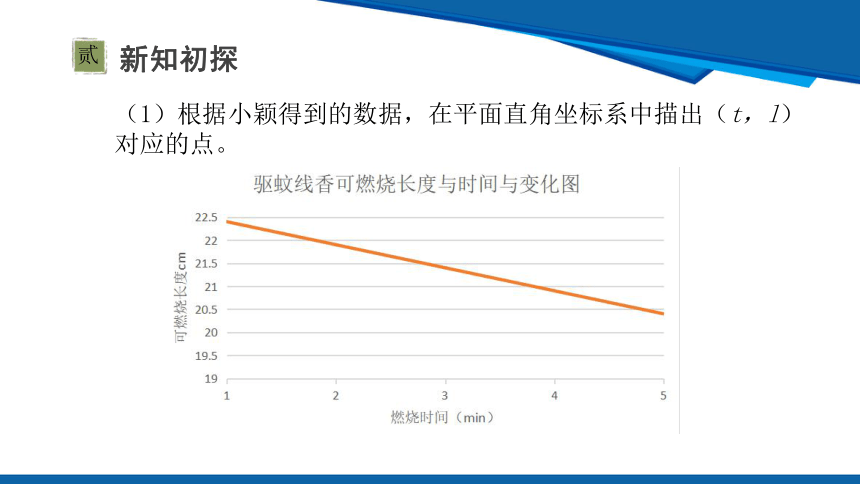
(1)根据小颖得到的数据,在平面直角坐标系中描出(t,l)对应的点。
新知初探
贰
(2)估计燃烧10 min后这根香可燃烧部分的长度,并说明理由。
(3)估计这根香可燃烧的时间,并说明理由。
(4)试写出这根香可燃烧部分的长度l与燃烧时间t的关系式。
t=44.8min
l=22.4-0.5×10=17.4
l=22.4-0.5t
新知初探
贰
在小颖的实验中,燃烧时间每增加1 min,香可燃烧部分的长度就减少0.5 cm。也就是说,随着时间的增加,香可燃烧部分的长度在“均匀”地减少。为什么香的燃烧会有这样的“均匀”变化呢?与同伴进行交流。
所谓“均匀”变化是指:一个变量增加固定的数值时,另一个变量的改变量是相同的。
当堂达标
叁
当堂达标
叁
解:由题知,
因为钢球加热后温度每增加1℃,体积增加0.051cm3,
所以温度由0℃增加到t℃时,体积就增加了0.051t cm3.
又钢球在0℃时,体积是1000cm3,
所以体积V关于温度t的函数解析式为:V=1000+0.051t.
1.一个钢球在0℃时,体积是1000cm3,加热后温度每增加1℃,体积增加0.051cm3,写出体积V关于温度t的函数解析式.
叁
当堂达标
叁
2.一根弹簧原长12厘米,每挂2千克物体,伸长1厘米.若挂x千克物体后,弹簧的长度y是多少厘米?
叁
叁
当堂达标
叁
3.某汽车在加油后开始匀速行驶.已知汽车行驶到20km时,油箱中剩油58.4L.行驶到50km时,油箱中剩油56L,如果油箱余油量是均匀变化的,请油箱中剩余油量y(L)与汽车行驶路程x(km)之间的关系.
解:由题意 可得:
y=60﹣0.08x(0≤x≤750)
叁
叁
当堂达标
叁
4.某油桶有油20升,现在有一进油管和一出油管,进油管每分钟进油4升,出油管每分钟出油6升,现同时打开两管.请写出油桶中剩油量Q(升)与开管时间t(分)之间的函数关系式。
解:Q=20﹣2t
叁
叁
课堂小结
肆
课堂小结
肆
“均匀”变化的量
列举“均匀”变化的现象
均匀变化的量
叁
肆
课后作业
基础题:1.课后习题 第 2,3,4题。
提高题:2.请学有余力的同学完成课后习题第6,7题
谢
谢
第1课时 “均匀”变化的量
第四章 一次函数
2.认识一次函数
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
一个滴水的水龙头一年漏水量大约有多少?够一个人一年使用吗?先猜一猜,再设计一个方案具体估算一下,并与同伴交流。
2020年,我国人均生活用水量:城镇(含公共用水)207L/d,农村100L/d。
壹
新知初探
贰
新知初探
探究一:认识一次函数
贰
将水龙头拧到适当位置,造成滴漏现象,在下方放一个量杯,每隔 1min 记录量杯中的水量,填入表格,并在坐标纸上描出(t,V)对应的点。思考漏水量变化规律,估计一天漏水量。
时间 t/min 1 2 3 4 5 6 7 8 9 10
漏水量v/ml
新知初探
贰
展示小明的实验数据。请你根据小明得到的数据,在坐标纸上描出(t,v)对应的点,并据此估计,小明实验用的这个水龙头一天漏水量有多少?一年呢?够一个人一年使用的吗?
时间t/min 1 2 3 4 5 6 7 8 9 10
漏水量/ml 5.5 11 16.5 22.0 27.5 33.0 38.5 44.0 49.5 55.0
问题2:你的实验结果与小明的实验结果有何异同?
问题1:分析小明实验数据,你能帮他写出漏水量V与时间t 之间的关系吗?
v = 5.5t
新知初探
贰
(3)假如漏水严重一些,表格、图像和表达式可能会发生什么变化?为什么?
活动2 思考交流
分享各组的实验结果,并交流下列问题:
(1)比较各组的实验数据与结果,有什么共同之处,又有什么不同之处?
(2)引起各组数据不一致的因素有哪些?这些因素的差别
对表格、图象和表达式的影响分别体现在哪些方面?
新知初探
探究二:均匀变化的量
贰
燃烧时间t/min 1 2 3 4 5
香可燃烧部分的长度/cm 22.4 21.9 21.4 20.9 20.4
为了估计一根驱蚊线香可燃烧的时间,小颖点燃一根香,并
每隔1 min测量一次香可燃烧部分的长度,数据如下:
新知初探
贰
(1)根据小颖得到的数据,在平面直角坐标系中描出(t,l)对应的点。
新知初探
贰
(2)估计燃烧10 min后这根香可燃烧部分的长度,并说明理由。
(3)估计这根香可燃烧的时间,并说明理由。
(4)试写出这根香可燃烧部分的长度l与燃烧时间t的关系式。
t=44.8min
l=22.4-0.5×10=17.4
l=22.4-0.5t
新知初探
贰
在小颖的实验中,燃烧时间每增加1 min,香可燃烧部分的长度就减少0.5 cm。也就是说,随着时间的增加,香可燃烧部分的长度在“均匀”地减少。为什么香的燃烧会有这样的“均匀”变化呢?与同伴进行交流。
所谓“均匀”变化是指:一个变量增加固定的数值时,另一个变量的改变量是相同的。
当堂达标
叁
当堂达标
叁
解:由题知,
因为钢球加热后温度每增加1℃,体积增加0.051cm3,
所以温度由0℃增加到t℃时,体积就增加了0.051t cm3.
又钢球在0℃时,体积是1000cm3,
所以体积V关于温度t的函数解析式为:V=1000+0.051t.
1.一个钢球在0℃时,体积是1000cm3,加热后温度每增加1℃,体积增加0.051cm3,写出体积V关于温度t的函数解析式.
叁
当堂达标
叁
2.一根弹簧原长12厘米,每挂2千克物体,伸长1厘米.若挂x千克物体后,弹簧的长度y是多少厘米?
叁
叁
当堂达标
叁
3.某汽车在加油后开始匀速行驶.已知汽车行驶到20km时,油箱中剩油58.4L.行驶到50km时,油箱中剩油56L,如果油箱余油量是均匀变化的,请油箱中剩余油量y(L)与汽车行驶路程x(km)之间的关系.
解:由题意 可得:
y=60﹣0.08x(0≤x≤750)
叁
叁
当堂达标
叁
4.某油桶有油20升,现在有一进油管和一出油管,进油管每分钟进油4升,出油管每分钟出油6升,现同时打开两管.请写出油桶中剩油量Q(升)与开管时间t(分)之间的函数关系式。
解:Q=20﹣2t
叁
叁
课堂小结
肆
课堂小结
肆
“均匀”变化的量
列举“均匀”变化的现象
均匀变化的量
叁
肆
课后作业
基础题:1.课后习题 第 2,3,4题。
提高题:2.请学有余力的同学完成课后习题第6,7题
谢
谢
同课章节目录
