4.4 第2课时 借助单个一次函数图象解决实际问题 课件(共26张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 4.4 第2课时 借助单个一次函数图象解决实际问题 课件(共26张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:30:31 | ||
图片预览





文档简介
(共26张PPT)
第2课时 借助单个一次函数图象解决实际问题
第四章 一次函数
4.一次函数的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
如图所示是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成。小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短。设单层部分的长度为x cm,双层部分的长度为y cm,经测量,得到如下数据:
单层部分的长度x/cm … 4 6 8 10 …
双层部分的长度y/cm … 73 72 71 70 …
(1)根据表中数据的规律,完成以上表格,并直接写出y关于x的函数表达式;
(2)根据小敏的身高和习惯,挎带的长度为120 cm时,背起来正合适,请求出此时单层部分的长度。
叁
叁
壹
新知初探
贰
新知初探
探究一:单个一次函数的应用
贰
行驶路程 x=0 时,y 的值
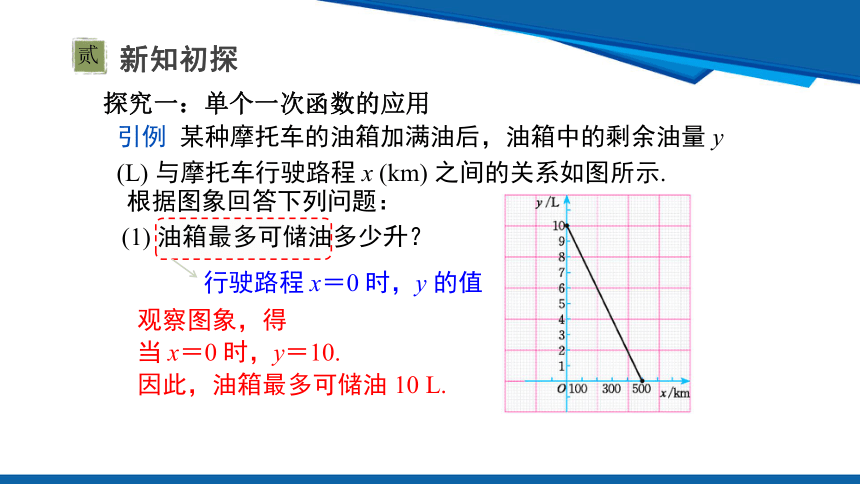
引例 某种摩托车的油箱加满油后,油箱中的剩余油量 y (L) 与摩托车行驶路程 x (km) 之间的关系如图所示.
根据图象回答下列问题:
观察图象,得
当 x=0 时,y=10.
因此,油箱最多可储油 10 L.
(1) 油箱最多可储油多少升?
新知初探
贰
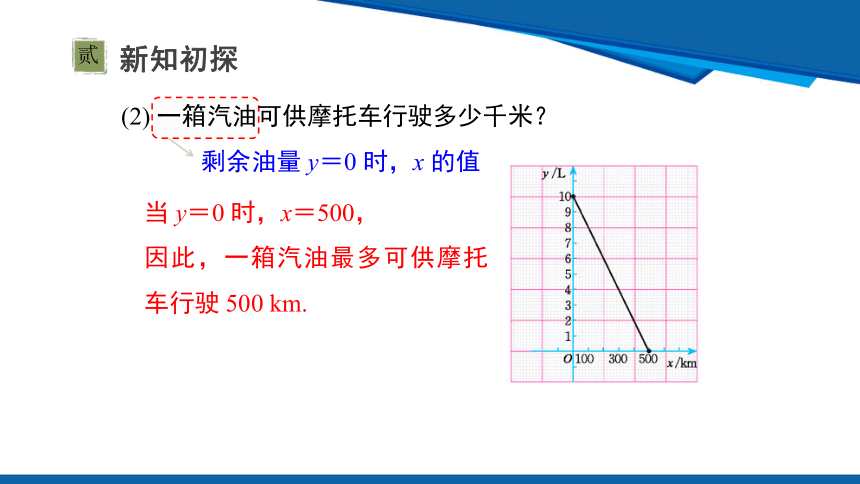
剩余油量 y=0 时,x 的值
(2) 一箱汽油可供摩托车行驶多少千米?
当 y=0 时,x=500,
因此,一箱汽油最多可供摩托车行驶 500 km.
新知初探
贰
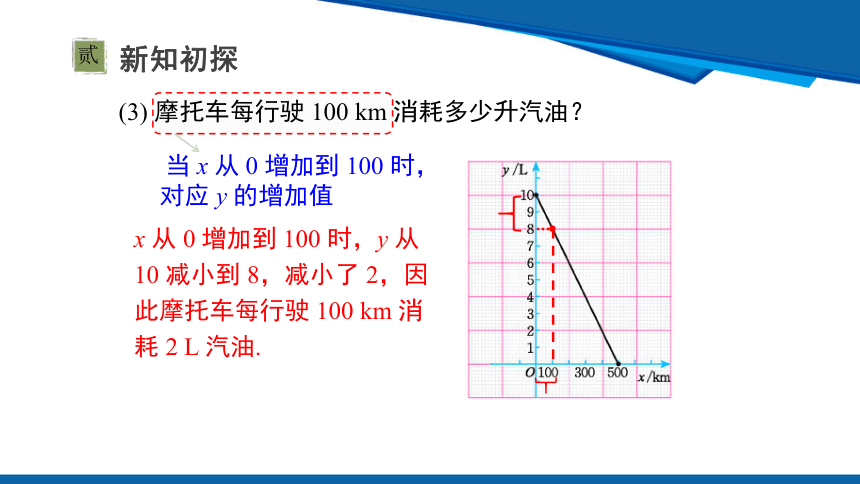
当 x 从 0 增加到 100 时,对应 y 的增加值
(3) 摩托车每行驶 100 km 消耗多少升汽油?
x 从 0 增加到 100 时,y 从 10 减小到 8,减小了 2,因此摩托车每行驶 100 km 消耗 2 L 汽油.
新知初探
贰
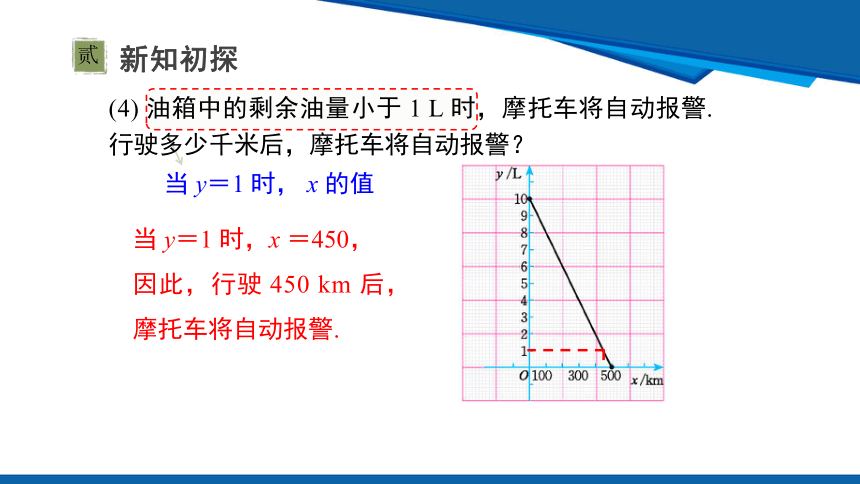
当 y=1 时, x 的值
(4) 油箱中的剩余油量小于 1 L 时,摩托车将自动报警.行驶多少千米后,摩托车将自动报警?
当 y=1 时,x =450,
因此,行驶 450 km 后,摩托车将自动报警.
新知初探
贰
如何解答实际情境函数图象的信息?
1. 理解横纵坐标分别表示的实际意义;
3. 利用数形结合的思想:
2. 分析已知条件,通过作 x 轴或 y 轴的垂线, 在图象上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值;
归纳总结
将“数”转化为“形”
由“形”定“数”
新知初探
探究二:典例精析:
贰
例2:由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.
蓄水量 V (万m3) 与干旱持续时间 t (天) 的关系如图所示.
根据图象回答下列问题:
新知初探
贰
(1) 水库干旱前的蓄水量是多少?
蓄水量 V (万m3) 与干旱持续时间 t (天) 的关系图
解:(1) 蓄水量是 1200 万m3.
新知初探
贰
由图象可知 b=1200,
图象又过点(50,200),
则有 50k+b=200,
所以 b=1200,k=﹣20,
一次函数的表达式为:
V=-20t+1200,
当 t=23 时,解得V=740.
干旱持续 23 天蓄水量是 740 万m3.
(2) 干旱持续 10 天,蓄水量是多少 干旱持续 23 天呢
(2) 干旱持续 10 天蓄水量是 1000 万m3.
表达式法
干旱持续 23 天蓄水量是 740 万m3.
新知初探
贰
(3) 蓄水量小于 400 万m3时,将发出严重干旱警报.干旱持续多少天后将发出严重干旱警报
(3) 40 天后.
新知初探
贰
V=0
(4) 按照这个规律,预计干旱持续多少天水库将干涸?
预计干旱持续 60 天水库将干涸.
由 (2) 得,
一次函数的表达式为:
V=﹣20t+1200,
当 V=0 时,解得 t=60.
表达式法
新知初探
贰
探究三:一次函数与一元一次方程
如图是某一次函数的图象,根据图象填空:
(1) 当 y=0 时,x = ;
(2) 这个函数的表达式是 ;
(3) 图象与 x 轴交点的
坐标_________;
(4) 一元一次方程 0.5x + 1 = 0
的解是________.
-2
(-2,0)
x =﹣2
y=0.5x+1
新知初探
贰
一元一次方程 0.5x+1=0 与一次函数 y=0.5x+1 有什么联系?
议一议
2
O
1
3
1
2
3
-1
-2
-3
-1
-2
-3
x
y
1.从“数”的方面看,当一次函数 y = 0.5x + 1 的因变量的值为 0时,相应的自变量的值即为方程 0.5x + 1 = 0 的解.
2.从“形”的方面看,函数
y = 0.5x + 1 与 x 轴交点的横坐标,即为方程 0.5x + 1 = 0 的解.
新知初探
贰
我们知道任何一元一次方程都可以转化 kx + b = 0 的形式,你能用函数的观点解释这个方程吗
归纳总结
求一元一次方程 kx + b = 0
的解
一次函数 y = kx+b
中,y = 0时 x 的值
求直线 y = kx+b与
x 轴交点的横坐标
数
形
数形结合
y
x
o
(x,0)
当堂达标
叁
当堂达标
叁
1.已知方程 kx+b=0 的解是 x=,则函数 y=kx+b 的图象可能是 ( )
D
叁
叁
叁
当堂达标
叁
2.已知一次函数 y=ax+b 的图象如图所示:
(1) 关于 x 的方程 ax+b=0 的解是________;
(2) 关于 x 的方程 ax+b=1 的解是________;
(3) 关于 x 的方程 ax+b+1=0 的解是________.
x=2
x=4
x=0
叁
叁
叁
当堂达标
叁
3.(跨学科融合) 某生物小组观察一种植物的生长情况,得到植物高度 y (厘米) 与观察时间 x (天) 之间的关系如图所示(点 A,B,C 在同一条直线上,直线 CD 平行于 x 轴).
50
(1) 由图象可知,从观察时起,该植物______天以后停止长高;
叁
叁
叁
当堂达标
叁
(2)求直线 AC 的函数表达式,并求该植物最高为多少厘米?
叁
叁
叁
课堂小结
肆
课堂小结
肆
解答实际情境函数图
象信息问题的方法:
一次函数的应用
一次函数与一元一次方程的关系
单个一次函数图象的应用
法一
图象观察法
1.只用语言叙述或用表格、图象提供一次函数的情境时,应先求出表达式,再利用函数性质解决问题.
法二
关系式计算法
2.给出一次函数表达式,直接应用次函数的性质解决问题.
叁
叁
肆
课后作业
基础题:1.课后习题 第 3,6题。
提高题:2.请学有余力的同学完成课后习题第9题
谢
谢
第2课时 借助单个一次函数图象解决实际问题
第四章 一次函数
4.一次函数的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
如图所示是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成。小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短。设单层部分的长度为x cm,双层部分的长度为y cm,经测量,得到如下数据:
单层部分的长度x/cm … 4 6 8 10 …
双层部分的长度y/cm … 73 72 71 70 …
(1)根据表中数据的规律,完成以上表格,并直接写出y关于x的函数表达式;
(2)根据小敏的身高和习惯,挎带的长度为120 cm时,背起来正合适,请求出此时单层部分的长度。
叁
叁
壹
新知初探
贰
新知初探
探究一:单个一次函数的应用
贰
行驶路程 x=0 时,y 的值
引例 某种摩托车的油箱加满油后,油箱中的剩余油量 y (L) 与摩托车行驶路程 x (km) 之间的关系如图所示.
根据图象回答下列问题:
观察图象,得
当 x=0 时,y=10.
因此,油箱最多可储油 10 L.
(1) 油箱最多可储油多少升?
新知初探
贰
剩余油量 y=0 时,x 的值
(2) 一箱汽油可供摩托车行驶多少千米?
当 y=0 时,x=500,
因此,一箱汽油最多可供摩托车行驶 500 km.
新知初探
贰
当 x 从 0 增加到 100 时,对应 y 的增加值
(3) 摩托车每行驶 100 km 消耗多少升汽油?
x 从 0 增加到 100 时,y 从 10 减小到 8,减小了 2,因此摩托车每行驶 100 km 消耗 2 L 汽油.
新知初探
贰
当 y=1 时, x 的值
(4) 油箱中的剩余油量小于 1 L 时,摩托车将自动报警.行驶多少千米后,摩托车将自动报警?
当 y=1 时,x =450,
因此,行驶 450 km 后,摩托车将自动报警.
新知初探
贰
如何解答实际情境函数图象的信息?
1. 理解横纵坐标分别表示的实际意义;
3. 利用数形结合的思想:
2. 分析已知条件,通过作 x 轴或 y 轴的垂线, 在图象上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值;
归纳总结
将“数”转化为“形”
由“形”定“数”
新知初探
探究二:典例精析:
贰
例2:由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.
蓄水量 V (万m3) 与干旱持续时间 t (天) 的关系如图所示.
根据图象回答下列问题:
新知初探
贰
(1) 水库干旱前的蓄水量是多少?
蓄水量 V (万m3) 与干旱持续时间 t (天) 的关系图
解:(1) 蓄水量是 1200 万m3.
新知初探
贰
由图象可知 b=1200,
图象又过点(50,200),
则有 50k+b=200,
所以 b=1200,k=﹣20,
一次函数的表达式为:
V=-20t+1200,
当 t=23 时,解得V=740.
干旱持续 23 天蓄水量是 740 万m3.
(2) 干旱持续 10 天,蓄水量是多少 干旱持续 23 天呢
(2) 干旱持续 10 天蓄水量是 1000 万m3.
表达式法
干旱持续 23 天蓄水量是 740 万m3.
新知初探
贰
(3) 蓄水量小于 400 万m3时,将发出严重干旱警报.干旱持续多少天后将发出严重干旱警报
(3) 40 天后.
新知初探
贰
V=0
(4) 按照这个规律,预计干旱持续多少天水库将干涸?
预计干旱持续 60 天水库将干涸.
由 (2) 得,
一次函数的表达式为:
V=﹣20t+1200,
当 V=0 时,解得 t=60.
表达式法
新知初探
贰
探究三:一次函数与一元一次方程
如图是某一次函数的图象,根据图象填空:
(1) 当 y=0 时,x = ;
(2) 这个函数的表达式是 ;
(3) 图象与 x 轴交点的
坐标_________;
(4) 一元一次方程 0.5x + 1 = 0
的解是________.
-2
(-2,0)
x =﹣2
y=0.5x+1
新知初探
贰
一元一次方程 0.5x+1=0 与一次函数 y=0.5x+1 有什么联系?
议一议
2
O
1
3
1
2
3
-1
-2
-3
-1
-2
-3
x
y
1.从“数”的方面看,当一次函数 y = 0.5x + 1 的因变量的值为 0时,相应的自变量的值即为方程 0.5x + 1 = 0 的解.
2.从“形”的方面看,函数
y = 0.5x + 1 与 x 轴交点的横坐标,即为方程 0.5x + 1 = 0 的解.
新知初探
贰
我们知道任何一元一次方程都可以转化 kx + b = 0 的形式,你能用函数的观点解释这个方程吗
归纳总结
求一元一次方程 kx + b = 0
的解
一次函数 y = kx+b
中,y = 0时 x 的值
求直线 y = kx+b与
x 轴交点的横坐标
数
形
数形结合
y
x
o
(x,0)
当堂达标
叁
当堂达标
叁
1.已知方程 kx+b=0 的解是 x=,则函数 y=kx+b 的图象可能是 ( )
D
叁
叁
叁
当堂达标
叁
2.已知一次函数 y=ax+b 的图象如图所示:
(1) 关于 x 的方程 ax+b=0 的解是________;
(2) 关于 x 的方程 ax+b=1 的解是________;
(3) 关于 x 的方程 ax+b+1=0 的解是________.
x=2
x=4
x=0
叁
叁
叁
当堂达标
叁
3.(跨学科融合) 某生物小组观察一种植物的生长情况,得到植物高度 y (厘米) 与观察时间 x (天) 之间的关系如图所示(点 A,B,C 在同一条直线上,直线 CD 平行于 x 轴).
50
(1) 由图象可知,从观察时起,该植物______天以后停止长高;
叁
叁
叁
当堂达标
叁
(2)求直线 AC 的函数表达式,并求该植物最高为多少厘米?
叁
叁
叁
课堂小结
肆
课堂小结
肆
解答实际情境函数图
象信息问题的方法:
一次函数的应用
一次函数与一元一次方程的关系
单个一次函数图象的应用
法一
图象观察法
1.只用语言叙述或用表格、图象提供一次函数的情境时,应先求出表达式,再利用函数性质解决问题.
法二
关系式计算法
2.给出一次函数表达式,直接应用次函数的性质解决问题.
叁
叁
肆
课后作业
基础题:1.课后习题 第 3,6题。
提高题:2.请学有余力的同学完成课后习题第9题
谢
谢
同课章节目录
