4.4 第3课时 借助两个一次函数图象解决实际问题 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 4.4 第3课时 借助两个一次函数图象解决实际问题 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
第3课时 借助两个一次函数图象解决实际问题
第四章 一次函数
4.一次函数的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
从图象中获取信息的方法:
1.弄清函数图象横、纵坐标分别表示什么,图象上最高点、最低点的意义
2.上升线表示函数值随自变量的增大而增大;下降线表示函数值随自变量的增大而减小;水平线表示函数值不随自变量的变化而变化.
3.直线倾斜程度大,表示函数值随自变量变化迅速;直线倾斜程度小,表示函数值随自变量变化缓慢.
特别提醒:一次函数图象是直线,自变量有取值范围时就变成线段或射线;k 相同则线平行
叁
叁
壹
新知初探
贰
新知初探
探究一:两个一次函数的应用
贰
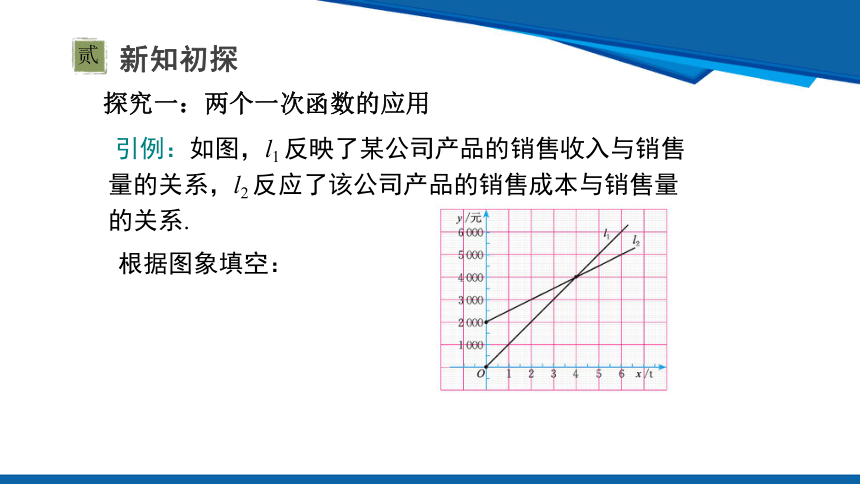
引例:如图,l1 反映了某公司产品的销售收入与销售量的关系,l2 反应了该公司产品的销售成本与销售量的关系.
根据图象填空:
新知初探
贰
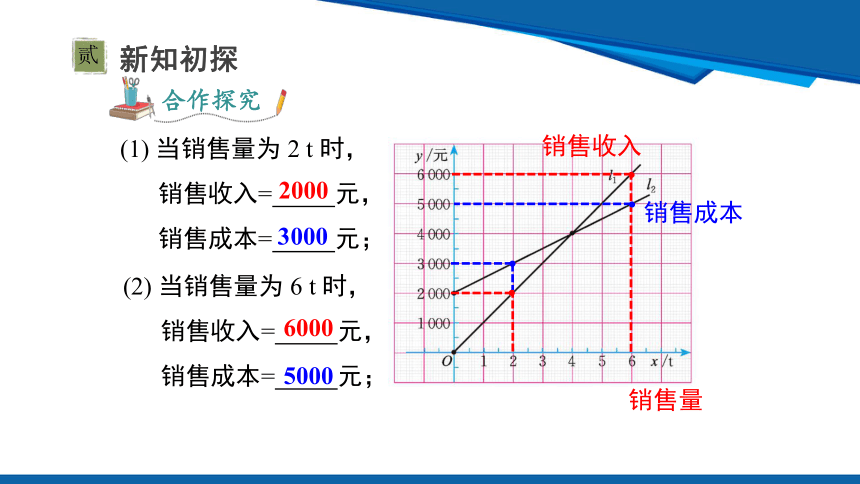
合作探究
(2) 当销售量为 6 t 时,
销售收入= 元,
销售成本= 元;
(1) 当销售量为 2 t 时,
销售收入= 元,
销售成本= 元;
2000
3000
6000
5000
销售量
销售收入
销售成本
新知初探
贰
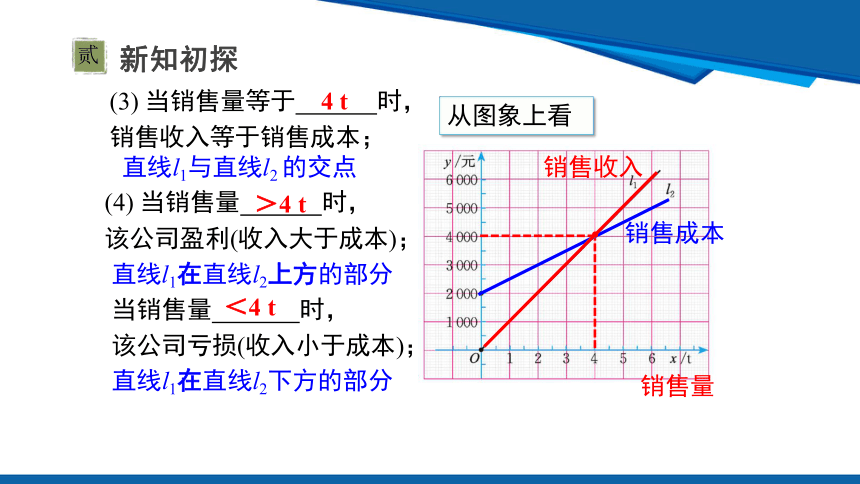
(3) 当销售量等于 时,
销售收入等于销售成本;
4 t
(4) 当销售量 时,
该公司盈利(收入大于成本);
>4 t
<4 t
销售量
销售收入
销售成本
当销售量 时,
该公司亏损(收入小于成本);
直线l1与直线l2 的交点
直线l1在直线l2上方的部分
直线l1在直线l2下方的部分
从图象上看
新知初探
贰
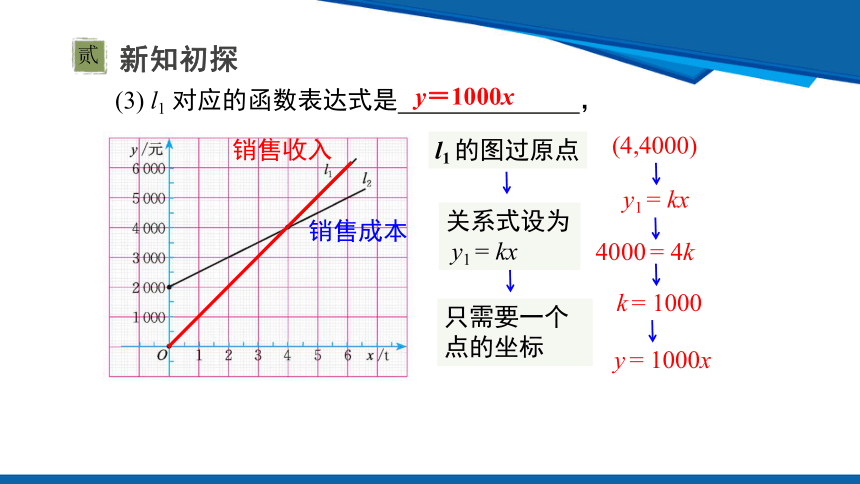
(3) l1 对应的函数表达式是 ,
y=1000x
销售收入
销售成本
l1 的图过原点
(4,4000)
y1 = kx
4000 = 4k
k = 1000
y = 1000x
关系式设为
y1 = kx
只需要一个点的坐标
新知初探
贰
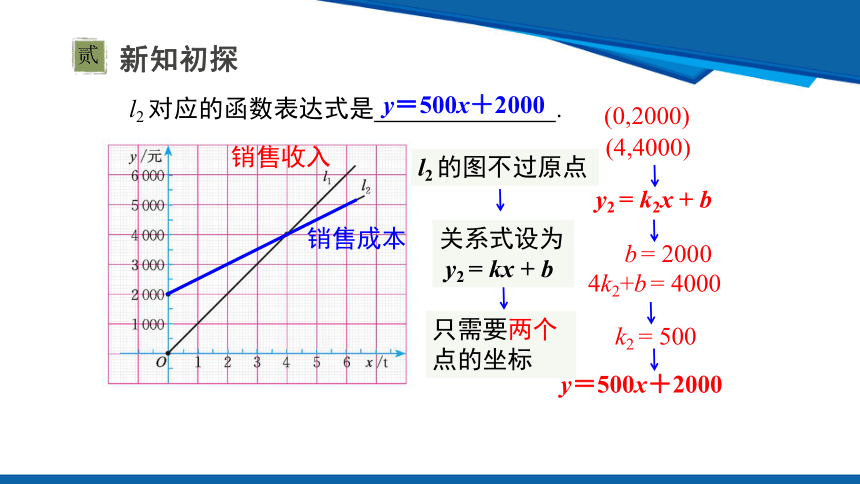
l2 对应的函数表达式是 .
y=500x+2000
l2 的图不过原点
(4,4000)
y2 = k2x + b
k2 = 500
关系式设为
y2 = kx + b
只需要两个点的坐标
(0,2000)
b = 2000
4k2+b = 4000
y=500x+2000
销售收入
销售成本
新知初探
贰
l1 对应的一次函数 y=k1x +b1中,k1 和 b1的实际意义各是什么?
想一想
k1表示每销售1吨产品,可收入1000元;
b1表示未销售时,销售收入为0元;
k2表示每销售1吨产品的成本为500元;
b2表示未销售时,为销售所花的成本为2000元;
y=1000x
l2对应的一次函数 y=k2x +b2 中,k2 和 b2 的实际意义各是什么?
y=500x+2000
新知初探
探究二:
贰
例3 图4-11是某景区游览路线示意图。甲在观景台1联系乙,发现乙在观景台2,于是沿着游览路线追赶乙。图4-12中l ,l 分别表示甲、乙两人到观景台1的路程s(单位:m)与追赶时间t(单位:min)之间的关系。
假设甲、乙两人保持现有的速度,根据图象回答下列问题:
新知初探
贰
(1)哪条线表示甲到观景台1的 路程与追赶时间之间的关系?
(2)甲和乙哪个人的速度快?
(3)30 min内甲能否追上乙?
假设甲、乙两人保持现有的速度,根据图象回答下列问题:
新知初探
贰
解:(1)当t = 0时,甲到观景台1的路程为0m,即s = 0,故l 表示甲到观景台1的路程与追赶时间之间的关系。
(2)t从0增加到20时,l1上点的纵坐标增加了1000,l2上点的纵坐标增加了600,即20 min内,甲行走了1000 m,乙行走了600 m,所以甲的速度快。
新知初探
贰
(3)如图4 - 13,延长l1,l2,可以看出,当t = 30时,l1上的对应点在l 上对应点的下方,这表明,30 min时甲尚未追上乙。
(4)在图4 - 13中,l1与l 交点P的纵坐标小于(800 + 1300 = )2100,这说明,甲能在到达观景台3前追上乙。
(5)k1表示甲的速度,k2表示乙的速度。甲的速度是50 m/min,乙的速度是30 m/min。
当堂达标
叁
当堂达标
叁
1.甲无人机从地面起飞,乙无人机从距离地面 20 m 高的楼顶起飞,两架无人机同时匀速上升 10 s.
甲、乙两架无人机所在的位置距离地面的高度 y (m) 与无人机上升的时间 x (s) 之间的关系如图所示.下列说法正确的是( )
A. 5 s时,两架无人机都上升了40 m
B. 10 s 时,两架无人机的高度差为 20 m
C. 乙无人机上升的速度为 8 m/s
D. 10 s 时,甲无人机距离地面的高度
是 60 m
B
叁
叁
当堂达标
叁
2. 如图,射线 OA、BA 分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中 s、t 分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
解析:根据图象可得出:甲的速度为
120÷5 = 24 (km/h),
乙的速度为 (120﹣4)÷5 = 23.2 (km/h),
速度差为 24 - 23.2 = 0.8 (km/h).
0.8
叁
叁
当堂达标
叁
3. 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度 y (厘米) 与燃烧时间 x (时) 之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧
前的高度分别是 ,
从点燃到燃尽所用的时间
分别是 .
30 厘米、25 厘米
2时、2.5时
叁
叁
当堂达标
叁
(2)分别求甲、乙两根蜡烛燃烧时 y 与 x 之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?
在什么时间段内,甲蜡烛比乙蜡烛高?
在什么时间段内,甲蜡烛比乙蜡烛低?
y甲 = -15x + 30
y乙 = -10x + 25
x = 1
x>1
x<1
叁
叁
课堂小结
肆
课堂小结
肆
两个一次函数的应用
方案选择问题
实际生活中的问题
叁
肆
课后作业
基础题:1.课后习题 第 10,11题。
提高题:2.请学有余力的同学完成课后习题第12题
谢
谢
第3课时 借助两个一次函数图象解决实际问题
第四章 一次函数
4.一次函数的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
从图象中获取信息的方法:
1.弄清函数图象横、纵坐标分别表示什么,图象上最高点、最低点的意义
2.上升线表示函数值随自变量的增大而增大;下降线表示函数值随自变量的增大而减小;水平线表示函数值不随自变量的变化而变化.
3.直线倾斜程度大,表示函数值随自变量变化迅速;直线倾斜程度小,表示函数值随自变量变化缓慢.
特别提醒:一次函数图象是直线,自变量有取值范围时就变成线段或射线;k 相同则线平行
叁
叁
壹
新知初探
贰
新知初探
探究一:两个一次函数的应用
贰
引例:如图,l1 反映了某公司产品的销售收入与销售量的关系,l2 反应了该公司产品的销售成本与销售量的关系.
根据图象填空:
新知初探
贰
合作探究
(2) 当销售量为 6 t 时,
销售收入= 元,
销售成本= 元;
(1) 当销售量为 2 t 时,
销售收入= 元,
销售成本= 元;
2000
3000
6000
5000
销售量
销售收入
销售成本
新知初探
贰
(3) 当销售量等于 时,
销售收入等于销售成本;
4 t
(4) 当销售量 时,
该公司盈利(收入大于成本);
>4 t
<4 t
销售量
销售收入
销售成本
当销售量 时,
该公司亏损(收入小于成本);
直线l1与直线l2 的交点
直线l1在直线l2上方的部分
直线l1在直线l2下方的部分
从图象上看
新知初探
贰
(3) l1 对应的函数表达式是 ,
y=1000x
销售收入
销售成本
l1 的图过原点
(4,4000)
y1 = kx
4000 = 4k
k = 1000
y = 1000x
关系式设为
y1 = kx
只需要一个点的坐标
新知初探
贰
l2 对应的函数表达式是 .
y=500x+2000
l2 的图不过原点
(4,4000)
y2 = k2x + b
k2 = 500
关系式设为
y2 = kx + b
只需要两个点的坐标
(0,2000)
b = 2000
4k2+b = 4000
y=500x+2000
销售收入
销售成本
新知初探
贰
l1 对应的一次函数 y=k1x +b1中,k1 和 b1的实际意义各是什么?
想一想
k1表示每销售1吨产品,可收入1000元;
b1表示未销售时,销售收入为0元;
k2表示每销售1吨产品的成本为500元;
b2表示未销售时,为销售所花的成本为2000元;
y=1000x
l2对应的一次函数 y=k2x +b2 中,k2 和 b2 的实际意义各是什么?
y=500x+2000
新知初探
探究二:
贰
例3 图4-11是某景区游览路线示意图。甲在观景台1联系乙,发现乙在观景台2,于是沿着游览路线追赶乙。图4-12中l ,l 分别表示甲、乙两人到观景台1的路程s(单位:m)与追赶时间t(单位:min)之间的关系。
假设甲、乙两人保持现有的速度,根据图象回答下列问题:
新知初探
贰
(1)哪条线表示甲到观景台1的 路程与追赶时间之间的关系?
(2)甲和乙哪个人的速度快?
(3)30 min内甲能否追上乙?
假设甲、乙两人保持现有的速度,根据图象回答下列问题:
新知初探
贰
解:(1)当t = 0时,甲到观景台1的路程为0m,即s = 0,故l 表示甲到观景台1的路程与追赶时间之间的关系。
(2)t从0增加到20时,l1上点的纵坐标增加了1000,l2上点的纵坐标增加了600,即20 min内,甲行走了1000 m,乙行走了600 m,所以甲的速度快。
新知初探
贰
(3)如图4 - 13,延长l1,l2,可以看出,当t = 30时,l1上的对应点在l 上对应点的下方,这表明,30 min时甲尚未追上乙。
(4)在图4 - 13中,l1与l 交点P的纵坐标小于(800 + 1300 = )2100,这说明,甲能在到达观景台3前追上乙。
(5)k1表示甲的速度,k2表示乙的速度。甲的速度是50 m/min,乙的速度是30 m/min。
当堂达标
叁
当堂达标
叁
1.甲无人机从地面起飞,乙无人机从距离地面 20 m 高的楼顶起飞,两架无人机同时匀速上升 10 s.
甲、乙两架无人机所在的位置距离地面的高度 y (m) 与无人机上升的时间 x (s) 之间的关系如图所示.下列说法正确的是( )
A. 5 s时,两架无人机都上升了40 m
B. 10 s 时,两架无人机的高度差为 20 m
C. 乙无人机上升的速度为 8 m/s
D. 10 s 时,甲无人机距离地面的高度
是 60 m
B
叁
叁
当堂达标
叁
2. 如图,射线 OA、BA 分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中 s、t 分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
解析:根据图象可得出:甲的速度为
120÷5 = 24 (km/h),
乙的速度为 (120﹣4)÷5 = 23.2 (km/h),
速度差为 24 - 23.2 = 0.8 (km/h).
0.8
叁
叁
当堂达标
叁
3. 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度 y (厘米) 与燃烧时间 x (时) 之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧
前的高度分别是 ,
从点燃到燃尽所用的时间
分别是 .
30 厘米、25 厘米
2时、2.5时
叁
叁
当堂达标
叁
(2)分别求甲、乙两根蜡烛燃烧时 y 与 x 之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?
在什么时间段内,甲蜡烛比乙蜡烛高?
在什么时间段内,甲蜡烛比乙蜡烛低?
y甲 = -15x + 30
y乙 = -10x + 25
x = 1
x>1
x<1
叁
叁
课堂小结
肆
课堂小结
肆
两个一次函数的应用
方案选择问题
实际生活中的问题
叁
肆
课后作业
基础题:1.课后习题 第 10,11题。
提高题:2.请学有余力的同学完成课后习题第12题
谢
谢
同课章节目录
