5.3 第1课时 和差倍分问题 课件(共26张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 5.3 第1课时 和差倍分问题 课件(共26张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:31:56 | ||
图片预览






文档简介
(共26张PPT)
第1课时 和差倍分问题
第五章 二元一次方程组
3.应用二元一次方程组
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第 31 题“雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
叁
肆
叁
壹
情境导入
“鸡兔同笼”题为:
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何
“上有三十五头”的意思是什么
“下有九十四足”的意思是什么
你能算出鸡兔各几只吗?
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:鸡兔同笼
贰
请同学们分小组用不同的方法解决这个问题吧!
有若干只鸡兔同在一个笼子里,从上面数有 35 个头,从下面数有 94 只脚. 问笼中各有多少只鸡和兔
新知初探
贰
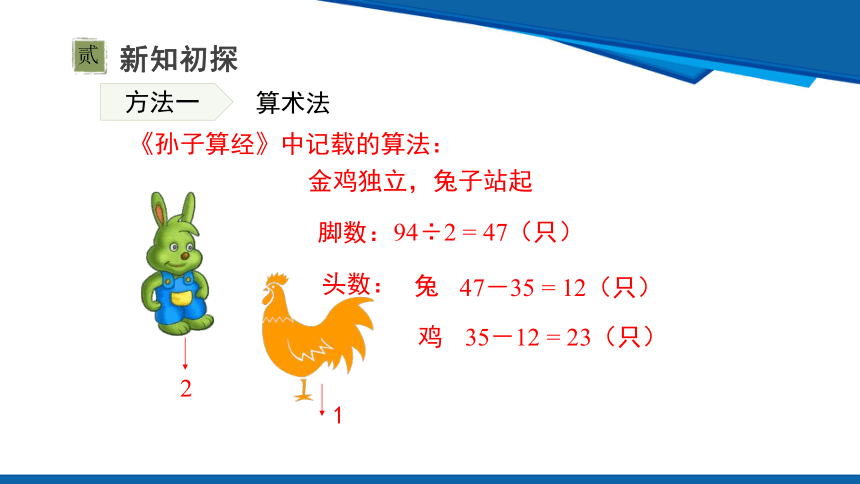
《孙子算经》中记载的算法:
金鸡独立,兔子站起
94÷2 = 47(只)
1
2
47-35 = 12(只)
脚数:
头数:
35-12 = 23(只)
兔
鸡
方法一
算术法
新知初探
贰
《孙子算经》中的算法,主要是利用了兔和鸡的脚数分别是 4 和 2,4 又是 2 的倍数. 可是当其他问题转化成这类问题时,脚数就不一定是 4 和 2,上面的计算方法就行不通.
新知初探
贰
方法二
(1) 找出,上述趣题中的等量关系;
兔的只数+鸡的只数=35;
兔的脚数+鸡的脚数=94.
设免有 x 只,则鸡有 (35-x) 只,
4x+2(35-x) = 94
(2) 适当设未知数,列出一元一次方程.
答:鸡有 23 只,兔有 12 只.
解得 x = 23
即 35-x = 12
用一元一次方程求解
新知初探
贰
设兔有 x 只,鸡有 y 只,
脚数
35
只数
合计
鸡
兔
x
y
4x
2y
94
4x+2y=94
x+y=35
方法三
用二元一次方程求解
新知初探
贰
解:设鸡为 x 只,兔为 y 只.则
①×2 得 2x + 2y = 70,③
②-③ 得 2y = 24,
y = 12.
把 y = 12 代入①,得 x = 23.
答:有鸡 23 只,兔 12 只.
x + y = 35, ①
2x + 4y = 94. ②
原方程组的解是
x = 23,
y = 12.
加减消元
新知初探
贰
解题小结:用二元一次方程组解决实际问题的步骤:
(1) 审题:弄清题意和题目中的_________;
(2) 设元:用___________表示题目中的未知数;
(3) 列方程组:根据___个等量关系列出方程组;
(4) 解方程组:利用__________法或___________解
出未知数的值;
(5) 检验并答:检验所求的解是否符合实际意义,
然后作答.
数量关系
字母
2
代入消元
加减消元法
方法总结
新知初探
探究二:和差倍分问题
贰
列方程组求解下面的问题:
若甲从乙处得到7个钱币,则甲拥有的钱币数是乙的5倍;若乙从甲处得到5个钱币,则乙拥有的钱币数是甲的7倍。甲、乙两人原来各拥有多少个钱币?(选自意大利数学家斐波那契的《计算之书》)
问题1:这个问题涉及哪些量?这些量之间有怎样的数量关系?
问题2:你能列方程解决这个问题吗?你是怎样做的?与同伴 进行交流。
新知初探
贰
例1 今有甲、乙怀钱,各不知其数。甲得乙十钱,多乙余钱五倍。乙得甲十钱,适等。问甲、乙怀钱各几何?(选自《张丘建算经》)
题目大意:甲、乙两人各带了若干钱。如果甲得到乙的10钱,那么甲钱数比乙剩余的钱数多5倍;如果乙得到甲的10钱,那么两人钱数相等。甲、乙两人各带了多少钱?
分析:题目涉及哪些数量关系?你能用含未知量的式子表示这些数量关系吗?
新知初探
贰
新知初探
贰
思考·交流
1.列二元一次方程组解决问题与列一元一次方程解决问题有什么区别和联系?与同伴进行交流。
2.类比一元一次方程解决实际问题的一般过程,请你总结归纳出运用二元一次方程组解决实际问题的步骤。
新知初探
贰
今有牛五、羊二,直金十两;牛二、羊五,直金八两.牛、羊各直金几何?
题目大意: 5 头牛、2 只羊共值 10 两“金”;2 头牛、5 只羊共值 8 两“金”. 问每头牛、每只羊各值多少“金”?
练一练
新知初探
贰
5 头牛、2 只羊共值 10 两“金”;2 头牛、5 只羊共值 8 两“金”. 问每头牛、每只羊各值多少“金”?
解: 设每头牛值“金”x 两,每只羊值“金”y 两,
由题意,得
5x + 2y = 10,
2x + 5y = 8.
解得
x = ,
y = .
{
答: 牛值“金” 两,羊值“金” 两.
当堂达标
叁
当堂达标
叁
1.《九章算术》中记载了一道数学问题,其译文为:有大小两种盛酒的桶,已知 5 个大桶加上 1 个小桶可以盛酒 3 斛(斛,音 hú,是古代一种容量单位),1 个大桶加上 5 个小桶可以盛酒 2 斛.1 个大桶、1 个小桶分别可以盛酒多少斛?设 1 个大桶可以盛酒 x 斛、1个小桶可以盛酒 y 斛.根据题意,可列方程组
______________.
叁
肆
叁
叁
当堂达标
叁
2. 《孙子算经》是中国古代重要的数学巨作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有 48 文;如果乙得到甲所有钱的 ,那么乙也共有钱 48 文,甲、乙原来各有多少钱?
解得
答:甲有 36 文,乙有 24 文.
解:设甲原有 x 文,乙原有 y 文钱.
叁
肆
叁
叁
当堂达标
叁
隔壁听到人分银,
不知人数不知银。
每人五两多六两,
每人六两少五两。
多少人数多少银?
解:设有 x 个人,y 两银,
由题意得
5x + 6 = y,
6x - 5 = y.
3. 古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得
x = 11,
y = 61.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
列方程组解决问题
一般步骤:
审、设、列、解、验、答
关键:找等量关系
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 1,2,3,4,题。
提高题:2.请学有余力的同学完成课后习题第5,6题
谢
谢
第1课时 和差倍分问题
第五章 二元一次方程组
3.应用二元一次方程组
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第 31 题“雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
叁
肆
叁
壹
情境导入
“鸡兔同笼”题为:
今有鸡兔同笼,
上有三十五头,
下有九十四足,
问鸡兔各几何
“上有三十五头”的意思是什么
“下有九十四足”的意思是什么
你能算出鸡兔各几只吗?
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:鸡兔同笼
贰
请同学们分小组用不同的方法解决这个问题吧!
有若干只鸡兔同在一个笼子里,从上面数有 35 个头,从下面数有 94 只脚. 问笼中各有多少只鸡和兔
新知初探
贰
《孙子算经》中记载的算法:
金鸡独立,兔子站起
94÷2 = 47(只)
1
2
47-35 = 12(只)
脚数:
头数:
35-12 = 23(只)
兔
鸡
方法一
算术法
新知初探
贰
《孙子算经》中的算法,主要是利用了兔和鸡的脚数分别是 4 和 2,4 又是 2 的倍数. 可是当其他问题转化成这类问题时,脚数就不一定是 4 和 2,上面的计算方法就行不通.
新知初探
贰
方法二
(1) 找出,上述趣题中的等量关系;
兔的只数+鸡的只数=35;
兔的脚数+鸡的脚数=94.
设免有 x 只,则鸡有 (35-x) 只,
4x+2(35-x) = 94
(2) 适当设未知数,列出一元一次方程.
答:鸡有 23 只,兔有 12 只.
解得 x = 23
即 35-x = 12
用一元一次方程求解
新知初探
贰
设兔有 x 只,鸡有 y 只,
脚数
35
只数
合计
鸡
兔
x
y
4x
2y
94
4x+2y=94
x+y=35
方法三
用二元一次方程求解
新知初探
贰
解:设鸡为 x 只,兔为 y 只.则
①×2 得 2x + 2y = 70,③
②-③ 得 2y = 24,
y = 12.
把 y = 12 代入①,得 x = 23.
答:有鸡 23 只,兔 12 只.
x + y = 35, ①
2x + 4y = 94. ②
原方程组的解是
x = 23,
y = 12.
加减消元
新知初探
贰
解题小结:用二元一次方程组解决实际问题的步骤:
(1) 审题:弄清题意和题目中的_________;
(2) 设元:用___________表示题目中的未知数;
(3) 列方程组:根据___个等量关系列出方程组;
(4) 解方程组:利用__________法或___________解
出未知数的值;
(5) 检验并答:检验所求的解是否符合实际意义,
然后作答.
数量关系
字母
2
代入消元
加减消元法
方法总结
新知初探
探究二:和差倍分问题
贰
列方程组求解下面的问题:
若甲从乙处得到7个钱币,则甲拥有的钱币数是乙的5倍;若乙从甲处得到5个钱币,则乙拥有的钱币数是甲的7倍。甲、乙两人原来各拥有多少个钱币?(选自意大利数学家斐波那契的《计算之书》)
问题1:这个问题涉及哪些量?这些量之间有怎样的数量关系?
问题2:你能列方程解决这个问题吗?你是怎样做的?与同伴 进行交流。
新知初探
贰
例1 今有甲、乙怀钱,各不知其数。甲得乙十钱,多乙余钱五倍。乙得甲十钱,适等。问甲、乙怀钱各几何?(选自《张丘建算经》)
题目大意:甲、乙两人各带了若干钱。如果甲得到乙的10钱,那么甲钱数比乙剩余的钱数多5倍;如果乙得到甲的10钱,那么两人钱数相等。甲、乙两人各带了多少钱?
分析:题目涉及哪些数量关系?你能用含未知量的式子表示这些数量关系吗?
新知初探
贰
新知初探
贰
思考·交流
1.列二元一次方程组解决问题与列一元一次方程解决问题有什么区别和联系?与同伴进行交流。
2.类比一元一次方程解决实际问题的一般过程,请你总结归纳出运用二元一次方程组解决实际问题的步骤。
新知初探
贰
今有牛五、羊二,直金十两;牛二、羊五,直金八两.牛、羊各直金几何?
题目大意: 5 头牛、2 只羊共值 10 两“金”;2 头牛、5 只羊共值 8 两“金”. 问每头牛、每只羊各值多少“金”?
练一练
新知初探
贰
5 头牛、2 只羊共值 10 两“金”;2 头牛、5 只羊共值 8 两“金”. 问每头牛、每只羊各值多少“金”?
解: 设每头牛值“金”x 两,每只羊值“金”y 两,
由题意,得
5x + 2y = 10,
2x + 5y = 8.
解得
x = ,
y = .
{
答: 牛值“金” 两,羊值“金” 两.
当堂达标
叁
当堂达标
叁
1.《九章算术》中记载了一道数学问题,其译文为:有大小两种盛酒的桶,已知 5 个大桶加上 1 个小桶可以盛酒 3 斛(斛,音 hú,是古代一种容量单位),1 个大桶加上 5 个小桶可以盛酒 2 斛.1 个大桶、1 个小桶分别可以盛酒多少斛?设 1 个大桶可以盛酒 x 斛、1个小桶可以盛酒 y 斛.根据题意,可列方程组
______________.
叁
肆
叁
叁
当堂达标
叁
2. 《孙子算经》是中国古代重要的数学巨作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有 48 文;如果乙得到甲所有钱的 ,那么乙也共有钱 48 文,甲、乙原来各有多少钱?
解得
答:甲有 36 文,乙有 24 文.
解:设甲原有 x 文,乙原有 y 文钱.
叁
肆
叁
叁
当堂达标
叁
隔壁听到人分银,
不知人数不知银。
每人五两多六两,
每人六两少五两。
多少人数多少银?
解:设有 x 个人,y 两银,
由题意得
5x + 6 = y,
6x - 5 = y.
3. 古有一捕快,一天晚上他在野外的一个茅屋里,听到外边来了一群人在吵闹,他隐隐约约地听到几个声音,下面有这一古诗为证:
解得
x = 11,
y = 61.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
列方程组解决问题
一般步骤:
审、设、列、解、验、答
关键:找等量关系
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 1,2,3,4,题。
提高题:2.请学有余力的同学完成课后习题第5,6题
谢
谢
同课章节目录
