5.3 第2课时 借助表格解决实际问题 课件(共25张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 5.3 第2课时 借助表格解决实际问题 课件(共25张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第2课时 借助表格解决实际问题
第五章 二元一次方程组
3.应用二元一次方程组
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
新年来临爸爸想送小明一个书包和学习机作为新年礼物.爸爸对小明说:“我在甲、乙两个商场都发现同款的学习机的单价相同,书包单价也相同,学习机和书包单价之和是1072元,且学习机的单价比书包单价的8倍少8元,你能说出学习机和书包单价各是多少元,那么我就买给你做新年礼物”。你能帮助他吗?
叁
肆
叁
壹
新知初探
贰
新知初探
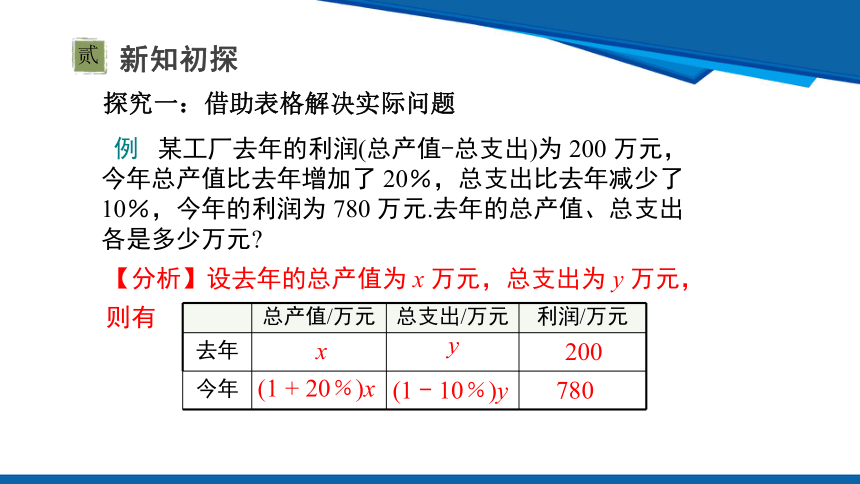
探究一:借助表格解决实际问题
贰
【分析】设去年的总产值为 x 万元,总支出为 y 万元,则有
总产值/万元 总支出/万元 利润/万元
去年
今年
(1 + 20﹪)x
(1 - 10﹪)y
780
x
y
200
例 某工厂去年的利润(总产值-总支出)为 200 万元,今年总产值比去年增加了 20%,总支出比去年减少了 10%,今年的利润为 780 万元.去年的总产值、总支出各是多少万元
新知初探
贰
去年的总产值 - 去年的总支出 = 200 万元,
今年的总产值 - 今年的总支出 = 780 万元 .
分析
关键:找出等量关系.
今年的总产值=
去年总产值×(1 + 20%)
今年的总支出=去年的总支出×(1 - 10%)
新知初探
贰
解:设去年的总产值为 x 万元,总支出为 y 万元,则有
x - y = 200
(1 + 20﹪)x - (1 - 10﹪)y = 780
因此,去年的总产值是 2000 万元,总支出是 1800万元.
解得
x = 2000
y = 1800
新知初探
贰
1. 甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价 15%,乙商品提价 10%,调价后两种商品的单价和比原来的单价和降低了 5%.
求甲、乙两种商品原来的单价.
本问题涉及的等量关系为:
甲商品原单价十乙商品原单价 = 100元,
调价后甲商品单价+调价后乙商品单价=100×(1-5%)元.
x
y
x - 15%x = (1-15%)x
x + 10%x = (1+10%)x
随堂练习
新知初探
贰
解:设甲商品原来的单价为 x 元,乙商品原来的单价为 y 元.
根据题意,得
答:甲、乙商品原来的单价分别为 60 元,40 元.
x+y=100,
(1-15%)x+(1+10%)y=100×(1-5%).
解得
x=60,
y=40.
新知初探
探究二:典例精析
贰
例2 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含 0.5 单位蛋白质和 1 单位铁质,每克乙原料含 0.7 单位蛋白质和 0.4 单位铁质,若病人每餐需要 35 单位蛋白质和 40 单位铁质,那么每餐甲、乙原料各多少克恰好满足病人的需要
解:设每餐甲、乙原料各 x g、y g. 则有下表:
甲原料x g 乙原料y g 所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
新知初探
贰
①- ②,得 5y = 150
y = 30
所以每餐需甲原料 28 g,乙原料 30 g.
根据题意,得方程组
0.5x + 0.7y = 35
x + 0.4y = 40
5x + 7y = 350 ①
5x + 2y = 200 ②
化简,得
把 y = 30 代入①,得 x = 28,即方程组的解为:
新知初探
贰
2.如图,长青化工厂与 A,B 两地有公路、铁路相连,这家工厂从 A 地购买一批每吨 1 000 元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地. 已知公路运价为 1.5 元/(t · km),铁路运价为 1.2 元/(t · km),这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元,这批产品的销售款比原料费
与运输费的和多多少元?
随堂练习
新知初探
贰
产品 x 吨 原料 y 吨 合 计
公路运费(元)
铁路运费(元)
价值(元)
借助列表分析,确定题目中的数量关系.
1.5×20x
1.2×110x
8000x
1.5×10y
1.2×120y
1000y
15 000
97 200
本问题涉及的等量关系为:
产品数量×产品价格=销售款,
原料数量×原料价格=原料费,
运输价格×运价=运输费
新知初探
贰
解:根据图表,列出方程组
解方程组得
x = 300,
y = 400.
8 000x - 1 000y - 15 000 - 97 200
= 8000×300 - 1 000×400 - 15 000 - 97 200
= 1 887 800(元).
答:这批产品的销售款比原料费与运输费的和多 1 887 800 元.
1.5×20x + 1.5×10y = 15 000,
1.2×110x + 1.2×120y = 97 200.
新知初探
贰
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
归纳总结
当堂达标
叁
当堂达标
叁
1. 某校春季运动会比赛中,八年级 (1) 班、(5) 班的竞技实力相当,关于比赛结果,甲同学说:(1) 班与 (5) 班得分比为 6:5;乙同学说:(1) 班得分比 (5) 班得分的 2 倍少 40 分.若设 (1) 班得 x 分,(5) 班得 y 分,根据题意所列的方程组应为( )
B.
C.
D.
A.
D
叁
肆
叁
叁
当堂达标
叁
2.有甲乙两种溶液,甲种溶液由酒精 1 升,水 3 升配制而成;乙种溶液由酒精 3 升,水 2 升配制而成.现要配制浓度为 50% 的酒精溶液 7 升,甲乙两种溶液应各取几升
解:设甲种溶液需 x 升,乙种溶液需 y 升,
则有
x + y = 7,
25%x + 60%y = 50%×7.
解得
y = 5.
x = 2,
答:甲种溶液应取 2 升,乙种溶液应取 5 升.
叁
肆
叁
叁
当堂达标
叁
3.某人以两种形式存 8000 元,一种储蓄的年利率为10%,另一种储蓄的年利率为 11%. 一年到期后,他共得利息 855 元 (没有利息税),问两种储蓄他各存了多少钱
解:设年利率为 11% 的存 x 元,年利率 10% 存 y 元.
则
x + y = 8000,
11%x + 10%y = 855.
x = 5500,
y = 2500.
解得
答:年利率为 11% 的存 5500 元,年利率 10% 存 2500 元.
叁
肆
叁
叁
当堂达标
叁
4.甲、乙两人从相距 36 千米的两地相向而行,如甲比乙先走 2 小时,那么他们在乙出发 2.5 小时后相遇;如果乙比甲先走 2 小时,那么他们在甲出发 3 小时后相遇,甲、乙两人每时各走多少千米
分析:设甲、乙两人每小时分别行走 x 千米,y 千米. 填写下表并求出 x,y 的值.
叁
肆
叁
叁
当堂达标
叁
甲行走的路程 乙行走的路程 甲乙行走的路程和
甲先走 2 小时
乙先走 2 小时
(2 + 2.5)x
2.5y
36
36
3x
(2 + 3)y
解得
x = 6,
y = 3.6.
(2 + 2.5)x + 2.5y = 36,
3x + (2 + 3)y = 36.
解:设甲、乙两人每小时分别行走 x 千米,y 千米.
由题意,得
答:甲每时走 6 千米,乙每时走 3.6 千米.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
列方程组解决实际问题
增长率、利润问题
利用图表分析等量关系
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 7,8,9题。
提高题:2.请学有余力的同学完成课后习题第10题
谢
谢
第2课时 借助表格解决实际问题
第五章 二元一次方程组
3.应用二元一次方程组
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
新年来临爸爸想送小明一个书包和学习机作为新年礼物.爸爸对小明说:“我在甲、乙两个商场都发现同款的学习机的单价相同,书包单价也相同,学习机和书包单价之和是1072元,且学习机的单价比书包单价的8倍少8元,你能说出学习机和书包单价各是多少元,那么我就买给你做新年礼物”。你能帮助他吗?
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:借助表格解决实际问题
贰
【分析】设去年的总产值为 x 万元,总支出为 y 万元,则有
总产值/万元 总支出/万元 利润/万元
去年
今年
(1 + 20﹪)x
(1 - 10﹪)y
780
x
y
200
例 某工厂去年的利润(总产值-总支出)为 200 万元,今年总产值比去年增加了 20%,总支出比去年减少了 10%,今年的利润为 780 万元.去年的总产值、总支出各是多少万元
新知初探
贰
去年的总产值 - 去年的总支出 = 200 万元,
今年的总产值 - 今年的总支出 = 780 万元 .
分析
关键:找出等量关系.
今年的总产值=
去年总产值×(1 + 20%)
今年的总支出=去年的总支出×(1 - 10%)
新知初探
贰
解:设去年的总产值为 x 万元,总支出为 y 万元,则有
x - y = 200
(1 + 20﹪)x - (1 - 10﹪)y = 780
因此,去年的总产值是 2000 万元,总支出是 1800万元.
解得
x = 2000
y = 1800
新知初探
贰
1. 甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价 15%,乙商品提价 10%,调价后两种商品的单价和比原来的单价和降低了 5%.
求甲、乙两种商品原来的单价.
本问题涉及的等量关系为:
甲商品原单价十乙商品原单价 = 100元,
调价后甲商品单价+调价后乙商品单价=100×(1-5%)元.
x
y
x - 15%x = (1-15%)x
x + 10%x = (1+10%)x
随堂练习
新知初探
贰
解:设甲商品原来的单价为 x 元,乙商品原来的单价为 y 元.
根据题意,得
答:甲、乙商品原来的单价分别为 60 元,40 元.
x+y=100,
(1-15%)x+(1+10%)y=100×(1-5%).
解得
x=60,
y=40.
新知初探
探究二:典例精析
贰
例2 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含 0.5 单位蛋白质和 1 单位铁质,每克乙原料含 0.7 单位蛋白质和 0.4 单位铁质,若病人每餐需要 35 单位蛋白质和 40 单位铁质,那么每餐甲、乙原料各多少克恰好满足病人的需要
解:设每餐甲、乙原料各 x g、y g. 则有下表:
甲原料x g 乙原料y g 所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
新知初探
贰
①- ②,得 5y = 150
y = 30
所以每餐需甲原料 28 g,乙原料 30 g.
根据题意,得方程组
0.5x + 0.7y = 35
x + 0.4y = 40
5x + 7y = 350 ①
5x + 2y = 200 ②
化简,得
把 y = 30 代入①,得 x = 28,即方程组的解为:
新知初探
贰
2.如图,长青化工厂与 A,B 两地有公路、铁路相连,这家工厂从 A 地购买一批每吨 1 000 元的原料运回工厂,制成每吨 8 000 元的产品运到 B 地. 已知公路运价为 1.5 元/(t · km),铁路运价为 1.2 元/(t · km),这两次运输共支出公路运费 15 000 元,铁路运费 97 200 元,这批产品的销售款比原料费
与运输费的和多多少元?
随堂练习
新知初探
贰
产品 x 吨 原料 y 吨 合 计
公路运费(元)
铁路运费(元)
价值(元)
借助列表分析,确定题目中的数量关系.
1.5×20x
1.2×110x
8000x
1.5×10y
1.2×120y
1000y
15 000
97 200
本问题涉及的等量关系为:
产品数量×产品价格=销售款,
原料数量×原料价格=原料费,
运输价格×运价=运输费
新知初探
贰
解:根据图表,列出方程组
解方程组得
x = 300,
y = 400.
8 000x - 1 000y - 15 000 - 97 200
= 8000×300 - 1 000×400 - 15 000 - 97 200
= 1 887 800(元).
答:这批产品的销售款比原料费与运输费的和多 1 887 800 元.
1.5×20x + 1.5×10y = 15 000,
1.2×110x + 1.2×120y = 97 200.
新知初探
贰
实际问题
设未知数、找等量关系、列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
归纳总结
当堂达标
叁
当堂达标
叁
1. 某校春季运动会比赛中,八年级 (1) 班、(5) 班的竞技实力相当,关于比赛结果,甲同学说:(1) 班与 (5) 班得分比为 6:5;乙同学说:(1) 班得分比 (5) 班得分的 2 倍少 40 分.若设 (1) 班得 x 分,(5) 班得 y 分,根据题意所列的方程组应为( )
B.
C.
D.
A.
D
叁
肆
叁
叁
当堂达标
叁
2.有甲乙两种溶液,甲种溶液由酒精 1 升,水 3 升配制而成;乙种溶液由酒精 3 升,水 2 升配制而成.现要配制浓度为 50% 的酒精溶液 7 升,甲乙两种溶液应各取几升
解:设甲种溶液需 x 升,乙种溶液需 y 升,
则有
x + y = 7,
25%x + 60%y = 50%×7.
解得
y = 5.
x = 2,
答:甲种溶液应取 2 升,乙种溶液应取 5 升.
叁
肆
叁
叁
当堂达标
叁
3.某人以两种形式存 8000 元,一种储蓄的年利率为10%,另一种储蓄的年利率为 11%. 一年到期后,他共得利息 855 元 (没有利息税),问两种储蓄他各存了多少钱
解:设年利率为 11% 的存 x 元,年利率 10% 存 y 元.
则
x + y = 8000,
11%x + 10%y = 855.
x = 5500,
y = 2500.
解得
答:年利率为 11% 的存 5500 元,年利率 10% 存 2500 元.
叁
肆
叁
叁
当堂达标
叁
4.甲、乙两人从相距 36 千米的两地相向而行,如甲比乙先走 2 小时,那么他们在乙出发 2.5 小时后相遇;如果乙比甲先走 2 小时,那么他们在甲出发 3 小时后相遇,甲、乙两人每时各走多少千米
分析:设甲、乙两人每小时分别行走 x 千米,y 千米. 填写下表并求出 x,y 的值.
叁
肆
叁
叁
当堂达标
叁
甲行走的路程 乙行走的路程 甲乙行走的路程和
甲先走 2 小时
乙先走 2 小时
(2 + 2.5)x
2.5y
36
36
3x
(2 + 3)y
解得
x = 6,
y = 3.6.
(2 + 2.5)x + 2.5y = 36,
3x + (2 + 3)y = 36.
解:设甲、乙两人每小时分别行走 x 千米,y 千米.
由题意,得
答:甲每时走 6 千米,乙每时走 3.6 千米.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
列方程组解决实际问题
增长率、利润问题
利用图表分析等量关系
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 7,8,9题。
提高题:2.请学有余力的同学完成课后习题第10题
谢
谢
同课章节目录
