5.4 第2课时 用二元一次方程组确定一次函数表达式 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 5.4 第2课时 用二元一次方程组确定一次函数表达式 课件(共23张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:34:17 | ||
图片预览








文档简介
(共23张PPT)
第2课时 用二元一次方程组确定一次函数表达式
第五章 二元一次方程组
4.二元一次方程与一次函数
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
1. 二元一次方程组与一次函数有何联系
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点坐标也是它们所对应的二元一次方程组的解.
2. 二元一次方程组有哪些解法?
消元法
图象法
是一种代数方法
温故知新:
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:用二元一次方程确定一次函数表达式
贰
议一议:A,B 两地相距 100 千米,甲、乙两人骑车同时分别从 A,B 两地相向而行.假设他们都保持匀速行驶,则他们各自到 A 地的距离 s (千米)都是骑车时间 t (时)的一次函数. 1 小时后乙距 A 地 80 千米;2 小时后甲距 A 地30 千米. 问:经过多长时间两人相遇 说出你的方法,并与同学们交流.
1 小时后
2 小时后甲距A地 30 千米
乙距 A 地 80 千米
A
B
乙
甲
新知初探
贰
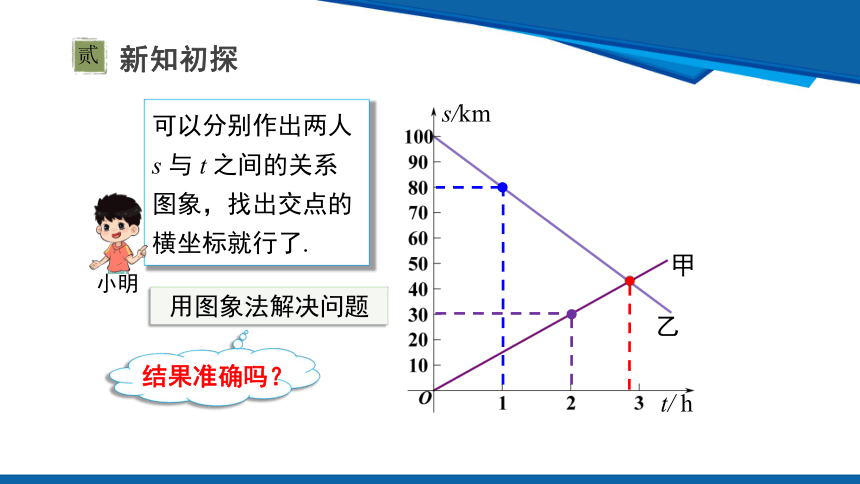
可以分别作出两人 s 与 t 之间的关系图象,找出交点的横坐标就行了.
s/km
t/ h
甲
乙
小明
用图象法解决问题
结果准确吗?
新知初探
贰
设同时出发后 t 小时相遇,则 (15 + 20)t = 100
用一元一次方程的方法解决问题
1 小时后
2 小时后甲距A地 30 千米
乙距 A 地 80 千米
A
B
乙
甲
1 时后乙距 A 地 80 千米,即乙的速度是 20 千米/时
2 时后甲距 A 地 30 千米,故甲的速度是 15 千米/时
小颖
新知初探
贰
对于乙,s 是 t 的一次函数,可设 s = k1t + b1.
当 t = 0 时,s = 100;当 t = 1 时,s = 80.
将它们分别代入 s = k1t + b1 中,
b1=100,
k1+b1=80
①
②
b1=100
k1=-20,
解得
对于甲,s 是 t 的正比例函数,可设 s = k2t .
当 t = 2 时,s = 30,代入 s = k2t 中,
2k2=30
k2=15
s = -20t + 100
s = 15t
小亮
新知初探
贰
s = -20t + 100,
s = 15t
联立
解得
用二元一次方程组的方法确定一次函数表达式
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.
新知初探
探究二:典例精析
贰
例 某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费 y (元) 是行李质量 x (kg) 的一次函数.已知李明带了 60 kg 的行李,交了行李费 5 元;张华带了 90 kg 的行李,交了行李费 10 元.
(1) 写出 y 与 x 之间的函数表达式;
(2) 旅客最多可免费携带多少千克的行李?
新知初探
贰
解:(1) 设 y = kx + b (k≠0),根据题意,得
所以旅客最多可免费携带 30 千克的行李.
②-①,得 30k = 5,
将 代入①,得 b = -5.
所以
(2) 令 y = 0, ,解得 x = 30 ;
当 x>30 时,y>0.
新知初探
贰
像这样,先设出函数表达式,再根据所给条件确定表达式中未知的系数,从而得到函数表达式的方法,叫作待定系数法.
知识要点
新知初探
贰
y = kx + b (k ≠ 0)
二元一次
归纳总结
(1)设:设一次函数的一般形式 ; (2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的表达式,组成_________方程组;
(3)解:解二元一次方程组得 k,b;
(4)还原:把 k,b 的值代入一次函数的表达式.
求一次函数表达式的步骤:
新知初探
贰
随堂练习
1. 已知一个正比例函数的图象经过点 (-2,4),则这个正比例函数的表达式是 ________.
2. 已知一次函数 y = kx + 5 的图象经过点 (-1,2),则
k =______.
3. 已知函数 y = 2x + b 的图像经过点 (a,7) 和 (-2,a),则这个函数的表达式为____________.
y = -2x
3
y = 2x + 5
新知初探
贰
解方程组得
b = -1.
4. 已知一次函数的图象过点(3,5)与(-4,-9),
求这个一次函数的表达式.
解:设这个一次函数的表达式为 y = kx + b.
3k + b = 5,
-4k + b = -9,
所以这个一次函数的表达式为
把点(3,5)与(-4,-9)分别代入,得:
k = 2,
y = 2x - 1.
当堂达标
叁
当堂达标
叁
1. 如图,直线 l 是一次函数 y = kx + b 的图象,填空:
(1)b =______,k =______;
(2)当 x = 30 时,y =______;
(3)当 y = 30 时,x =______.
2
-18
-42
l
叁
肆
叁
叁
当堂达标
叁
2. 判断三点 A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
解:设过 A,B 两点的直线的表达式为
y = kx + b,由题意可知,
所以过 A,B 两点的直线的表达式为 y = x - 2.
因为当 x = 4 时,y = 4 - 2 = 2.
所以点 C(4,2)在直线 y = x - 2上.
所以三点 A(3,1), B(0,-2),C(4,2)
在同一条直线上.
解得
叁
肆
叁
叁
当堂达标
叁
3.在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少
解:设购买量 y 与单价 x 的函数表达式为 y = kx + b,
因为当 x = 1000 时 y = 800;当 x = 2000 时 y = 700,
所以
800k + b = 1000
700k + b = 2000
{
解得
b = 9000
因此,购买量 y 与单价 x 的函数表达式为 y = -10x + 9000
当 y = 400 时,-10x + 9000 = 400,
∴ x = 860.
答:当客户购买 400 kg,单价是 860 元.
{
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
利用二元一次方程确定一次函数表达式
用含字母的系数设出一次函数的表达式:
y = kx + b
将已知条件代入上述表达式中得关于 k,b的二元一次方程组
解这个二元一次方程组得 k,b
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 5,6题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
第2课时 用二元一次方程组确定一次函数表达式
第五章 二元一次方程组
4.二元一次方程与一次函数
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
1. 二元一次方程组与一次函数有何联系
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点坐标也是它们所对应的二元一次方程组的解.
2. 二元一次方程组有哪些解法?
消元法
图象法
是一种代数方法
温故知新:
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:用二元一次方程确定一次函数表达式
贰
议一议:A,B 两地相距 100 千米,甲、乙两人骑车同时分别从 A,B 两地相向而行.假设他们都保持匀速行驶,则他们各自到 A 地的距离 s (千米)都是骑车时间 t (时)的一次函数. 1 小时后乙距 A 地 80 千米;2 小时后甲距 A 地30 千米. 问:经过多长时间两人相遇 说出你的方法,并与同学们交流.
1 小时后
2 小时后甲距A地 30 千米
乙距 A 地 80 千米
A
B
乙
甲
新知初探
贰
可以分别作出两人 s 与 t 之间的关系图象,找出交点的横坐标就行了.
s/km
t/ h
甲
乙
小明
用图象法解决问题
结果准确吗?
新知初探
贰
设同时出发后 t 小时相遇,则 (15 + 20)t = 100
用一元一次方程的方法解决问题
1 小时后
2 小时后甲距A地 30 千米
乙距 A 地 80 千米
A
B
乙
甲
1 时后乙距 A 地 80 千米,即乙的速度是 20 千米/时
2 时后甲距 A 地 30 千米,故甲的速度是 15 千米/时
小颖
新知初探
贰
对于乙,s 是 t 的一次函数,可设 s = k1t + b1.
当 t = 0 时,s = 100;当 t = 1 时,s = 80.
将它们分别代入 s = k1t + b1 中,
b1=100,
k1+b1=80
①
②
b1=100
k1=-20,
解得
对于甲,s 是 t 的正比例函数,可设 s = k2t .
当 t = 2 时,s = 30,代入 s = k2t 中,
2k2=30
k2=15
s = -20t + 100
s = 15t
小亮
新知初探
贰
s = -20t + 100,
s = 15t
联立
解得
用二元一次方程组的方法确定一次函数表达式
用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.
新知初探
探究二:典例精析
贰
例 某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费 y (元) 是行李质量 x (kg) 的一次函数.已知李明带了 60 kg 的行李,交了行李费 5 元;张华带了 90 kg 的行李,交了行李费 10 元.
(1) 写出 y 与 x 之间的函数表达式;
(2) 旅客最多可免费携带多少千克的行李?
新知初探
贰
解:(1) 设 y = kx + b (k≠0),根据题意,得
所以旅客最多可免费携带 30 千克的行李.
②-①,得 30k = 5,
将 代入①,得 b = -5.
所以
(2) 令 y = 0, ,解得 x = 30 ;
当 x>30 时,y>0.
新知初探
贰
像这样,先设出函数表达式,再根据所给条件确定表达式中未知的系数,从而得到函数表达式的方法,叫作待定系数法.
知识要点
新知初探
贰
y = kx + b (k ≠ 0)
二元一次
归纳总结
(1)设:设一次函数的一般形式 ; (2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的表达式,组成_________方程组;
(3)解:解二元一次方程组得 k,b;
(4)还原:把 k,b 的值代入一次函数的表达式.
求一次函数表达式的步骤:
新知初探
贰
随堂练习
1. 已知一个正比例函数的图象经过点 (-2,4),则这个正比例函数的表达式是 ________.
2. 已知一次函数 y = kx + 5 的图象经过点 (-1,2),则
k =______.
3. 已知函数 y = 2x + b 的图像经过点 (a,7) 和 (-2,a),则这个函数的表达式为____________.
y = -2x
3
y = 2x + 5
新知初探
贰
解方程组得
b = -1.
4. 已知一次函数的图象过点(3,5)与(-4,-9),
求这个一次函数的表达式.
解:设这个一次函数的表达式为 y = kx + b.
3k + b = 5,
-4k + b = -9,
所以这个一次函数的表达式为
把点(3,5)与(-4,-9)分别代入,得:
k = 2,
y = 2x - 1.
当堂达标
叁
当堂达标
叁
1. 如图,直线 l 是一次函数 y = kx + b 的图象,填空:
(1)b =______,k =______;
(2)当 x = 30 时,y =______;
(3)当 y = 30 时,x =______.
2
-18
-42
l
叁
肆
叁
叁
当堂达标
叁
2. 判断三点 A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
解:设过 A,B 两点的直线的表达式为
y = kx + b,由题意可知,
所以过 A,B 两点的直线的表达式为 y = x - 2.
因为当 x = 4 时,y = 4 - 2 = 2.
所以点 C(4,2)在直线 y = x - 2上.
所以三点 A(3,1), B(0,-2),C(4,2)
在同一条直线上.
解得
叁
肆
叁
叁
当堂达标
叁
3.在某个范围内,某产品的购买量y(单位:kg)与单价x(单位:元)之间满足一次函数,若购买1000kg,单价为800元;若购买2000kg,单价为700元.若一客户购买400kg,单价是多少
解:设购买量 y 与单价 x 的函数表达式为 y = kx + b,
因为当 x = 1000 时 y = 800;当 x = 2000 时 y = 700,
所以
800k + b = 1000
700k + b = 2000
{
解得
b = 9000
因此,购买量 y 与单价 x 的函数表达式为 y = -10x + 9000
当 y = 400 时,-10x + 9000 = 400,
∴ x = 860.
答:当客户购买 400 kg,单价是 860 元.
{
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
利用二元一次方程确定一次函数表达式
用含字母的系数设出一次函数的表达式:
y = kx + b
将已知条件代入上述表达式中得关于 k,b的二元一次方程组
解这个二元一次方程组得 k,b
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 5,6题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
同课章节目录
