问题解决策略:反思 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 问题解决策略:反思 课件(共24张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:35:07 | ||
图片预览







文档简介
(共24张PPT)
第一章 勾股定理
问题解决策略:反思
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
看图片,引出问题:有一块长方形绿地,绿地周边是小路,在绿地旁边的B处有健身器材.居住在A处的居民在看到牌子上“禁止踩踏花草,文明步行”后,为了走近路而不惜践踏草地直接从A到B.各位同学,你知道他们为什么不走绿地周边的路吗?
新知初探
贰
新知初探
探究一:路径最短问题
贰
A
B
问题:如图,有一个圆柱,它的高等于12cm,底面圆的周长为18cm,在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?
新知初探
贰
新知初探
贰
活动1 理解问题
(1)在这个问题中,已知条件有哪些?你认为已知条件足够解决这个问题吗?
(2)沿侧面爬行的可能路线有哪些?什么情况下路线最短?请你用图形水杯等物品实际感受一下。
新知初探
贰
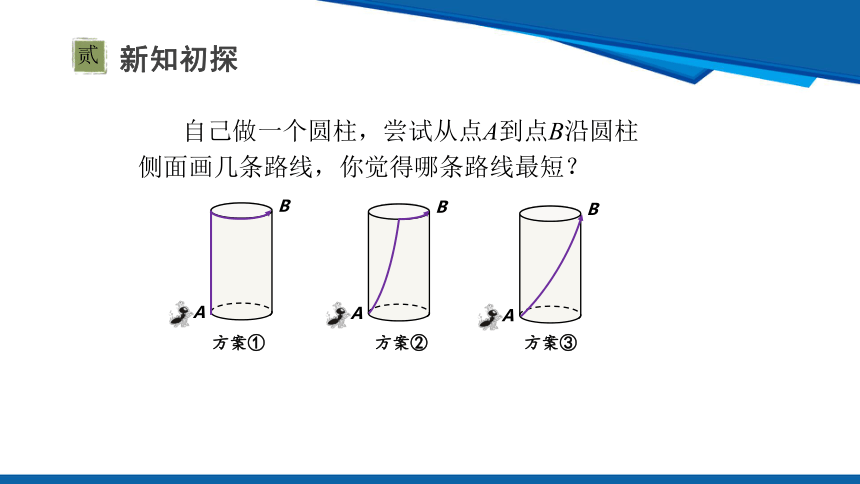
自己做一个圆柱,尝试从点A到点B沿圆柱侧面画几条路线,你觉得哪条路线最短?
A
B
A
B
A
B
方案①
方案②
方案③
新知初探
贰
活动2 拟定计划
(1)以前研究过最短路线问题吗?这个问题与以前研究的最短路线问题有什么不同?
(2)如何将曲面最短路线问题转化为平面上的最短路线问题?各个点的位置如何确定?
新知初探
贰
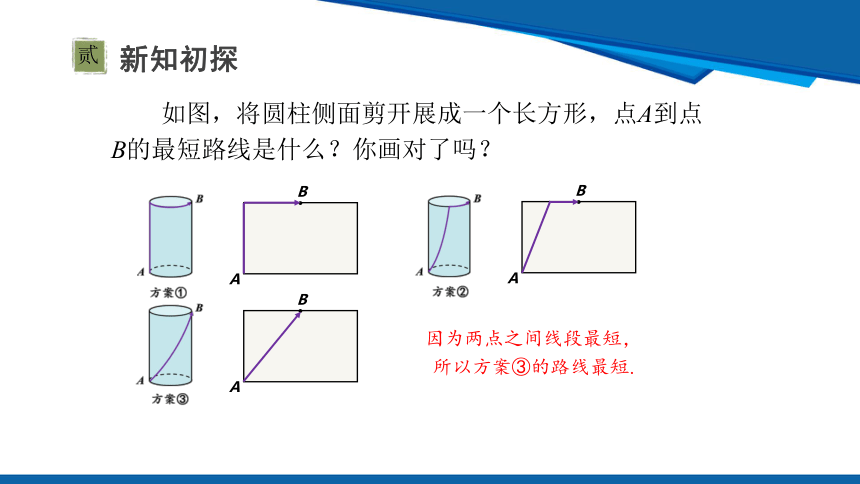
如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?你画对了吗?
A
B
A
B
A
B
因为两点之间线段最短,
所以方案③的路线最短.
新知初探
贰
活动3 实施计划
(1)如图,将圆柱侧面剪开,确定展开图的形状,以及与圆柱的对应关系。
(3)在图中确定A,B两点之间最短的路线,并计算它的长度。
(2)在图中标出点B的位置。
新知初探
贰
蚂蚁从点A出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?
在Rt△ABC中,
AC=12cm,BC=18÷2=9(cm).
由勾股定理,得
AB2=AC2+BC2
=122+92
=225.
所以最短路程AB=15cm.
A
B
C
高12cm,底面周长18cm.
新知初探
贰
活动4 回顾反思
(1)在拟订解决问题的方案和实施方案的过程中,你获得了哪些经验 与同伴进行交流。
(2)从这个问题中,影响结果的量有哪些 如果改变有关的量,你还能求解吗?例如,改变圆柱的形状,改变A,B两点的位置,改为沿着圆柱表面爬……这时又会有哪些新的问题 选择部分问题进行研究,并与同伴进行交流。
新知初探
贰
(4)生活中还有哪些现实问题涉及几何体表面上的最短距离 举几个实例,并思考解决问题的方案。
(5)对于解决问题之后的回顾反思,你有哪些体会 与同伴进行交流。
(3)解决这个问题的经验,还可以运用到哪些问题中 例如,能否解决正方体、长方体等几何体表面两点之间的最短距离问题
新知初探
贰
活动5 变式训练
如图,一只蜘蛛在一个长方体木块
的顶点A处,一只苍蝇在这个长方体
木块的顶点G处,若AB=3 cm,BC=5 cm,
BF=6 cm,问蜘蛛要沿着怎样的路线爬
行,才能最快抓到苍蝇?这时蜘蛛走
过的路程是多少?
新知初探
贰
解:如图,根据题意,得A点到G点的路线有以上三种情况:
AG2=AF2+GF2=92+52=106
AG2=AB2+BG2=32+112=130
AG2=AC2+CG2=82+62=100。
综上,蜘蛛走过的路程是10 cm。
新知初探
贰
解决问题之后的反思,一般可以关注以下几个方面,反思解决问题的过程,强化解决问题的经验,比较解决问题的方法,形成多样的解决问题的方法,思考方法的本质,促进方法的运用,改变问题的条件,研究更多的问题。
活动6 小结
当堂达标
叁
当堂达标
叁
1.如图,已知圆柱的底面周长为10cm,高AB为12cm,BC是底面的直径,一只蚂蚁沿着圆柱侧面爬行觅食从点C爬到点A,则蚂蚁爬行的最短路线为 cm.
13
叁
当堂达标
叁
2.如图,一个三级台阶,它的每一级的长、宽和高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的点,A点处有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶爬到B点,至少需爬( )
A.13 cm B.40 cm
C.130 cm D.169 cm
C
叁
当堂达标
叁
3.如图,长方体的透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼铒,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内到G处吃鱼铒,则小虫爬行的最短路线长为( )
A.40 cm B.60 cm
C.80 cm D.100 cm
D
叁
课堂小结
肆
课堂小结
肆
勾股定理的应用
解决图形中路线最短的问题关键
应用勾股定理解决实际问题的一般思路
把立体图形中的线路问题转化为平面上的路线问题,然后再平面上两点间线段最短的原理利用勾股定理求解。
将实际问题转化为数学模型,然后利用勾股定理求解。
肆
课后作业
基础题:1. 习题1.4第1题。
提高题:2. 习题1.4第2题。
谢
谢
第一章 勾股定理
问题解决策略:反思
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
看图片,引出问题:有一块长方形绿地,绿地周边是小路,在绿地旁边的B处有健身器材.居住在A处的居民在看到牌子上“禁止踩踏花草,文明步行”后,为了走近路而不惜践踏草地直接从A到B.各位同学,你知道他们为什么不走绿地周边的路吗?
新知初探
贰
新知初探
探究一:路径最短问题
贰
A
B
问题:如图,有一个圆柱,它的高等于12cm,底面圆的周长为18cm,在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?
新知初探
贰
新知初探
贰
活动1 理解问题
(1)在这个问题中,已知条件有哪些?你认为已知条件足够解决这个问题吗?
(2)沿侧面爬行的可能路线有哪些?什么情况下路线最短?请你用图形水杯等物品实际感受一下。
新知初探
贰
自己做一个圆柱,尝试从点A到点B沿圆柱侧面画几条路线,你觉得哪条路线最短?
A
B
A
B
A
B
方案①
方案②
方案③
新知初探
贰
活动2 拟定计划
(1)以前研究过最短路线问题吗?这个问题与以前研究的最短路线问题有什么不同?
(2)如何将曲面最短路线问题转化为平面上的最短路线问题?各个点的位置如何确定?
新知初探
贰
如图,将圆柱侧面剪开展成一个长方形,点A到点B的最短路线是什么?你画对了吗?
A
B
A
B
A
B
因为两点之间线段最短,
所以方案③的路线最短.
新知初探
贰
活动3 实施计划
(1)如图,将圆柱侧面剪开,确定展开图的形状,以及与圆柱的对应关系。
(3)在图中确定A,B两点之间最短的路线,并计算它的长度。
(2)在图中标出点B的位置。
新知初探
贰
蚂蚁从点A出发,想吃到B点上的食物,它沿圆柱侧面爬行的最短路程是多少?
在Rt△ABC中,
AC=12cm,BC=18÷2=9(cm).
由勾股定理,得
AB2=AC2+BC2
=122+92
=225.
所以最短路程AB=15cm.
A
B
C
高12cm,底面周长18cm.
新知初探
贰
活动4 回顾反思
(1)在拟订解决问题的方案和实施方案的过程中,你获得了哪些经验 与同伴进行交流。
(2)从这个问题中,影响结果的量有哪些 如果改变有关的量,你还能求解吗?例如,改变圆柱的形状,改变A,B两点的位置,改为沿着圆柱表面爬……这时又会有哪些新的问题 选择部分问题进行研究,并与同伴进行交流。
新知初探
贰
(4)生活中还有哪些现实问题涉及几何体表面上的最短距离 举几个实例,并思考解决问题的方案。
(5)对于解决问题之后的回顾反思,你有哪些体会 与同伴进行交流。
(3)解决这个问题的经验,还可以运用到哪些问题中 例如,能否解决正方体、长方体等几何体表面两点之间的最短距离问题
新知初探
贰
活动5 变式训练
如图,一只蜘蛛在一个长方体木块
的顶点A处,一只苍蝇在这个长方体
木块的顶点G处,若AB=3 cm,BC=5 cm,
BF=6 cm,问蜘蛛要沿着怎样的路线爬
行,才能最快抓到苍蝇?这时蜘蛛走
过的路程是多少?
新知初探
贰
解:如图,根据题意,得A点到G点的路线有以上三种情况:
AG2=AF2+GF2=92+52=106
AG2=AB2+BG2=32+112=130
AG2=AC2+CG2=82+62=100。
综上,蜘蛛走过的路程是10 cm。
新知初探
贰
解决问题之后的反思,一般可以关注以下几个方面,反思解决问题的过程,强化解决问题的经验,比较解决问题的方法,形成多样的解决问题的方法,思考方法的本质,促进方法的运用,改变问题的条件,研究更多的问题。
活动6 小结
当堂达标
叁
当堂达标
叁
1.如图,已知圆柱的底面周长为10cm,高AB为12cm,BC是底面的直径,一只蚂蚁沿着圆柱侧面爬行觅食从点C爬到点A,则蚂蚁爬行的最短路线为 cm.
13
叁
当堂达标
叁
2.如图,一个三级台阶,它的每一级的长、宽和高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的点,A点处有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶爬到B点,至少需爬( )
A.13 cm B.40 cm
C.130 cm D.169 cm
C
叁
当堂达标
叁
3.如图,长方体的透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深为AE=40 cm,在水面上紧贴内壁G处有一鱼铒,G在水面线EF上,且EG=60 cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内到G处吃鱼铒,则小虫爬行的最短路线长为( )
A.40 cm B.60 cm
C.80 cm D.100 cm
D
叁
课堂小结
肆
课堂小结
肆
勾股定理的应用
解决图形中路线最短的问题关键
应用勾股定理解决实际问题的一般思路
把立体图形中的线路问题转化为平面上的路线问题,然后再平面上两点间线段最短的原理利用勾股定理求解。
将实际问题转化为数学模型,然后利用勾股定理求解。
肆
课后作业
基础题:1. 习题1.4第1题。
提高题:2. 习题1.4第2题。
谢
谢
同课章节目录
