5.1任意角和弧度制 同步练习(含答案)
文档属性
| 名称 | 5.1任意角和弧度制 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 345.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-05 17:40:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.1任意角和弧度制
一、单选题
1.(2016高一下·新乡期末)若2弧度的圆心角所夹的扇形的面积是4cm2,则该圆心角所对的弧长为( )
A.2πcm B.2cm C.4πcm D.4cm
2.(2024高一上·河北月考)体操中有“前空翻转体540度”这样的动作名称,则化成弧度是( )
A. B. C. D.
3.若某个扇形的半径为3cm,弧长为πcm,则该扇形的面积为( )
A.πcm2 B. cm2 C.3πcm2 D.6πcm2
4.(2023·河北会考)若圆锥的底面半径为3,体积为,则此圆锥的侧面展开图的圆心角是( )
A. B. C. D.
5.(2020高二下·应城期中)如图,以棱长为2的正方体的顶点A为球心,以 为半径做一个球面,则该正方体的表面被球面所截得的所有弧长之和为( ).
A. B. C. D.
6.(2022高一上·绍兴期末)在平面直角坐标系xOy中,以原点O为圆心的单位圆与锐角x的终边交于点P,过点作x轴的垂线与锐角x的终边交于点T,如图所示,的面积小于扇形AOP的面积,扇形AOP的面积小于的面积,则( )
A.,
B.,
C.,
D.,
7.(2024高二下·镇海区期末)已知正方体的棱长为3,以为球心,为半径的球面与正方体表面的交线记为曲线,则曲线的长度为( )
A. B. C. D.
二、多选题
8.(2024高一上·相城月考)下列结论正确的有( )
A.已知,则
B.已知扇形的弧长为,面积为,则该弧所对弦长为
C.已知,则3
D.若函数的值域为,则实数的范围是
9.(2025高三下·张掖月考)设曲线C的方程为x2+y2=2|x|-2|y|,则( )
A.曲线C既是轴对称图形,又是中心对称图形
B.曲线C围成图形的面积为
C.曲线C的周长为
D.曲线上任意两点间距离的最大值为4
三、填空题
10.(2024高一上·天津市月考)已知扇形的圆心角为rad,其周长是cm,则该扇形的面积是
11.(2025高一下·宝山月考)已知某扇形的圆心角为,半径为,则该扇形的面积为 .
12.(2016高一上·黄冈期末)若角α和β的终边关于直线x+y=0对称,且α=﹣ ,则角β的集合是
13.(2024高一下·丰城月考)如图所示,终边落在阴影部分(包括边界)的角的集合为 .
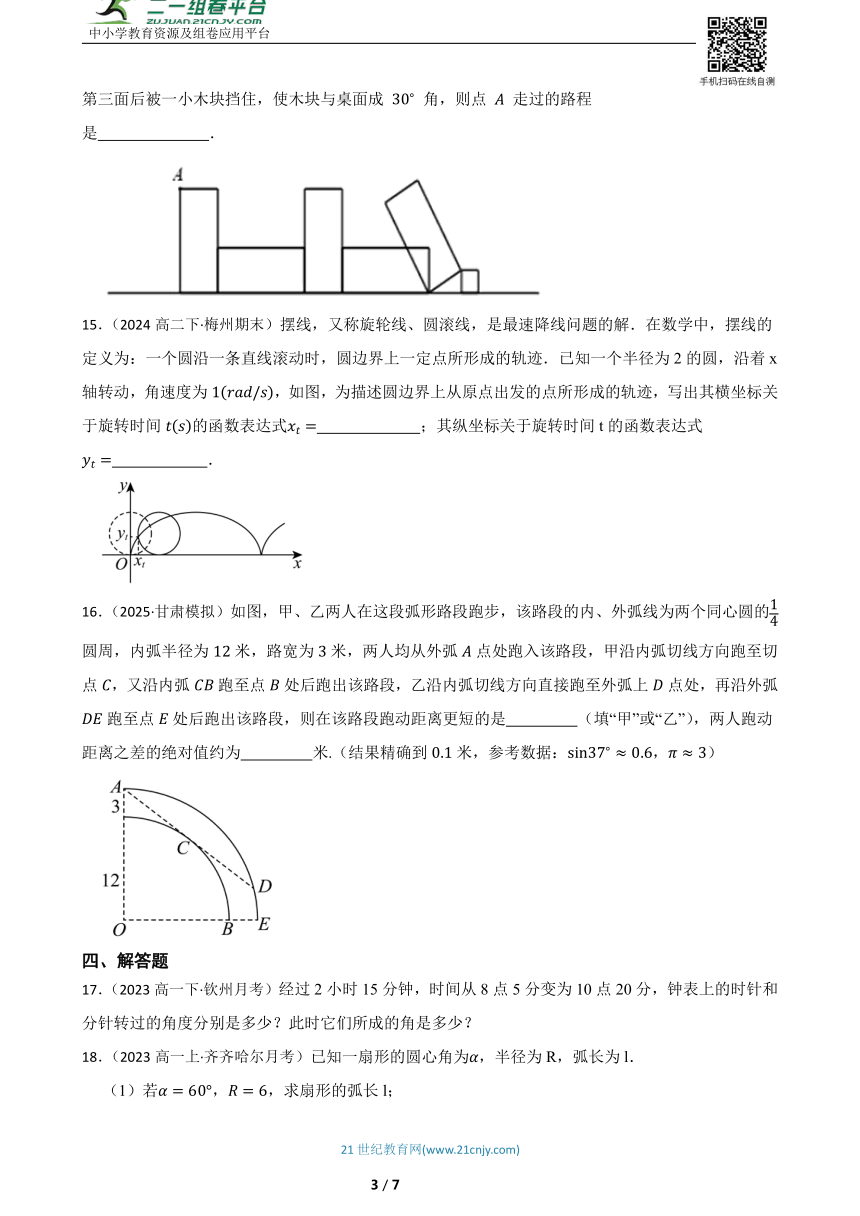
14.(2019高一下·上海月考)如图,长为 ,宽为 的矩形木块,在桌面上作无滑动翻滚,翻滚到第三面后被一小木块挡住,使木块与桌面成 角,则点 走过的路程是 .
15.(2024高二下·梅州期末)摆线,又称旋轮线、圆滚线,是最速降线问题的解.在数学中,摆线的定义为:一个圆沿一条直线滚动时,圆边界上一定点所形成的轨迹.已知一个半径为2的圆,沿着x轴转动,角速度为,如图,为描述圆边界上从原点出发的点所形成的轨迹,写出其横坐标关于旋转时间的函数表达式 ;其纵坐标关于旋转时间t的函数表达式 .
16.(2025·甘肃模拟)如图,甲、乙两人在这段弧形路段跑步,该路段的内、外弧线为两个同心圆的圆周,内弧半径为米,路宽为米,两人均从外弧点处跑入该路段,甲沿内弧切线方向跑至切点,又沿内弧跑至点处后跑出该路段,乙沿内弧切线方向直接跑至外弧上点处,再沿外弧跑至点处后跑出该路段,则在该路段跑动距离更短的是 (填“甲”或“乙”),两人跑动距离之差的绝对值约为 米.(结果精确到米,参考数据:,)
四、解答题
17.(2023高一下·钦州月考)经过2小时15分钟,时间从8点5分变为10点20分,钟表上的时针和分针转过的角度分别是多少?此时它们所成的角是多少?
18.(2023高一上·齐齐哈尔月考)已知一扇形的圆心角为,半径为R,弧长为l.
(1)若,,求扇形的弧长l;
(2)若扇形面积为16,求扇形周长的最小值,及此时扇形的圆心角.
19.(2024高一下·遵义月考)玉雕在我国历史悠久,拥有深厚的文化底蕴,数千年来始终以其独特的内涵与魅力深深吸引着世人.如图1,这是一幅扇形玉雕壁画,其平面图为图2所示的扇形环面(由扇形OCD挖去扇形OAB后构成).已知该扇形玉雕壁画的周长为320厘米.
(1)若厘米.求该扇形玉雕壁画的曲边的长度;
(2)若.求该扇形玉雕壁画的扇面面积的最大值.
20.将下列各角由弧度转换为角度:
答案解析部分
1.【答案】D
【知识点】扇形的弧长与面积
2.【答案】B
【知识点】弧度制、角度制及其之间的换算
3.【答案】B
【知识点】扇形的弧长与面积
4.【答案】D
【知识点】扇形的弧长与面积
5.【答案】D
【知识点】扇形的弧长与面积
6.【答案】D
【知识点】全称量词命题;存在量词命题;扇形的弧长与面积
7.【答案】B
【知识点】扇形的弧长与面积
8.【答案】B,C
【知识点】对数的性质与运算法则;换底公式及其推论;扇形的弧长与面积
9.【答案】A,B,D
【知识点】扇形的弧长与面积
10.【答案】
【知识点】扇形的弧长与面积
11.【答案】
【知识点】扇形的弧长与面积
12.【答案】{β|β=2kπ﹣ ,k∈Z}
【知识点】象限角、轴线角;终边相同的角
13.【答案】
【知识点】终边相同的角
14.【答案】
【知识点】扇形的弧长与面积
15.【答案】;
【知识点】扇形的弧长与面积
16.【答案】甲;
【知识点】扇形的弧长与面积
17.【答案】解:时针每小时转过=-30°,则每分钟转过=-0.5°,
而分针每分钟转过=-6°,故经过2小时15分钟后,
时针转过(2×60+15)×(-0.5°)=﹣67.5°,
分针转过(2×60+15)×(-6°)=﹣810°.
2小时15分钟后为10点20分,此时分针指向4,时针则由指向10转过了20×(﹣0.5°)=-10°,
此时时针和分针所成的角为180°-10°=170°.
【知识点】任意角
18.【答案】(1)解:因为,,
所以扇形的弧长;
(2)解:由扇形面积,得,
则扇形周长为,
当且仅当,即时,取等号,
此时,,所以,
所以扇形周长的最小值为,此时.
【知识点】基本不等式在最值问题中的应用;弧度制、角度制及其之间的换算;扇形的弧长与面积
19.【答案】(1)设弧的长度为厘米,弧的长度为厘米.
因为,所以,所以.
因为厘米,所以厘米.
因为该扇形玉雕壁画的周长为320厘米,所以,
所以,解得,即弧的长度为160厘米.
(2)因为,所以,所以,
则扇形的面积,扇形的面积,
故该扇形玉雕壁画的扇面面积.
因为该扇形玉雕壁画的周长为320厘米,所以
所以,
则,从而,当且仅当时,等号成立,
故,即该扇形玉雕壁画的扇面面积的最大值为6400平方厘米.
【知识点】基本不等式;扇形的弧长与面积
20.【答案】解:=×==480°;
【知识点】弧度制、角度制及其之间的换算
21世纪教育网(www.21cnjy.com)
2 / 7
5.1任意角和弧度制
一、单选题
1.(2016高一下·新乡期末)若2弧度的圆心角所夹的扇形的面积是4cm2,则该圆心角所对的弧长为( )
A.2πcm B.2cm C.4πcm D.4cm
2.(2024高一上·河北月考)体操中有“前空翻转体540度”这样的动作名称,则化成弧度是( )
A. B. C. D.
3.若某个扇形的半径为3cm,弧长为πcm,则该扇形的面积为( )
A.πcm2 B. cm2 C.3πcm2 D.6πcm2
4.(2023·河北会考)若圆锥的底面半径为3,体积为,则此圆锥的侧面展开图的圆心角是( )
A. B. C. D.
5.(2020高二下·应城期中)如图,以棱长为2的正方体的顶点A为球心,以 为半径做一个球面,则该正方体的表面被球面所截得的所有弧长之和为( ).
A. B. C. D.
6.(2022高一上·绍兴期末)在平面直角坐标系xOy中,以原点O为圆心的单位圆与锐角x的终边交于点P,过点作x轴的垂线与锐角x的终边交于点T,如图所示,的面积小于扇形AOP的面积,扇形AOP的面积小于的面积,则( )
A.,
B.,
C.,
D.,
7.(2024高二下·镇海区期末)已知正方体的棱长为3,以为球心,为半径的球面与正方体表面的交线记为曲线,则曲线的长度为( )
A. B. C. D.
二、多选题
8.(2024高一上·相城月考)下列结论正确的有( )
A.已知,则
B.已知扇形的弧长为,面积为,则该弧所对弦长为
C.已知,则3
D.若函数的值域为,则实数的范围是
9.(2025高三下·张掖月考)设曲线C的方程为x2+y2=2|x|-2|y|,则( )
A.曲线C既是轴对称图形,又是中心对称图形
B.曲线C围成图形的面积为
C.曲线C的周长为
D.曲线上任意两点间距离的最大值为4
三、填空题
10.(2024高一上·天津市月考)已知扇形的圆心角为rad,其周长是cm,则该扇形的面积是
11.(2025高一下·宝山月考)已知某扇形的圆心角为,半径为,则该扇形的面积为 .
12.(2016高一上·黄冈期末)若角α和β的终边关于直线x+y=0对称,且α=﹣ ,则角β的集合是
13.(2024高一下·丰城月考)如图所示,终边落在阴影部分(包括边界)的角的集合为 .
14.(2019高一下·上海月考)如图,长为 ,宽为 的矩形木块,在桌面上作无滑动翻滚,翻滚到第三面后被一小木块挡住,使木块与桌面成 角,则点 走过的路程是 .
15.(2024高二下·梅州期末)摆线,又称旋轮线、圆滚线,是最速降线问题的解.在数学中,摆线的定义为:一个圆沿一条直线滚动时,圆边界上一定点所形成的轨迹.已知一个半径为2的圆,沿着x轴转动,角速度为,如图,为描述圆边界上从原点出发的点所形成的轨迹,写出其横坐标关于旋转时间的函数表达式 ;其纵坐标关于旋转时间t的函数表达式 .
16.(2025·甘肃模拟)如图,甲、乙两人在这段弧形路段跑步,该路段的内、外弧线为两个同心圆的圆周,内弧半径为米,路宽为米,两人均从外弧点处跑入该路段,甲沿内弧切线方向跑至切点,又沿内弧跑至点处后跑出该路段,乙沿内弧切线方向直接跑至外弧上点处,再沿外弧跑至点处后跑出该路段,则在该路段跑动距离更短的是 (填“甲”或“乙”),两人跑动距离之差的绝对值约为 米.(结果精确到米,参考数据:,)
四、解答题
17.(2023高一下·钦州月考)经过2小时15分钟,时间从8点5分变为10点20分,钟表上的时针和分针转过的角度分别是多少?此时它们所成的角是多少?
18.(2023高一上·齐齐哈尔月考)已知一扇形的圆心角为,半径为R,弧长为l.
(1)若,,求扇形的弧长l;
(2)若扇形面积为16,求扇形周长的最小值,及此时扇形的圆心角.
19.(2024高一下·遵义月考)玉雕在我国历史悠久,拥有深厚的文化底蕴,数千年来始终以其独特的内涵与魅力深深吸引着世人.如图1,这是一幅扇形玉雕壁画,其平面图为图2所示的扇形环面(由扇形OCD挖去扇形OAB后构成).已知该扇形玉雕壁画的周长为320厘米.
(1)若厘米.求该扇形玉雕壁画的曲边的长度;
(2)若.求该扇形玉雕壁画的扇面面积的最大值.
20.将下列各角由弧度转换为角度:
答案解析部分
1.【答案】D
【知识点】扇形的弧长与面积
2.【答案】B
【知识点】弧度制、角度制及其之间的换算
3.【答案】B
【知识点】扇形的弧长与面积
4.【答案】D
【知识点】扇形的弧长与面积
5.【答案】D
【知识点】扇形的弧长与面积
6.【答案】D
【知识点】全称量词命题;存在量词命题;扇形的弧长与面积
7.【答案】B
【知识点】扇形的弧长与面积
8.【答案】B,C
【知识点】对数的性质与运算法则;换底公式及其推论;扇形的弧长与面积
9.【答案】A,B,D
【知识点】扇形的弧长与面积
10.【答案】
【知识点】扇形的弧长与面积
11.【答案】
【知识点】扇形的弧长与面积
12.【答案】{β|β=2kπ﹣ ,k∈Z}
【知识点】象限角、轴线角;终边相同的角
13.【答案】
【知识点】终边相同的角
14.【答案】
【知识点】扇形的弧长与面积
15.【答案】;
【知识点】扇形的弧长与面积
16.【答案】甲;
【知识点】扇形的弧长与面积
17.【答案】解:时针每小时转过=-30°,则每分钟转过=-0.5°,
而分针每分钟转过=-6°,故经过2小时15分钟后,
时针转过(2×60+15)×(-0.5°)=﹣67.5°,
分针转过(2×60+15)×(-6°)=﹣810°.
2小时15分钟后为10点20分,此时分针指向4,时针则由指向10转过了20×(﹣0.5°)=-10°,
此时时针和分针所成的角为180°-10°=170°.
【知识点】任意角
18.【答案】(1)解:因为,,
所以扇形的弧长;
(2)解:由扇形面积,得,
则扇形周长为,
当且仅当,即时,取等号,
此时,,所以,
所以扇形周长的最小值为,此时.
【知识点】基本不等式在最值问题中的应用;弧度制、角度制及其之间的换算;扇形的弧长与面积
19.【答案】(1)设弧的长度为厘米,弧的长度为厘米.
因为,所以,所以.
因为厘米,所以厘米.
因为该扇形玉雕壁画的周长为320厘米,所以,
所以,解得,即弧的长度为160厘米.
(2)因为,所以,所以,
则扇形的面积,扇形的面积,
故该扇形玉雕壁画的扇面面积.
因为该扇形玉雕壁画的周长为320厘米,所以
所以,
则,从而,当且仅当时,等号成立,
故,即该扇形玉雕壁画的扇面面积的最大值为6400平方厘米.
【知识点】基本不等式;扇形的弧长与面积
20.【答案】解:=×==480°;
【知识点】弧度制、角度制及其之间的换算
21世纪教育网(www.21cnjy.com)
2 / 7
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
