6.1 第3课时 方差 课件(共18张PPT) 2025-2026学年数学北师大版(2024)八年级上册
文档属性
| 名称 | 6.1 第3课时 方差 课件(共18张PPT) 2025-2026学年数学北师大版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-03 23:36:17 | ||
图片预览






文档简介
(共18张PPT)
第3课时 方差
第六章 数据的分析
1.平均数与方差
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
小优和小翼的最近 5 次数学成绩如下:
波动较小
小优:90,88,90,93,90
小翼:70,80,90,80,100
对于二人的分数,你觉得各有什么特点?
小优成绩非常稳定,小翼近来进步很大.
如何理解非常稳定?
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:方差
贰
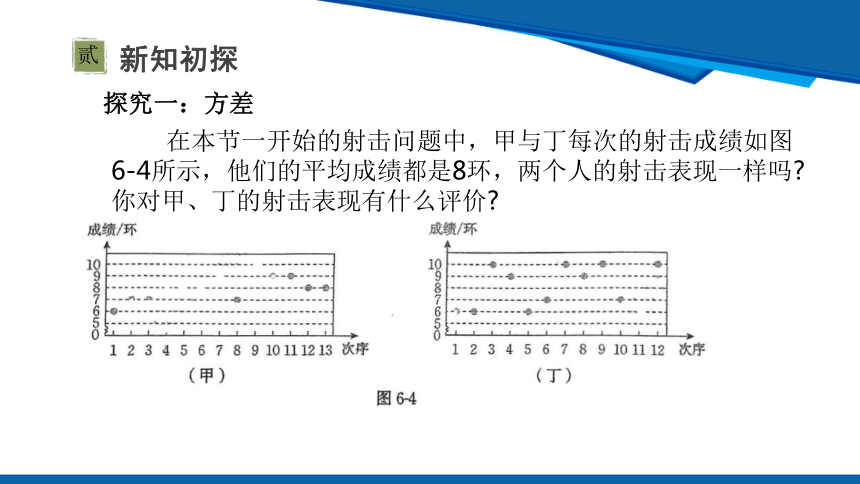
在本节一开始的射击问题中,甲与丁每次的射击成绩如图 6-4所示,他们的平均成绩都是8环,两个人的射击表现一样吗 你对甲、丁的射击表现有什么评价
新知初探
贰
(1)你觉得谁发挥得更稳定 你的理由是什么
(2)你能设法通过计算说明两人成绩的稳定程度吗 与同伴进行交流。
新知初探
贰
归纳总结
现实生活中,除了关心数据的“平均水平”外,人们还关注数据的离散程度,即它们相对于平均水平的偏离情况.
在统计学里,数据的离散程度可以用离差平方和、方差
或标准差等统计量来刻画
离差平方和是各个数据与它们平均数之差的平方和 ,即
新知初探
贰
方差和标准差
方差是各个数据与平均数之差的平方的平均数,
即
一般而言,一组数据的方差或标准差越小,这组数据就越稳定.
其中, 是 x1,x2,…,xn 的平均数,s2 是方差,而标准差就是方差的算术平方根.
新知初探
探究二:典例精析
贰
例2 计算图6-4中甲射击成绩的标准差(结果精确到0.01环).
解:
环
(环)。
所以 ,甲射击成绩的标准差约为1.04环。
新知初探
贰
(1)计算图6-1中丙射击成绩的方差,并对甲、丙的射击成绩进行比较。
思考交流
(2)丁又进行了几次射击,这时,他所有射击成绩的平均数没变,但方差变小了。你认为丁后面几次射击的成绩有什么特点 与同伴进行交流。
新知初探
贰
随堂练习
1.某组数据为2, 4, 6, 8,其方差为______。
2.某组数据为1, 3, 5, 7, 9,这组数据的方差为 。
3.某组数据的平均数为15,方差为25,请计算这组数据的标准差,
并分析数据的离散程度。
5
8
解:标准差为5,说明数据点与平均数的平均距离为5,数据
的离散程度较大。
当堂达标
叁
当堂达标
叁
1. 人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差如下: , , ,则成绩较为稳定的班级是 ( )
A. 甲班 B. 乙班 C. 两班成绩一样稳定 D. 无法确定
B
2. 数据-2,-1,0,1,2 的方差是___,标准差是____.
3. 五个数 1,3,a,5,8 的平均数是 4,则 a =_____,这五个数的方差为_____.
2
3
5.6
叁
肆
叁
叁
当堂达标
叁
4. 比较下列两组数据的方差:
A 组:0,10,5,5,5,5,5,5,5,5;
B 组:4,6,3,7,2,8,1,9,5,5.
解:
所以 A 组数据的方差小于 B 组数据的方差.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
数据的离散程度
离差平方和
方差
标准差
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第17题
谢
谢
第3课时 方差
第六章 数据的分析
1.平均数与方差
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
小优和小翼的最近 5 次数学成绩如下:
波动较小
小优:90,88,90,93,90
小翼:70,80,90,80,100
对于二人的分数,你觉得各有什么特点?
小优成绩非常稳定,小翼近来进步很大.
如何理解非常稳定?
叁
肆
叁
壹
新知初探
贰
新知初探
探究一:方差
贰
在本节一开始的射击问题中,甲与丁每次的射击成绩如图 6-4所示,他们的平均成绩都是8环,两个人的射击表现一样吗 你对甲、丁的射击表现有什么评价
新知初探
贰
(1)你觉得谁发挥得更稳定 你的理由是什么
(2)你能设法通过计算说明两人成绩的稳定程度吗 与同伴进行交流。
新知初探
贰
归纳总结
现实生活中,除了关心数据的“平均水平”外,人们还关注数据的离散程度,即它们相对于平均水平的偏离情况.
在统计学里,数据的离散程度可以用离差平方和、方差
或标准差等统计量来刻画
离差平方和是各个数据与它们平均数之差的平方和 ,即
新知初探
贰
方差和标准差
方差是各个数据与平均数之差的平方的平均数,
即
一般而言,一组数据的方差或标准差越小,这组数据就越稳定.
其中, 是 x1,x2,…,xn 的平均数,s2 是方差,而标准差就是方差的算术平方根.
新知初探
探究二:典例精析
贰
例2 计算图6-4中甲射击成绩的标准差(结果精确到0.01环).
解:
环
(环)。
所以 ,甲射击成绩的标准差约为1.04环。
新知初探
贰
(1)计算图6-1中丙射击成绩的方差,并对甲、丙的射击成绩进行比较。
思考交流
(2)丁又进行了几次射击,这时,他所有射击成绩的平均数没变,但方差变小了。你认为丁后面几次射击的成绩有什么特点 与同伴进行交流。
新知初探
贰
随堂练习
1.某组数据为2, 4, 6, 8,其方差为______。
2.某组数据为1, 3, 5, 7, 9,这组数据的方差为 。
3.某组数据的平均数为15,方差为25,请计算这组数据的标准差,
并分析数据的离散程度。
5
8
解:标准差为5,说明数据点与平均数的平均距离为5,数据
的离散程度较大。
当堂达标
叁
当堂达标
叁
1. 人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差如下: , , ,则成绩较为稳定的班级是 ( )
A. 甲班 B. 乙班 C. 两班成绩一样稳定 D. 无法确定
B
2. 数据-2,-1,0,1,2 的方差是___,标准差是____.
3. 五个数 1,3,a,5,8 的平均数是 4,则 a =_____,这五个数的方差为_____.
2
3
5.6
叁
肆
叁
叁
当堂达标
叁
4. 比较下列两组数据的方差:
A 组:0,10,5,5,5,5,5,5,5,5;
B 组:4,6,3,7,2,8,1,9,5,5.
解:
所以 A 组数据的方差小于 B 组数据的方差.
叁
肆
叁
叁
课堂小结
肆
课堂小结
肆
数据的离散程度
离差平方和
方差
标准差
叁
肆
叁
肆
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第17题
谢
谢
同课章节目录
